快车道ASS框架中的Gas效率与MEV权衡 - 深入探讨特定领域区块链的限制

WIP - 工作进行中

简介

在本技术博客中，我们将深入探讨Gas效率的权衡，利用Fastlane的ASS框架^1中的见解。它们的观察，特别是围绕特定领域的约束，将作为开发出一个严谨的数学模型的基础，该模型捕捉不同区块链领域（例如，Solana、Ethereum、Monad 等）中Gas效率的复杂性。我们将把线性权衡扩展到多维空间，使用正式的数学符号并通过二维图形可视化这种权衡。

理解可组合性、MEV 捕获和Gas效率等关键因素之间的权衡对优化区块链架构至关重要。Fastlane的ASS框架提供了可视化这些权衡的初步方法。然而，简化模型往往忽视了特定领域的因素，尤其是与Gas效率相关的，不同区块链系统施加了独特的约束和机会。

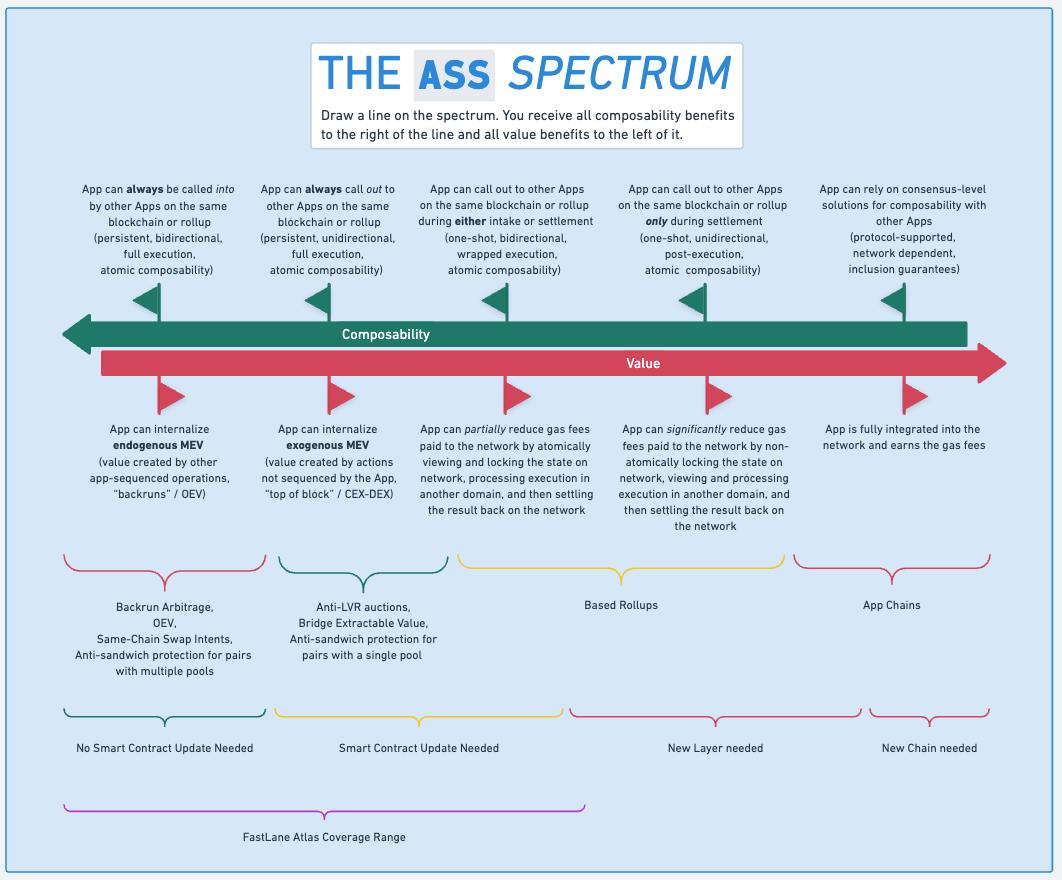
图：Fastlane的ASS框架，来源：Fastlane^1

概述 - 区块链架构中的Gas效率权衡

在任何区块链系统中，Gas效率反映了执行交易所需的计算资源成本。优化Gas效率对可扩展性、用户体验和长期可行性至关重要。然而，提高Gas效率通常伴随着权衡，尤其是在MEV（最大可提取价值）捕获和可组合性方面。

ASS框架提供了一个简化的视图，但非常实用，建议Gas效率和价值提取之间存在线性权衡。但是，正如Fastlane的首席执行官兼创始人 Alex Watts 指出^1，特定领域的约束在塑造这些权衡中起着重要作用。像Solana这样的系统，通过其访问列表实现细粒度的状态锁定，允许在不牺牲过多可组合性或MEV捕获的情况下提高Gas效率。反之，像Monad等其他区块链缺乏这样的机制，导致在优化可组合性或价值提取时，Gas效率急剧下降。

我们在本文中的目标是通过数学模型形式化这一权衡，定义Gas效率如何在特定领域中依赖于可组合性、MEV捕获和其他变量。让我们从关键变量定义和特定领域的函数开始，建立一个坚实的基础。

定义和符号

• $C$: 可组合性——去中心化应用程序（dApps）无缝交互的能力。$C \in [0, 1]$，其中0表示没有可组合性，1表示完全的原子可组合性。
• $M$: MEV 捕获——一个系统捕获内生和外生 MEV 的程度。$M \in [0, 1]$，其中0表示没有 MEV 捕获，1表示全部 MEV 捕获。
• $G_d$: Gas效率——特定领域 $d$ 中Gas使用的效率。$G_d \in [0, 1]$，其中1表示最大Gas效率。
• $S$: 安全性——系统抵御诸如前置运行或再入攻击的能力。$S \in [0, 1]$，其中1表示完全安全。
• $L$: 延迟——交易确定所需时间。值越低表示最终确定时间越快。

特定领域的Gas效率函数

由于Gas效率在不同区块链之间有所不同，我们将其定义为特定领域函数 $G_d$，其中 $d$ 表示区块链（例如，Solana、Monad、Ethereum 等）：

$$G_d = f_d(C, M, S, L)$$

函数 $f_d$ 取决于相关区块链的具体特性。例如，Solana 的访问列表使Gas使用优化得以改善，而 Monad 缺乏此类特性，从而导致不同的权衡。

让我们更详细地查看这个Gas效率函数在每个领域是如何工作的。

Solana

在 Solana 中，通过访问列表对状态锁定的细粒度控制，允许在验证过程中无需状态访问或执行即可实现更好的Gas效率。我们可以将Solana的Gas效率建模为：

$$G_{\text{Solana}} = C^\alpha \cdot M^\beta \cdot S^\gamma \cdot L^\delta \quad \text{其中 } \alpha, \beta, \gamma, \delta > 0$$

在这种情况下：

• $\alpha$: 可组合性对Gas效率的影响。Solana能够更好地处理可组合性，即使在 $C$ 很大时也能保持高Gas效率。
• $\beta$: 表示MEV捕获和Gas效率之间的权衡。Solana的架构在这方面比大多数区块链更好地缓解了这一权衡。
• $\gamma$ 和 $\delta$: 安全性和延迟对Gas效率的影响。这些参数取决于系统对交易确认和安全要求的敏感程度。

Monad

对于Monad，缺乏这样的优化，Gas效率权衡对MEV捕获和可组合性的变化更加敏感。我们引入一个惩罚项，以考虑Monad在处理MEV方面的局限性：

$$G_{\text{Monad}} = C^\alpha \cdot M^\beta \cdot S^\gamma \cdot L^\delta \cdot h(M)$$

在这里，$h(M)$ 是一个惩罚函数，随着MEV捕获的增加而增长，反映了系统试图捕获更多 MEV 时对Gas效率的更高成本。这个项惩罚系统缺乏可组合性优化，反映出更陡峭的权衡曲线。

参考文献

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～