针对ZK友好哈希函数的代数攻击

引言

在我们上一个帖子中，我们讨论了各种 ZK 友好哈希函数的设计原理和性能。这些包括 MiMC、Poseidon、Vision 和 Rescue。尽管这些结构可能略有不同，但其基本概念是相同的：将电路表示为大域中的简单表达式，这使得证明效率在证明者执行时间和证明大小方面都是高效的。然而，问题依然存在：它们真的足够安全，可以托管数十亿美元吗？让我们深入研究那些对 ZK 友好哈希函数特别有效的攻击。

ZK 友好哈希函数

从高层角度来看，ZK 友好的哈希函数是使用代数上简单的密钥置换构造的，称为 arithmetization-oriented ciphers (AOCs)。AOCs 基于 SPN↗ 或 Feistel↗ 网络。然后，这些置换通过海绵框架转化为哈希函数。

（此外，最近提出了一些新的置换，例如这一篇↗ 和这一篇↗。这两篇论文被接受到 2023 年 CRYPTO。我们建议查看这些论文，因为它们提供了显著的性能优势。）

由于密钥置换结构是经过多轮线性和非线性操作构成的，加密轮数越高，哈希函数越安全，但性能会下降。设计者必须考虑每种可能的攻击，并确定减轻这些攻击所需的最低轮数界限。

成熟需要时间，包括 AOCs

不幸的是，尽管设计者仔细考虑每一种可能的攻击，甚至添加安全边际，但这并不是证明结构安全的强有力证据。正如我们将在本帖中展示的示例，即使设计者已经尽力而为，仍然可能存在设计者未考虑的新攻击。即便是在顶级会议上发表的同行评审论文也可能存在被攻击的风险。例如，针对同态加密的一个密码名为 Chaghri↗，在 ACM CCS 2022 中发表，但在其发表后仅三个月就发现了一个攻击↗。

新原语通常在足够的时间过后被业界接受。这与原论文中的声明无关，而是基于足够多的人分析它们，以确定它们已经成熟到可以实际使用的程度。

从设计者的角度来看，考虑多种攻击，包括我们将讨论的和正在发展的攻击，以创建稳健的安全设计是重要的。

在这篇文章中，我们将讨论特别有效、应当被考虑的对 ZK 友好哈希函数的代数攻击，包括对实际提出的原语的攻击。虽然理解本文不需要广泛的 ZK 知识，但如果你是 ZK 初学者，可以查看我们最新关于 ZK 的博文帖子。

代数攻击

在开始引入代数攻击之前，我们应该澄清攻击的目标。哈希函数的基本安全属性包括预像抗性、第二预像抗性和碰撞抗性。因此，攻击者的主要目标是恢复预像或找到碰撞对。然而，从设计者的角度来看，难以说服别人他们的哈希函数满足安全属性。

同时，ZK 哈希函数通常基于块密码。一旦密钥固定，块密码就变成了一个置换，这些置换通过海绵框架被转化为哈希函数。数学上证明，来源于海绵构造的哈希函数是安全的，如果置换是安全的。因此，设计者并不是直接展示哈希函数的安全性，而是展示用于海绵构造的块密码的安全性。相反，攻击者则希望证明块密码不安全。例如，如果攻击者能够在测试所有可能的密钥候选项之前，根据明文-密文对 $(P_i, C_i)$ 更快地恢复密钥 $K$，则称为密钥恢复攻击。如果块密码不安全，则削弱了设计者对由块密码创建的哈希函数是安全的主张。

ZK 友好的哈希函数通过在大域中以简单表达式表示。在传统的密码设计中，统计攻击被认为是最强的攻击，称为 差分↗ 和 线性↗ 密码分析。然而，当场大时，即使轮数很少，这些攻击也不适用。另一方面，针对低算术复杂度的攻击是有效的。

插值(Interpolation)攻击

插值攻击是一种在不知道密钥的情况下构造对应于加密函数的多项式的攻击。设 $E_k : \mathbb F_q \rightarrow \mathbb F_q$为一个加密函数。对于一个固定密钥 $k$，可以使用拉格朗日插值构造多项式 $E_k(x)$，例如，当我们考虑 MiMC 的两轮时，$E_k(x) = ((x+k)^3 + k + c_1)^3 + k$。对于 $x$ 来说，这是一个次数为 $9$ 的多项式。

一旦攻击者构造了多项式 $E_k(x)$，就可以获得任何明文的密文，这与知道密钥是等效的。此外，攻击者可能能够从 $E_k(x)$ 中提取密钥 $k$，因为 $x^8$ 的系数为 $9k$。

当一个多项式的次数为 $d$ 时，构造拉格朗日插值多项式的复杂度为$O(d\log d)$。因此，用于表示加密函数的多项式的次数应该足够高。例如，在 MiMC 中，轮数 $r$ 确定为 $r = \lceil \log_3 q \rceil$，以确保次数 $d$ 达到 $q-1$ 的最大值。

插值攻击针对的是明文的单变量方程。如果明文是 $\mathbb F_q^m$而不是 $\mathbb F_q$，则无法直接应用此攻击。

GCD 攻击

GCD 攻击是一种密钥恢复攻击，涉及计算 GCD。在 GCD 攻击中，变量是密钥 $K$。我们将加密函数表示为 E(K,x)E(K, x)E(K,x)。对于明文-密文对 $(x, y)$，我们有 $E(K, x) - y = 0$，当 $K = k$。现在，让我们考虑从两个对 $(x_1, y_1)$和 $(x_2, y_2)$ 导出的两个多项式。$E(K, x_1) - y_1$ 和 $E(K, x_2) - y_2$ 有一个公共因子$(K-k)$，因为 $E(k, x_1) - y_1 = E(k, x_2) - y_2 = 0$。（$K$ 表示密钥的变量，而 $k$ 是密钥的实际值。）通过计算 GCD 可以确定这个公共因子。

对于一个次数为 $d$ 的两个多项式，查找 GCD 的复杂度为 $O(d\log^2d)$。因此，保持最高程度也对抗此攻击是有益的。幸运的是，随着轮数的增加，次数呈指数增长，因此设计师可以较容易地构建防御以抵御插值攻击和 GCD 攻击。

GCD 攻击针对的是以密钥为变量的单变量方程。如果密钥在 $\mathbb F_q^m$ 中而不是 $\mathbb F_q$，那么此攻击无法直接应用。

不变子域攻击

如果轮常量或线性层选择不当，密文范围可能会被限制到子域。例如，考虑场是 $\mathbb F_{2^n}$，而 $\mathbb F_{2^m}$ 是 $\mathbb{F}_{2^n}$ 的一个子域。这意味着 $m$ 是 $n$ 的因子。如果 MiMC 中所有轮常量 $ci$ 和密钥 $k$ 都在子域 $\mathbb F_{2^m}$ 中，攻击者可以通过选择明文 $x \in \mathbb F\{2^m}$ 来确保 $Ek(x) \in \mathbb F_{2^m}$，从而将可能的密钥空间从 $2^n$ 减小到 $2^m$——例如，在 MiMC 中，如果场是 $\mathbb F\{2^{128}}$，且所有轮常量 $ci$ 和密钥 $k$ 在 $\mathbb F_{2^{64}}$ 中。那么，如果攻击设置为明文攻击，如果明文在 $\mathbb F_{2^{64}}$ 中，攻击者可能会注意到密文总是在 $\mathbb F\{2^{64}}$ 中。因此，攻击者只需测试 $2^{64}$ 个密钥候选而不是 $2^{128}$。

通过选择随机轮常量，例如无内藏数字，这项攻击可以被轻松预防。换句话说，如果某个实现使用自定义轮常量，并且背后的选择理由未披露，则可能会对不变子域攻击有漏洞。请注意，不变子域攻击只对二进制领域有效，因为素域没有子域。

线性化

线性化是一种通过将每个单项式转换为新变量，将多元方程表示为线性方程的技术。考虑以下 $\mathbb F_{11}$ 中的多元方程：

$$ \begin{aligned} x_1 + x_2x_3 = 6\ x_1x_2 + x_1x_3 + x_1 = 3\ x_2x_3 + x_2 = 2\ x_1x_2 + x_1 + x_3 = 8\ x_1x_2 + x_1x_3 + x_3 = 7\ x_2x_3 + x_1 + x_2 = 2 \end{aligned} $$

然后，通过将每个单项式替换为新变量如下，

$$ \begin{aligned} x_1 = y_1\ x_2 = y_2\ x_3 = y_3\ x_1x_2 = y_4\ x_1x_3 = y_5\ x_2x_3 = y_6 \end{aligned} $$

方程组会变成一个线性方程系统，可以通过高斯消去法轻松求解。

让 $n$ 为唯一单项式的数量，$m$ 为方程的数量。通过线性化解决给定方程时，必须满足 n≤mn \leq mn≤m，并且时间复杂度为 $O(n^\omega)$，其中 $\omega$ 是矩阵乘法复杂度的最小指数。矩阵中的每个元素在乘法前至少应检查一次，因此 ω 的下界为 $\omega = 2$。而当前的state-of-the-art↗ 算法是 $\omega = 2.371866$。为了抵抗线性化攻击，设计者应声称单项式的数量 $n$ 足够大，使得攻击复杂度高于预期的安全参数。

例如，对于 $\mathbb F_q$，如果 $q \approx 2^{128}$，设密钥为 $k = (k_0, k_1, k_2) \in \mathbb F_q^3$。设计者想展示这个原语具有 128 位的安全性。如果 $E(k, x)$ 具有最大次数 $2^{48}-1$，那么从方程构造的单项式的数量大约为 $2^{48 \times 3} = 2^{144}$，因为 $k_1, k_2, k_3$ 的次数在 $0$ 到 $2^{48}$ 之间变化。那么线性化的时间复杂度为 $O((2^{144})^\omega) \geq O(2^{288})$，即使我们假设 $\omega = 2$。因此，该原语对线性化攻击是安全的。

与此同时，重要的问题是是否所有的单项式确实会出现。如果表达式是稀疏的，而且大部分单项式实际上并没有出现，那么该攻击可能是可行的。因此，设计者应该理论上声称大部分单项式已经出现，或者通过使用玩具参数进行实验性展示。

Gröbner 基底攻击

Gröbner 基底攻击是一种通过计算 Gröbner 基底解决多元系统的方法。AOCs 的代数结构使我们能够为密钥和中间值构建多元方程。例如，让我们考虑三轮 MiMC。设 I1I_1I1​ 和 I2I_2I2​ 分别为第一和第二个 S-盒的输出。

然后，给定明文-密文对 $(x, y)$，我们有一个多元系统：

$$ \begin{aligned} (x+k)^3 - I_1 = 0\ (I_1 + k + c_1)^3 - I_2 = 0\ (I_2 + k + c_2)^3 - k - y = 0\ \end{aligned} $$

与单变量系统 y=(((x+k)3+k+c1)3+k+c2)3+ky = (((x+k)^3 + k + c_1)^3 + k + c_2)^3 + ky=(((x+k)3+k+c1​)3+k+c2​)3+k 相比，这个多元系统的好处在于方程的次数要低得多。如果我们能为 k,I1,I2k, I_1, I_2k,I1​,I2​ 解决这个多元系统，那么钥匙就找回来了。然而，单变量方程如果次数不太高，通过 Kaltofen-Shoup 算法这样的广为人知的算法很容易解决，而对多元系统并没有有效算法。

Gröbner 基底攻击并不是直接解决多元系统，而是多元方程的 Gröbner 基底始终包含一个单变量方程。一旦找到给定方程的 Gröbner 基底，我们就会获得可以解决的单变量方程。

那么什么是 Gröbner 基底呢？理解 Gröbner 基底需要非常高水平的数学能力；因此，我们只想提供一个简要的概述而省去细节。要更深入地了解这方面的技术知识，建议参考这篇论文↗。

让我们考虑以下多元系统：

$$ \begin{aligned} f_1 &: x^2 - y^3 - y - 1 = 0\ f_2 &: -xy + x - y = 0 \end{aligned} $$

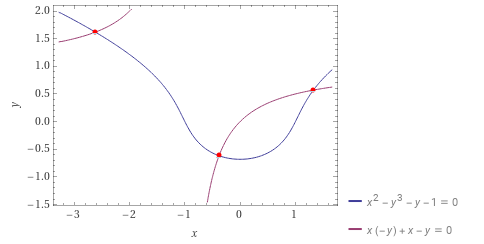
我们可以通过计算 $f' = m_1 \cdot f_1 + m_2 \cdot f_2$ 找到另一个多元方程，其解决方案与上述多元系统相同，其中 $m_1$ 和 $m_2$是单项式。例如，我们选择 $m_1 = y$和 $m_2 = x$。然后 $f_3 = m_1 \cdot f_1 + m_2 \cdot f_2 = y(x^2 - y^3 - y - 1) + x(-xy + x - y) = -y^4 - y^2 - y + x^2 - xy$ 。显然，系统 ${f_1, f_2}$的解决方案也是 $f_3$ 的解决方案。

给定多元系统的 Gröbner 基底是通过适当地重复上述计算来获得的。Gröbner 基底具有重要特性：

1. 从 Gröbner 基底导出的系统解与原始多元系统相同，以及
2. Gröbner 基底具有单变量方程。

例如，${f_1, f_2}$ 的 Gröbner 基底是 ${g_1 = x + y^4 - y^3 + y^2 - y - 1, g_2 = y^5 - 2y^4 + 2y^3 - 2y^2 - y + 1 }$。由于 $g_2$ 是 $y$ 的单变量方程，因此通过 $g_2$ 恢复 $y$。之后，通过将 $y$ 代入获得的解中来恢复 $x$。通过 Gröbner 基底恢复的 $(x, y)$ 也是原系统的解。

红线（相应地蓝线）表示 $g_1$ （相应地 $g_2$）的零点。图像由 WolframAlpha 创建。

总而言之，Gröbner 基底攻击遵循以下步骤。

1. 计算 Gröbner 基底。
2. 在给定基底中找到单变量多项式并计算其根。
3. 将此解决方案代入 Gröbner 基底并重复步骤 2。

让我们考虑 Gröbner 基底攻击的时间复杂度。对于具有度数 $d_1, \dots, d_L$ 的 $L$ 方程，在 $n$ 个变量上，我们定义 $P(x) = \frac{\prod_i(1-x^{d_i})}{(1-x)^n}$.

正则度 $D_r$ 定义为 $P(x)$ 中第一个非正系数的项的次数。计算 Gröbner 基底的时间复杂度估计为 $\binom{n + D_r}{D_r}^\omega$，其中 $n$ 是变量的数量，$D_r$ 是正则度。

这个值可能不直观，但可以理解为随着变量数量 $n$ 的减少，方程的数量 $L$ 增加，而方程的次数 $d_i$ 减少，系统变得更容易受到攻击。

攻击示例

一般来说，设计者会考虑上面所有攻击在原语中，并选择自己的轮数。然而，对于每种结构可能存在变种，攻击者试图找到它们以破解原语。

我们将介绍几种针对 ZK 友好哈希函数的攻击。这些攻击导致规范的改变或设计的撤回。

对 MiMC 的插值攻击

第一个攻击是针对 MiMC 的插值攻击，由 Chaoyun Li 和 Bart Preneel 提出（见这篇论文↗）。我们已经讨论，对于 $r$ 轮的 MiMC，插值多项式的次数 $d$ 是 $d=3^r$。攻击者需要至少 $3^r+1$ 对来构造这个多项式，时间复杂度为 $d\log d $。此外，内存复杂度为 $(3^r + 1) \cdot |\mathbb F| $ 代表了存储每个系数所需的总内存。MiMC 设计者声称，如果内存复杂度有限，则可以减少轮数。例如，作者建议当可用字节限制在 $2^{64}$ 字节时，38 轮对于 MiMC-129/129 是足够的。

然而，Li 和 Preneel 找到了构造部分多项式的新攻击。这种攻击只使用了微不足道的内存。尽管攻击者可能有 $3^r+1$ 个数据点，但由于内存限制，不可能恢复准确的多项式。然而，仅仅恢复插值多项式的第二高项是可能的。（有关更多信息，请参见论文中的第 3.3 节。）一旦从插值中恢复了第二高项，密钥 $k$ 的值可以由第二高项确定，即 $3^r \cdot k$。

这项攻击表明，对于 MiMC-129/129，即使在攻击者可用内存受限的情况下，完整的 82 轮都是必要的。然而，这些结果并不影响完整轮 MiMC 的安全主张。

还有另一项针对 MiMC 的更高阶差分密码分析攻击（欲了解更多信息，请参阅这里↗）。然而，这项攻击比暴力攻击快，但需要 $2^{n-1}$ 是二进制域 $\mathbb F_{2^n}$ 的选择数据。因此，它没有被视为现实威胁。

对 Jarvis 和 Friday 的 Gröbner 基底攻击

Jarvis 和 Friday 是 ZK 友好的块密码和哈希函数（阅读更多信息在这里↗）。由于 Friday 是 Jarvis 的 Merkle-Damgård↗ 结构，仅讨论 Jarvis 的结构就足够了。与 AES 中使用的 S-盒类似，Jarvis 使用逆 S-盒作为非线性层。$\mathbb F_{2^n}$ 中的逆 S-盒定义为 $inv(x) = x^{2^n-2}$。如果 $x = 0$，则 $inv(x) = 0$，其他情况下 $x \times inv(x) = 1$。

Jarvis 的结构相对简单。轮函数由逆 S-盒、次数为 $4$ 的多项式 $B$ 和 $C$ 组成。$B(x)$ 和 $C(x)$ 的构成如下：$B(x) = b_4 \cdot x^4 + b_2 \cdot x^2 + b_1 \cdot x^1 + b_0 \cdot x^0$ 和 $C(x) = c_4 \cdot x^4 + c_2 \cdot x^2 + c_1 \cdot x^1 + c_0 \cdot x^0$。这些方程与 Vision 中使用的那些相同。最后，Jarvis 的一轮可以表示为 $\textsf{Jarvis}_i(s) = C(B^{-1}(inv(s))) + K_r$，其中 $i$ 代表轮数索引。

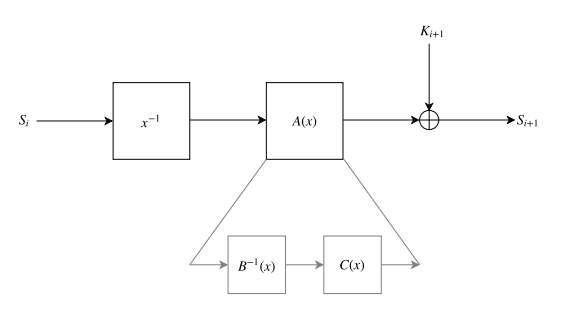
在他们的密钥调度中也使用了逆 S-盒，如下所示。

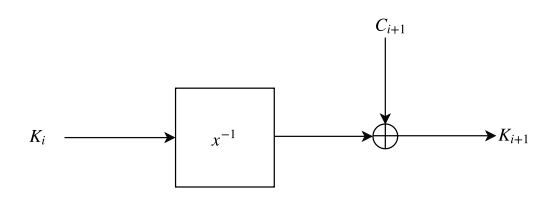
即使仅使用一个或两个逆 S-盒，也可以实现最大次数。此外，SNARK/STARK 的成本相对较低，因为只需验证 $x(1-xy) = 0$ 和 $y(1-xy) = 0$ 即可检查 $y = inv(x)$。作者考虑了几种攻击，并建议对于 $n = 128, 160, 192, 256$，使用 10、11、12 和 14 轮。

然而，他们没有考虑 Gröbner 基底攻击，依据这篇论文↗，Jarvis 对此类攻击是脆弱的。

如果仅将密钥视为变量，则等式为单变量。然而，高度很高，使得恢复密钥非常困难。然而，如果我们将每个中间值都添加为变量，系统就变得多元。通过这些中间值，次数显著降低，从而允许进行 Gröbner 基底攻击。

对于每一轮，$x_i = B^{-1}(inv(s))$ 被视为变量。

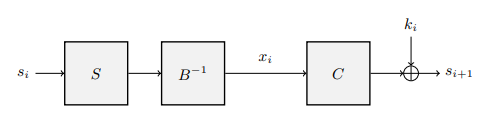
给出以下方程：

• $(C(x_i) + ki) \cdot B(x\{i+1}) = 1$：次数为 $8$ 的 $r-1$ 个方程。
• $B(x_1) \cdot (p + k_0) = 1$：一个次数为 $5$ 的方程。
• $C(x_r) = c + k_r$：一个次数为 $4$ 的方程。
• $(k_{i+1}+c_i) \cdot k_i = 1$：次数为 $2$ 的 $r$ 种方程。

存在 $2\cdot r+1$ 个变量 $x_1, \dots, x_r$ 和 $k_0, \dots, k_r$，共 $2\cdot r+1$ 个方程。不幸的是，这仅攻击了 Jarvis 的简化轮，但通过论文中建议的优化，变量数量减少，成功攻击到 Jarvis 的完整轮（见论文的第 4.2 节）。

通过这项攻击，我们意识到利用中间变量，表达式可以以另一种形式呈现，从而使攻击可能。特别地，ZK 友好哈希函数往往允许在效率的良好转换中以低次数表示表达式，但必须小心不要使其脆弱于 Gröbner 基底攻击。

对 Starkad 的不变子空间攻击

Starkad 是一个 ZK 友好的哈希函数，其结构与 Poseidon 相同，唯一的区别是 Starkad 使用二进制域，而 Poseidon 使用素域。Poseidon 的作者最初提出了 Starkad 和 Poseidon，但他们已经撤回了 Starkad。

让我们回顾一下 Starkad 的结构。中间的 S-盒层由部分 S-盒层组成。这将减少 R1CS 或 AET 成本。

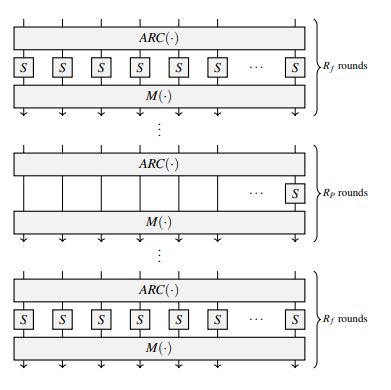
线性层的目的是将局部变化传播到整个状态。在 Starkad 中，线性层是一个 Cauchy 矩阵↗，其定义为 $M[i,j] = \frac{1}{x_i + y_j}$，用于 ${xi}{1 \leq i \leq m}$ 和 ${yi}{1 \leq i \leq m}$ 的条目，这些条目是成对不同的，并且 $x_i + y_j \neq 0$，其中 $i \in {1, \dots, m}$ 和 $j \in {1, \dots, m}$。为了生成序列 ${xi}{1 \leq i \leq m}$ 和 ${yi}{1 \leq i \leq m}$，首先需要选择一个常数 $r$ 和一个起始点 $x_0$。变量 $x_i$ 和 $y_i$ 定义如下： $x_i = x_0 + i - 1$ 和 $y_i = x_i + r$。矩阵一旦生成并固定，设计者选择 $x_0 = 0$ 和 $r = m$，其中 $m$ 表示每层中的字数。

然而，这个 MDS 矩阵允许存在大型不变子空间，这些不变子空间穿过整个中间部分 S-box 的轮次而未激活任何 S-box。这使得中间 $R_P$ 轮次变得线性，如 攻击论文↗ 中所指出的。更精确地说，对于某个不变子空间 $V$，如果 $\Delta \in V$ 且 $x \oplus y = \Delta$，则 $F(x) \oplus F(y) = L(\Delta)$，其中 $F$ 代表中间层，而 $L$ 代表线性变换。这在统计和代数密码分析方面影响了安全性。

尽管可以通过选择一个不被 4 整除的 $m$ 值或选择另一个安全的 MDS 矩阵来缓解此攻击，但设计者决定放弃 Starkad，仅保留 Poseidon。

结论

在本帖中，我们讨论了几种代数攻击及其在原数中的用途。在设计新的 AOCs 时，请务必考虑它们是否能够抵御此帖中提到的攻击。这是一个活跃的研究领域，因此建议定期查看像 Cryptology ePrint\ Archive↗ 这样的地方以获取新的攻击。

关于我们

Zellic 专注于保护新兴技术。我们的安全研究人员发现了最有价值目标中的漏洞，从财富 500 强到 DeFi 巨头。

开发人员、创始人和投资者信任我们的安全评估，以便快速、自信且没有重大漏洞地进行发布。凭借我们在现实世界攻防安全研究中的背景，我们发现了其他人可能遗漏的内容。

‍ 联系我们↗，获得比其他公司更好的审计服务。真实的审计，而不是走形式。

• 原文链接： zellic.io/blog/algebraic...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～