EIP-4844 的 Proof of Equivalence 機制介紹

本文將介紹 Validity Rollup 如何利用 Proof of Equivalence 機制來驗證放在 Blob 裡的交易的真實性。

Photo by Tolga Ulkan on Unsplash

先備知識：

• 知道 Rollup 的運作方式以及「資料發布」（aka Data Publication、Data Availability）的問題
• 知道 Optimism Rollup 與 Validity Rollup 的不同
• 知道用來儲存區塊鏈狀態的「狀態樹」與「狀態根」是什麼
• 知道 Merkle Proof 與 Commitment 的意義與用途

關於 EIP-4844、Blob 的介紹可以參考：

Rollup 的大補帖：Proto-Danksharding（一）

為什麼會需要煩惱交易的真實性？

在 EIP-4844 之後，Rollup 可以選擇將交易資料寫在 Blob 裡，Rollup 合約沒辦法直接存取到 Blob 的內容，但使用 Blob 比使用 Calldata 還便宜非常多。

對 Rollup 來說，將交易上傳至 L1 的目的就是藉由 L1 來確保「交易資料已發佈」。如果是 Optimistic Rollup，它只需要將交易資料丟到一個大家都可以存取到的地方，確保未來如果需要利用交易資料來發起挑戰時，有人手上有這些資料即可。所以不管交易資料是放在 Calldata 還是 Blob，對 Optimistic Rollup 來說都沒有差別。

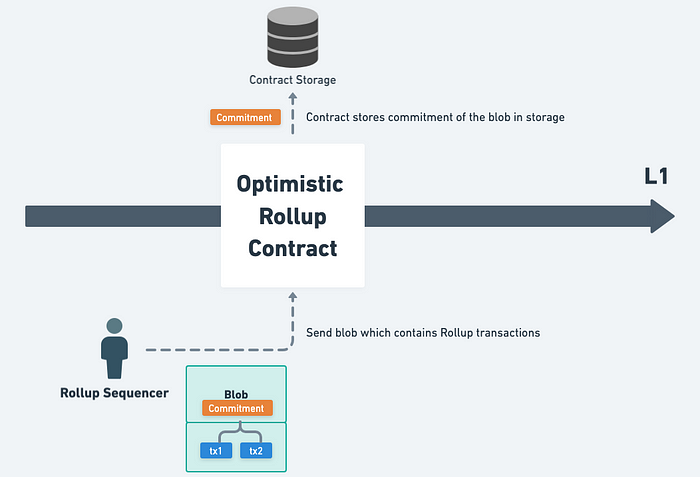
Optimistic Rollup 只要確保交易有被發布，在未來需要發起挑戰時可以用到就好，所以不管交易是放在 Calldata 或 Blob 都不影響安全性

但如果 Validity Rollup 將交易資料放到 Blob 裡，它就需要額外確認 Blob 裡的交易資料的真實性，為什麼呢？

Validity Rollup

在 EIP-4844 以前，Validity Rollup 將交易資料及 Validity Proof 都放在 Calldata 裡，因此 Validity Rollup 在 L1 上的合約可以同時存取到交易資料與 Validity Proof，便可以輕鬆確認「這個 Proof 驗證的是這些交易執行完的結果」。

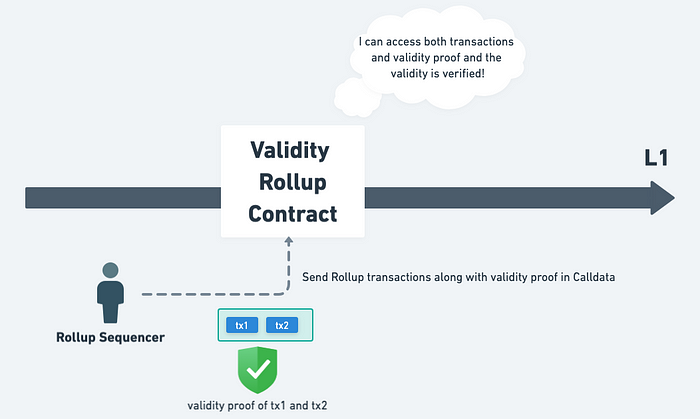
因為可以存取得到交易資料，所以把交易資料和 Validity Proof 一起拿去驗證就可以知道這些交易執行完的狀態的有效性

但在 EIP-4844 後，如果 Validity Rollup 將交易放在 Blob，Validity Rollup 合約就存取不到完整的交易資料，只能存取到交易資料的 Commitment，那 Validity Rollup 要怎麼知道 Commitment 背後所代表的交易真的和 Validity Proof 所要證明的交易是同樣一批交易？

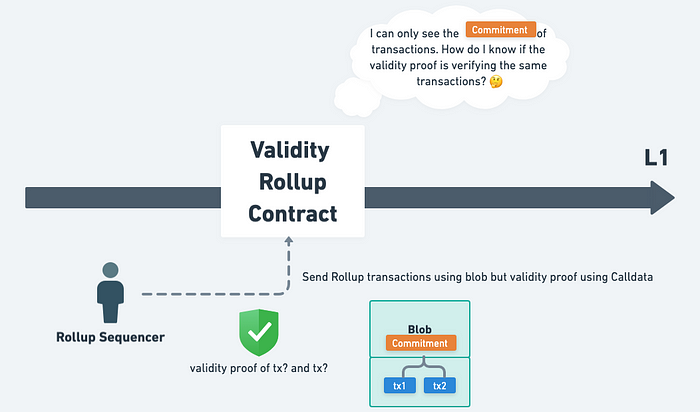
Blob 裡放 tx1 和 tx2，但 Validity Proof 可能是證明不一樣的交易，如果沒有完整的交易資料去搭配 Validity Proof 做驗證，要怎麼知道這兩邊的交易是一樣的？

惡意的 Sequencer 可以在 Blob 裡放 tx1 與 tx2，但實際上 Validity Proof 是在驗證 tx3 與 tx4 執行完的結果，如果沒有加入檢查機制，那就會發生除了惡意 Sequencer 之外沒人有 tx3 與 tx4 的資料，所以沒有人能夠算出 tx3 與 tx4 執行後的最新狀態（他們只知道 tx3 與 tx4 執行完的狀態「根」，不知道完整的狀態「樹」）。

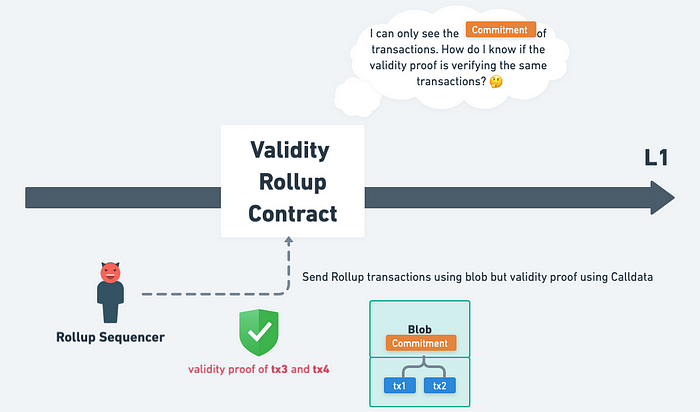
大家看的到 tx1 與 tx2，但一點用也沒有，因為 Validity Proof 證明的是 tx3 與 tx4

解法一：在 Validity Rollup 的電路裡也加入 Blob Commitment 的計算過程

這是最直接的解法，Validity Rollup 配合 EIP-4844 修改其 ZK 電路，將計算 Blob Commitment 的步驟也加入其中，如此 Validity Proof 驗證時雖然只有 Commitment，但它知道這個 Commitment 背後是它處理過的交易，所以便不需擔心 Blob 裡可能放的是不一樣的交易。

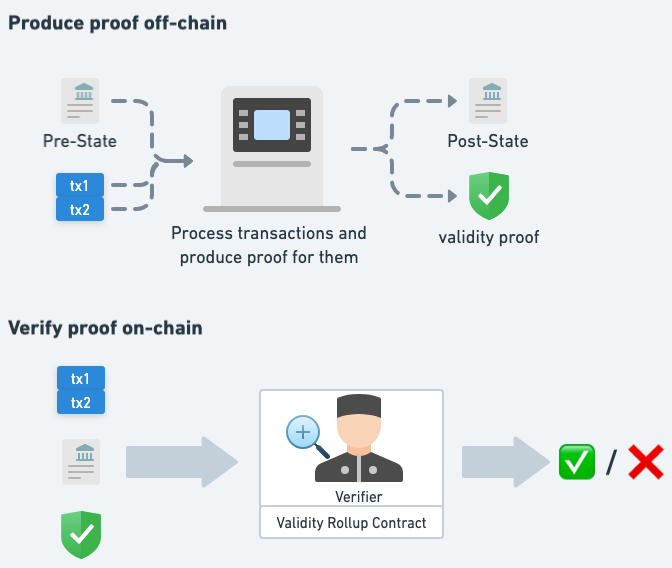
原本 Validity Proof 驗證時會搭配交易資料一起驗證，所以可以確定彼此綁定的關係

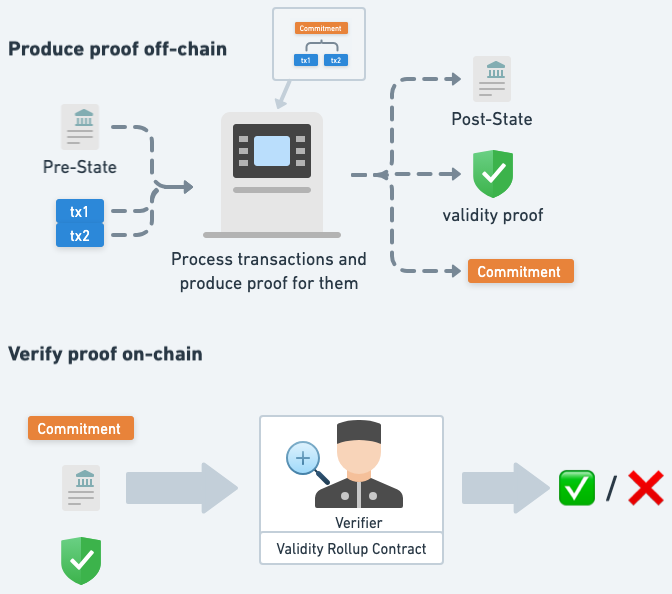
如果驗證時只證下一個 Commitment，那就是電路中要包含計算 Commitment 的過程，如此我們才可以被說服電路處理的交易資料和 Commitment 背後的交易資料是一樣的

但計算 Blob 裡資料的 Commitment 是使用 KZG 這個 Polynomial Commitment 設計來計算，而某些 Validity Rollup 要在其電路裡做 KZG 運算會遇到產生零知識證明成本會提高的缺點。

註：Polynomial Commitment 是另外一種 Commit 的方式。相較於 Merkle Tree 是將分段資料視為葉節點並做出一棵 Merkle Tree 得到 Merkle Tree Root 作為 Commitment 值，Polynomial Commitment 則是將分段資料先轉換成一個 Polynomial（多項式），再對這個多項式進行 Commit 得到 Commitment。和 Merkle Tree Root 搭配 Merkle Proof 可以驗證那棵 Merkle Tree 某個葉節點的值一樣，Polynomial Commitment 中透過 Commitment 和 Proof 也可以驗證這個多項式在不同點上的取值。

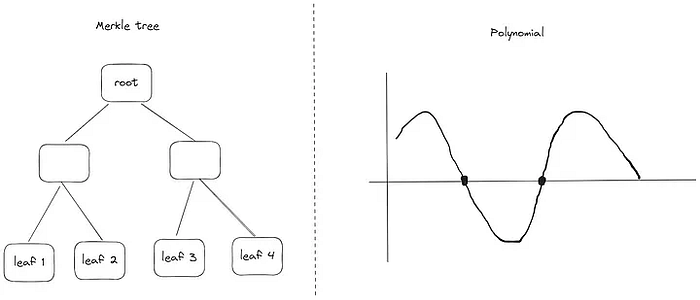
Merkle Tree vs. Polynomial (Commitment)。 source

解法二：Proof of Equivalence

因此 Vitalik 提出了 Proof of Equivalence 機制 讓 Validity Rollup 用不同的（成本較低的） Polynomial Commitment 去 Commit 資料的同時，一樣能證明「雖然 KZG Commitment 值和我的 Polynomial Commitment 算出來的值不一樣，但背後所 Commit 的資料是一樣的」。

如此 Validity Rollup 就能各自用自己適合的 Polynomial Commitment 設計去 Commit 交易資料，不影響產生零知識證明的成本，然後在 L1 上的 Validity Rollup 合約裡透過 Proof of Equivalence 去證明「Blob 裡的交易資料真的是我這次零知識證明所驗證的交易」。

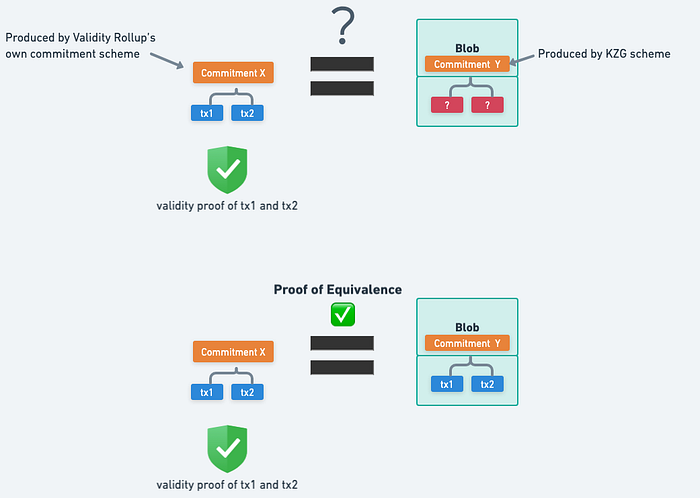
Proof of Equivalence 包含一個 Proof，用來證明 Equivalence，即 「Commitment X 裡的內容和 Commitment Y 裡的內容一樣」。要怎麼證明這件事呢？我們不能單純將交易資料直接做兩次 Polynomial Commitment（一次是 KZG），然後產出一個零知識證明來證明這件事，因為這就等價於解法一：在 ZK 電路裡直接做 KZG 運算。因此我們用另外一個方式來證明 — 利用隨機數與機率。

隨機取值

對兩個不同的 Polynomial 來說，「隨機」挑一個點去對它們分別取值，「得到一樣的值」的機率非常非常低。以下圖為例，這兩個多項式相交的點是 (x=0, y=0) 及 (x=2, y=8)，在 x=0 與 x=2 之外的地方兩個多項式的 y 值都不會是一樣的，也就是不會取到一樣的值的意思。

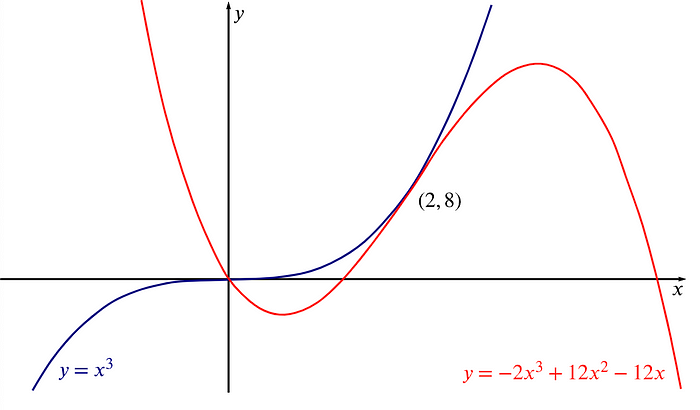
在廣袤無垠的平面上，也就只有兩個點會是 x1=x2, y1=y2。 source

所以當我們隨機挑選一個點去對兩個 Polynomial 分別取值，如果這兩個值不一樣，那就表示這兩個 Polynomial 是不一樣的，在我們的情境裡這就代表兩組交易資料是不一樣的；如果這兩個值一樣，那這兩個 Polynomial 是不一樣的機率非常非常非常低，低到我們可以相信它們是一樣的，也就是兩組交易資料是一樣的。

那這個「隨機挑選的點」是怎麼決定的？因為如果攻擊者可以決定或猜到這個「隨機」的點，那他就只需要確保兩組交易資料的 Polynomial 在那個點的值是一樣的就可以騙過 Proof of Equivalence 機制。

Fiat-Shamir Transformation

Proof of Equivalence 利用 Fiat-Shamir Transformation 來挑選要取哪個點的值，而不是交由某個人來選擇。Fiat-Shamir Transformation 透過密碼學雜湊函式來算出隨機數，而函式的輸入就是交易資料。假設由交易資料組成的 Polynomial 為 P(x)，以下是產生 Proof of Equivalence 的大致步驟：

1. Validity Rollup 以自己的 Polynomial Commitment 算出交易資料的 Commitment 值（這裡稱為 Commitment X）
2. 接著同樣以 KZG 算出交易資料的 Commitment 值（這裡稱為 Commitment Y）
3. 然後將 Commitment X 與 Y 丟進雜湊函式，得到隨機數（稱為 z），假設 P(z) = a
4. 最後生成一個 Proof π 用來證明「 a 為 Commitment Y 的 Polynomial 在 z 點的值」

步驟 1 與 3 會在電路裡運算；步驟 2 則不會在電路裡運算，而是由 Rollup Sequencer 算好再餵給電路，作為綁定 Commitment Y 的用途；步驟 4 也是 Sequencer 產生，只是不是給電路，而是送到鏈上驗證 Proof of Equivalence。

註：不管 Sequencer 塞什麼 KZG Commitment 值給電路都不影響交易正確性，因為電路已經有它所需的所有資料來驗證交易，而且電路裡本來不會進行 KZG 運算或驗證。因此步驟 2 的 Commitment Y 只是作為綁定用途：如果 Sequencer 偷偷把 Commitment Y 換成 Commitment W ，到時候到鏈上驗證 Proof of Equivalence 時會失敗。

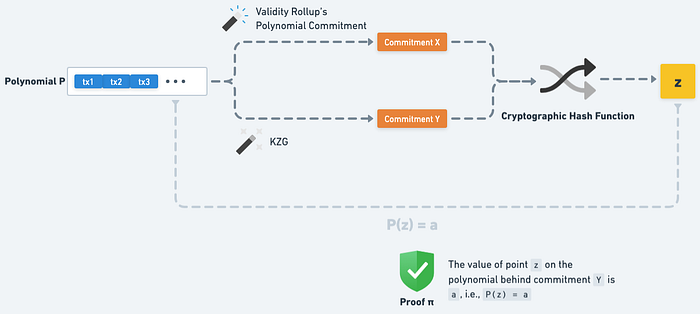
隨機值 z 會由 Commitment X 與 Y 經過雜湊韓式所算出，Proof π 則是用來證明 P(z) = a

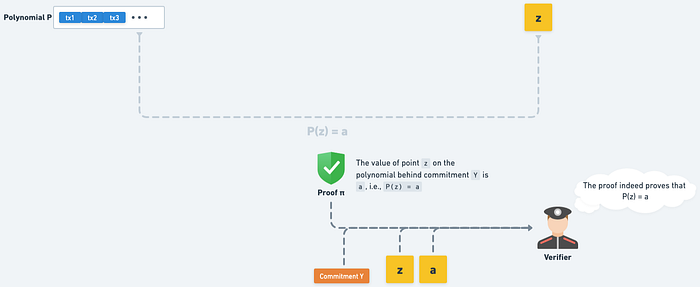
z, a, Commitment Y 再搭配 π 就能證明「P 的 KZG Commitment 是 Y，且 P(z) = a」

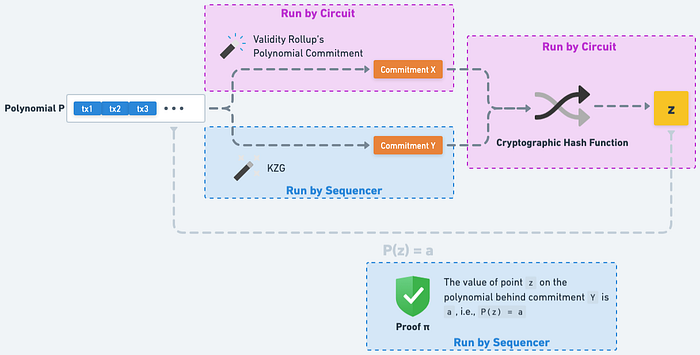
紫色部分會由電路計算；藍色部分則是 Sequencer 來計算，其不影響安全性

上鏈證明

接著就可以將 Rollup State 的 Validity Proof 及 Proof of Equivalence 帶上鏈去驗證：

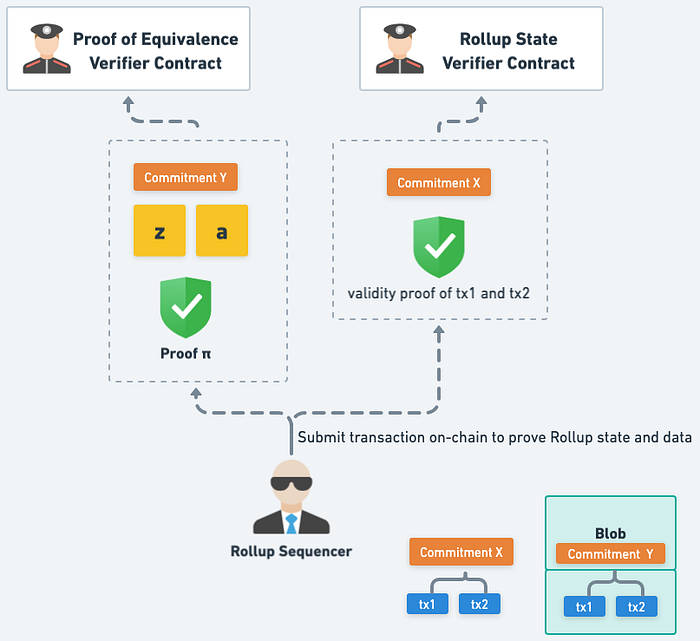
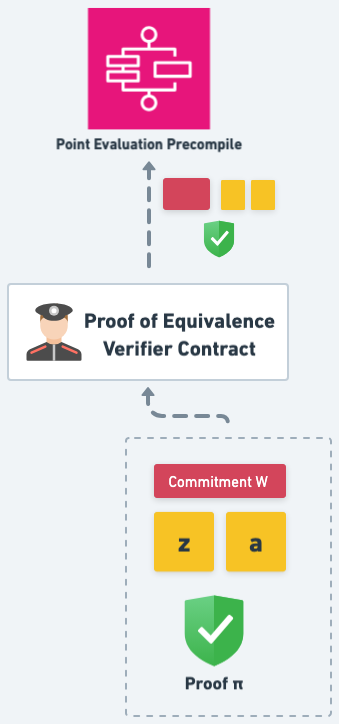
左邊虛線的部分用來證明 Proof of Equivalence；右邊虛線的部分是原本的 Rollup Validity Proof

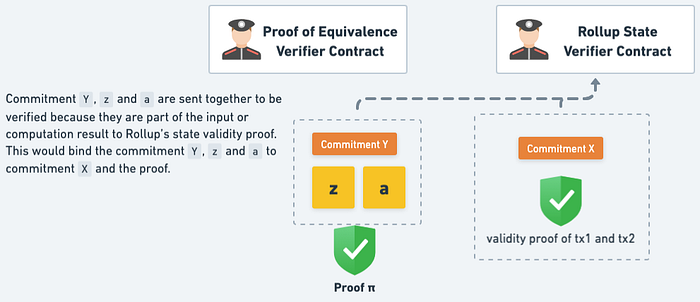
不過實際上驗證 Validaity Proof 時還是需要 Commitment Y, z 及 a。因為 Commitment Y 是作為電路的 Input 由 Sequencer 輸入，而 z 與 a 則是電路所產生的 output，這些值要一起搭配 Validity Proof 驗證才會通過

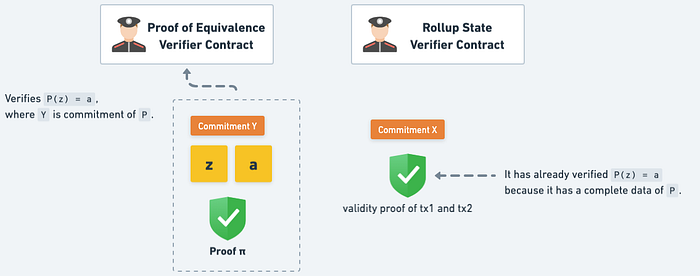
左邊則是如前面所述，z, a, Commitment Y 再搭配 π 就能證明「P 的 KZG Commitment 是 Y，且 P(z) = a」

這裡為了方便解釋所以將合約分開成 Proof of Equivalence Contract 和 Rollup State Verifier Contract，但實際上兩個部分是合併在一起的，而不是分開驗證。只有一起驗證通過才能證明 Proof of Equivalence，即

• 電路裡驗證「 P 的 Polynomial Commitment 是 X，且 P(z) = a」
• 然後再透過 π 驗證「 P 的 KZG Commitment 是 Y，且 P(z) = a」

如此便能相信 X 與 Y 所 Commit 的資料是同一份。

如果餵不同的 KZG Commitment 值

如果 Sequencer 餵 Commitment Y 給電路，但實際上 Blob 裡放不一樣的交易資料，那就會產生不一樣的 Commitment：

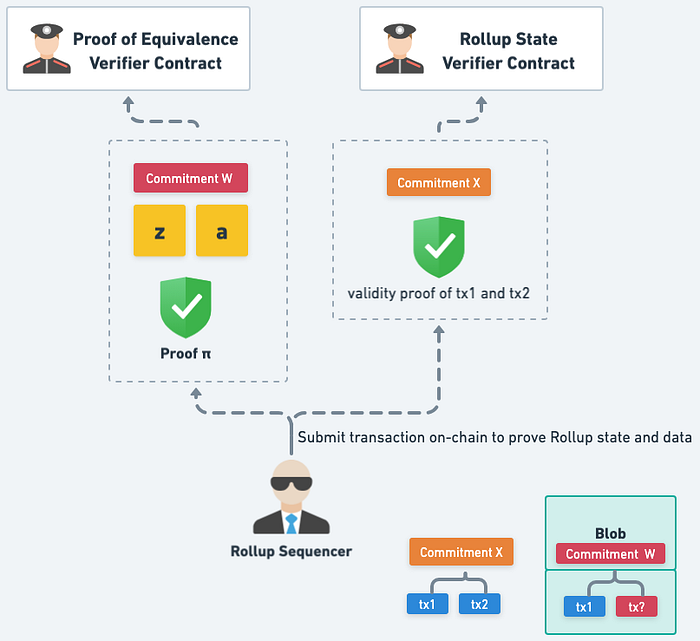
這樣 Validity Proof 就會驗證失敗，因為 Commitment W 不是當初 Sequencer 給它的 Commitment：

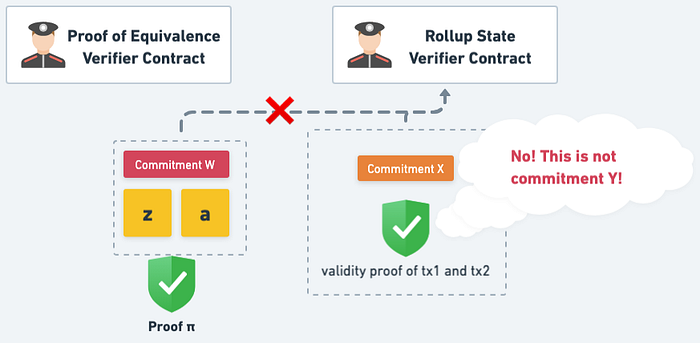
如果試圖想騙過 Proof of Equivalence 機制

那 Sequencer 是否可以保持 P(z) = a 不變，但是不斷微調 P 裡其他的值，反正只要 P(z) = a 驗的過就能說服 Rollup 交易資料是一樣的？

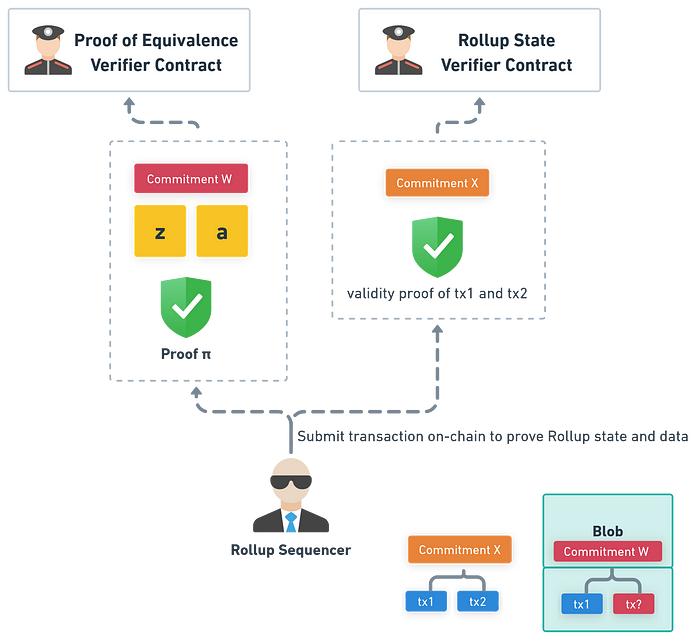
Sequencer 保持 P(z) = a 但是修改其他地方，得到 Commitment W，並把 W 餵給電路

不過因為 z 這個值是 Commitment X 和 Commitment Y 一起算出來的，所以當 Y 的值改變了，算出的值也不會再是 z，因此 Sequencer 原本保持 P(z) = a 就沒有意義了。而且即便只修改 P 裡的一個值也會導致 P 變成完全不一樣的多項式 P’，而如同最前面所述，兩個不同的多項式所相交的點數量非常非常少，因此 P(k) 的值幾乎不可能等於 P’(k) 的值。

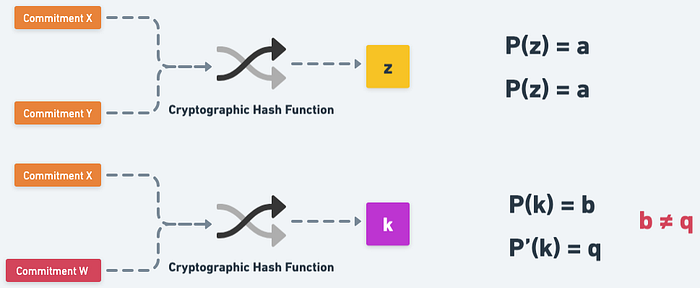
想偷換多項式裡的值，但也會因此導致雜湊函式所算出來的隨機數不一樣，而 P(k) != P’(k)

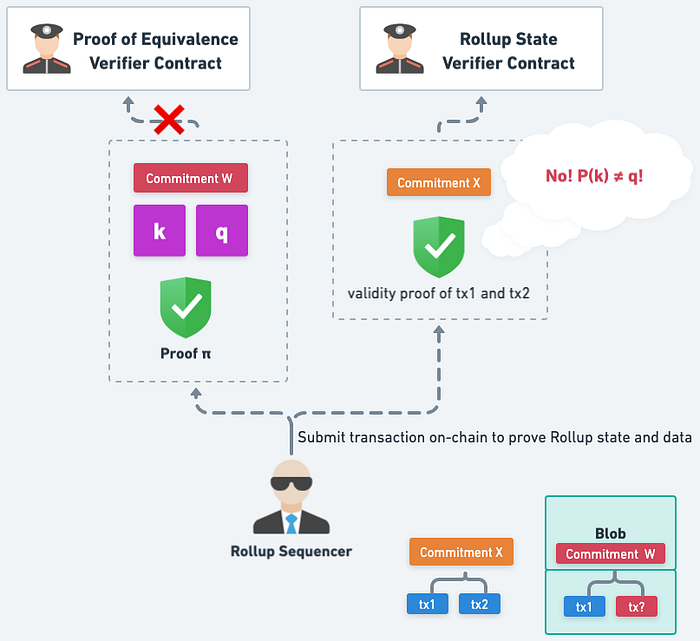
電路裡會知道 P(k) = b，因此把 k 與 q 拿去驗證會失敗

Sequencer 這時必須重新再來一次，只是這次變成要維持 P(k) = b 不變，看新算出來的隨機數會不會剛好等於 k。他可以一直不斷重複嘗試，但成功機會渺茫，因為要破解密碼學雜湊函式的難度太高了。

註：在 L1 合約裡驗證 Proof of Equivalence 實際上會透過 Point Evaluation Precompile 來驗證 P(z) = a，透過 Precompile 的運算成本會低很多。

以上就是 Validity Rollup 如何將交易資料放在 Blob 節省成本的同時，利用 Proof of Equivalence 這個技巧證明 Blob 裡的交易資料真的和 (State) Validity Proof 所處理的交易資料是一樣的。只需要在電路及 L1 合約裡多做一些處理和運算就可以享受到大幅降低資料成本的優點。

總結

• Validity Rollup 如果將交易放在 Calldata，讓合約可以存取得到，那就可以自然地相信 Validity Proof 證明的真的是這批交易的結果。只是交易資料放 Calldata 的成本很高
• 如果改成把交易資料放在 Blob，成本很低但是合約存取不到，這時候要怎麼知道 Validity Proof 證明的是不是 Blob 裡放的交易？
• 最直接的解法是在 Validity Rollup 的電路裡直接做一次 Blob 裡的 Commitment 運算，也就是 KZG Commitment，但 KZG 對某些零知識證明系統來說成本太高
• 透過 Proof of Equivalence，我們可以以很便宜的方式驗證 Validity Rollup 的 Commitment 和 Blob 裡的 KZG Commitment 是不是對同一批交易資料所做的 Commitment。如此 Validity Rollup 就不需要在電路裡做 KZG 運算，而是可以用適合自己的 Commitment 方式
• L1 合約只需要再多驗證 P(z) = a 就能被說服兩個 Commitment 是對同樣的資料做 Commit，但是 z 是怎麼決定的？如果攻擊者可以任意挑選 z，那他用不同資料 Commit 來騙過 L1 合約就變得非常簡單
• 因此我們透過 Fiat-Shamir Transformation 並搭配交易資料當 Input 來決定 z 的值，如果攻擊者修改了任意一丁點的交易資料內容，都會得到完全不一樣的隨機值，因此他要想騙過 L1 合約得先破解密碼學雜湊函式，而這基本上是不可能的

參考資料與推薦延伸閱讀

• https://consensys.io/blog/ethereum-evolved-dencun-upgrade-part-5-eip-4844
• https://ethresear.ch/t/easy-proof-of-equivalence-between-multiple-polynomial-commitment-schemes-to-the-same-data/8188
• https://eips.ethereum.org/EIPS/eip-4844#point-evaluation-precompile
• StarkNet 介紹 4844 與 Proof of Equivalence 實作設計
• ZKSync 的 4844 技術文件與實作程式碼： 1、 2、 3
• https://github.com/taikoxyz/raiko/issues/47

TEM Medium 2024 有獎徵稿

TEM Medium 目前正在進行有獎徵稿！詳情請參考：

TEM Medium 2024 有獎徵稿

Special thanks to Anton Cheng and Cyan Ho for reviewing and improving this post

• 本文转载自： medium.com/taipei-ethere...