可变速率GDA - 调整价格来控制代币的发行速度
- Paradigm
- 发布于 2022-08-25 14:59
- 阅读 1282
本文介绍了一种新的代币发行机制,即可变速率GDA(VRGDA),通过调整价格来控制代币的发行速度,使其接近自定义的时间表。当销售进度超前于时间表时提高价格,而当销售进度落后于时间表时降低价格,是对GDA机制的推广。文中给出了机制的概述和Solidity实现,以及几个示例时间表。
概述
本文介绍了一种新颖的代币发行机制。可变速率 GDA (VRGDA),专为 Art Gobblers 设计并在 0xMonaco 中使用,使你可以通过在销售领先于计划时提高价格,在销售落后于计划时降低价格,从而随着时间的推移以接近自定义计划的价格出售代币——这是 GDA 机制的推广。
我们提供了该机制的概述以及核心机制和几个示例计划的高度优化、可用于生产的 Solidity 实现。
动机
Art Gobblers 是 Justin Roiland 和 Paradigm 的一项数字艺术实验。该项目的一个重要目标是创建一个自我维持的生态系统,该生态系统可以在没有人为干预的情况下在未来几年蓬勃发展。
该系统中有两个核心 NFT,我们希望任何人都能随时购买其中任何一个。
我们希望首先相对较快地发行两者。随着时间的推移,一个达到固定供应量的上限,而另一个则永远以缓慢的恒定速率发行。
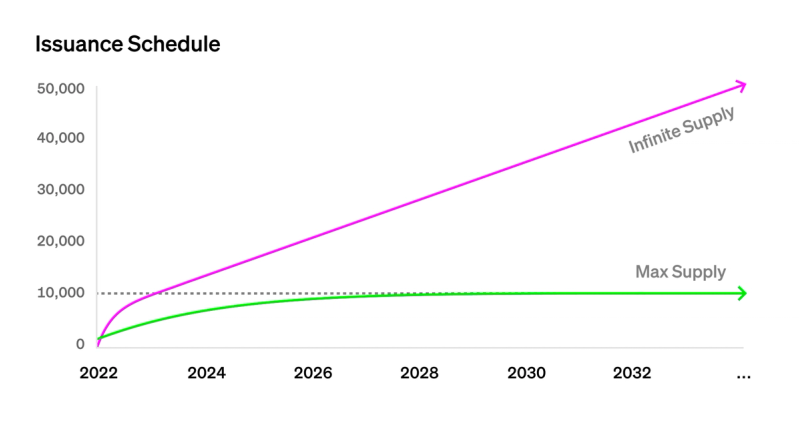
我们力求在保持无缝用户体验的同时实现这些目标,这将允许用户随时购买 NFT,而无需例如等待预定的拍卖。
我们的解决方案是 VRGDA,它是 GDA 的一种泛化,它允许任意调度 NFT 的发行,而不是标准 GDA 的统一线性调度。
机制
构建直觉
假设有一个简单的计划,我们每天要出售 10 个 NFT。我们将第一个 NFT 的起始价格设置为 1 个代币。
假设现在是第 5 天,因此我们应该已经售出 50 个 NFT。但是,需求很高,我们已经售出了 70 个。我们本不应该在第 7 天之前售出 70 个 NFT,因此我们提前了两天。
因此,我们希望在未来收取更高的价格。我们使用指数曲线来确定高多少。这可能会因参数而异,但在这种情况下,我们假设我们使用 $2^\text{days ahead of schedule}$,因此我们将价格提高了一个因子$2^2=4$ 因此,由于我们的初始价格是 1 个代币,新价格将是 4 个代币,从而更难以购买更多的 NFT。
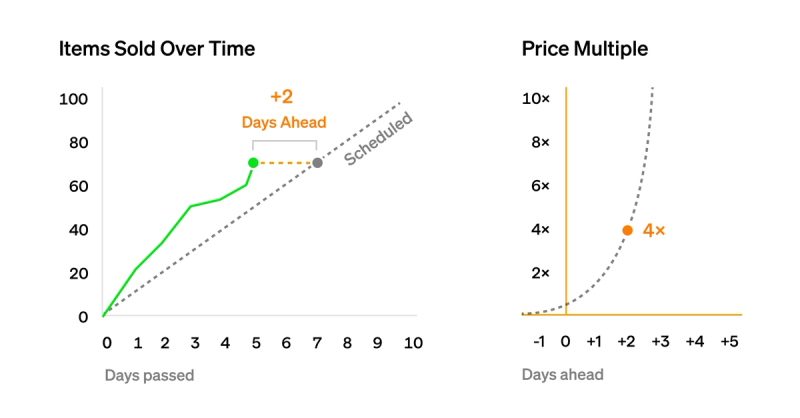
十天后,在第 15 天,我们应该已经售出 150 个 NFT,但是用户仅购买了 120 个,即他们应该在第 12 天购买的数量,这意味着我们落后计划三天。我们将价格调整为,使用户更容易购买更多的 NFT。

十天后,在第 15 天,我们应该已经售出 150 个 NFT,但是用户仅购买了 120 个,即他们应该在第 12 天购买的数量,这意味着我们落后计划三天。我们将价格调整为 $2^{-3}=0.125 $ ,使用户更容易购买更多的 NFT。
构建
参数
$p_0$ - 如果完全按计划出售 NFT,则 NFT 的售价(目标价格)。
k - 在没有购买的情况下,NFT 价格在单位时间内降低的百分比。
f(t) - 发行计划:将 t 映射到计划在该时间售出的 NFT 数量。
目标
我们希望按照特定的时间表发行 NFT。我们将使用的机制是,如果 NFT 的销售领先于计划,则提高价格;如果 NFT 的销售落后于计划,则降低价格。如果销售完全按计划进行,则购买下一个 NFT 的价格将保持不变。
定义
假设我们要按照由$f(t)$ 描述的计划出售 NFT,该计划将时间点映射到我们希望在该时间之前已售出的 NFT 的累计数量。例如,如果我们想每两天出售一个 NFT,我们将定义 $f(t)$ 如下所示:
$f(t) = \frac{t}{2}$
还假设我们要为每个 NFT 使用单独的荷兰式拍卖出售我们的 NFT。如果我们设置每个 NFT 的起始价格为 1,并让该价格以每单位时间 的速率衰减,而没有销售,那么如果在时间 $t$购买,它的价格将是:
$(1-k)^t$ 为了给自己提供实现目标所需的灵活性,我们可以将拍卖的起始点在时间上偏移某个
$s_n$,我们将在下面进行推导,以便在时间 $t$的价格为:
$(1-k)^{t-s_n}$ 如果我们希望目标价格与 1 不同,我们可以乘以一个常数
$p_0$。我们称此调整后的价格为$\texttt{vrgda}_n(t)$:
$\texttt{vrgda}_n(t) = p_0(1-k)^{t-s_n}$
确定 $s_n$
根据我们的发行计划 $f$ , 我们想要在时间$t_n$出售第 $n$个 NFT。 我们可以通过反转$f$来定义$t_n$,以获得从$n$到应该出售的时间的映射:
$t_n = f^{-1}(n)$
VRGDA 目标的一个结果是,如果$n$个 NFT 完全按照其发行计划的目标时间购买,则其价格将为 $p_0$。 正式表达,这意味着如果我们以完全按照目标速率进行销售,那么在时间$t_n$, 第$n$个 NFT 的价格将为:
$p_0(1-k)^{t_n-s_n}=p_0$
通过划分$p_0$进行简化,我们知道以下内容应始终为真:
$(1-k)^{t_n-s_n}=1$
这意味着 $t_n-s_n=0$ 或者 $s_n=t_n$ 。 使用我们上面对$t_n$的定义,我们知道 $s_n = f^{-1}(n)$。
最终公式
通过将$s_n$的这个定义代入$\texttt{vrgda}_n(t)$,我们最终得到以下最终公式:
$\texttt{vrgda}_n(t) = p_0(1-k)^{t-f^{-1}(n)}$
简单的发行计划
下面我们演示如何导出一些简单的发行计划以与 VRGDA 公式一起使用。
线性
假设我们要每天出售$r$个 NFT。 那么 $f(t) = rt$,所以$f^{-1}(t) = \frac{t}{r}$ 将此$f^{-1}(t)$插入 VRGDA 定价公式后,我们最终得到以下结果:
$\texttt{linear_vrgda}_n(t) = p_0(1-k)^{t-\frac{n}{r}}$
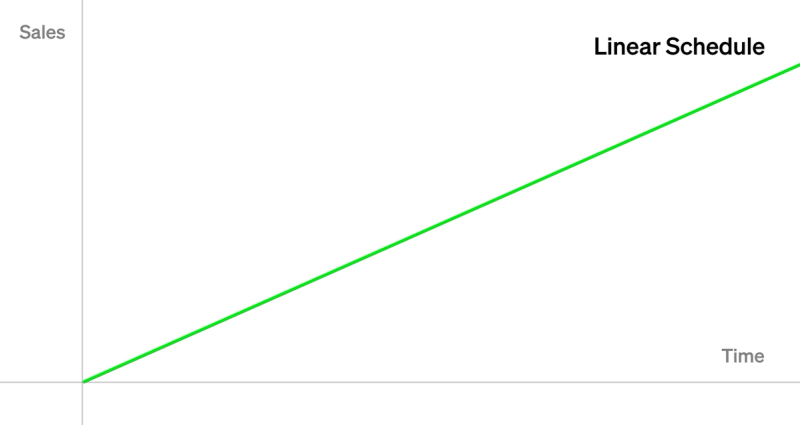
请注意,这与 GDA 同构,这就是为什么我们称 VRGDA 为 GDA 的推广。
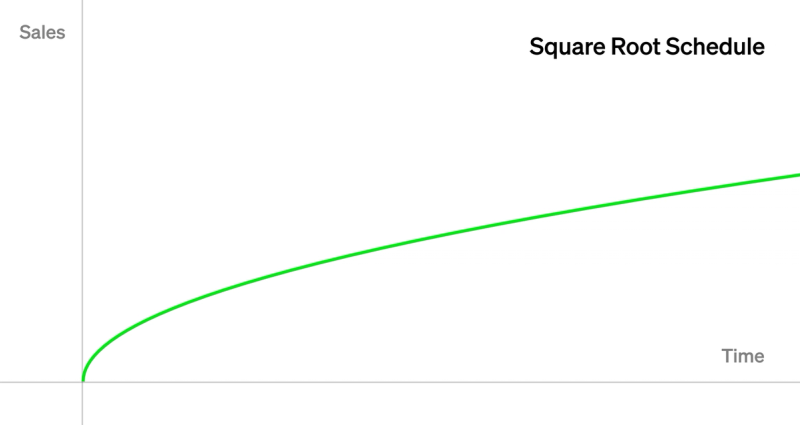
平方根
假设我们要以与时间的平方根成比例的速率发行 NFT——例如,首先更快地发行 NFT,然后随着时间的推移发行得更慢,但永远不会停止。
然后,我们可以设置$f(t) = \sqrt{t}$ ,这样在第 1 天,我们售出 1 个 NFT,在第 4 天,我们售出 2 个,在第 9 天,我们售出 3 个,依此类推。
在这种情况下,$f^{-1}(n) = n^2$。 现在,我们只需插入 VRGDA 定价公式即可得到:
$$\texttt{sqrt_vrgda}_n(t) = p_0(1-k)^{t-n^2}$$
Logistic 发行计划
与上面的示例相比,Logistic 发行计划有些复杂。 但是,我们仍然选择详细介绍它,因为它提供了一种引导初始增长的方式,而无需强制执行无限的通货膨胀机制。
动机
假设我们想首先快速发行 NFT,然后放慢速度,直到最终发行某个最大数量,就像 Art Gobblers 中的情况一样。
对此建模的一种简洁方法是使用具有正域的 logistic 函数。
推导 $f$
Logistic 函数是一条 S 形曲线。 我们将对其进行稍微简化,并将其定义为:
$$ l(t) =\frac{1}{1 + e^{-t}} $$
当$t$接近负无穷时,此曲线接近 0,当 $t$接近无穷时,此曲线接近 1。
对于我们的特定应用程序,我们不想使用完整的 S 曲线(尽管也可以使用完整的 Logistic VRGDA,它会先慢下来,然后加速,然后再慢下来)。 相反,我们只想使用曲线中$t$为正的部分。
因为$l(0)=0.5$,但是我们希望我们的计划表示在时间 0 出售 0 个 NFT,所以我们需要通过减去 0.5 来向下移动此函数。 这条新曲线将从 0 到 0.5:
$$ h(t) =\frac{1}{1 + e^{-t}}-0.5 $$
我们要发行$L-1$个 NFT(我们选择这个是为了符号方便,因为该函数会在达到 $L$之前趋于稳定),因此我们需要将该函数缩放一个因子 $2L$。
我们还可以引入一个时间缩放参数$s$来调整发行 NFT 的速度:
$$ f(t) =\frac{2L}{1 + e^{-st}}-L $$
为了选择 $s$,观察到:
$$ \frac{f(t)}{L}=\frac{2}{1 + e^{-st}}-1 $$ 此外:
$$ \frac{f(\frac{1}{s})}{L}=\frac{2}{1 + e^{-1}}-1\approx0.46 $$
这意味着我们可以通过选择我们希望大约 46% 的 NFT 被发行的时间来选择$s$。 例如,如果我们希望 46% 的 NFT 在 100 个时间单位后发行,这意味着 $\frac{1}{s}=100$,所以$s=\frac{1}{100}$。
公式
取上面 $f(t)$的倒数得到:
$$ f^{-1}(n) = - \frac{\text{ln}\left(\frac{2L}{L+ n} - 1\right)}{s} $$
将所有这些放在一起,我们最终得到以下公式:
$$ \texttt{logistic_vrgda}_n(t) = p_0(1-k)^{t+ \frac{\text{ln}\left(\frac{2L}{L+ n} - 1\right)}{s}} $$

实现
在 transmission11/VRGDAs 可以找到 VRGDA 和各种发行计划的高度优化、可用于生产且许可宽松 (MIT) 的实现。 欢迎提出改进意见的 Pull Request。
结论
VRGDA 提供了一种使用几乎任何你想要的计划发行 NFT 的方法,同时仍然允许用户随时无缝购买它们。
在 Art Gobblers 的案例中,它们使我们能够自定义我们的社区增长和 UGC 动态。 在 0xMonaco 的案例中,它创造了一个具有挑战性和高度竞争性的游戏循环。
我们相信在 NFT、链上游戏、DeFi 等领域还有许多其他潜在应用。 如果你想探索它们,我们很乐意听取你的意见。 你可以在 Twitter 上通过 @transmissions11、@FrankieIsLost 和 @_Dave__White_ 与我们联系。
我们迫不及待地想看看你构建的内容。
鸣谢: Dan Robinson, samczsun, Riley Holterhus, NN Blossoms, dcfpascal, kootsZhin, Grug, Ben Leimberger, Kiran Cherukuri, Aaru, eva
图形由:Achal Srinivasan
- 原文链接: paradigm.xyz/2022/08/vrg...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~

