Gossipsub网络直径估算 - 网络
- 以太坊中文
- 发布于 2025-01-24 23:28
- 阅读 1086
本文提出了一个随机理论模型,用于估算Gossipsub网络中消息传播的速度(即直径)。通过分析仅广播方法,固定网格度数和随机连接,发现以太坊网络的Gossipsub直径为7。该模型考虑了重复消息,并有助于优化协议以减少不必要的开销。文章还讨论了性能评估、协议优化和弹性洞察等实际应用。
TL;DR
ProbeLab 团队 ( probelab.io) 一直在广泛研究以太坊网络中 Gossipsub 的行为(参见最近的帖子)。现在,我们提出了一个新的随机理论模型,以估计消息在 Gossipsub 网络中传播的速度(其直径)。通过专注于仅广播方法,并使用固定的 mesh degree 和随机连接,我们的分析发现以太坊网络的 Gossipsub 直径为 7。
Introduction
在这篇文章中,我们开发了一个理论模型,用于估计 Gossipsub 网络的直径。我们所说的“直径”,是指消息到达系统中所有节点所需的最大跳数(或离散时间步数)。该指标可以直接洞察广播在网络中传播的速度。此外,理解直径有助于推断冗余(重复)消息,并为如何优化协议以最大程度地减少不必要的开销提供指导。
分析网络直径和重复消息率可产生实际效益:
- 性能评估:量化传播速度使我们能够评估节点是否及时接收到关键数据。
- 协议优化:观察重复消息的分布可以发现减少带宽消耗和网络拥塞的机会。
- 弹性洞察:了解最坏情况下的传播路径可以指导改进,从而在各种压力条件下提高可靠性。
为了集中我们的分析,我们做了几个假设:
- 仅广播模型:我们只考虑 Gossipsub 的 pub-sub(广播)方面,忽略其“gossip”组件。
- 恒定的 mesh degree:网络中每个节点的 mesh degree D 都是固定的。
- 随机图拓扑:每个节点精确地连接到 D 个随机选择的 peer。所有链接都是双向的,确保图是连通的。
- 静态 mesh:假设在传播过程中 mesh 保持静态。
- 统一的链路延迟:所有 peer 在网络延迟方面彼此等距。
这些假设使我们能够建立一个随机模型,该模型在保持易于处理的同时,仍然能够捕获 Gossipsub 网络的关键属性。在以下章节中,我们将逐步开发此模型,并说明其对消息传播的影响。
Intuition
让我们考虑一个简单的例子,说明消息如何在每个节点有四个连接的网络中传播 (D=4)。当一个节点第一次收到消息时,我们称它被“感染”了。在下一轮中,新感染的节点将消息发送给自己的邻居,邻居们也会被感染。一步一步地,我们看到广播如何在网络中传播,直到所有节点都收到消息。
Round 0
在最开始,我们只有一个持有消息的“感染”节点。
Round 1
在这一轮中,原始节点将消息发送给它的 D=4 个邻居。这四个节点被“感染”,并且现在都知道了广播。反过来,他们将在下一轮中传播消息。
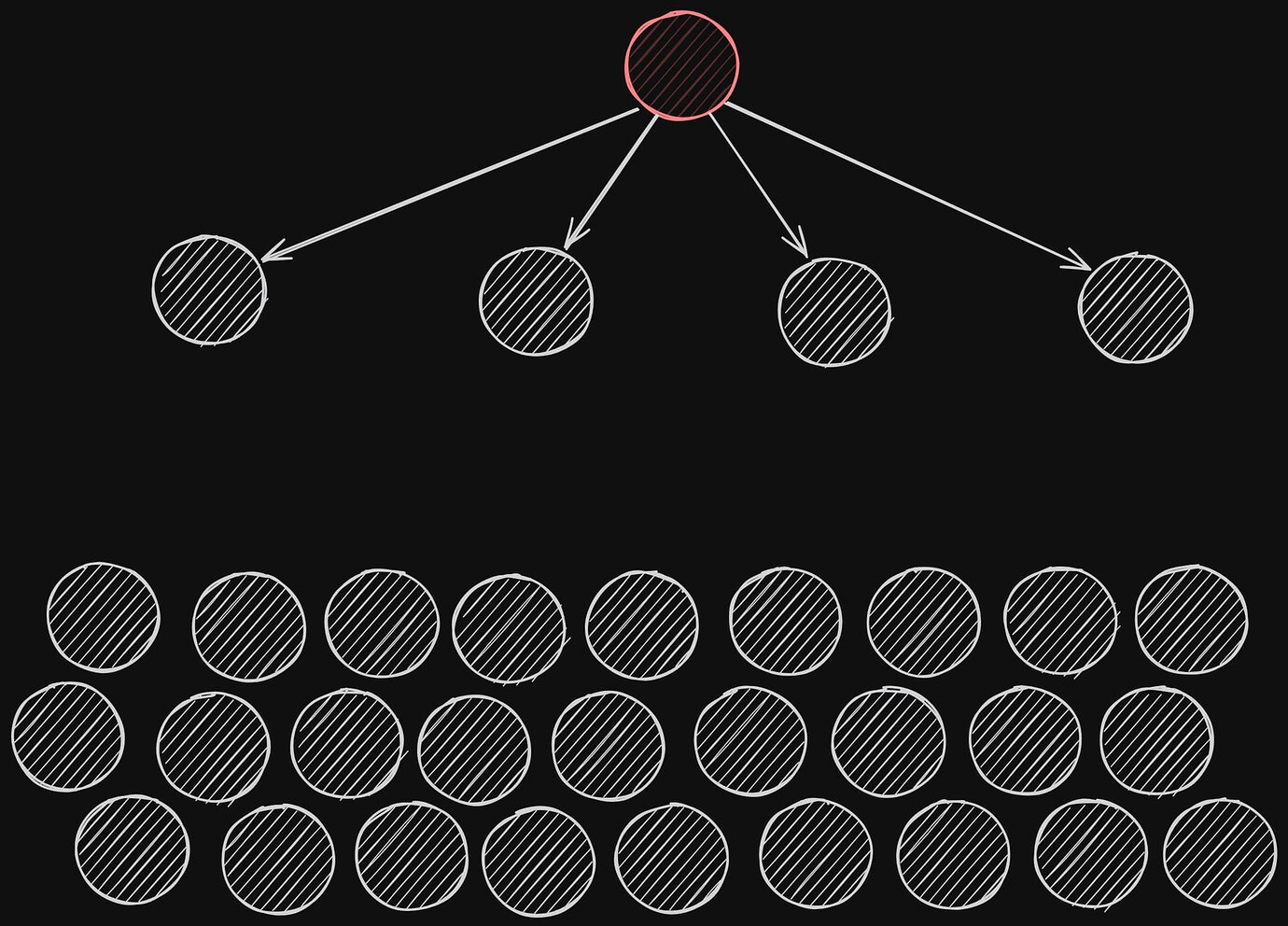 \
Infection process: round 11920×1382 213 KB
\
Infection process: round 11920×1382 213 KB
Round 2
四个新感染的节点中的每一个都重复广播,将其发送给他们自己剩余的三个邻居。(1) 请注意,两个 peer 可能会尝试感染同一个尚未感染的节点。(2) 另请注意,在前一轮中被感染的两个节点可能彼此连接,并尝试相互感染,即使它们都已经感染。
在计算下一轮中感染的节点数量时,重要的是要考虑到这两种重复情况。
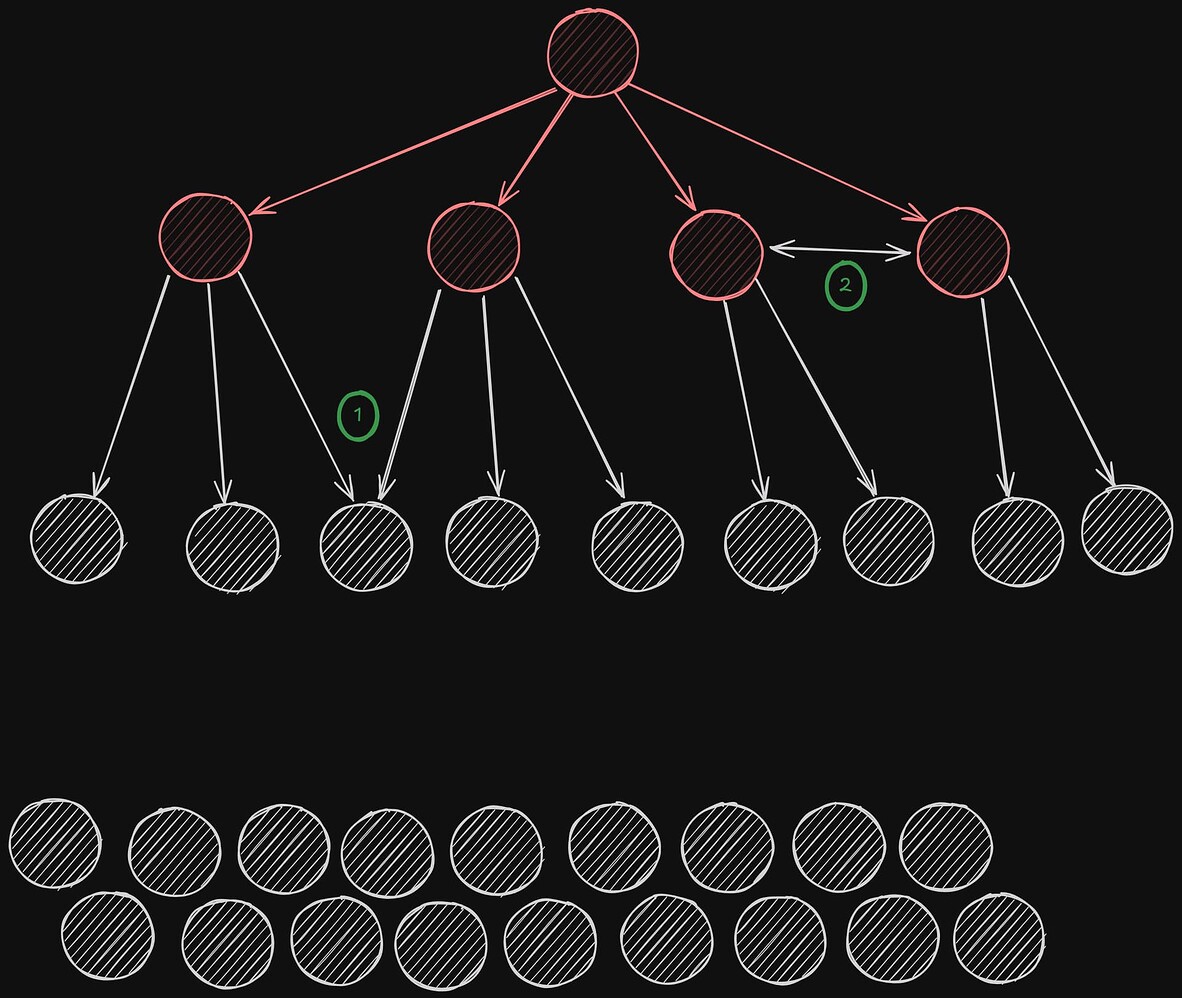 \
Infection process: round 21920×1623 204 KB
\
Infection process: round 21920×1623 204 KB
Round 3
在第三个传播步骤中,我们简单例子中的大多数或所有可到达的节点都将被感染。(1) 请注意,在前一轮中被感染两次的节点只能感染另外两个节点,而不是三个。这是因为所有节点都有精确的 D=4 个连接,并且传出消息的数量正好是 D 减去传入消息的数量。(2) 同样,被感染 4 次的节点,将不会在下一轮尝试感染任何其他节点,因为它没有额外的链接。
随着受感染节点数量的增长,重复项的数量也会增加。
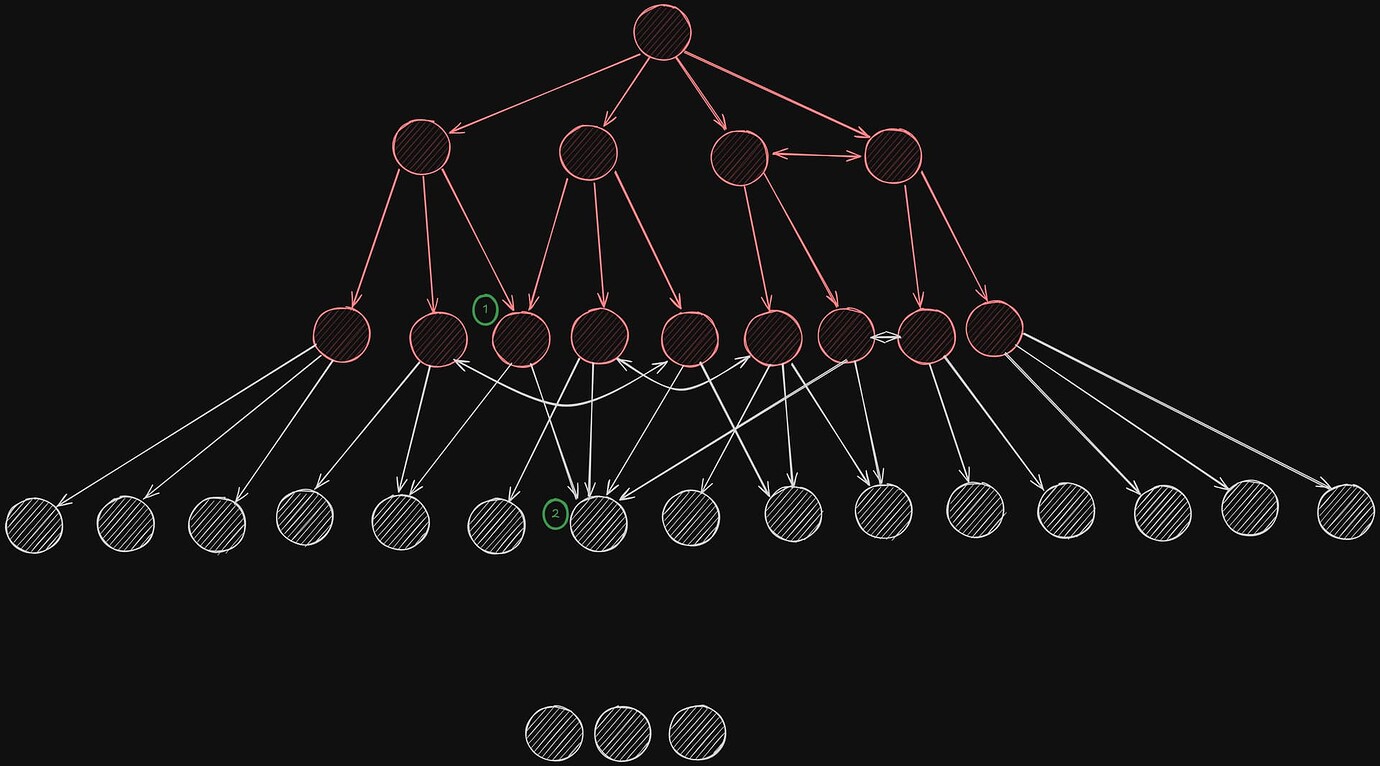 \
Infection process: round 31920×1068 99.2 KB
\
Infection process: round 31920×1068 99.2 KB
Round 4
在第四个也是最后一个传播步骤中,所有节点都已被感染。我们观察到,在这一点上,绝大多数感染实际上是重复的。(1) 请注意,在最后一轮中感染的节点可以彼此连接,这意味着将有第五轮,在这一轮中,这些节点再次相互感染。但是,此轮不计入网络直径,因为此时所有节点都已被感染。
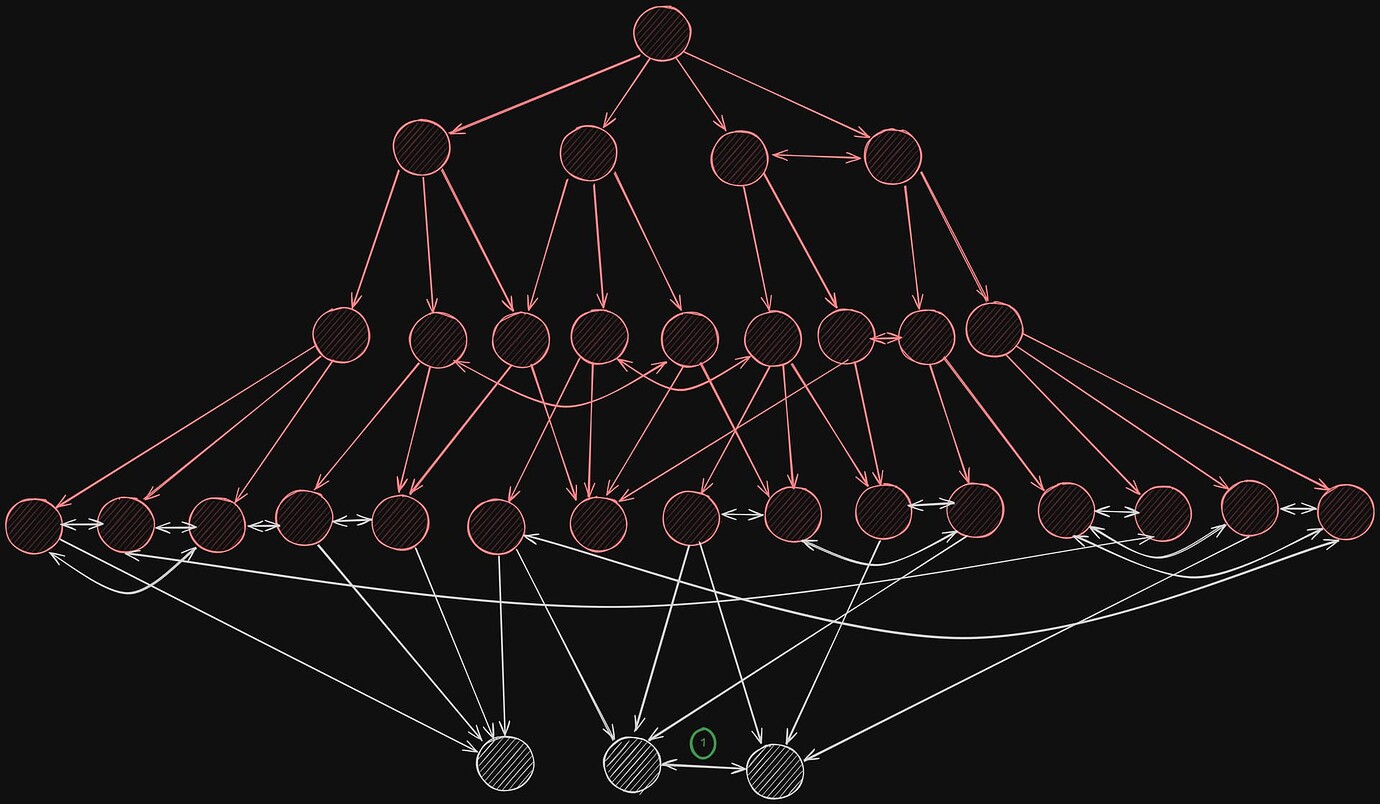 \
Infection process: round 41920×1120 123 KB
\
Infection process: round 41920×1120 123 KB
The maths
我们的目标是确定在每一轮 t 中,给定在第 t-1 轮中新感染节点的数量,有多少节点被新感染。跟踪跨轮的进展会显示网络中所有 N 个节点都已收到消息的点,从而使我们能够估计网络的直径。
Duplicates
如上所述,我们区分了重复感染的两个主要来源:同一层连接和下一层冲突。
- Same-layer connections
这些发生在同一轮中被感染并且也共享一条边的节点对之间。当这些节点尝试在下一轮中相互感染时,不会产生新的感染,因为它们已经被感染。
- Next-layer collisions
当一个节点在同一轮中收到多个初始感染时,就会出现这种情况。由于每个节点都有固定的 mesh degree D,因此每个“额外”的感染都会有效地减少它在下一轮中可以感染的新节点的数量。换句话说,已经被多个 peer 感染的节点不能使用相同的边来感染其他新的 peer,从而降低了其整体感染能力。
Definitions
- N:网络中节点的数量
- t:离散轮数 (t=0,1,2,...)。
- I(t):在第 t 轮首次被感染的节点数
- R(t):在第 t 轮或之前被感染的节点总数(累积)。形式上:
R(t) = R(t-1) + I(t)
- C(t):第 t 轮发生的下一层冲突的数量。当一个节点在同一轮中被多次感染时,就会发生冲突。例如,如果一个节点在第 t 轮被感染三次,则它对 C(t) 的贡献为 3-1=2,因为只有第一次感染才算作新的感染,其余 2 次是冗余的。
Initial case
在 t=0 时,我们从一个被感染的节点开始,也就是发布消息的节点,因此
I(0)=1, R(0)=1, C(0)=0
在 t=1 时,第 0 轮的单个被感染节点感染其 D 个邻居。没有下一层冲突,因为初始节点连接到的所有节点都是不同的。因此,
I(1)=D, R(1)=D+1, C(1)=0
Inductive Step
从 t=2 开始,同一层连接和下一层冲突都是可能的。
在第 t 轮,感染尝试次数 x_t 由下式给出:
x_t = (D-1) \times I(t-1) - C(t-1)
此公式考虑了以下几点:
- 在上一轮中恰好被感染一次的每个节点 (I(t-1)) 都有 D-1 个剩余链接可用于新的感染尝试。
- 我们从上一轮 (C(t-1)) 中减去下一层冲突,因为这些连接已经在上一轮的多次感染期间被消耗,并且无法重复使用。
此调整可确保 x_t 仅反映当前轮中可用于新感染的有效、未使用的链接。
让我们定义在第 t 轮开始时尚未感染的节点数。
M_t=N-R(t-1)
现在,我们可以通过确定第 t 轮的每个连接都不是同一层连接的概率来计算有多少感染尝试到达下一层(包括下一层冲突)。
y_t=x_t \times \frac{M_t}{N-R(t-2) -1}
以下是推理:
- 在第 t-1 轮感染的节点可能会连接到网络中的任何其他 N-R(t-2)-1 个节点(不包括它们自己)。
- 其中,M_t=N-R(t-1) 个节点仍未感染,因此有资格进行新的感染。
- 剩余的 I(t-1)-1 个节点表示在第 t-1 轮期间发生的感染。这些节点可能会形成同一层连接,这不会产生新的感染。
同一层连接的数量如下
x_t \times \frac{I(t-1)-1}{N-R(t-2)-1} = x_t - y_t
要计算新感染的数量,我们必须考虑并丢弃重复项。
单个感染尝试成功地将特定节点作为 M_t 个合格节点中的目标节点的概率为:
Pr[\text{infecting a specific node}] = \frac{1}{M_t}
在单次尝试中不感染此特定节点的概率为:
Pr[\text{not infecting a specific node}] = 1 - \frac{1}{M_t} = \frac{M_t-1}{M_t}
如果进行了 y_t 次感染尝试,则特定节点从未被感染的概率为:
Pr[\text{not infecting a specific node in } y_t \text{ attempts}] = (\frac{M_t-1}{M_t})^{y_t}
因此,在 y_t 次尝试中至少感染一次此特定节点的概率为:
Pr[\text{infecting a specific node in } y_t \text{ attempts}] = 1-(\frac{M_t-1}{M_t})^{y_t}
由于在本轮中有 M 个节点有资格被感染,因此新感染的预期数量为:
I(t) = \mathbb{E}[\# \text{ distinct newly infected peers}] = M_t \times [1-(\frac{M_t-1}{M_t})^{y_t}]
然后可以将下一层冲突的数量计算为总感染尝试次数与新感染节点数之间的差:
C(t) = y_t - I(t)
第 t 轮的重复项总数 D(t) 是下一层冲突和同一层连接的总和。
D(t) = (y_t - I(t)) + (x_t - y_t) = x_t - I(t)
有了这些公式,我们现在就拥有了运行模型所需的所有组件。
Results
在以太坊网络中,D=8 ( source),并且 N \approx 9,000 ( source)。对于这些参数,我们得出以下结果:
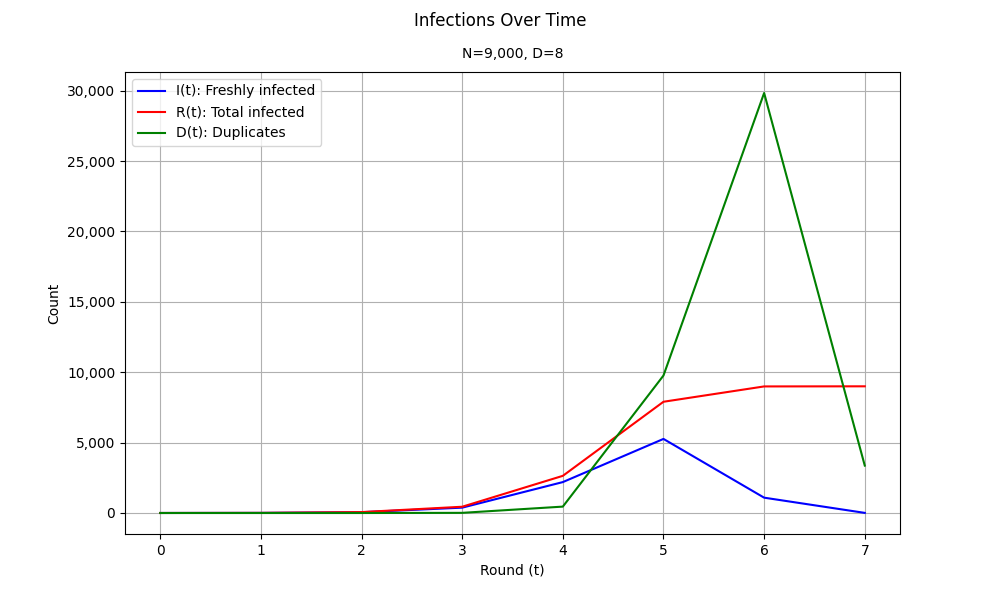 \
Gossipsub message propagation over time in the Ethereum network1000×600 37.8 KB
\
Gossipsub message propagation over time in the Ethereum network1000×600 37.8 KB
t= 0, I(t) = 1.00, R(t) = 1.00, D(t) = 0.00
t= 1, I(t) = 8.00, R(t) = 9.00, D(t) = 0.00
t= 2, I(t) = 55.79, R(t) = 64.79, D(t) = 0.21
t= 3, I(t) = 379.67, R(t) = 444.46, D(t) = 10.66
t= 4, I(t) = 2,195.63, R(t) = 2,640.08, D(t) = 453.79
t= 5, I(t) = 5,262.28, R(t) = 7,902.36, D(t) = 9,765.61
t= 6, I(t) = 1,089.18, R(t) = 8,991.54, D(t) = 29,836.48
t= 7, I(t) = 8.14, R(t) = 8,999.68, D(t) = 3,367.09Network Diameter
经过七轮后,平均有 8,999.68 个节点(共 9,000 个)被感染,这表明在某些情况下,可能需要额外一轮才能到达最后一个剩余节点。基于这些结果,在这些条件下将网络直径视为 7 是合理的。
Infections
正如预期的那样,新感染的数量稳步上升,直到第五轮达到转折点。之后,随着未感染节点池的缩小并且变得难以到达,它开始下降。
Duplicates
一个特别值得注意的观察结果是,在第五轮和第六轮期间,重复消息的数量激增。发生这种激增的原因是,在前一轮中,许多节点都被新感染,但可用的未感染目标更少,从而导致了更多的冗余传输。
预计每个节点平均发送和接收 D-2 个重复项(source)。但是,当我们将此模型应用于以太坊网络时,我们发现每个节点平均约有 4.83 个重复项(大约 D-3)。这种差异的出现是因为我们的随机模型以离散步骤工作,并没有完全捕获重复项的与时间相关的性质。然而,我们希望该模型能够准确地表示重复项的分布方式,特别是考虑到在消息传播的后期阶段往往会出现更多重复项。
Conclusion
我们开发了一个随机模型,用于根据 GossipSub 网络的 mesh degree 和整体大小来近似其直径。将此模型应用于以太坊网络显示 GossipSub 直径为 7。在此分析过程中,我们还观察到绝大多数重复消息是在第五轮和第六轮发送的,这与大多数节点刚刚被感染但剩余目标更少的时间段相吻合。
- 原文链接: ethresear.ch/t/gossipsub...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊 2026年协议级更新确定 3 大方向 82 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 69 浏览
- 如何去中心化构建区块? 252 浏览
- Builder Codes & ERC-8021:修复链上归属问题 290 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 315 浏览
- “夺旗”竞赛继续! 270 浏览
- EVM Gas 分析:新的执行跟踪数据 284 浏览
- 质押和链上信贷市场之间的微妙张力 385 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 336 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 283 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 398 浏览
- Vitalik: 重新评估以太坊 Layer2 384 浏览


