DAS分叉选择 - 共识
- 以太坊中文
- 发布于 2024-05-18 13:11
- 阅读 876
本文深入探讨了在引入数据可用性采样(DAS)后,分叉选择与数据可用性层之间的交互,旨在缓解潜在的攻击。文章首先识别了当前分叉选择规范下的潜在攻击,并提出了应对策略。此外,还讨论了紧密分叉选择、尾随分叉选择以及相关的攻击,并提出了(block, slot)分叉选择以及多数分叉选择来解决这些问题。
由 Francesco, Luca 和 Roberto 撰写
本文档的目标是加深我们对引入数据可用性抽样(DAS)后,分叉选择与数据可用性层之间交互的理解,旨在减轻可能出现的潜在攻击。为了实现这一目标,我们首先识别当前分叉选择规范下的潜在攻击,并提出应对它们的策略。此分析假设读者熟悉当前的分叉选择和已知攻击,以及PeerDAS。
分发阶段和抽样阶段
回顾一下,在 PeerDas 中,每个 blob 都会被单独水平扩展,垂直堆叠,并细分为 NUM_COLUMNS 列,这些列被用作抽样单元。PeerDas 包含两个阶段:一个分发阶段和一个抽样阶段。在分发阶段,列被分配给验证者的子集,每个子集负责保管一列或多列(CUSTODY_REQUIREMENT)。随后,在抽样阶段,验证者请求样本以验证数据可用性。这些样本或列,通过请求/响应机制从对等节点获取。如果验证者需要保管的所有列都可用,即使在完成实际抽样阶段之前,分发阶段也可以作为一种初步抽样阶段,使验证者能够认为数据可用。当使用后续分叉选择函数时,这被证明特别有价值,下面将进一步解释这个概念。
严格的分叉选择
理想情况下,几乎所有诚实验证者只会投票给完全可用的区块,而无需下载所有数据。为了实现这一点,我们可以要求在投票给一个块之前完成足够数量的抽样。我们将此称为严格的分叉选择。在 PeerDAS 中,这意味着验证者需要在收到一个块后立即执行对等抽样,并且在未完成之前不能投票给它。这给了我们一个有用的属性,我们称之为抽样的 \delta-安全性,对于一些依赖于抽样量的 \delta \in [0,1/2] (\delta 随着样本数量的增加而减小到 0):
抽样的\delta-安全性:如果某些数据的可用性低于一半,那么最多只有 \delta 比例的诚实验证者会认为它是可用的。因此,不会有超过 \delta 比例的诚实验证者会投票给一个不可用的块。
后续分叉选择
但是,为了避免在区块和列的分发与投票之间增加额外的步骤,人们可能会考虑放宽此要求,目的是将对等抽样从关键路径中移除。具体来说,有人提出,并且仍在讨论中,验证者可以放弃在对当前提议的区块进行投票之前完成对等抽样过程,并将其推迟到下一个插槽(甚至更远的将来)。相反,他们将根据列分发的结果来投票;如果其分配的子网内的所有数据都可用,则验证者认为整个块可用并相应地投票。然后,只有在下一个插槽之前才需要完成此块的对等抽样。我们将此称为后续分叉选择。
使用后续分叉选择并不一定意味着完全放弃抽样的 \delta-安全性,即使在“后续期间”也是如此。实际上,在列分发阶段包含足够数量的子网抽样使我们能够保持一定程度的\delta-安全性。在实践中,我们将进行比对等抽样更少的子网抽样,因为由于它产生的 gossip 放大因子,子网抽样对带宽的要求更高。因此,来自子网抽样的 \delta-安全性将适用于更高的\delta,这意味着更高比例的诚实验证者可能会被欺骗而做出错误的投票。
在本文档的其余部分讨论后续分叉选择时,我们将使用 \delta_p 来表示对等抽样的\delta-安全性,并使用 \delta_s 表示子网抽样的\delta-安全性。我们还将假设 \delta_s \gg \delta_p,即,与子网抽样相比,对等抽样的安全损失可以忽略不计。
攻击
回顾:事前重组
事前重组攻击是当前以太坊共识协议中一个众所周知的威胁。控制大量验证者的攻击者可以通过战略性地扣留区块来影响区块链的规范链。在这种攻击中,攻击者私下构造区块,并在多个插槽中精心策划其验证者之间的投票,最终在诚实区块发布时胜过它们。这可以通过在适当的时候发布扣留的区块和证明来克服提议者激励,或者通过直接克服诚实验证者的投票来实现。
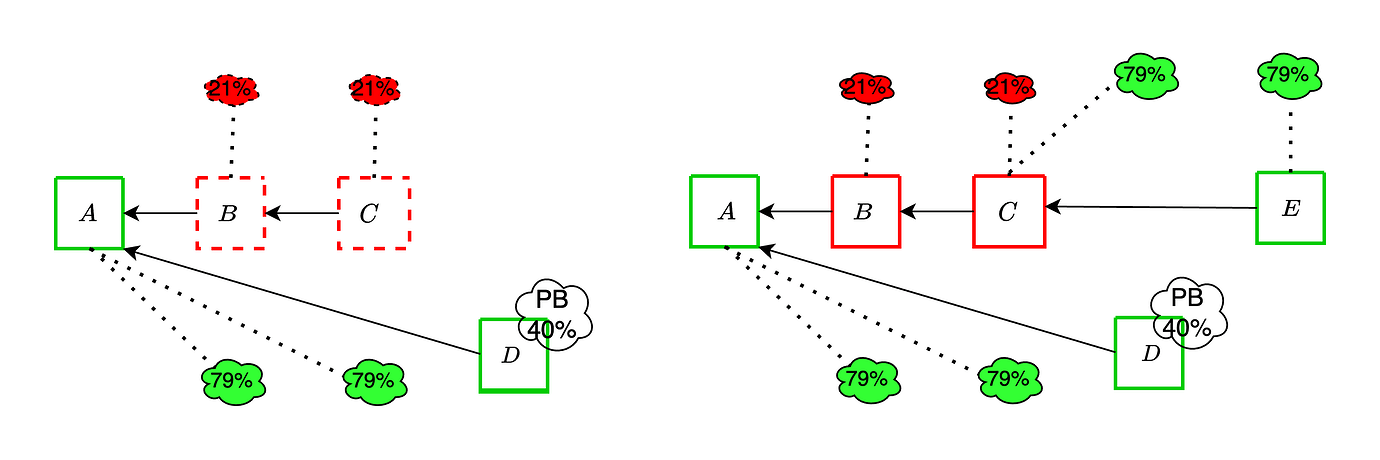
我们现在展示前一种策略的一个实例,其中敌对区块 B 和 C 与敌对证明一起被扣留,每个证明占每个委员会的 21%。诚实的提议者用区块 D 扩展区块 A,然后攻击者在证明截止日期之前揭示被扣留的对象。由于敌对投票超过了提议者激励,因此诚实的区块没有被投票并被孤立。
即使添加了 DAS,这些攻击仍然可行,事实上,由于我们将在后续章节中讨论,这些攻击可能会变得更加有效。
提议者看到不可用,证明者看到可用:增强的事前重组
使用严格的分叉选择
攻击者可以通过利用 \delta 比例的诚实验证者来稍微加强前一节中的事前重组攻击,这些验证者可能会被欺骗,认为不可用的区块是可用的。攻击者按以下步骤进行:
- 攻击者不完全扣留区块 B,而是发布它,但不完全发布相关数据。这样做是为了最大化子网抽样成功的诚实验证者的数量,从而认为 B 是可用的。
- 因此,\delta 个这样的验证者投票给 B,加入 \beta 个敌对验证者。
- 然后,攻击者用另一个完全可用的区块 C 扩展 B。同样,\delta 个诚实验证者和 \beta 个敌对验证者投票给 C。
- 这种情况一直持续到一个诚实的插槽,其提议者试图分叉出 B(除非他们碰巧在认为其可用的 \delta 中)。此时,攻击者使 B 可用,如果敌对链上的投票超过提议者激励,则诚实的提议将不会被投票。
与之前的攻击相比,攻击者每个插槽额外获得\delta。因此,重要的是进行足够的抽样以保持\delta 较低。
使用后续分叉选择
如前所述,这里我们将假设 \delta_p \ll \delta_s 并且只关心 \delta_s 的影响。攻击者只能在后续期间利用 \delta_s 。如果后续期间为一个插槽,则它最多可以向其攻击预算添加一个 \delta_s 。
这种攻击表明需要进行足够的子网抽样,以使事前重组攻击不会变得过于容易。例如,如果 \delta_s 为 20%,则一个 10% 的攻击者每天可以进行大约 100 次这样的重组,而不是每天大约一次。更糟糕的是,使用 PeerDAS 规范的当前参数,控制单个提议者的攻击者可以执行重组!这是因为 CUSTODY_REQUIREMENT,验证者参与的最小子网数,设置为 1,这使得 \delta_s 接近 50%。例如,攻击者可以在 32 个子网中的 15 个子网中提供数据,并说服这些子网中的所有验证者投票给他们的不可用区块,从而克服提议者激励。
缓解
正如此处已经讨论过的,可以通过在插槽 n 中的 10 秒内完成对等采样的插槽 n+1 的证明者来缓解此攻击向量,而提议者可以继续尝试采样直到他们提出。如果提议者扩展了证明者认为不可用的区块,他们会尝试再次采样。这在精神上很像 view-merge,但不需要提议中的任何额外消息。在先前描述的攻击中,这种缓解措施将使插槽 4 的证明者不会将 B 视为可用除非 D 的提议者也这样做:要么提议者认为 B 可用并且 D 扩展 C,要么提议者认为 B 不可用并且证明者也这样做。在任何一种情况下,他们都会投票给 D。
这种缓解措施的缺点是会使围绕对等采样的时序假设恶化,从而降低后续分叉选择的好处。尽管如此,如果这是由 DAS 引起的唯一分叉选择问题,我们可能会乐于这样解决它,并在其他方面保持原样。下一个攻击似乎没有如此简单的缓解措施,并促使我们希望转向 (区块, 插槽) 分叉选择,以更有效地解决与(不可用)可用性相关的攻击向量。
提议者看到可用,证明者看到不可用
目标数据发布
该攻击将依赖于能够说服一个诚实的提议者,即使在他对其执行对等采样之后,不可用的区块也是可用的。这种假设有多么现实取决于对等采样是如何执行的。例如,假设抽样查询失败的节点只是尝试与其他对等节点重新查询。然后,如果攻击者想要针对特定提议者,它必须:
- 将提议者的验证者身份链接到一个节点
- 确保它控制着该节点的至少一个对等节点,并声明它保管着所有列
- 使所有数据不可用
- 在该节点与其他对等节点失败后,等待该节点向其控制的对等节点发送抽样查询,并答复所有这些查询。
欺骗诚实的提议者以扩展不可用的链
考虑到这种能力,攻击者可以操纵诚实的提议者扩展不可用的链,从而导致他们的区块被重组。在这种情况下,我们仅假设攻击者控制两个连续的提议者,在这种情况下分别是插槽 2 和插槽 3 的提议者。事件的顺序如下:
- 攻击者仅在插槽 2 中发布一个不可用的区块 B,并且不在插槽 3 中发布任何区块。
-
重要的是,攻击者说服插槽 4 的提议者 B 是可用的。结果,插槽 4 的提议者没有尝试通过以下原因通过提议者激励重组来重组 B:
- 提议者认为 B 是可用的。
- 即使 B 没有收到任何投票,提议者激励重组机制目前也不会尝试跨越多个插槽的重组(作为活跃性保护)。
- 因此:
- 由于所有其他验证者都认为 B 是不可用的,因此他们继续投票给 A。
- 插槽 5 的提议者使用 D 扩展 A,从而有效地重组诚实且可用的区块 C。
攻击甚至可以连续针对多个诚实提议者,从而导致他们所有的区块都被孤立!鉴于攻击者不需要控制大量的权益就可以完成这一攻击,因此这尤其严重。
(区块, 插槽) 分叉选择
通过采用一种被称为 (区块, 插槽) 分叉选择规则的变体,可以有效地解决上述讨论的攻击。这种修改是几年前提出的,专门用于考虑与空插槽关联的证明。在任何给定的插槽 t 中,考虑到提议 B 扩展了规范链 A 的头,我们还考虑由 A 标识的空插槽。为了清楚起见,通过此修改,我们将对区块 A 的投票视为对 (区块, 插槽) 对的投票(而不仅仅是对区块 A 的投票)。
在上图中,我们展示了当前分叉选择(左)和 (区块, 插槽) 分叉选择(右)之间的区别,在一个区块 B 被提议有点晚的情况下。从本质上讲,这种方法使我们能够在插槽 t+1 中同时考虑 (B,t+1) 和 (A,t+1)。正如我们将在下面展示的,这有效地缓解了先前讨论的攻击。
重新审视最后的攻击
考虑以下场景(这是提议者看到可用,证明者看到不可用攻击的起点):
- 区块 A 是分配给插槽 t 的完全可用的区块。
- 另一方面,区块 B 是不可用的,但由于敌对操纵,对于少数验证者来说显得可用。
按照当前的分叉选择函数,在插槽 t+1 期间:
- 大多数验证者认识到 B 是不可用的,因此投票给 A。
- 少数验证者将他们的投票投给 B。
通过引入 (区块, 插槽) 分叉选择函数,大多数验证者将有效地投票给(A,t+1)对。
继续攻击中的事件序列,在插槽 t+2 中,攻击者放弃提出任何区块。因此,大多数验证者将选择投票给 A,这实际上意味着投票给(A,t+2)对。
此时,尽管攻击者使插槽 t+3 的诚实提议者相信 B 是可用的,但由于链(A,t+2)比头部为(B,t+1)的链更重,因此提议者仍会扩展 A。
(区块, 插槽) 规范
获取由插槽 t 的区块提议者提出的区块 A,以及在插槽 t+d 中对区块 A 投票 v。然后,v 被认为是对任何元组\{(A,t),(A,t+1),\cdots,(A,t+d)\}的投票,因为 v 声明规范链的头在所有这些插槽中都是 A。
因此,分叉选择函数还通过 (区块, 插槽) 而不是仅仅通过区块来进行。
具体来说,(A,t) 的子节点是所有那些 (区块, 插槽) 对 (B,t+1),其中 B 要么是 A,要么是 A 的子节点。这意味着在这种情况下,(A,t+1) 被视为 (A,t) 的子节点。因此,对 A 的任何子节点的支持现在都与对空插槽(A, t+1) 的支持进行比较。分叉选择以这种方式进行,直到到达当前插槽,此时,它输出头(区块,插槽)对的区块。请注意,通过我们定义事物的方式,对对 (A,t+d) 的支持包括对祖先为 A 且提议的插槽高于 t+d 的任何区块 C 的所有投票,但该链不包括在插槽 t+d 中提议的任何区块。
我们在下图中说明了这一点。左边是带有证明的实际区块树。右边是运行分叉选择时解释的区块树。在插槽 t+1 中,选择是在 (B,t+1) 和 (A,t+1) 之间,而后者的权重由插槽 \ge t+1 中对 A 的证明(绿色和橙色)以及插槽 t+2 中对 C 的证明(黄色)组成,因为这些也表明 A 是插槽 t+1 中的头。
此处 尝试了一个简单的 (区块, 插槽) 分叉选择规范的早期尝试。get_head 中的循环被修改为按插槽进行。在每个插槽中,head 的最重的子节点 best_child 都与 empty_slot_weight 进行比较,empty_slot_weight 是“以空插槽为根的子树”的权重,通过如上所述解释投票由 get_empty_slot_weight 计算。我们在此处包含修改后的 get_head 和 get_empty_slot_weight 的重要部分(在这两种情况下,除了删除与退避逻辑相关的部分,我们将在后面讨论)。
def get_head(store: Store) -> Root:
# 获取仅包含可行分支的过滤区块树
blocks = get_filtered_block_tree(store)
# 执行 LMD-GHOST 分叉选择
head = store.justified_checkpoint.root
slot = Slot(blocks[head].slot + 1)
while slot <= get_current_slot(store):
children = [\
root for root in blocks.keys()\
if (blocks[root].parent_root == head\
and blocks[root].slot == slot)\
]
if len(children) > 0:
best_child = max(children, key=lambda root: (get_weight(store, root), root))
best_child_weight = get_weight(store, best_child)
empty_slot_weight = get_empty_slot_weight(store, head, slot)
if best_child_weight >= empty_slot_weight:
head = best_child
slot = Slot(slot + 1)
return head
def get_empty_slot_weight(store: Store,
root: Root,
slot: Slot) -> Gwei:
...
attestation_score = Gwei(sum(
state.validators[i].effective_balance for i in unslashed_and_active_indices
if (i in store.latest_messages
and i not in store.equivocating_indices
and (
(store.latest_messages[i].root == root
and store.latest_messages[i].slot >= slot
or (store.latest_messages[i].slot > slot
and not store.latest_messages[i].root == root
and get_ancestor(store, store.latest_messages[i].root, slot) == root
)
))))
...
return attestation_score + proposer_score
退避方案
当前提案的一个缺点是,在不良网络条件下的性能会变差。如果区块延迟 > SECONDS_PER_SLOT / 3(在当前配置中为 4 秒),则链增长将完全停止。
因此,需要一种退避方案,以在扩展延迟期间促进链的进展。如果没有这种机制,链将持续构建在同一个(空)区块上,从而导致一系列空区块并且无法使用非空区块扩展链。
退避方案旨在缓解链中长时间的空区块。当发生此类实例时,该方案通过协助潜在的非空区块积累必要的证明来介入。随着这些受支持的区块成功地推进链,退避机制将逐渐停用。这种逐渐停用的过程一直持续到系统达到不再需要退避机制的状态。
退避机制的激活和停用由 backoff_status 表示,该状态在 get_head 中创建和更新。至关重要的是,如果两个诚实验证者在执行 get_head 时处于同一路径上,他们将共享相同的退避状态。这意味着,在同步下,对于选择区块树相同分支的诚实验证者,退避机制是同步的,同时激活和停用。在上面链接的规范中,活动的退避会使空插槽的投票计数延迟一个插槽:A 的投票只有在至少来自插槽 s+1 的情况下才计入空插槽(A,s)。换句话说,我们获取所有直接对空插槽的投票,并将它们向后移动一个插槽:对 (A,t+1) 的投票计入 (A,t),对 (A,t+2) 的投票计入 (A,t+1) 等等。例如,看一下绿色证明,它们在插槽 t+1 中投票给 A。当退避未激活时,这些会为 (A,t+1) 贡献权重(更准确地说,在插槽 t+1 中运行时被 get_empty_slot_weight 计数,A 是 head),但是当退避激活时,它们会回到仅为 (A,t) 贡献。同样,橙色证明到 (A,t+2),当退避激活时,它们仅为 (A,t+1) 贡献。
在下图中,网络延迟很高,并且所有区块提议都延迟了几秒钟,因此它们永远不会获得任何投票。起初,这导致 B 被孤立,因为所有投票都投给了 (A,t+1)。为简单起见,我们假设退避立即在该分支上激活。在插槽 t+2 中,C 也较晚,并且所有投票再次投给 A。由于退避已经激活,因此这些投票不计入 (A,t+2) 而仅计入 (A,t+1),因此 C 仍然是链的头,并在下一个插槽中投票。同样,由于退避已激活,因此这些投票仅计入 (C,t+2) 而不计入 (C,t+3),即,它们不会“反对”在插槽 t+3 提出的区块 D。为了使区块被孤立,现在需要延迟整整一个插槽:插槽 t+3 上对 A 的投票将计入 (A,t+2),因此与 C 对立,但是只要 C 在插槽 t+3 之前到达,就不会有这样的投票。
激活退避状态的具体机制仍在进行中,到时将所有相关逻辑都限制在 update_backoff_status 中,该函数在 get_head 循环的每次迭代结束时调用。
使用 (区块, 插槽) 攻击 DAS 分叉选择
通过采用 (区块, 插槽) 分叉选择函数,如果在证明截止日期之前区块不可用,则大多数诚实验证者将不投票给它。相反,他们将投票给空区块。有了这个,我们希望实现比抽样的 \delta-安全性更强的属性:
如果验证者集 > \frac{1}{2(1-\delta)} 诚实且网络同步,则没有不可用的区块位于任何诚实验证的规范链中
推理看起来很简单:如果在运行分叉选择时,区块 B 在给定的时间不可用,则抽样的 \delta-安全性可确保任何先前插槽的委员会中最多有 \delta 比例的诚实验证者可能已经投票给了它。特别是,B 的提议插槽的至少 1-\delta 诚实验证者将投票给空插槽。如果 > \frac{1}{2(1-\delta)} 的验证者是诚实的,那么这是 > \frac{1}{2} 的验证者,并且空插槽将占多数并获胜。
不幸的是,事情实际上并非如此简单。 在上面,我们假设不投票给 B 的验证者将投票“支持空插槽”。实际上,如果有多个“空插槽”可以投票,例如由于平衡攻击而导致的链分裂(如左图所示),则可能会有多个“空插槽”。 然后,诚实的投票将在多个分支之间分配,并且不可用的区块对于已被诱骗将其视为可用的验证者仍然可以“看起来”是规范的。实现相同目的的另一种方法是用可用的区块来重复,并用不可用的区块来划分大多数诚实的投票,而不是让他们像下面的右图那样进入空区块。
进一步改进的方向:多数分叉选择
目前尚不清楚是否有可能使用“已知工具”完全消除此攻击向量(我们认为(区块, 插槽)分叉选择是这样的,因为它已经被讨论了多年,但尚未实现)。一个潜在的有希望的方向是做一些类似于(区块, 插槽)的事情,但甚至更极端:在 get_head 循环中的插槽 t 中,我们可以找到 best_child,然后将其与所有来自未在best_child 的子树上投票的插槽 \ge t 的投票权重进行比较。换句话说,我们需要来自插槽 t 的区块拥有来自插槽 \ge t 的所有证明权重的多数。这样,攻击者找到拆分诚实投票的方法都无关紧要:每当投票可能投给区块但没有时,该投票都是反对该区块的。
这将非常清楚地给我们以前希望得到的更强的属性,因为不可用的区块需要获得每个委员会权重的多数才能胜过空插槽。挑战在于确保这种更改不会以微妙的方式破坏其他任何东西,使已知攻击恶化或使停滞活跃度变得更加容易。
你可以在此处找到从先前的(区块, 插槽)规范到多数分叉选择的初步规范更改。重要的是,现在 get_empty_slot_weight 会计算所有可以位于 `best_child_root
- 原文链接: ethresear.ch/t/das-fork-...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 新帖子 – ImmuneBytes 47 浏览
- DeFi 介绍 - CoW DAO 10 浏览
- 以太坊 2026年协议级更新确定 3 大方向 94 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 75 浏览
- 后量子时代,我们如何保护隐私 120 浏览
- 为机器人募资:发展agent资本市场 199 浏览
- 如何去中心化构建区块? 259 浏览
- 区块链如何悄然保护你的在线购物体验 306 浏览
- Builder Codes & ERC-8021:修复链上归属问题 293 浏览
- MCP安全检查清单:AI Agent 的 24 项关键检查 214 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 324 浏览
- “夺旗”竞赛继续! 276 浏览

 \
3120×1040 145 KB
\
3120×1040 145 KB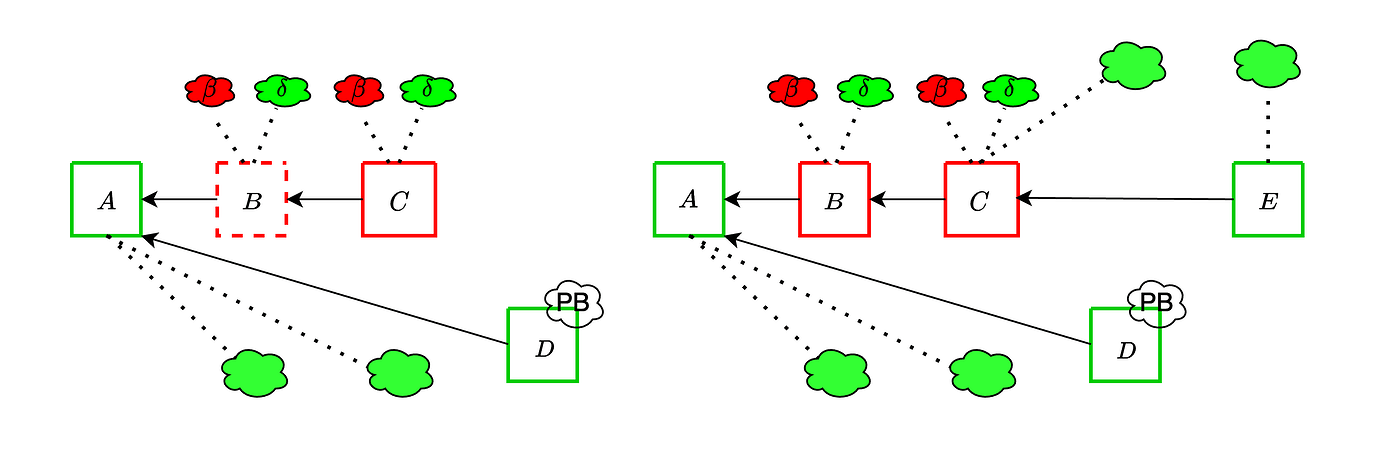 \
3036×1000 116 KB
\
3036×1000 116 KB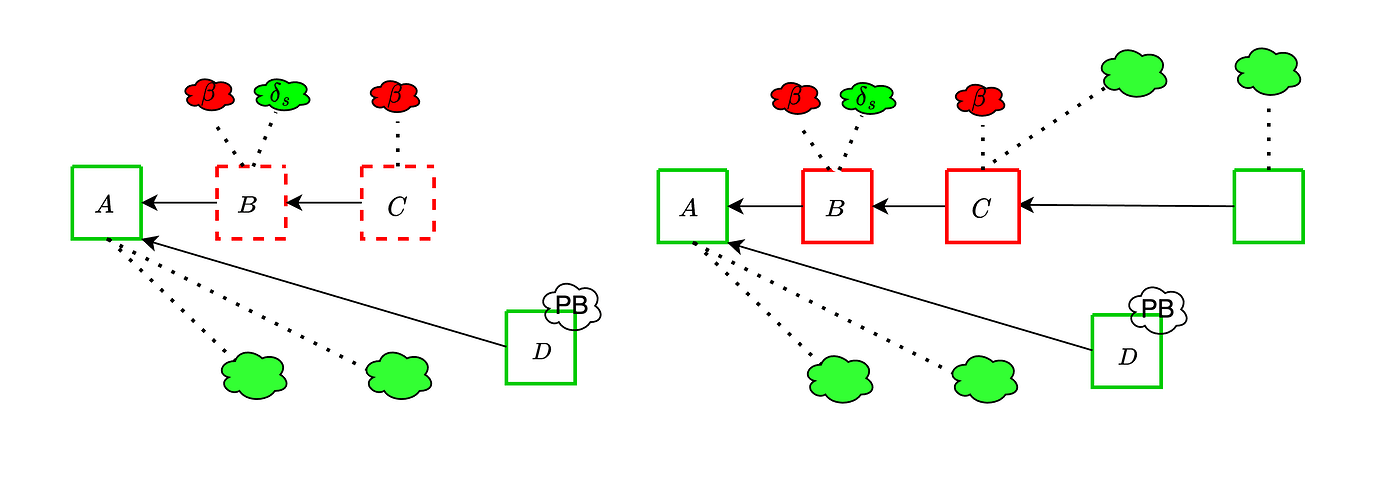 \
3052×1096 133 KB
\
3052×1096 133 KB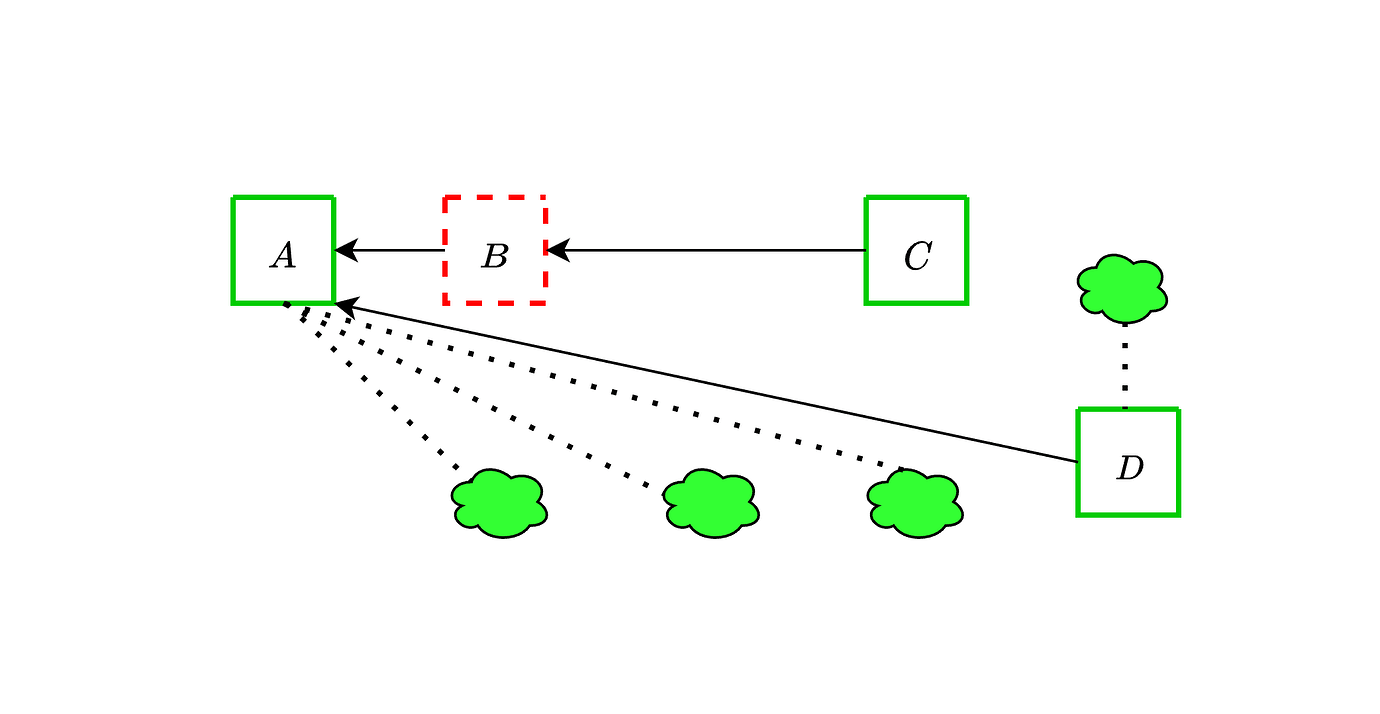 \
2084×1080 70.1 KB
\
2084×1080 70.1 KB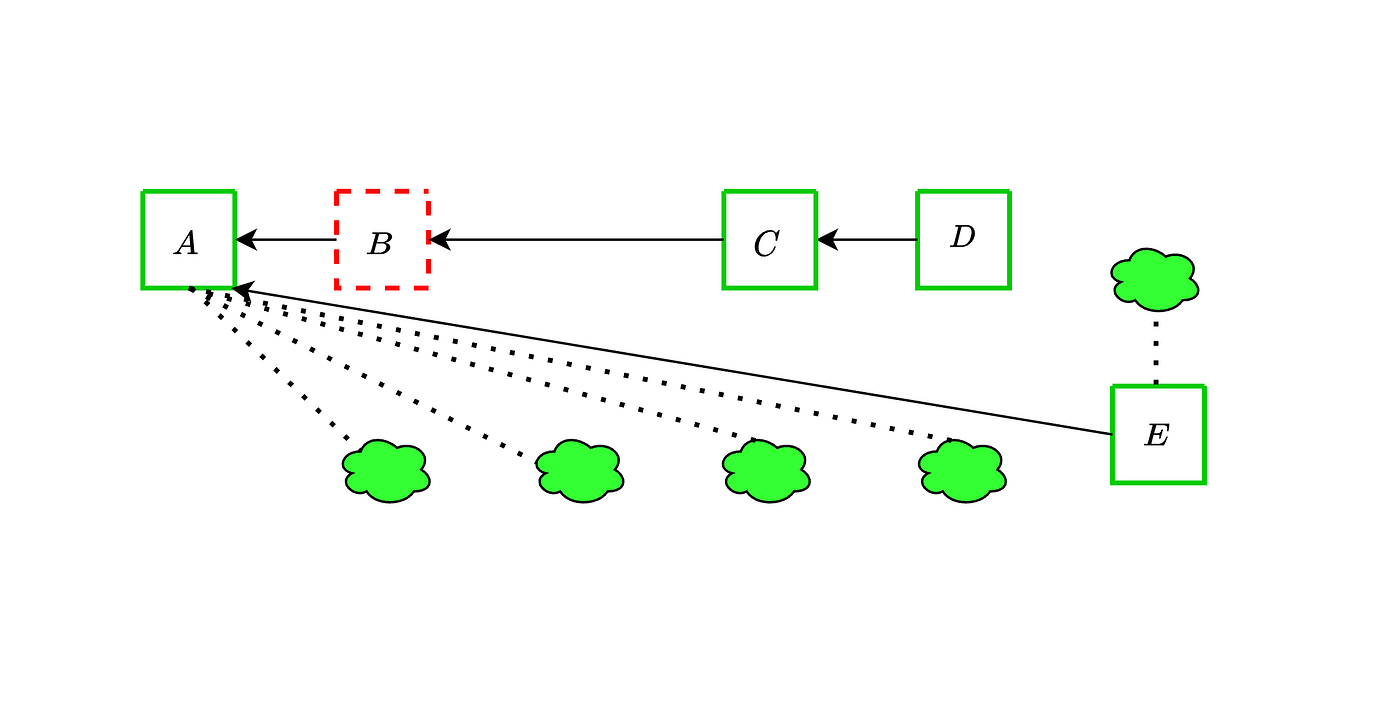 \
2280×1160 82.6 KB
\
2280×1160 82.6 KB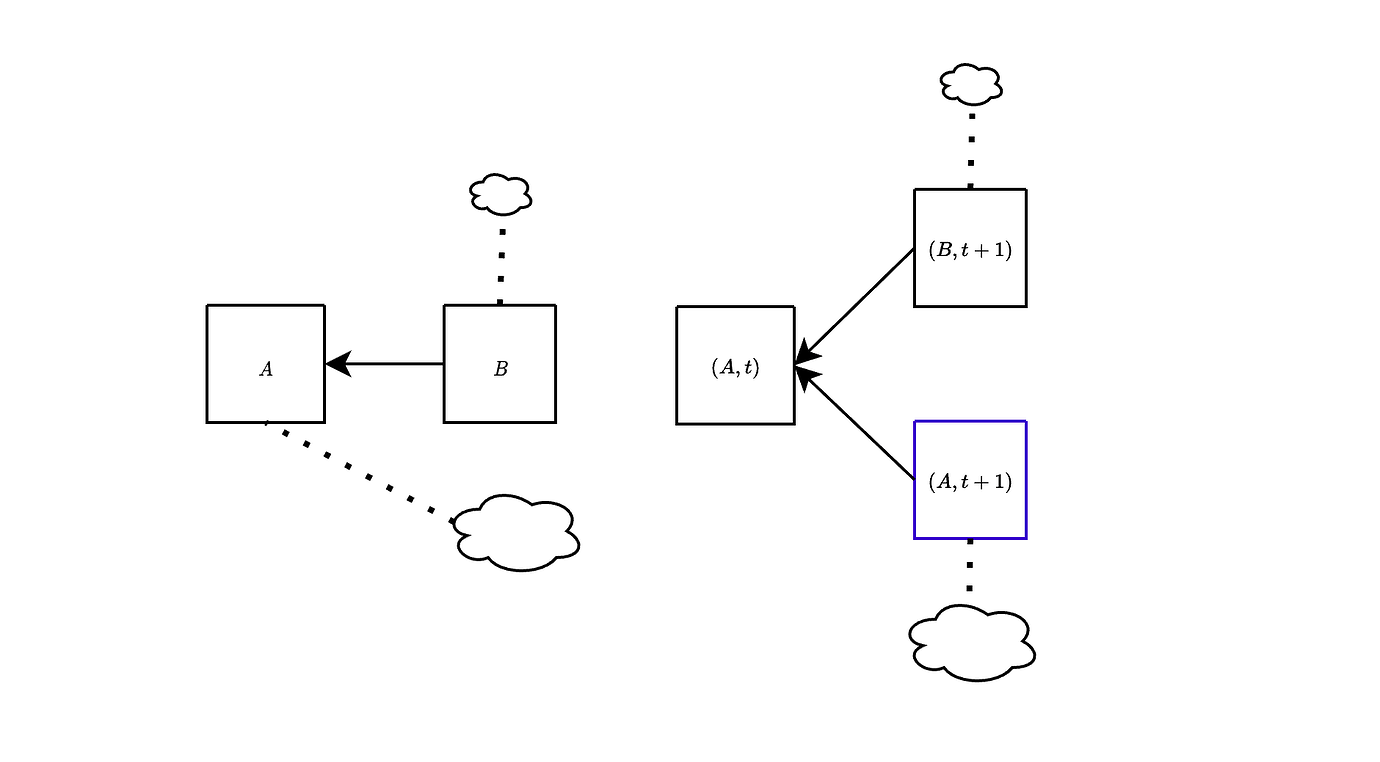 \
1880×1040 12.4 KB
\
1880×1040 12.4 KB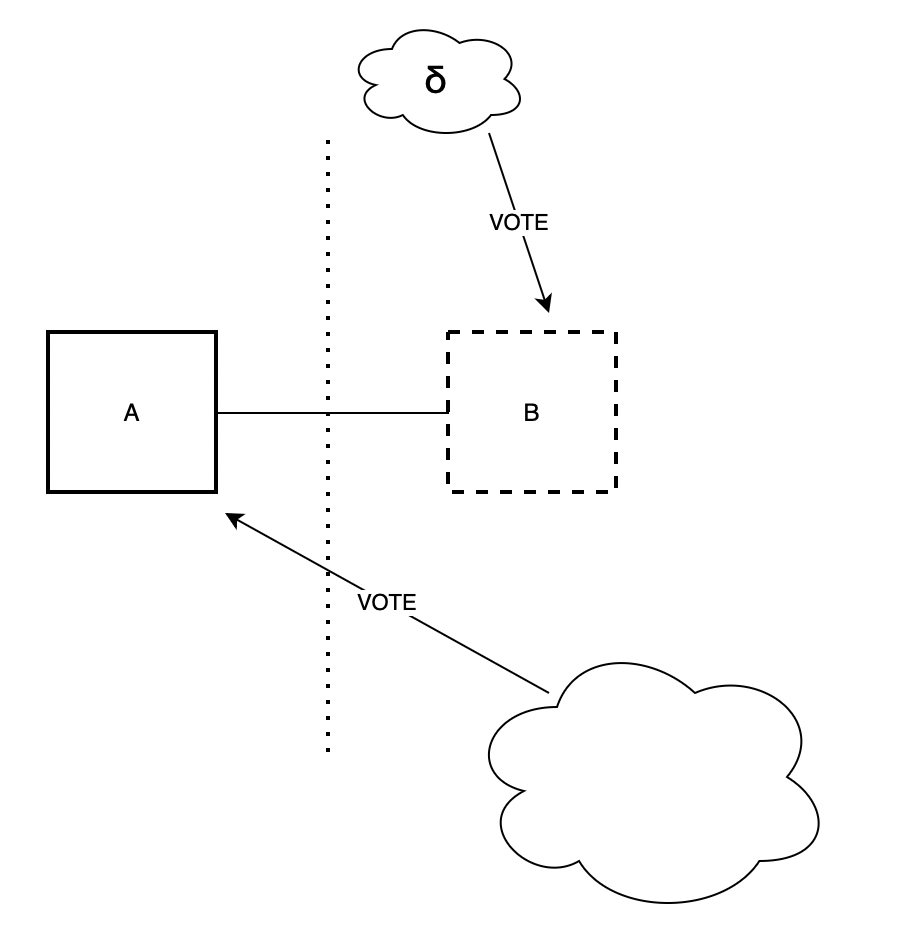 \
906×950 48.5 KB
\
906×950 48.5 KB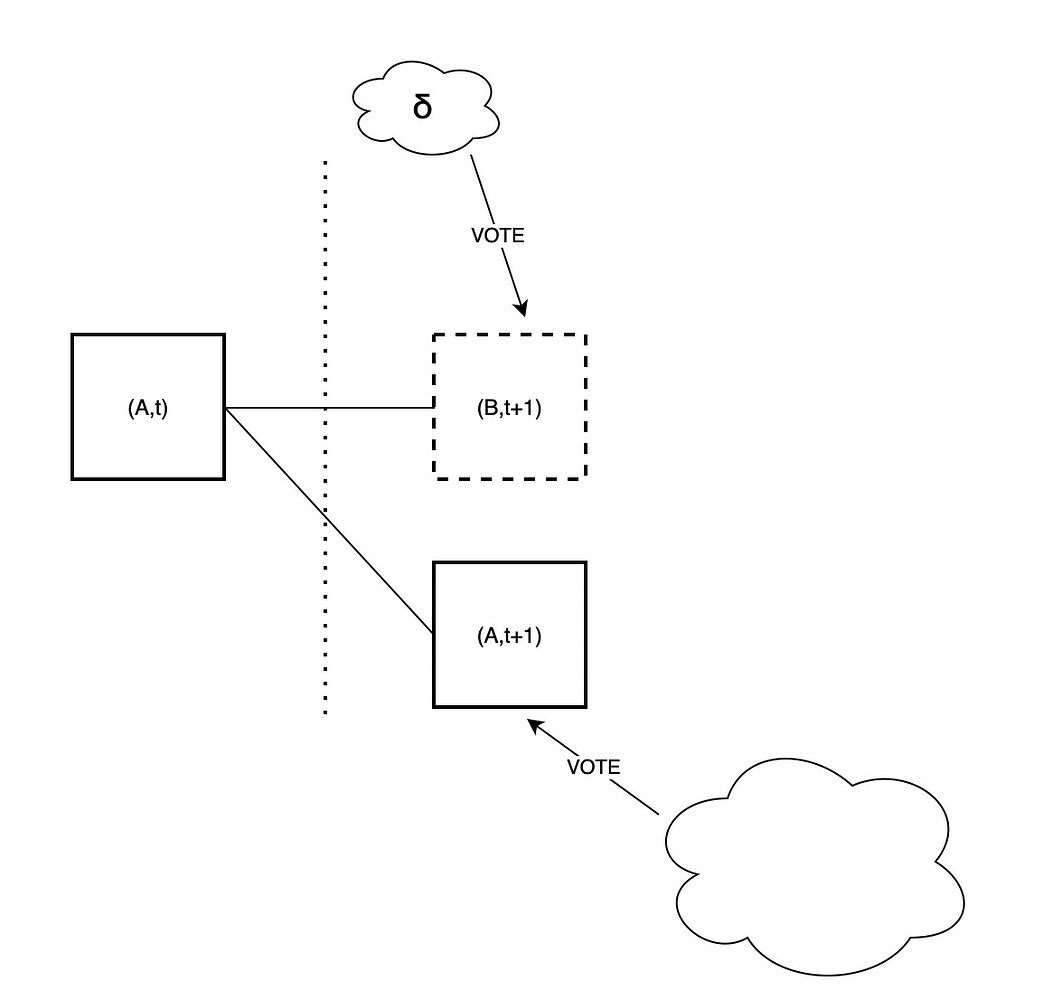 \
区块可用性图1154×1106 45.5 KB
\
区块可用性图1154×1106 45.5 KB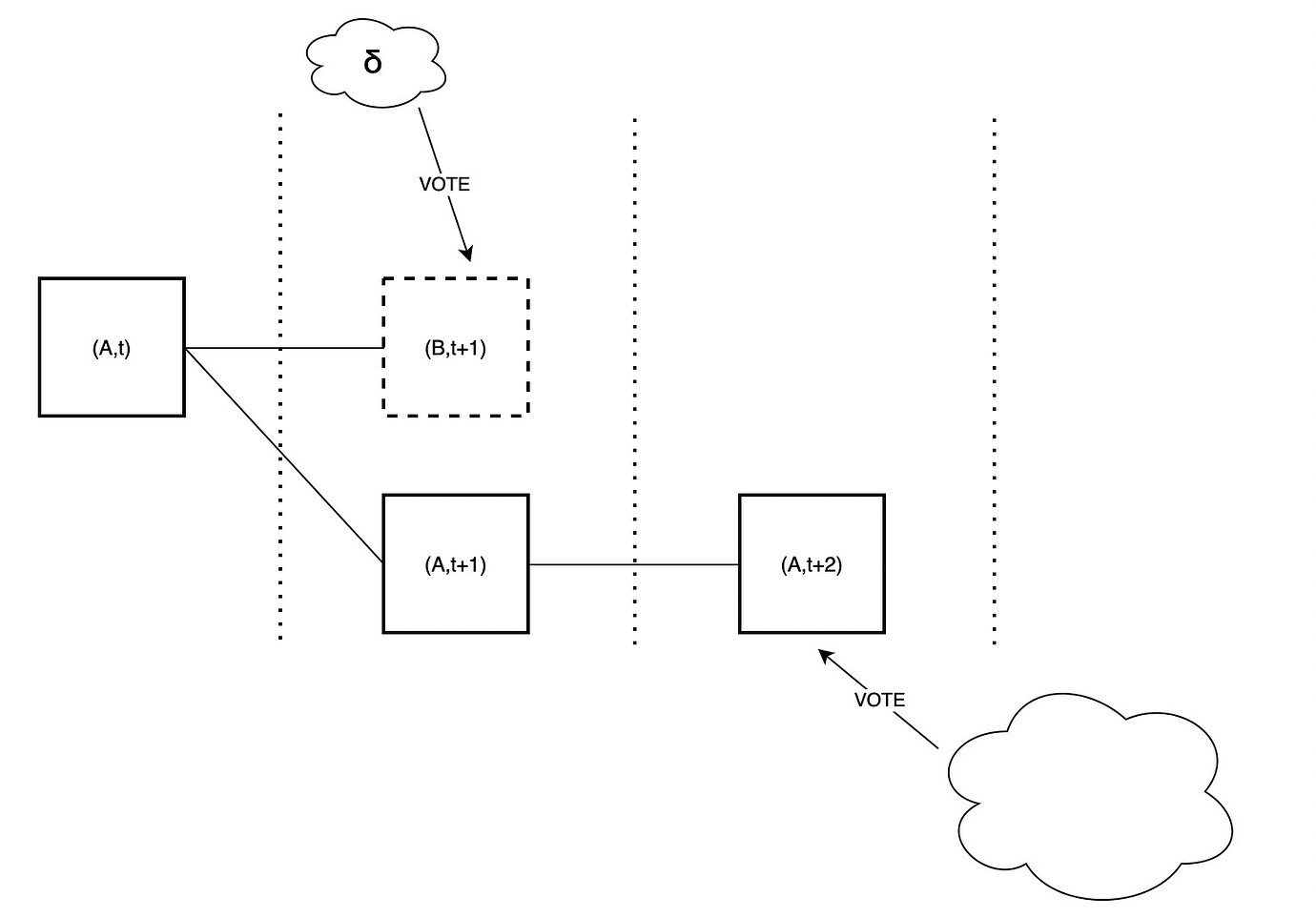 \
1530×1068 51.7 KB
\
1530×1068 51.7 KB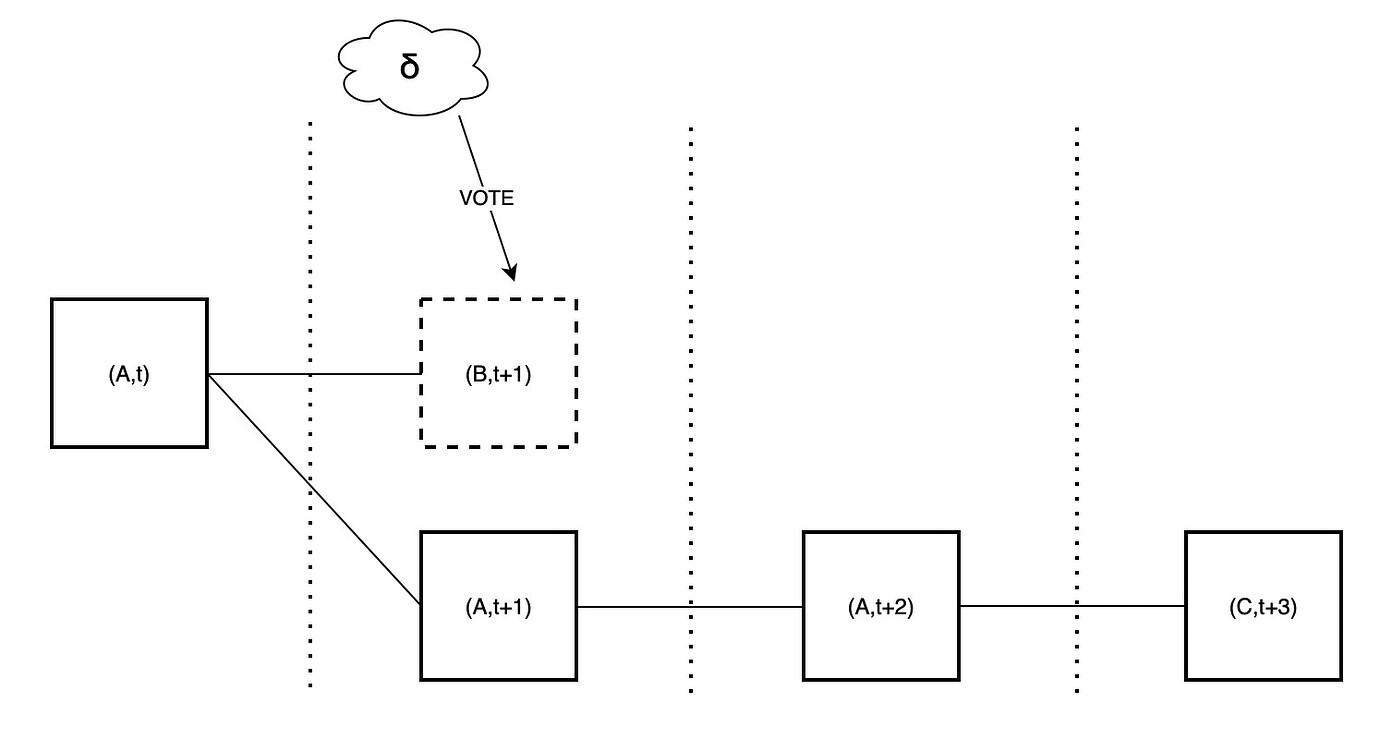 \
1494×800 44.4 KB
\
1494×800 44.4 KB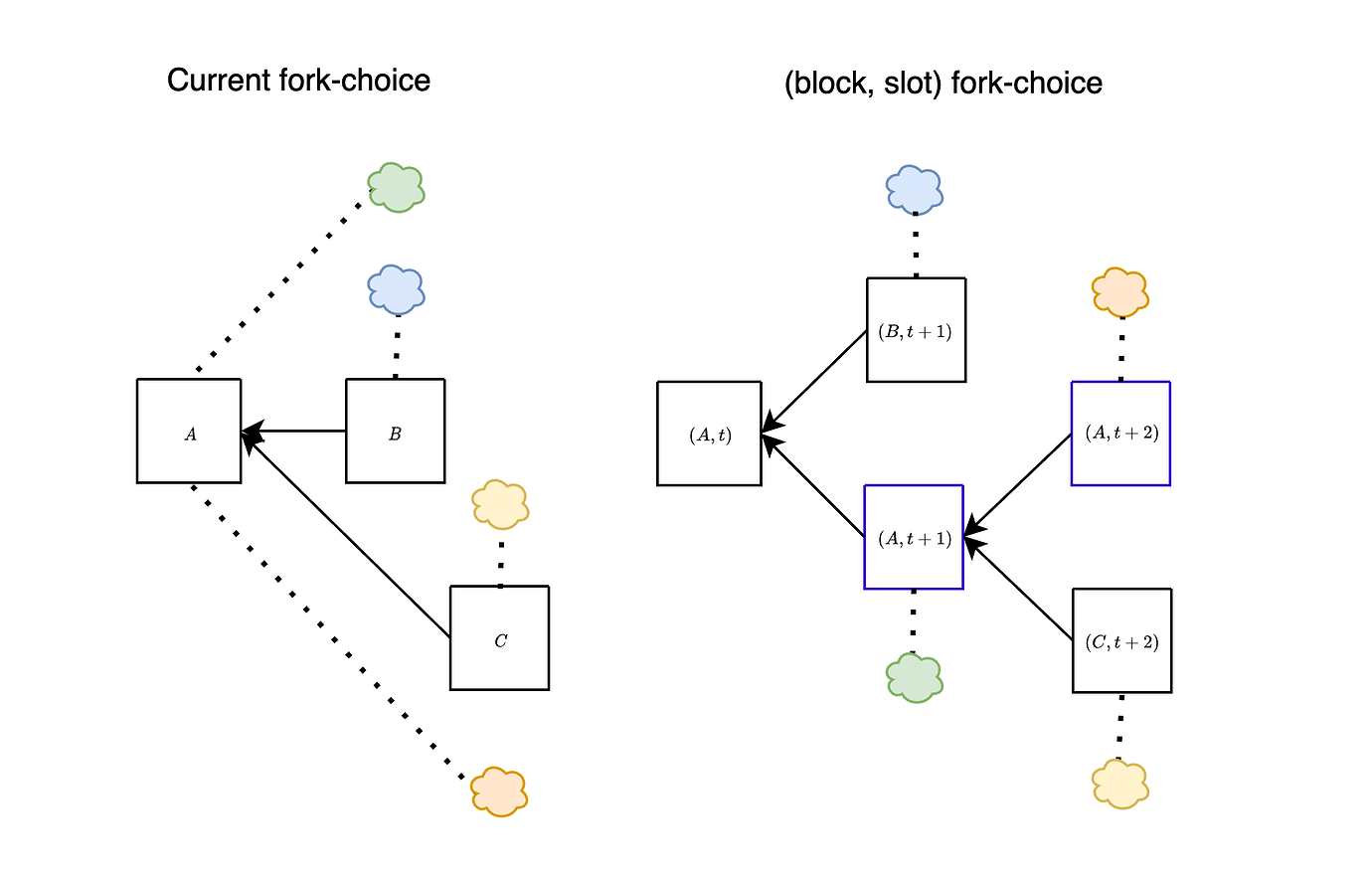 \
2120×1360 118 KB
\
2120×1360 118 KB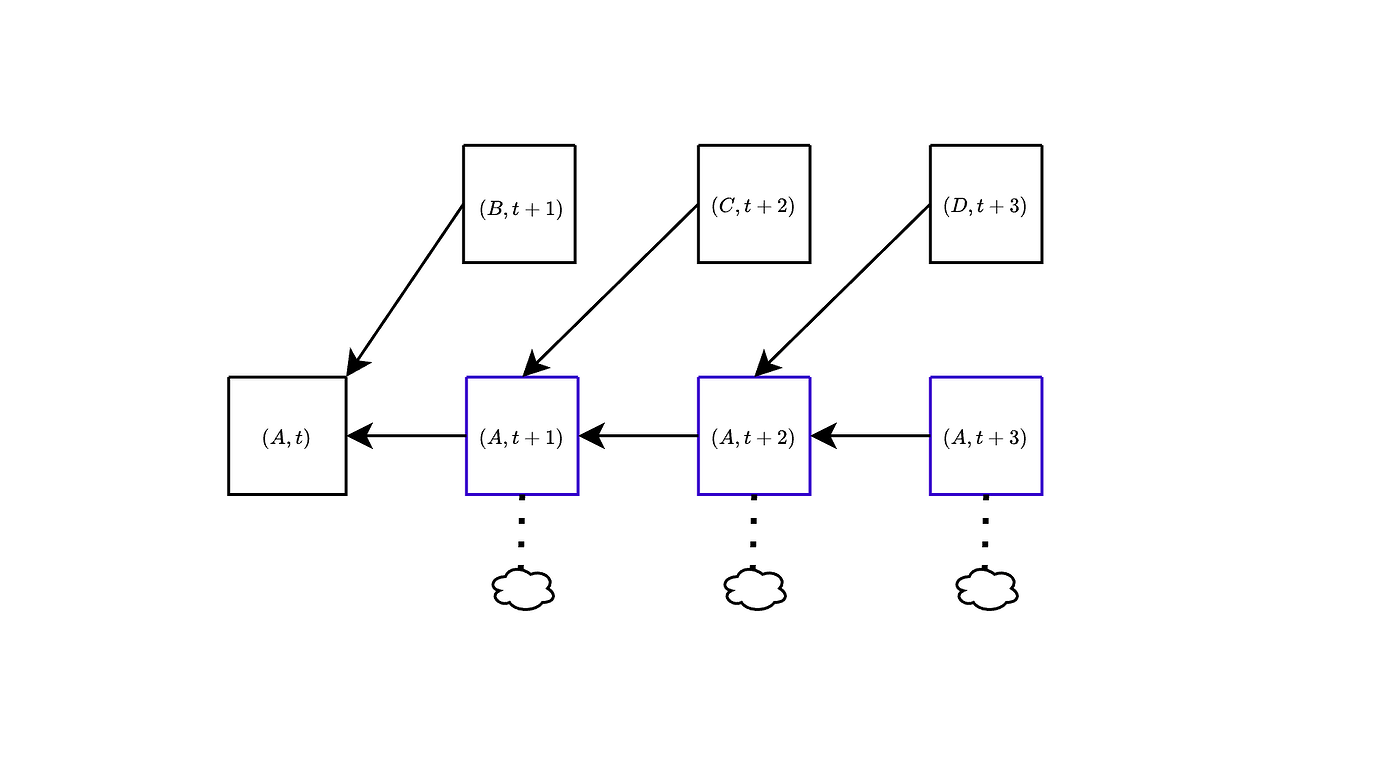 \
1880×1040 10.4 KB
\
1880×1040 10.4 KB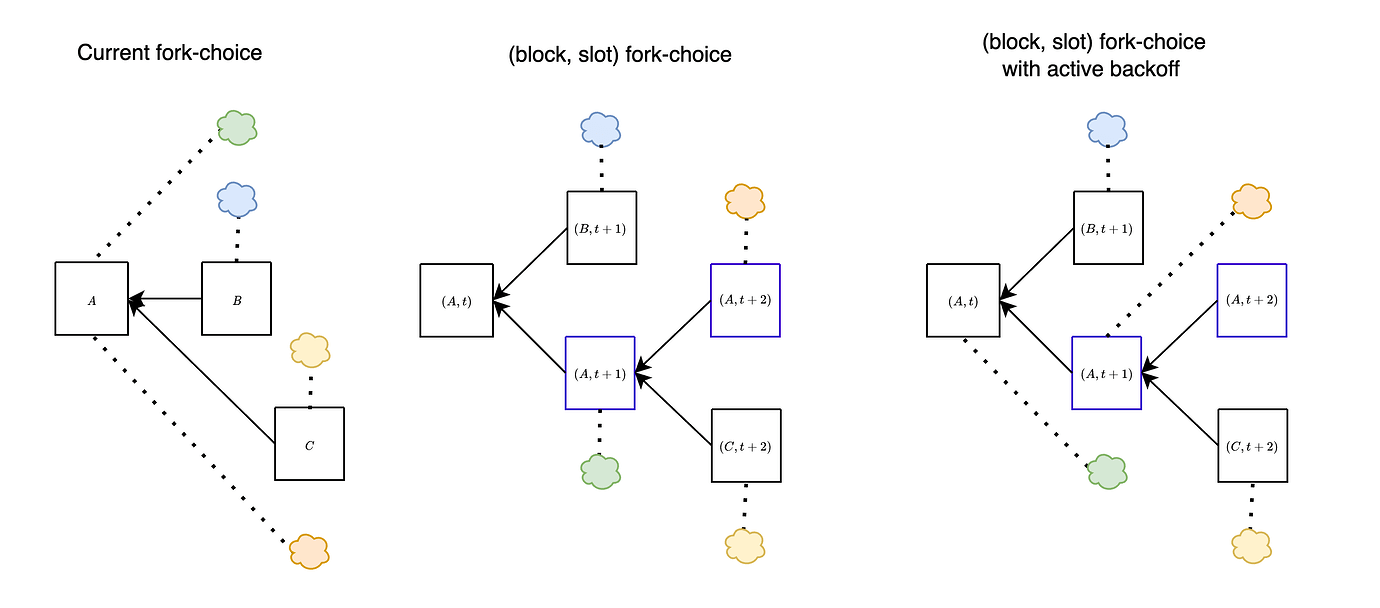 \
3040×1340 171 KB
\
3040×1340 171 KB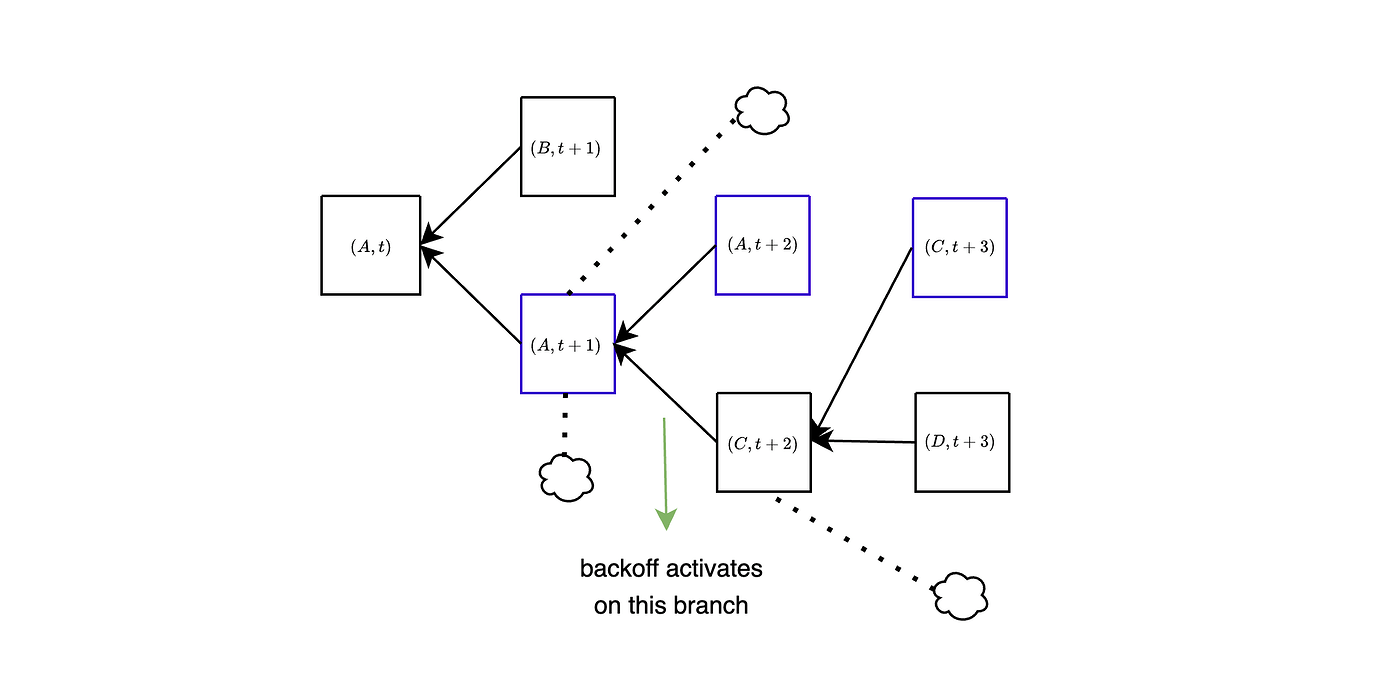 \
2240×1120 92.4 KB
\
2240×1120 92.4 KB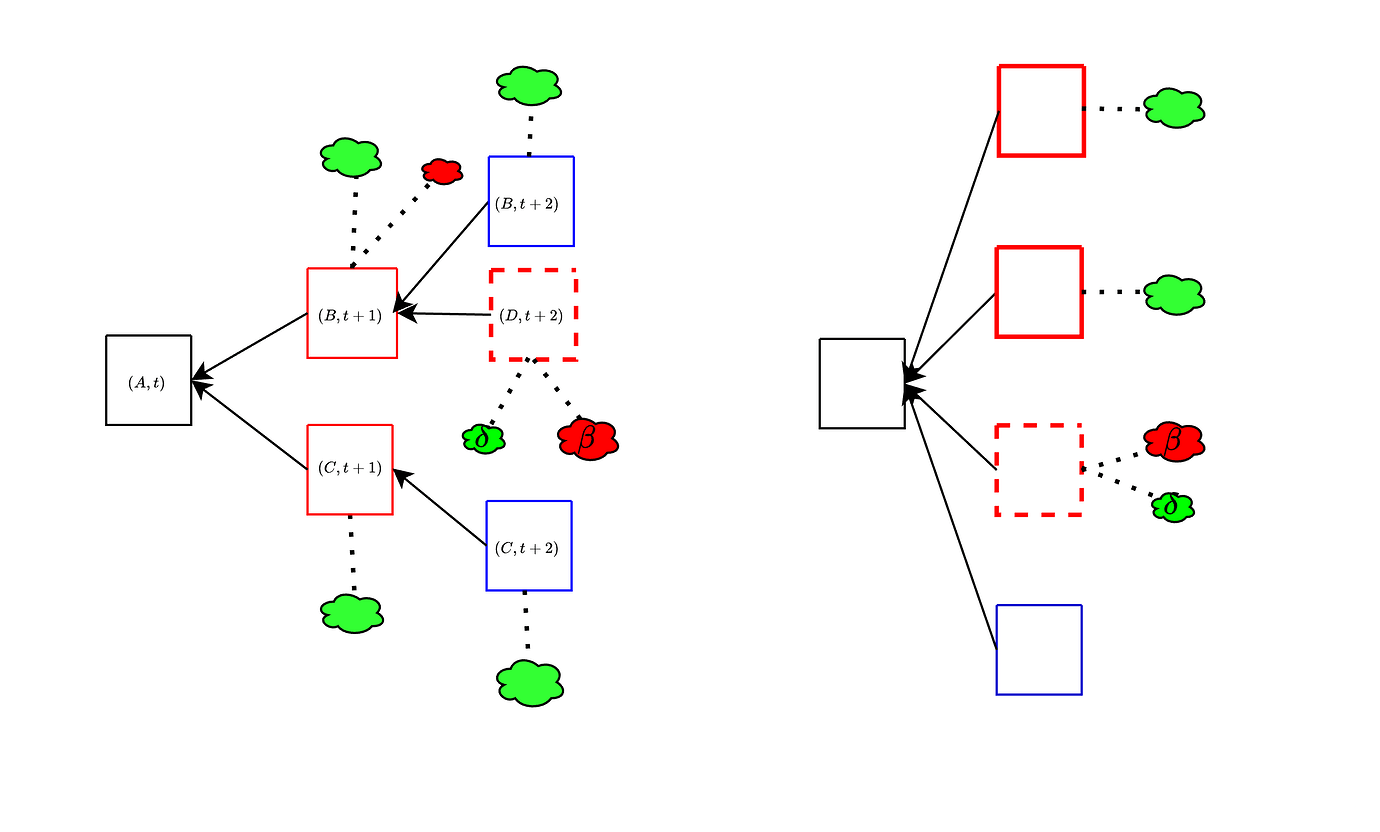 \
2468×1488 131 KB
\
2468×1488 131 KB
