Merkle Patricia Trie 简介

介绍

以太坊依赖于密码学数据结构来高效地存储和验证其状态。其中一种结构是 Merkle Patricia Trie (MPT)，它为以太坊的状态管理提供支持。在更深入地探索这个工具之后，很明显，MPT 是一种复杂的数据结构——远比简单的 Merkle 树复杂。这就是我们觉得创建这篇文章很重要的原因：让 MPT 更容易理解。在这里，我们将解释什么是 MPT，以太坊如何使用它以及它的证明如何工作。在即将发布的文章中，我们将解释如何对 MPT 进行算术化，以便生成证明，表明我们验证了元素是否在树中，或者树是否已成功更新。

在下面的内容中，我们仅假设你对 Merkle 树 和密码学哈希函数有基本的了解。

Merkle 树快速回顾

Merkle 树是一种二叉树，其中：

• 叶子节点 包含数据的哈希值。
• 非叶子节点 包含其子节点连接后的哈希值。
• 根哈希 充当所有叶子节点数据的密码学指纹。换句话说，它是一个短的、固定大小的摘要（哈希值），可以唯一地标识大量数据——就像一个唯一的签名。

Merkle 树用于 数据完整性证明：你可以通过提供 Merkle 路径（从叶子节点到根节点的一系列哈希值）有效地证明一条数据属于树的叶子节点。

什么是 Trie？

Trie（检索树的缩写，也称为前缀树）是一种类似树的数据结构，用于高效地存储和检索键值对，尤其是在键是字符串或序列时。

trie 的每个级别表示键中的一个字符，从根到叶的路径对应于整个键。键之间的共享前缀仅存储一次，这使得 trie 对于具有公共前缀的数据集非常节省空间。

让我们看一个玩具示例，以便更容易理解。假设我们要存储以下键值对：

我们的玩具 trie 看起来像这样：

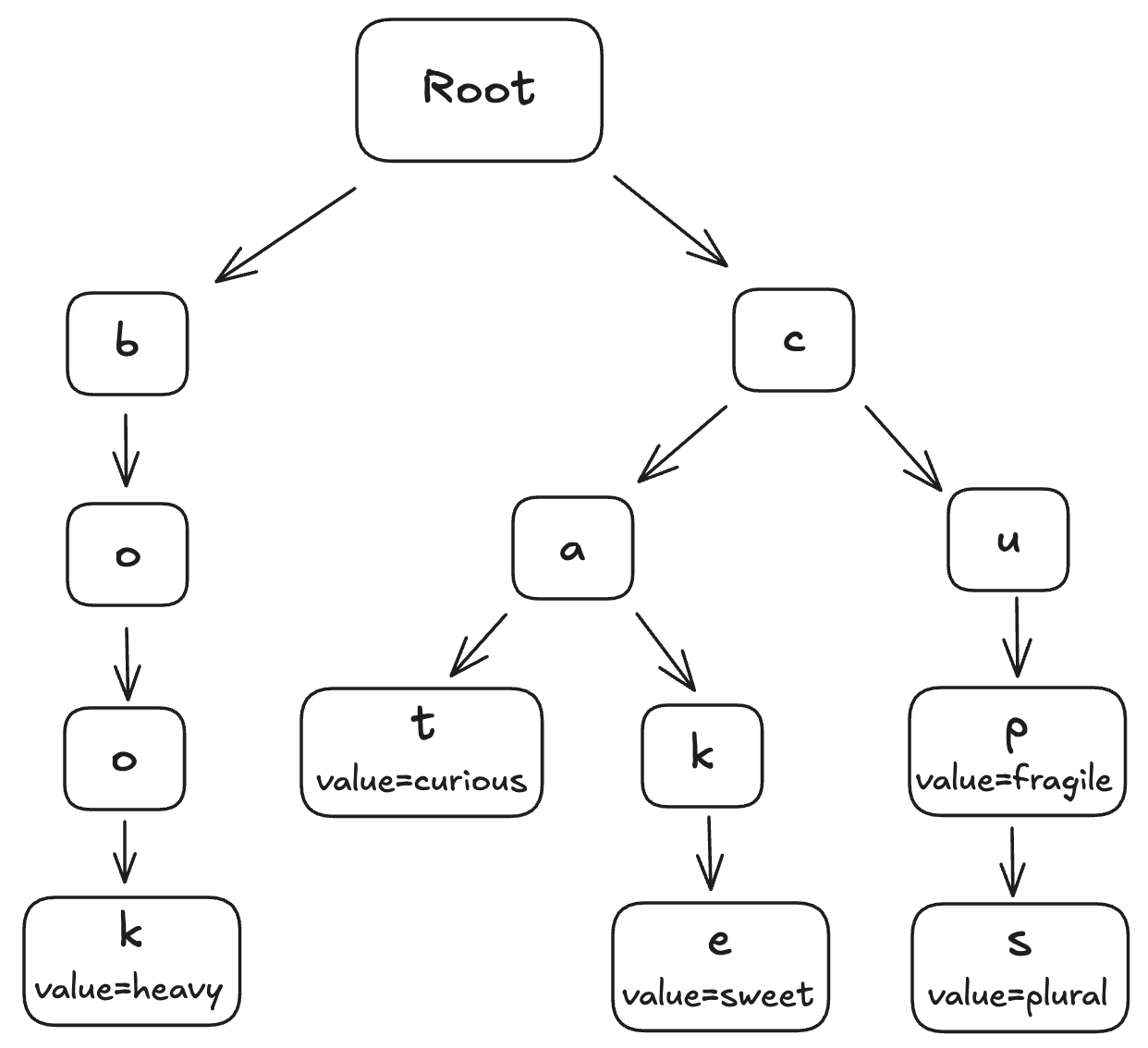
要查找键 "cake" 的值：

1. 从根开始。
2. 按照与键的字符对应的节点：c -> a -> k -> e。
3. 在最后一个节点 e 检索值 "sweet"。

什么是 Merkle Patricia Trie？

以太坊使用一种专门的 trie 形式，称为 Modified Merkle Patricia Trie (MPT)。该名称结合了三个核心思想：

• Trie: 用于按共享前缀组织键。
• Merkle: 每个节点都被哈希，形成一个 Merkle 结构，可以对整个数据集进行密码学验证。
• Patricia: Practical Algorithm to Retrieve Information Coded in Alphanumeric 的缩写——trie 的一种变体，可压缩节点具有单个子节点的路径（也称为 radix 或 compact trie）。

MPT 在以太坊中如何使用？

以太坊使用多个 MPT，但我们将仅关注其中一个，即 State Trie，并将其用作解释它们如何工作的示例。

在 State Trie 中，每个帐户的状态都存储为一个键值对，其中：

• 键 是帐户地址的 Keccak-256 哈希值。
• 值 是帐户，它是四项数组的 RLP 编码：[nonce, balance, storageRoot, codeHash]。

为了达成共识，当出现一个包含交易集的新区块时，每个以太坊节点都需要执行所有这些交易并验证所有节点的结果状态是否相同。但是，比较每个帐户的计算成本非常高，因此它们使用 MPT 代替。以太坊所有帐户的状态都存储在一个名为 State Trie 的 Merkle trie 中，该 trie 在每次交易执行后都会不断更新。为了达成共识，节点只需比较 StateRoot（State Trie 的根）。如果两个节点具有相同的 StateRoot，则它们的状态匹配。

不可变性：MPT 的巨大优势

以太坊需要能够轻松地恢复到以前的状态：当节点对下一个区块存在分歧时，需要进行区块链分叉。这是可能的，因为 trie 保留了旧状态，而不是直接删除或修改它。trie 是持久的和可版本化的，而不是可变的就地结构。

当状态发生变化时（例如，帐户余额更新），trie 会为已更改的路径创建新节点，而 trie 的其余部分（未更改的部分）会被重用。因此，可以通过它们的根访问以前的 trie 版本。每个区块都在其标头中存储一个状态根，并且该根唯一地标识了当时整个以太坊的状态。因此，如果以太坊需要回滚，它只需使用先前区块的状态根即可。由于旧节点从未被删除，因此 trie 可以有效地重建旧状态。这意味着以太坊只需切换回较早的根哈希即可恢复旧状态。

MPT 结构

让我们解释一下 State Trie 是如何构建的。正如我们上面所说，这个 trie 的键由地址的哈希值组成，表示为十六进制字符串。正如我们在玩具示例中展示的那样，trie 的每个节点将存储十六进制字符串的一个字符，也就是单个 nibble （四位数据）。

MPT 中有三种类型的节点：

1. 分支节点（Branch Node）

   • 它存储一个 17 项数组。
   • 前 16 项表示键前缀可以是的每个十六进制数字之一。如果键前缀是数字 ii，那么在索引 ii 处，你将找到指向继续键路径的下一个节点的指针。
   • 最后一项可以在键在此处结束的情况下分配一个值。

   • 例子：

     [0x, 0x, child_hash, 0x, 0x, other_child_hash, 0x, 0x, 0x, 0x, 0x, 0x, 0x, 0x, 0x, 0x, value]

     在这里，"0x" 表示未使用的槽，即没有子节点的数字。

2. 扩展节点（Extension Node）
   • 它是压缩共享键前缀的优化结果。
   • 它存储一个包含共享键前缀和指向下一个节点的指针的两项数组。
   • 例子：[shared_prefix, child_hash]
3. 叶子节点（Leaf Node）
   • 它存储一个包含剩余键片段及其关联值的两项数组，结束路径。
   • 例子：[key_remaining, value]

这三种类型的节点都存储一个以 RLP 编码的单个数组。指向某个节点的指针始终是存储该 RLP 字符串数据的哈希值。根可以是任何类型，但通常，由于我们有很多数据，因此根是一个分支节点。

节点和奇偶校验标志

当逐个 nibble（或逐个字符）遍历键路径时，我们最终可能会得到一个需要存储奇数个 nibble 的叶子节点或扩展节点。但是由于所有数据都存储在字节中，这会产生一个问题。例如，如果我们想存储 nibble 1，我们将不得不将其保存为 01，但我们将无法判断它来自两个 nibble 01，还是来自单个 nibble 1。为了指示我们是存储偶数个还是奇数个 nibble —— 以及我们正在处理的节点类型（叶子或扩展）——部分路径以以下标志作为前缀。

示例：逐步构建 MPT

理解 MPT 的最佳方法是查看完整的示例。让我们模拟一个真实的 State Trie。假设我们有五个帐户的数据，这些帐户转换为以下键值对：

正如我们前面提到的，键应该是帐户地址的哈希值。由于以太坊使用 Keccak-256，因此键应该是 32 字节长（或 64 个十六进制字符）。但是，对于此示例，我们将使用短得多的键，以便生成的 trie 不会太大且更易于理解。以太坊还使用优化，例如内联小节点，为了清楚起见，我们将在本示例中跳过这些优化。

现在我们准备好构建 MPT：

1. 从一个空的 MPT 开始，并添加第一个键值对：(0x616b6c64, 0x01)。因为它只是一个键，所以它会生成一个只有一个叶子节点的 trie。要创建该节点，请按以下方式进行：

   • 写入一个两项数组： 第一个元素应该是整个键，第二个元素应该是值。将前缀标志 20 添加到第一个元素，指示该节点是一个叶子节点，并且该键具有偶数个 nibble。然后，该数组应如下所示：["0x20616b6c64","0x01"]。
   • 在 RLP 中编码数组： 你可以使用 RLP 转换器 或此 python 脚本：

import rlp

key = bytes.fromhex("20616b6c64")
value = bytes.fromhex("01")
encoded = rlp.encode([key, value])
print(encoded.hex())

这应该输出这个十六进制：c78520616b6c6401。

• 使用 Keccak-256 哈希 RLP 编码 以获取此节点的指针。你可以使用 在线哈希器 或此脚本：

from eth_utils import keccak

rlp_bytes = bytes.fromhex("c78520616b6c6401")
hash_pointer = keccak(rlp_bytes)
print(hash_pointer.hex())

这应该输出：

4e2d0fbe6726eac15c5ecf49a4e1f947aa50e0531f4f3e98b8e1577ba52e1783

生成的 MPT 应如下所示：

2. 添加第二个键值对：(0x616b6c65, 0x02)。由于此键与前一个键共享前 7 位数字，因此我们按以下方式进行操作：

   • 为每个键构建一个叶子节点： 在每个叶子节点中，数组的第一个元素应该是剩余路径，但由于两个键共享除最后一个数字之外的每个数字，因此剩余路径为空。因此，我们应该只在那里写入标志 20，指示我们位于叶子节点中，并且该路径具有偶数个数字（零个数字）。之后，像我们在步骤 1 中所做的那样，在 RLP 中编码数组并哈希 RLP 编码。
   • 构建一个分支节点： 创建一个 17 项数组。在索引 44 处写入第一个键的叶子节点的哈希值，并在索引 55 处写入第二个键的叶子节点的哈希值。在 RLP 中编码该数组并哈希该编码。

   • 构建扩展节点和根节点： 创建一个包含共享前缀作为第一个元素和先前构建的分支节点的哈希值作为第二个元素的两项数组。由于共享前缀具有奇数个数字，因此将标志 1 添加到其中。在 RLP 中编码该数组并哈希该编码。

     

3. 添加键值对 (0x616b6c78, 0x03)：

   • 添加一个叶子节点： 注意，在这种情况下，由于新键与前一个键共享除最后两位数字之外的所有数字，因此数组的第一个项目将只有一位数字作为剩余路径，并且标志 3 指示它是一个具有奇数个路径数字的叶子节点。
   • 添加一个分支节点： 它的数组应包含在索引 66 处，步骤 2 中构建的分支节点的哈希指针，以及在索引 77 处，我们最近添加的新叶子节点的哈希指针。
   • 添加一个扩展节点： 根将是另一个扩展节点。它的数组应包含共享前缀作为第一个元素，以及最近添加的分支节点的哈希值作为第二个元素。由于共享前缀具有偶数个数字，因此将标志 00 添加到其中。

当前的 trie 应如下所示：

4. 继续以这种方式添加最后两个键值对，遵循与先前键相同的步骤。完成后，你应该具有以下 MPT：

Trie 证明

现在让我们了解 MPT 中的证明是什么样的。继续前面的示例，假设我们要证明键值对 (0x616b6d31, 0x04) 属于我们的 State Trie。我们如何构建证明？

该证明将包含 StateRoot 0x13ea...bed7（根节点的哈希值）以及从根开始并向下遍历 trie 的路径，沿着目标键的每个数字，直到到达其叶子节点。让我们逐步了解如何构建此路径：

1. 路径的第一个元素是根节点的 RLP：0xf851...8080。

   如果我们解码此 RLP，我们发现根是一个分支节点。它表示的数组除了索引 3 和 6 之外，都具有所有空槽（因为所有键都以数字 3 或 6 开头）。这意味着根节点分支为两个子节点。由于我们要查找的键的第一位数字是 6，因此我们需要查看存储在数组中索引 6 处的哈希值，然后移动到该节点。

2. 我们移动到下一个节点，并将它的 RLP 内容存储为路径的第二个元素：0xe583...67e9。

   此节点是一个扩展节点，因为所有以 6 开头的键都共享相同的后四位数字：16b6。为了确定接下来要去哪里，我们解码 RLP 并得到一个两项数组。第二个项目为我们提供了我们需要访问的下一个节点的哈希值。

3. 同样，我们移动到下一个节点，并将它的 RLP 内容存储为路径的第三个元素：0xf851...8080。

   此节点是一个分支节点。由于我们的键继续使用数字 d，因此我们需要查看存储在此节点数组中索引 dd 处的哈希值，然后移动到此哈希指向的节点。

4. 最后，我们到达叶子节点：0xc482203104。我们存储此最终节点的 RLP 内容，这样，证明就完成了。

然后键值 (0x616b6d31, 0x04) 的证明应如下所示：

state_root = 0x13ea549e268b5aa80e9752c6be0770cffba34d2b1aa1f858cb90f3f13ac3bed7

proof_path =
    [\
    0xf851808080a0a26b2ac124718443aeed68fa0309225d0c8dd9dbee45685909e92fb594e1a4638080a02ccd118c9470c051689543b233ab109ad74d2fb4f57eb429c4d43294d6ae686780808080808080808080,\
    0xe5831616b6a0917fa5cab26d915e2a89a263a578fa5f9ecf02cc0b1d3eeb433e7f32499267e9,\
    0xf851808080808080808080808080a0cc97f12ea3217345e666974cd81b117ca02404f19c15d31158ac1d1e55398706a0822a55ca308aa885ad385d5e61aabaca54c2e4361eb03b6f851668c0f095ab77808080,\
    0xc482203104\
    ]

验证

如果验证者收到某个键的 StateRoot 和证明路径，他如何验证该证明是否有效？

与标准 Merkle 树的一个关键区别是验证方向。虽然典型的 Merkle 证明是从下往上验证的（从叶子节点到根节点），但 Merkle Patricia Tries 证明是从上往下验证的。该过程从 StateRoot 开始，并使用提供的路径逐个节点地向下遍历 trie，最终到达目标叶子节点。

假设验证者收到上述键值 (0x616b6d31, 0x04) 的证明。然后，他必须按照以下步骤操作：

1. 哈希 路径的第一个元素，并检查它是否与给定的 StateRoot 匹配。的确：

keccak(bytes.fromhex(
    "f851808080a0a26b2ac124718443aeed68fa0309225d0c8dd9dbee45685909e92fb594e1a4638080a02ccd118c9470c051689543b233ab109ad74d2fb4f57eb429c4d43294d6ae686780808080808080808080"
)).hex() ==
    "13ea549e268b5aa80e9752c6be0770cffba34d2b1aa1f858cb90f3f13ac3bed7"

2. 解码 路径的 第一个 RLP 元素，并验证索引 66 是否具有第二个路径元素的哈希值。的确：

rlp.decode(bytes.fromhex(
    "f851808080a0a26b2ac124718443aeed68fa0309225d0c8dd9dbee45685909e92fb594e1a4638080a02ccd118c9470c051689543b233ab109ad74d2fb4f57eb429c4d43294d6ae686780808080808080808080"
))[6].hex() ==
    "2ccd118c9470c051689543b233ab109ad74d2fb4f57eb429c4d43294d6ae6867"

3. 解码 路径的第二个 RLP 元素。你会发现一个两项数组，其第一个元素是 0x1616b6。由于它的第一位数字是 1，我们知道我们位于扩展节点上。检查其余数字是否与我们要查找的键相对应。验证该数组的第二个元素是否是路径的下一个元素的哈希值。

4. 解码 第三个路径元素。你将找到一个分支节点。验证索引 dd 处是否存储了路径元素的哈希值。

5. 解码 路径的最后一个元素。你会发现一个两项数组，其第一个元素是 0x2031。由于它的前两位数字是 20，我们知道我们到达了一个叶子节点。验证第一个项目是否包含剩余键的数字 31，第二个项目是否包含键的值 0x04。

总结

Merkle Patricia Trie 是以太坊状态管理的支柱。它结合了 tries 的键导航效率和 Merkle 树的密码学保证。这种结构允许以太坊高效且安全地存储、验证和恢复状态。借助 MPT，以太坊节点可以独立执行交易，并通过简单地比较状态根来验证共识，从而实现可扩展且无需信任的区块链系统。在即将发布的文章中，我们将阐述如何对 MPT 更新进行算术化，并展示我们如何验证包含证明。

• 原文链接： blog.lambdaclass.com/an-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～