嵌入式费用市场与ERC-4337(第一部分)- 经济学
- 以太坊中文
- 发布于 2024-05-14 18:55
- 阅读 744
本文探讨了嵌入式费用市场问题,即在其他费用市场中“存在”的费用市场。以以太坊的ERC-4337协议为例,分析了用户通过捆绑者访问链时产生的费用机制,并建立了一个简单的模型来量化捆绑者的成本函数。此外,还讨论了捆绑者如何通过签名聚合来优化成本并提高效率,以及用户在不完全信息下可能面临的博弈论问题,为后续研究用户体验和市场结构奠定基础。
作者:Davide Rezzoli ( @DavideRezzoli) 和 Barnabé Monnot ( @barnabe)
非常感谢 Yoav Weiss ( @yoavw) 向我们介绍这个问题,Dror Tirosh ( @drortirosh) 对草案的有用评论,以及 4337 团队的支持。评论 ≠ 背书,所有错误均为作者的责任。
这项工作是为 ROP-7 做的。
交易费用机制已成为理解区块生产者在希望交易的用户和用户进行交易的“链”(或“协议”)之间的中介作用的主力模型。鉴于能够使用链提供的一些供应,区块生产者必须仲裁哪些用户将有能力使用链上执行这种稀缺资源,以及以什么代价。在以太坊上,对于成本问题,区块生产者受到 EIP-1559 费用机制的约束,该机制动态地逐块设置一个保留价格,称为“基础费用”。基础费用是一个价格,以每单位 gas 表示,用户交易必须支付才能被包含和执行。用户可以提供超出基础费用的所谓“优先费用”,以进一步激励拥塞时的区块生产者。
在本笔记中,我们研究了嵌入式费用市场的问题,即“存在”于其他费用市场中的费用市场。Maryam Bahrani、Pranav Garimidi 和 Tim Roughgarden 在最近的一篇论文“ 后 MEV 世界中的交易费用机制设计”中在不同的背景下讨论了这个问题。在本文中,作者模拟了搜索者的使用,进一步中介了用户和区块生产者之间的链访问。搜索者的费用市场由最大化一个称为 MEV(或最大可提取价值)的数量的目标驱动。
在我们的设置中,用户希望访问链,但不使用协议可识别的交易来表达他们的需求。相反,用户产生“操作”,由称为“捆绑者 (bundler)”的实体捆绑,然后捆绑者发起一个协议可识别的交易,将这些操作打包在一起以进行执行。因此,对于 EIP-1559 费用机制,捆绑者是链的用户,但实际用户必须首先获得捆绑者捆绑包的包含资格,然后才能获得链的包含资格。换句话说,我们可以将此设置视为 区块共同创建这一更大问题的一部分,该问题随着(部分)构建者/搜索者以及包含列表而出现。
我们希望这些动态尽可能透明,这样与直接上链相比,用户就不会有过多的认知负担或被捆绑者不正当利用的机会。我们甚至希望获得更强大的结果,即在摊销成本允许用户享受更大福利的情况下,用户确实可以从捆绑者的中介中受益。
为了研究直接费用市场及其嵌入式(子)机制之间的区别,我们必须精确地说明捆绑者遵守的经济约束。在以下部分中,我们提供了一个简单的捆绑者成本函数模型,该模型受到实践的驱动,特别是参与 ERC-4337 协议的捆绑者,我们简要回顾一下该协议。
模型
ERC-4337 中的捆绑
希望通过捆绑者在链上执行某些活动的用户会发出一个用户操作(UserOp,或操作)。此 UserOp 从用户的钱包发出,例如,在与 DApp 交互后。一旦 UserOp 被广播,一些接收到该操作的捆绑者可能会决定将其包含在一个捆绑包中。捆绑包是一个“外部账户”(EOA)元交易,它将其 bundle.calldata 字段中包含的 UserOp 的数据写入其中。捆绑者发出捆绑包,以便由区块生产者包含在区块中(我们将在未来的说明中讨论捆绑者和区块生产者之间的关系)。
一旦捆绑包包含在区块中,并且该区块进入链中,则该捆绑包将与区块中的其他交易一起执行。本质上,捆绑包执行步骤如下:
- 预验证: 捆绑者的 EOA 交易将消耗 21,000 gas,并且对 EntryPoint 合同的调用将设置关键变量,以跟踪操作循环中操作的执行情况。
-
操作循环: 对于捆绑包中包含的每个操作,都会执行以下两个步骤:
- 验证步骤: UserOp 执行包含验证步骤的操作,该验证步骤编码在用户最初部署的“智能合约钱包”中(在初始 UserOp 期间)。验证步骤可以简单地检查签名,或者执行更复杂的操作来“授予” UserOp 继续执行的权利。验证步骤由
op.verificationGasLimit计量。 - 执行步骤: UserOp 的核心,执行步骤执行
op.callData中描述的操作。此步骤也经过计量,使用op.callGasLimit。
- 验证步骤: UserOp 执行包含验证步骤的操作,该验证步骤编码在用户最初部署的“智能合约钱包”中(在初始 UserOp 期间)。验证步骤可以简单地检查签名,或者执行更复杂的操作来“授予” UserOp 继续执行的权利。验证步骤由
正如之前的分解所明确说明的那样,预验证步骤执行一次,从而可以摊销所有包含用户的预验证成本。当捆绑包执行时,所有成本(例如,block.basefee + 捆绑者支付给包含它们到区块生产者的优先费用)都由捆绑者承担,捆绑者必须确保用户操作能够充分补偿其产生的成本。我们在以下部分中对这些陈述进行了精确的说明。
捆绑包的费用市场模型
我们尝试与经典的费用市场模型保持一致。希望发出操作的用户 t 对于操作的执行具有一定的价值 v_t。我们假设所有操作都具有相同的大小 S(即,验证和执行步骤使用相同的 gas),因此我们将所有数量表示为每单位 gas 的价格。
用户通过在操作中发出出价 b_t 来表达他们被包含的意愿。目前,我们不假设用户表达其包含出价的具体语法,例如,像使用 EIP-1559 那样,能够表达最大费用和优先费用以及他们的操作。用户操作收集在 M mempool 中,表示这些操作在包含之前的待处理状态。
EIP-1559 费用市场公开了一个称为“基础费用”的保留价格 r,捆绑者在执行其捆绑包时必须承担该费用。如果捆绑包包含 n 个操作,则捆绑者必须至少花费 n \times S \times r。此外,由于捆绑包消耗“预验证 gas”,例如,某个数量 F,则捆绑者还将支付 F \times r。捆绑包中包含的操作由集合 B 给出。
捆绑者成本函数
我们现在考虑捆绑者因将其捆绑包包含在区块中而产生的成本。
链上成本函数: 当基础费用为 r 时,发出捆绑包B的捆绑者会产生以下成本:
C_\text{on-chain}(\mathbf{B}, r) = F \times r + n \times S \times r
捆绑者问题反映了 [Roughgarden 2021] 中表达的区块生产者问题 。在那里,区块生产者必须确保提供一些值 \mu 来补偿其将额外交易添加到其区块的成本(例如,\mu 可以补偿区块的额外负载,这会延迟其传播,从而增加重组风险)。然后,区块级别的费用市场必须确保区块生产者至少获得总成本 n \times S \times \mu 的补偿,如果区块生产者在其区块中包含 n 个交易。捆绑者级别的费用市场将要求至少补偿捆绑者因其嵌入的较大费用市场而产生的外生成本 C_\text{on-chain}(\mathbf{B}, r)。
ERC-4337 提供了摊销成本的可能性,而不仅仅是分担预验证 gas 成本。如果所有操作都为其验证步骤采用相同的签名方案,则这些操作的签名可能会被捆绑者聚合,这样,与其在链上验证 n 个签名,不如验证单个签名。在这种情况下,捆绑者成本函数将需要考虑捆绑者在执行聚合时产生的链下成本。在下文中,我们假设此类成本与操作数量成线性关系,与 [Wang et al., 2024] 中的假设类似,边际成本为 \omega。
我们还考虑了由于聚合节省而减少的每个操作的 gas 消耗。聚合后,操作不需要发布其签名,但它们确实需要额外的配对操作。在 calldata 成本很高但配对操作/计算很便宜的链上,聚合因此提供了每个操作的节省。在这种情况下,我们将交易的减少大小表示为 S' < S。我们还需要考虑增加的预验证 gas 使用量 F' > F,现在其中包含单个链上聚合签名的发布和验证。
聚合成本函数: 当基础费用为 r 时,使用聚合签名发出捆绑包B的捆绑者会产生以下成本:
C_\text{agg}(\mathbf{B}, r) = F' \times r + n \times S' \times r + n \times \omega
在本说明中,我们将不再赘述,但是人们还可以考虑捆绑者在将其捆绑包结算到 rollup 时可能需要花费的数据发布成本。我们提出了两种对此进行建模的方法,并将此问题留给以后的工作:
- 捆绑者本人负责数据发布(例如,作为排序器),因此需要从用户那里获得必要的资金,以支付最终的数据发布成本。
- 或者,捆绑包级别的费用市场嵌入到更大的批处理级别的费用市场中,通过该市场,rollup 向 rollup 用户(包括捆绑者)公开由于拥塞而需要支付的金额(例如,基础费用)和最终的数据发布成本。在这种情况下,rollup 负责平衡其自身的未来成本与当前的收入。
重新审视费用市场数量
我们现在可以正式表达捆绑包级别的费用市场的相关概念,从以前的文献中直接推导出来,同时考虑到嵌入。
捆绑包级别的分配规则: (捆绑包级别)分配 x 根据当前 mempool M 和基础费用 r,决定捆绑者在其捆绑包中包含的一组用户操作。
x_t(\textbf{M}, r) \in \{0, 1\}, \forall t
捆绑包级别的支付规则: 给定选定的操作集B,支付规则为每个包含的用户分配费用:
p_t(\textbf{B})
用户效用函数: u_t(b_t) = v_t - p_t(\mathbf{B})
原则上,我们可以允许存在燃烧规则 q_t(\mathbf{B}),该规则表示捆绑者可能不会收到所有包含用户付款的总额。但是,我们在此说明中未考虑它。
(近视的)捆绑者效用函数: u(\mathbf{B}, r) = \sum_{t \in \mathbf{B}} p_t(\mathbf{B}) - C(\mathbf{B}, r)
如果对于每个 mempool M和基础费用 r,近视的捆绑者通过遵循分配规则 x 的建议来最大化其效用(即,设置 B = x(\textbf{M}, r)),则捆绑包级别的 TFM (x, p) 对近视的捆绑者 (MBIC) 具有激励相容性。
形成多个捆绑包
在上一节中,我们仅考虑了捆绑者发出单个捆绑包的可能性。但是,我们可能对捆绑者从 mempool 中可用的操作中生成多个捆绑包的可能性感兴趣。给定 mempool M,令 P(\mathbf{M}) 表示 mempool 的分区集,将每个操作分配给单个捆绑包(我们可以假设对于每个分区,都有一个索引为 0 的集合,其中包含所有未分配给捆绑包以进行包含的操作)。然后,分配规则返回操作分配到的分区中的集合的索引。
x(\textbf{M}, r) \in P(\textbf{M})
我们可以将分区 x(\textbf{M}, \beta) 输出的捆绑包集合写为 \mathcal{B}(x(\textbf{M}, r))。直观上,这些捆绑包由不属于索引为 0 的集合的操作组成。给定一组捆绑包 \mathcal{B},则支付规则为:
p_t(\mathcal{B})
用户效用函数变为:
u_t(b_t) = v_t - p_t(\mathcal{B})
并且捆绑者效用函数变为:
u(\mathcal{B}, r) = \sum_{B \in \mathcal{B}} \sum_{t \in {B}} p_t(\mathcal{B}) - C(\mathcal{B}, r)
捆绑者博弈
将交易包含在区块中必须给区块生产者带来一定的收益 \mu,例如,在 [Roughgarden, 2021] 中,假设收益与交易规模成线性关系。此数量表示区块生产者向其区块添加额外交易的机会成本,例如,增加其 gossip 延迟,从而增加其区块被重组的机会。在 Proof-of-Stake 中,即使协议的计划允许足够的时间来传播完整区块,定时博弈也引起了“最后一秒”的传播动态,这再次使此 \mu 参数变得相关。
无论如何,我们可以观察到区块级别的成本分摊问题和捆绑包级别的成本分摊问题非常不同。在区块级别,交易无需知道区块内发生的其他事情就可以根据 EIP-1559 设计其包含出价(它可能想知道关于 MEV 发生的事情 [Bahrani et al., 2024],但我们现在将此视为一个单独的问题)。在捆绑包级别,捆绑包开销成本不再与交易数量成线性关系,但固定开销可以由许多交易摊销。此外,如果用户操作的聚合成本与交易数量成非线性关系(例如,某些证明实际上在正在证明的大小上是次线性的),则可以跨许多用户摊销总成本。
这导致了以下博弈:捆绑者希望用户像为最坏情况 出价一样出价,在这种情况下,用户在捆绑包中是孤立的,并且必须自己补偿全部开销 gas F。实际上,用户将面临在其操作中设置三个相关参数的问题:
- 可以根据用户在 EIP-1559 下使用的启发式方法来设置
op.maxPriorityFeePerGas和op.maxFeePerGas,也就是说,给定对其希望 operation 消耗的 gas 的一些估计量,用户将设置这些属性以校准他们愿意在最坏情况下支付多少 (maxFee),以及他们愿意充值多少以支付最终区块生产者 (maxPriority)。但是用户应该如何估计 gas? op.preVerificationGas是 UserOperation 的一个属性,必须将其设置为指示用户的 operation 计划消耗的“额外 gas”量。在我们的模型中,我们令 F 表示此“固定 gas 开销”。如果捆绑包中包含 n 个用户,则每个用户应设置preVerificationGas = F / n。但是,如果用户准备 operation 时考虑的是最坏情况,他们将设置preVerificationGas = F。
然后,preVerificationGas 是用户通过其进行调解出价并尝试考虑捆绑者摊销成本的主要向量。假设 n 个用户确实带着他们的 operation 进入市场,并且所有人都被捆绑者说服以最坏的情况出价,即他们独自在一个捆绑包中。我们还将假设为了本示例的目的,用户将其 maxPriorityFeePerGas 设置为零。然后,这 n 个用户都设置了 preVerificationGas = F,并且捆绑者能够输出一个捆绑包来补偿他们:
n \times F \times r
而他们必须承担以下成本:
F \times r
一旦他们发布了将所有 n 个操作捆绑在一起的捆绑包。这使捆绑者获得了利润 \pi = (n-1) \times F \times r。
这种情况可以用一个两阶段博弈表示,在这个博弈中,用户首先生成他们的用户操作,然后捆绑者决定捆绑它们。我们假设用户不拥有关于当前待处理用户数量的信息,因此无法估计捆绑者摊销其固定成本的真实能力。
在第一阶段,用户发送他们的操作,这些操作提交给他们的属性,例如 preVerificationGas。在第二阶段,接收到所有用户交易的捆绑者决定输出一个捆绑包或一组捆绑包。有趣的是,即使用户知道有多少其他用户将在第一阶段参与,也就是说,即使 n 是所有用户的常识,捆绑者也可能通过威胁玩 \mathcal{B}_\text{pessimistic} = \{ \{ 1 \}, \{ 2 \}, \{ 3 \}, \dots, \{ n \} \} 来迫使设置最坏情况 preVerificationGas = F,即威胁将每个用户保留在他们自己单独的捆绑包中,并向他们收取最大数量的 gas F。
请注意,此威胁可能不可信,因为用户会期望捆绑者更喜欢玩 \mathcal{B}_\text{ideal} = \{ \{1, 2, 3, \dots, n \} \},即输出一个包含所有操作的捆绑包,实现 \pi。但是,用户可能无法访问 n 的真实值,因此他们无法以迫使捆绑者理想地捆绑所有用户的方式设置其 preVerificationGas。
[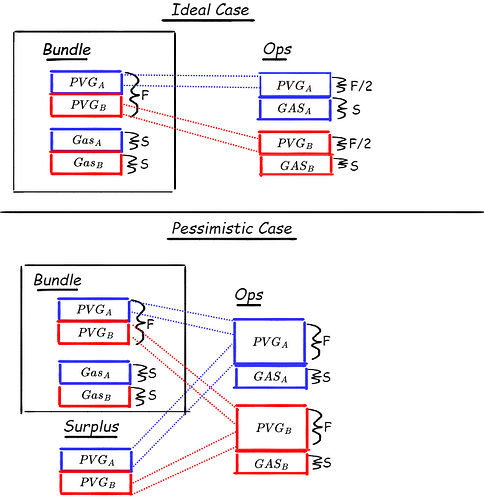\\
理想情况:成本在捆绑包中的用户之间分摊。悲观情况:用户过度支付,成本未分摊。731×755 77.6 KB](https://ethresear.ch/uploads/default/original/3X/2/a/2a1e3be0f917af5d2d8d3fa4c487a848543c76b2.png "理想情况:成本在捆绑包中的用户之间分摊。悲观情况:用户过度支付,成本未分摊。")此模型的扩展可以考虑贝叶斯情况,在这种情况下,用户可以访问 n 的分布,也就是说,他们可能预期某些随机变量 n 个用户会在任何给定的时间步出现,根据某些分布(例如,泊松到达),即使他们事先不知道随机变量的结果。这可能会导致效率低下的结果,如下例所示:
Alice 期望除了她自己之外还有 9 个其他用户出现,因此她将其
preVerificationGas设置为 1,因为她知道 F = 10。Alice 的 value 和所有其他用户的 value 与他们设置preVerificationGas = 3兼容,但她尝试为包含支付尽可能少的费用。事实证明,市场上只出现了 5 个用户,他们也将他们的preVerificationGas设置为 1。捆绑者将不会获得F = 10单位 gas 的补偿,因此捆绑者不会输出捆绑包,用户获得的效用为 0。这显然不是最佳的,因为例如,用户可以将preVerificationGas设置为 2 并获得 1 的效用(他们愿意设置的最大preVerificationGas减去他们为包含支付的实际preVerificationGas)。
未来的工作
正如捆绑者博弈所表明的那样,分配问题面临着希望被捆绑者包含的用户。在下一份说明中,我们将解决不同的方法来恢复用户的“良好 UX”,以防止他们过度支付给对捆绑包容量 Demand 了解更多的捆绑者。下一次探索将需要了解将用户、捆绑者和构建者/区块生产者联系在一起的市场结构。
- 原文链接: ethresear.ch/t/embedded-...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Gas 优化概述 2117 浏览
- 后量子签名聚合:一种折叠方法 - 密码学 572 浏览
- EIP-5564 隐私地址:最有希望快速普及到用户的隐私技术 967 浏览
- ERC-4337 Paymaster:更好的用户体验,隐藏的风险 846 浏览
- 让以太坊所有的 Layer2 再次感觉像一条链 3385 浏览
- EIP-1559:动态费用交易(类型 0x02)详解 860 浏览

