发现一种gas优化的新方法

发现

最近看到一个很有意思的项目FORT，说他有意思，一个是其产品的逻辑新颖，折现计算机和无限流动性，这些看起来很技术化的概念有意思。另外一个是其合约的写法有很多有意思的地方。在其中就看到了一种通过对数据进行编码的gas优化方法，下面对这种方法做一个简单的分析。

问题

我们知道，以太坊上gas消耗最大的跟存储相关的指令，因此针对存储进行优化是一个重要的方向。而在做项目的时候，一些数据，像价格，余额等，通常都用uint256来表示，这是一个以太坊存储槽的大小，也就是说，一个价格就需要单独占用一个存储槽。因为不同的代币，精度和价格相差极大，导致我们不能简单的用更小的数据类型来表示价格，而这个问题，在FORT的代码里面有一种很简单高效的解决方法，下面是从其github上的代码：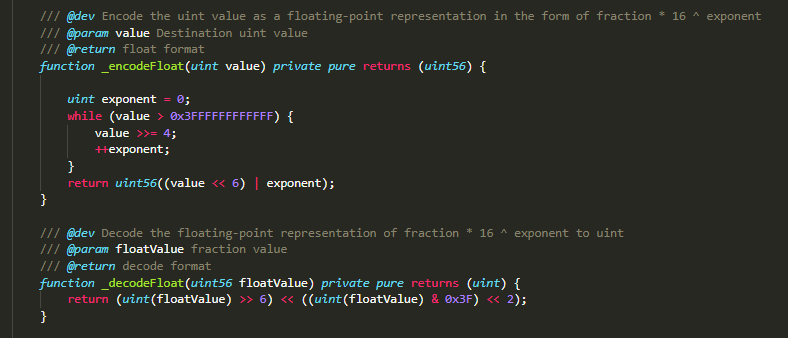

如上图所示，其通过_encodeFloat()方法将uint256编码成一个uint56，通过_decodeFloat()两个方法，将编码的uint56解码成uint。从而让原本需要占用256位的数据压缩到了56位，这个压缩比还是很高的。那么，这是什么原理呢？

分析

1. _encodeFloat()方法是将原来的uint256表示成一种类似科学计数法的形式，这类似计算机中的浮点表示形式，形式如 fraction * 16 ^ exponent。编码时循环对目标数据除以16，直到其值在 fraction 可表示的范围内，此处是50位二进制，因此其值范围是 0 ~ 0x3FFFFFFFFFFFF。而指数用6位存储，底数是16。计算发现，这种表示方法能够表示的数据范围可以覆盖uint256能够表示的范围。
2. _decodeFloat()则是按照这种浮点表示法还原原始值，只要确保输入是经过_encodeFloat()得到的，就可以保证还原得到的值符合要求。

效率

1. 效率也会影响gas消耗，在_encodeFloat()编码时循环对目标数据除以16，直到其值在 fraction 可表示的范围内，根据原始值大小的不同，需要循环的次数也不尽相同，绝大部分值只要少量或者不需要循环就可以完成编码，最大循环次数不会超过51次。
2. _decodeFloat()的实现则更高效，只需要进行4次位运算就可以完成还原。

精度

这种方法采用50位存储fraction，这决定了数据的精度，经过计算可知，这可以达到15位10进制有效数字的精度，这是一个极高的精度，用于表示价格这样的数据，在通常情况下是完全足够的。

应用

这种表示方法能够表示超大的数据范围，同时提供极高的精度，具体精度可以通过调整fraction占用的位数来按需调整。这是一种通用方法，当目标数据符合此特征时，可以采用此方法表示，从而大大节省存储空间，优化gas消耗。

结语

FORT合约代码里面有很多类似的技巧，可以看出，开发者在节省gas上是煞费苦心，其中很多技巧是通用解决方案，我准备后续继续写一系列的文章来解读这些技巧，另外，为了更好的理解合约，我也会研究合约的结构并记录下来。