前面我们已经大致了解了 uniswap 的交易算法, 今天我们一起看看 Uniswap手续费是怎么计算的

可能很多读者认为手续费计算并不重要, 因为手续费对于用户而言就是扣掉千分之三的 input而已, 没什么难度. 但是我在阅读 pair的 mintFee函数时, 一开始有些看不懂, 琢磨了两三天才把它的逻辑搞明白, 所以今天就跟大家分享一下心得体会, 实际上平台的协议手续费收取算法是比较有意思的内容, 我们通过对手续费计算过程的学习, 可以窥探系统设计者背后的设计思路, 以及代码实现中用到的 gas 优化技巧

手续费的产生

假设 swap前两个代币数量为 A1, B2, swap后为 A2, B2

前面已经有介绍, 在不收手续费的情况下, swap前后满足 A * B = K 不变.

但是在收取手续费的情况下, 实际的有效输入是 effectiveInput = amountIn 0.997, 这部分有效输入 effectiveInput 进行 swap 交易后满足交易后的 A2' B2' = A1 * B1

但是实际的输入量是 effectiveInput 1000 / 997, 这样池子里真实的 A2 B2 将会大于原有的 A * B, 池子的财富增加了 在 LP 代币总量不变的情况下, 每个 LP 持有人分享到的财富就会增加, 这个增量就是手续费

下面是 core/UniswapV2Pair.sol 中的 swap的代码片段:

  function swap(uint amount0Out, uint amount1Out, address to, bytes calldata data) external lock {
      ...
      { // scope for reserve{0,1}Adjusted, avoids stack too deep errors
          uint balance0Adjusted = balance0.mul(1000).sub(amount0In.mul(3));
          uint balance1Adjusted = balance1.mul(1000).sub(amount1In.mul(3));
          require(balance0Adjusted.mul(balance1Adjusted) >= uint(_reserve0).mul(_reserve1).mul(1000**2), 'UniswapV2: K');
      }
      ...
  }

上面的代码中, 池子要求 扣掉 3/1000 的输入后, 仍然满足 A2'B2' >= A1B1 而真实的 A2, B2 中至少有一个满足 A2 = A2' + input 3/1000 或者 B2 = B2' + input 3/1000, 因此 A2B2 > A1B2, 池子的总财富得到增加

做市商(LP)的手续费

下面的讨论中, 用 lp 表示部分 pair 代币, lp_supply 表示 pair 代币总量 做市商的手续费不需要计算, 在池子财富增加的情况下, lp代币总量不变, 那么每个做市商持有的lp将会分到更多的 tokenA 和 tokenB, 在 removeLiquidity时, 根据 lp/lp_supply 这个比值获得更多的 tokenA 和 tokenB

平台收取的协议手续费

平台收取的手续费占手续费产生的财富增量的 1/6, 如果开启协议手续费, 那么做市商收取 2.5/1000, 平台收取 0.5/1000

平台手续费是通过定向增发 lp 给项目方的 feeTo账户实现的

那么问题来了, 这个增发量应该是多少呢?

相信很多同学在看 _mintFee这个函数的时候, 和我开始拿到代码一样没有看明白,

所以这是我们今天介绍的重点.

首先我们假设最简单的情况: 在一系列swap后, 池子的财富 tokenA 和 tokenB 是等比例增加的, 例如: A 和 B 都增加了 12%, 那么很简单, feeTo账户将会得到两个代币增量的 1/6 , 即总量的 2/112, 因此发行的 lp = lp_supply * 2/110, 这样增发之后 , 平台方持有的lp/新的lp_supply 刚好等于 2/112

但是如果 A 和 B 不是等比例增加, 应该发多少 lp 给项目方呢? 例如 A 增加了 10%, B 增加了 20%, 那么应该分配多少的 tokenA 和 tokenB 给项目方? 15%, 还是 12%, or 18% ??? 注意lp增发的分配方式下, 项目方得到 tokenA 和 tokenB的数量, 相对于库存 A, B 应该是相同的比例, 不可能 得到 10%/6 的 tokenA, 20% /6 的 tokenB, 只能是 x% 的 tokenA 和 tokenB

那么这个 x% 应该是多少?

也就是说, 当池子中 A 和 B不是等比例增加的时候, 应该认为池子的财富增加了多少 ? 假设在状态1, 池子中的代币余额为 A1, B1, 此时规定池子的财富是 w1 经过一系列交换后, 到达状态2, 此时代币余额为 A2, B2, (假设 A2/A1 != B2/B1, 两个代币不是等比例增加) 那么我们认为池子的财富 w2 是多少?

这个问题对于手续费计算很重要, 因为只有定义了池子中财富度量的标准, 我们才能计算出财富增加的比例, 从而 mint 正确的 lp 代币 作为协议手续费

交易池的财富度量: rootK

下面的讨论中, 我们用 A, B 表示交易池的两个代币数量, w 表示交易池的财富值

现在我们需要制定一个度量标准 f, 并规定交易池的财富值 w = f(A,B)

只有制定了这样的度量标准, 我们才能计算出任意时刻交易池的财富值 w, 进而计算出需要 mint 给项目方的 lp : lp = lp_supply (w2 - w1) (1/6) / w1

可能阅读过 Uniswap源代码的同学可能已经知道了, f 的定义方法, 就是取两个代币数量的几何平均值 sqrt(A*B) 这个值我们将他命名为 rootK

但是为什么是 rootK? 为什么是几何平均值, 而不是代数平均值 (A+B)/2, 或者为什么不直接取 A*B ?

接下来我们将会证明, 为什么rootK 可以作为, 而且必须是rootK(或者rootK * 常系数)作为交易池的财富度量.

首先我们规定两条公理:

1. 如果A, B是等比例增加, 那么财富值也按照相同的比例增加: 即 w2/w1 = A2/A1 , 同时 w2/w1 = B2/B1 这一点很好理解, 只有成比例增加, 才能确保 lp 持有人分到的财富是公平的, 否则先撤销流动性和后撤销流动性得到的代币不相等.

2. 假设两个状态下, AB 的值相同, 认为财富值相同, 即: 若 A1 B1 = A2 * B2, 那么 w2 = w1 这是 Uniswap 交易算法决定的, 假设每一笔交易都是公平交易, 兑换者和交易池都不吃亏, 兑换前后交易池的财富不变.

   下面是推导过程:

   问题: 假设交易池在初始状态 A1, B1 的时候, 规定财富是 w1, 经过一系列 swap 交易后, 交易池的代币数量为 A2, B2, 且 A2/A1 != B2/B1 求此状态下财富值 w2 = ?

   证明: 现在我们邀请一名交易者来做swap, 让他用 A2/A1 和 B2/B1 中比值较小的币种, 换取比值较大的币种, 确保交易之后的 A3, B3 刚好满足 A3/A1 = B3/B1, 这笔交易不收手续费

   根据前面的第二条假设前提 , 状态2到状态3财富不变. w3 = w2

   同时又可以根据第一条等比例原则, 得出等式: w3 / w1 = A3 / A1

   但是由于不知道 A3 的值, 还不能直接算出 w3 不过由于 A3/A1 = B3/B1, 所以可以得到 w3/w1 = sqrt[ (A3B3) / (A1B1) ]

   将 w3 换成 w2, A3B3 换成 A2B2, 就可以计算出了 w2 的值: w2/w1 = sqrt(A2B2) / sqrt(A1B2)

   可以看到, 财富值 w 的度量要满足前面两个前提条件, 只能是 sqrt(A*B)的常数倍, 为了简化, 这个常数就取为1.

   因此, Uniswap定义的交易池财富值度量值 w = sqrt(A*B), 这个值在代码里的变量名为 rootK

   kLast变量 和协议手续费的算法

   平台的协议手续费, 在每次 addLiquidity和 removeLiquidity之前征收.

   UniswapV2Pair.sol 使用一个变量 kLast 用来记录最近一次征收协议手续费之后的K值, 它是 rootK 的平方, 即AB: uint public kLast; // reserve0 reserve1, as of immediately after the most recent liquidity event

   每次征收手续费时, 会计算当前的 K, 如果大于上一次的 K, 即 kLast, 那么就会征收手续费, 征收数量为: (1/6) (当前rootK - 上一次的 rootK) , 即 (1/6) ( sqrt(reserve0 * reserve1) - sqrt(kLast) )

   下面是 UniswapV2Pair.sol 中的 _mintFee方法:

   // if fee is on, mint liquidity equivalent to 1/6th of the growth in sqrt(k)
   function _mintFee(uint112 _reserve0, uint112 _reserve1) private returns (bool feeOn) {
     address feeTo = IUniswapV2Factory(factory).feeTo();
     feeOn = feeTo != address(0);
     uint _kLast = kLast; // gas savings
     if (feeOn) {
         if (_kLast != 0) {
             uint rootK = Math.sqrt(uint(_reserve0).mul(_reserve1));
             uint rootKLast = Math.sqrt(_kLast);
             if (rootK > rootKLast) {
                 uint numerator = totalSupply.mul(rootK.sub(rootKLast));
                 uint denominator = rootK.mul(5).add(rootKLast);
                 uint liquidity = numerator / denominator;
                 if (liquidity > 0) _mint(feeTo, liquidity);
             }
         }
     } else if (_kLast != 0) {
         kLast = 0;
     }
   }

   可能很多朋友有疑问, 上面的代码中, mint的数量 为什么是 (rootK - rootKLast)/(5倍rootK + 1倍rootKLast) 而不是 (rootK - rootKLast)/6倍rootKLast 呢? 别急, 我们通过下图, 看看要增发多少 lp, 使得lp分到的财富刚好是增量的 1/6: 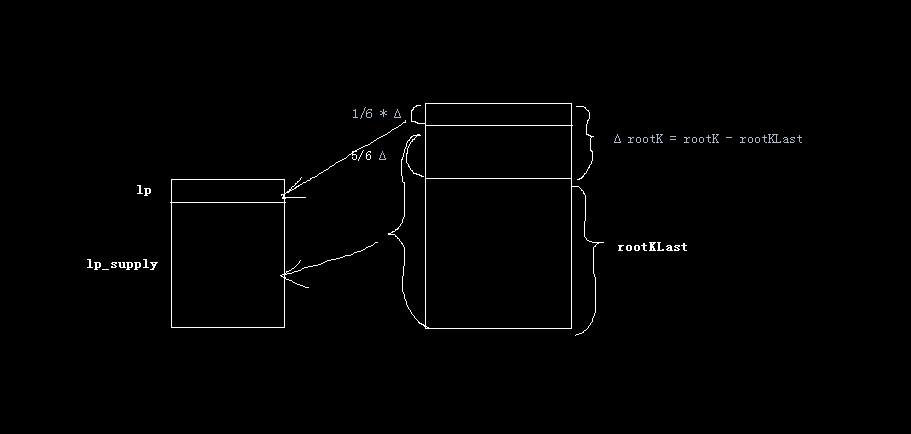如上图所示, 为了得到新增财富的 1/6, 需要增发的 lp 应该满足: lp/lp_supply = (∆/6) / [(∆5/6) + rootKLast ], 这里 ∆ = rootK - rootKLast 解出 lp = lp_supply ∆ / (5*rootK + rootKLast), 与源代码的计算方法一致, 证实了 Uniswap 收取的协议手续费就是总手续费的1/6.

   手续费的记录和结算:

   为了记录手续费, UniswapV2Pair 使用了一个变量 kLast, 用来记录最后一次结算后的 K值 (reserve0 * reserve1)

   我们记录手续费真正需要的是 rootK - rootKLast 但是为什么记录的是 kLast 而不是 rootKLast呢? 为了节省gas,

   只有当程序检查到 当前 K > kLast 时 , 才会执行开方运算, 计算出 rootK - rootKLast 如果当前 K 和之前的 kLast 一致, 那就没必要开方.

   所以记录手续费虽然真正关注的是 rootK 的差值, 但是保存的变量是 kLast.

   需要注意的一点是, K值不仅包含了手续费产生的财富增量, 他还会受到 addLiquidity 和 removeLiquidity 的影响, 如果上次记录 kLast后,发生了添加/撤销流动性事件, 那么交易池的财富增量包含了添加流动性的增量,手续费产生的增量, 同时还会受到撤销流动性的抵消, 这样就无法正确的追踪 "因手续费而产生的财富增量了", 那要怎么解决呢.

   办法就是在任何添加/撤销流动性之前把迄今为止的手续费结清, 在流动性操作结束后重新开始记录 K 值, 这样我们每次结算时 rootK - rootKLat 就不存在加减流动性产生的变化了, 全部都是手续费产生的增量.

   因此, 可以看到在 Pair合约的 mint() 和 burn()中, 每次添加/撤销流动性之前, 都会调用 _mintFee() 结算协议手续费, 而在函数的最后都有一条语句重新记录 kLast:

   // this low-level function should be called from a contract which performs important safety checks
   function mint(address to) external lock returns (uint liquidity) {
     ...
     /****************************************************************************
      *  流动性操作之前, 结清迄今为止产生的手续费
      ****************************************************************************/
     bool feeOn = _mintFee(_reserve0, _reserve1);
   
     ...
     //按照输入的 balance-reserve, mint 代币给 to(即项目方钱包)
     ...
   
     _update(balance0, balance1, _reserve0, _reserve1);
   
     /****************************************************************************
      *  流动性操作结束后, 重新记录 kLast, 使得rootK - rootKLast 始终不受增减流动性的影响
      ****************************************************************************/
     if (feeOn) kLast = uint(reserve0).mul(reserve1); // reserve0 and reserve1 are up-to-date
     emit Mint(msg.sender, amount0, amount1);
   }

   那么为什么不使用更直观的方式记录手续费呢? 比如下面我们用一个变量记录 "迄今为止未结算手续费"

   uint256 public cumulatedFee;
   
   function swap(xxx, xxx, xxx ...){
   
     uint256 rootKBefore = sqrt(reserve0 * reserve1);
   
     ...
     //执行swap交易
     ...
   
     _update(balance0, balance1, _reserve0, _reserve1);
   
     cumulatedFee += ( sqrt(reserve0 * reserve1) - rootKBefore );
   
   }

   虽然上面的代码可以更直观的方式实现手续费结算, 但是, 每次swap需要读取和存储一次 cumulatedFee, 计算两次开平方, 通常 swap 执行的次数要远大于添加/撤销流动性的次数, 从gas经济性考虑, 使用前面的 kLast 方法更好.

好的, 今天我们一起分析了 Uniswap的手续费计算方法和代码实现细节, 相信大家应该对 Uniswap的手续费算法有了更加深入的理解, 我们下期再见!