多项式承诺,正在重塑整个区块链
- w3hitchhiker
- 发布于 2023-01-30 13:20
- 阅读 5636
多项式承诺正在重塑整个区块链的架构,不论是在链的数据结构优化上,模块化区块链的数据可用性上,还是零知识证明系统上都将大有作为。
作者:Xiang|W3.Hitchhiker 修订:Evelyn|W3.Hitchhiker
不同多项式承诺方案列表
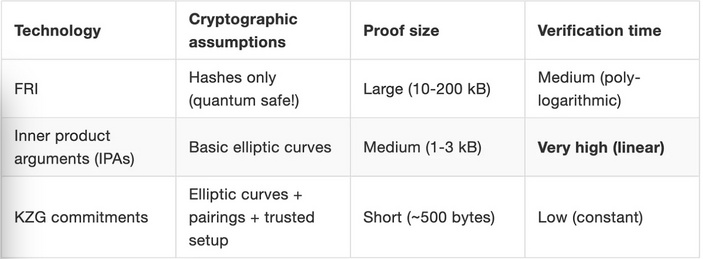
上表中,FRI 是 Starkware 采用的多项式承诺方案,可以实现量子级别的安全,但证明的数据量却是最大;IPA 是 Bulletproof 和 Halo2 零知识算法默认的多项式承诺方案,验证时间相对较长,采用的项目有门罗币,zcash 等,前两者是不需要初始可信设置的。
由上图可以看出在证明大小与验证时间上,KZG 多项式承诺的优势比较大,KZG 承诺也是目前应用最广的一种多项式承诺方式。但 KZG 是基于椭圆曲线,配对函数,需要初始可信设置的。
ETH 升级路线与多项式承诺的关联
在 ETH 相关生态及其未来升级路线中,都可以看到多项式承诺的踪影。
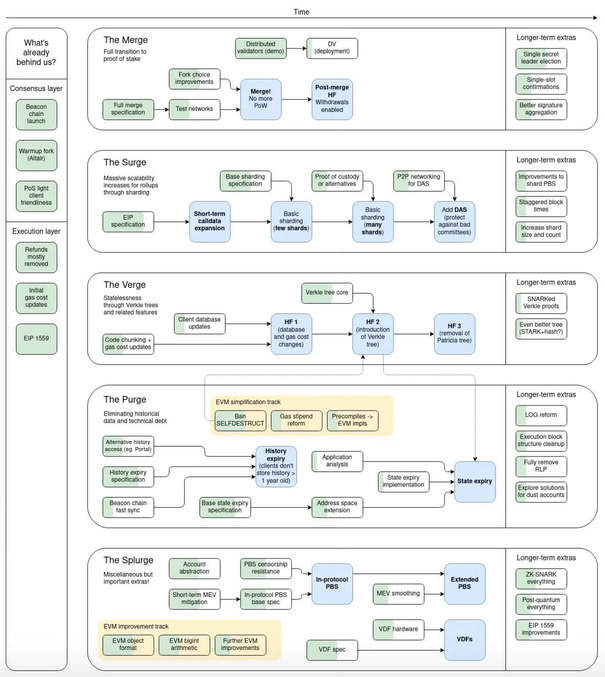
The Merge:
现时的以太坊主链和 Beacon Chain 将会合并,原本的 PoW (工作量证明) 共识将会转变成 PoS (权益证明)。
The Surge:
添加DAS(数据可抽样性功能),极大的提高ETH的扩展性,通过 Danksharding 增强 rollup 性能。
The Verge:
引入 Verkle 树 (Verkle Trees) 的设计来优化以太坊上的数据存储。
The Purge:
通过剔除历史数据和消除技术债务,验证者不再需要使用大量硬盘空间去进行验证工作。
The Splurge:
四个不同部分升级后的协调,旨在减少错误 (Bugs) 的出现和确保网络能畅顺运作,还有就是 EVM 改进和添加账号抽象模型等。
其中 The Surge 升级将借鉴多项式承诺技术实现数据可抽样性功能,The Verge 升级将利用多项式承诺来优化其数据结构,ETH L2 的 zkrollup 也都采用了多项式承诺来实现其零知识证明带来的性能拓展。
什么是 KZG 多项式承诺
此文这里只介绍较好理解的 KZG 多项式承诺,KZG 多项式承诺(KZG Polynomial Commitment)也被称为卡特多项式承诺方案,是 Kate,Zaverucha 和 Goldberg 一起发表的。在一个多项式方案中,证明者计算一个多项式的承诺,并可以在多项式的任意一点进行打开,该承诺方案能证明多项式在特定位置的值与指定的值一致。
之所以被称为承诺,是因为当一个承诺值(椭圆曲线上的一个点)发送给某对象(验证者)时,证明者不可以改变当前计算的多项式。他们只能够对一个多项式提供有效的证明;当试图作弊时,它们要不无法提供证明,要不证明被验证者拒绝。
KZG 数学原理
详细可参考 Qi Zhou 博士在 Dapp Learning 讲解的关于 KZG 视频。
在理解 KZG 之前,可以先了解一下多项式、群、环、域、椭圆曲线、生成元、配对公式、朗格朗日插值等数学定义。
多项式可以表达为一下结构: $f(x)=a_0+a_1x+a2x^2+...+a{n-1}x^{n-1}+a_nx^n$ 这里是一个椭圆曲线群: $\mathbb G_1=[0,G_1,G_1+G_1=[2]G_1,[3]G_1,[q]G_1]where[q+1]G_1=0$ 椭圆曲线群特征:
- $[n]G_1=[n]_1$可以非常快的计算出来
- $[n]X=Y$,给出 $X$ 和 $Y$ ,是非常难找到 $n$ 的(理算对数算法)
当多项式与椭圆曲线群$\mathbb G_1$相结合,可得: $[f(x)]G1=[\sum^n{i=0}a_ix^i]G1=\sum^n{i=0}a_i=\sum^n_{i=0}[a_i][x^i]_1$
具有可信设置的多项式承诺
通过多方计算可信设置(Trust Setup)生成无人知晓的$s,s \in \mathbb F_q $
- 没有人知道s(可理解为无人知晓的私钥)
- $[s^i]G_1=[s^i]_1,i=1,...$这部分是公开的,每个人都知道(公开的公钥)
此时,我们可以计算承诺: $C=[f(s)]1 = \sum^n{i=0}[s_i][s^i]_1$ 此时要找到另外一个多项式$g(x)$,让$g(s)=f(s)$几乎是不可能的。 s的值并未有人知晓,但$[s^i]G_1$是可以公开的,所以 C,我们是可以计算出来的,卡特承诺为 C,C是椭圆曲线群上的某一点。
单个证明
卡特证明单个数据的公式推衍如下,由于椭圆曲线群只支持加法同态,无法支持多项式之间的乘法,这是就需要通过配对函数解决,
其中配对函数用到的$G_2$,是另外一个椭圆曲线群,其中$[s^i]G_2$ 在setup的时候也已经计算并准备好。
给出$x_i,x_y$,想要证明$f(x_i)=y_i$, $f(x)-y_i=g(x)=(x-x_i)q(x)$
$[f(s)-y_i]G_1=[(s-x_i)q(s)]G_1$
$f(s)G_1$就是卡特承诺,所以可得: $C-[y_i]_1=[(s-x_i)q(s)]G_1$
由于椭圆曲线群并不支持运算多项式之间的乘法运算,所以此时得采用配对函数去解决 $e:\mathbb G_1 × \mathbb G2 \to \mathbb G{\mathbb T}$
$e(C-[y_i]G_1,G_2) = e([q(s)]_1,[(s-x_i)]_2)$
其中$[q(s)]_1$就是卡特承诺的证明,也是椭圆曲线群的一个点,其他的数据是公开或者一开始 setup 就已经计算并准备好的,这里的 $y_i$ 可以理解为要保存的数据。
批量证明
更进一步,我们来看看怎么使用一个群元素,计算证明一个多项式在任意多个点的取值,还是利用插值多项式,有一个包含k个点的列表$(x_0,y_0),(x_1,y1),...(x{k-1},y_{k-1})$。通过插值公式可以找到一个次数小于k的多项式来经过这些点。得到该多项式的公式$I(x)$,现在我们假设$f(x)$经过了所有的点,那对于多项式$f(x)-I(x)$而言,在$x_0,x1,...,x{k-1}$处而言,都是零值。
可得零多项式: $z(x)=(x-x_0)(x-x_1)...*(x-x_{k-1})$
$q(x)=(f(x)-I(x))/z(x)$
注意:因为f(x)-I(x)能被z(x)所有的线性因子整除,所以它能被z(x)本身整除。
$[f(s)-I(s)]G_1=[q(s)z(s)]G_1$
计算$(x_0,y_0),(x_1,y1),...(x{k-1},y_{k-1})$的卡特证明:$[q(s)]_1$
最后证明等式相等
$e([q(s)]_1,[z(s)]_2)=e(C-[I(x)]_1,G_2)$
仅仅提供一个群元素,你就能证明任何数量的计算,甚至是百万个!
由于z(s),q(s)都有与$G_1$相乘,z(s)与$G_2$相乘,所以setup,Powers of Tau for KZG proofs 在以太坊上要把对应参数都计算下来并公开,选择z(s)与$G_2$相乘是因为尽量减少计算。
具体应用场景
多项式承诺应用方向总结起来可以分为 3 大类:
-
数据可用性(ETH Surge 升级,ETH danksharding,降低 L2 成本,模块化数据可用性项目 Avails)
-
数据结构优化(MPT 树改为 Verkle 树,ETH Verge 升级,无状态客户端,实现 ETH 的轻量的验证节点)
-
零知识证明系统(Zksync,Zkswap,Scroll,PSE 给 Zk 提供多项式承诺方案,大大提升链的拓展能力)
1. 数据可用性
DAS(数据可用性抽样)
核心目的:数据缺失则无法通过大多数节点抽查
尽力做到:占用带宽小,抽样过程所需计算量小
纠删码(celestia)
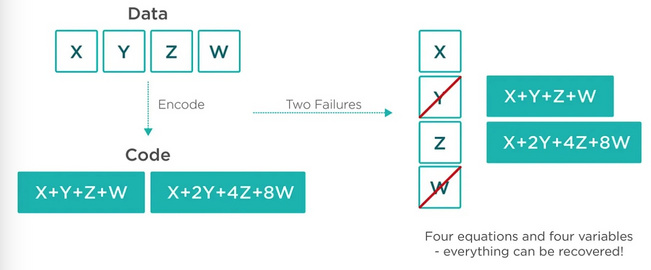
纠删码会增加额外数据块,这种情况很容易通过抽样调查发现,从而提升安全性。
以上图为例,有 4 个数据,一次只能抽样一个,假设一个数据有问题,每个用户抽样发现错误的概率是 1/4,但是加入两数据块后,还是一个数据有问题,用户抽样发现的概率可以高达 1/2(3/6)。这样就能大幅提升安全性。
KZG 也可实现纠删码,利用拉格朗日公式:
比如把 (0,3),(1,6) 带入公式可得,y=3x+3
y1,y2 可以理解为要保存的数据,
对应点(2,8)(3,12) 等等,其中 y 值可以作为纠删码数据,其中任意两个点都可以推出原多项式公式系数。
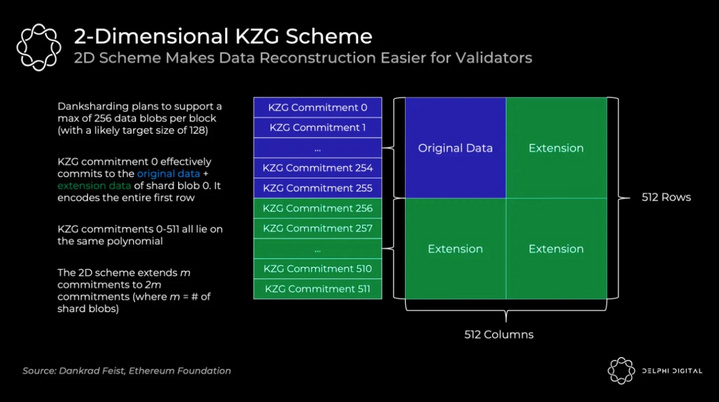
不同数据可用性项目组成
Celestia = Tendermint (cosmos) + 2d 纠删码 + 欺诈证明 + Namespace merkle tree + IPFS 基础设施(数据存储用的 IPFS Blockstore,传输网络用的 IPFS 的 Libp2p 与 bitswap,数据模型用的 IPFS 的 Ipld)
Polygon Avail = Substrate(Polkadot) + 2d 纠删码 + KZG 多项式承诺 + IPFS 基础设施
ETHprotoDankSharding = Blobs 数据(数据可用性的存储,替换现有的 calldata)+ 2d 纠删码 + KZG 多项式承诺(未定,方案目前仍在讨论)+ ETH 基础设施
EIP-4844 升级将在 The Merge 之后的下一个以太坊分叉升级中引入“proto-danksharding”并添加blob交易类型(EIP-4844),这有望将第 2 层 Rollup 的可扩展性提高,同时为实现完全分片(sharding)铺平道路。
Blob Transaction
-
增加一种新的交易类型,这种交易包含额外的存储空间 —— Blobs
-
Blob 开始只有 128 KiB 的存储空间
(1)一个交易最多包含 2 个 Blob,即 256 KiB
(2)一个 Block 最多包含 16 个,即 2 MiB;Target 是 8 个,即 1 MiB(可扩大)
-
Blob 以 KZG Commitment Hash 作为 Hash,用于数据验证,作用和 Merkle 类似
-
节点同步链上的 Blob Transaction 后,Blob 部分会在一段时间后过期删除
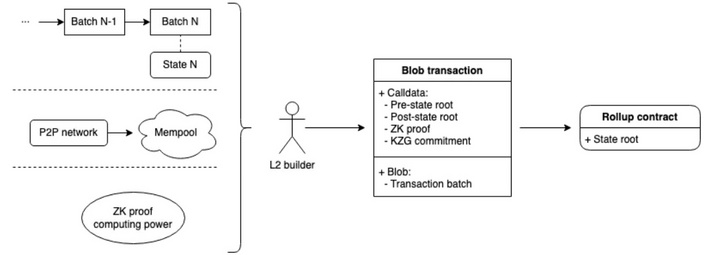
L2 需要通过更新目前在 L1 的合约,以支持 DankSharding。
Celestia 通过欺诈证明实现。当见证人发现数据没有被正确采用删码技术,那么这个人就会将欺诈证明提交从而来提醒其他节点。但是这里需要最少诚实假设(至少连接到一个诚实节点)和同步假设(当有人给我发送欺诈证明的时候,需要确保我能在一定时间内收到通知)。
protoDanksharding 后的以太坊和 Polygon Avail 则采用了 KZG 多项式承诺(KZG commitments) 的方法。
KZG 多项式承诺方案,理论上要优于欺诈证明方案,带宽需求更小,抽样所需计算量也更小,也免去了欺诈证明中的包括少数诚实假设和同步假设等的安全假设。 未来 ETH 也有意引入抗后量子密码学(参考 stark,采用哈希,不在使用椭圆曲线作为基础),避免量子计算机攻击。
2. 数据结构优化 Verkle Tree
Verkle Tree 的概念在 2018 年推出,作为 ETH 升级的一个重要部分,其相比于 Merkle Tree,在 Proof 的大小上,有着很大的提升;对于规模在十亿级别的数据,Merkle Tree 的 proof 大约需要 1kB,而对于 Verkle Tree, 它将小于 150Bytes。
与 Merkle Tree 一样 Verkle Tree 也能实现 Proof of Inclusion(PoI),而且只需 KZG root 和 Data 就能验证,不需要额外的 Proof,更省带宽。
-
需求:Stateless Client
(1)节点不存完整的 State Tree,只获取需要的 State 来验证 Block
(3)对 State Tree 的 PoI 有更高的性能要求
-
回顾 Data Availability 里的 KZG commitment
-
每个 leaf 都是 polynomial 上的点
-
constant size proof,和 leaf 数量无关
-

3. Verkle Tree
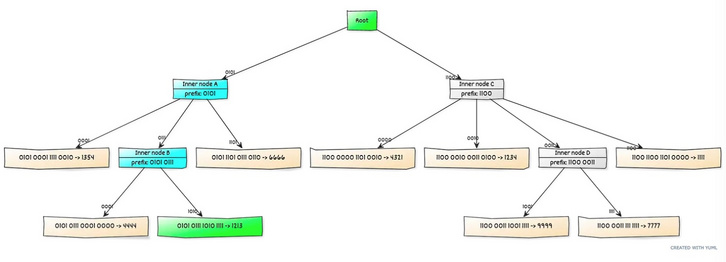
空间复杂度从 Merkle Patricia Tree 的 $O(16 \cdot log{16}N)$ 、Merkle Tree 的 $O(logN)$,提升为 $O(log{16}N)$
在不同树结构中构建证明,更新证明,以及证明所需的复杂度:
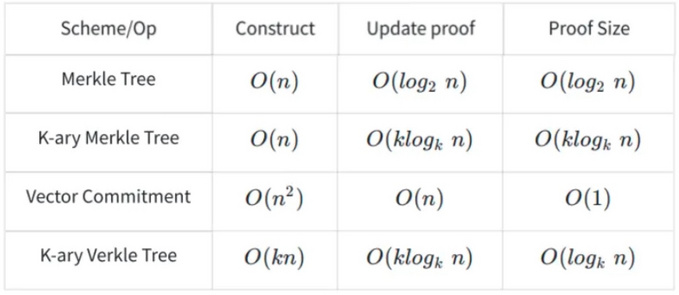
比特币采用的 Merkle Tree ,以太坊目前采用的是Merkle Patricia Tree(K-ary Merkle Tree)。假设 ETH 直接采用 Vector commitment 的方案对原始数据进行存在性证明,其可以获得O(1)复杂度的证明,但是构建证明的复杂度和更新证明的复杂度分别为 $O(n^2),O(n)$。因此,为了在它们之间保持一个平衡,未来以太坊的 Verkle Tree 里采用的 K-ary 的 Verkle Tree 的方案,k为16。
Verkle 方案不需要以太坊客户端下载完整的状态数据,使得 ETH 验证者轻节点成为可能(甚至可支持手机运行),多项式承诺(Verkle 树的多项式承诺方案,早期考虑的 KZG,近期还是考虑用 IPA)需要的证明空间复杂度大幅降低,带宽量需求量也大幅减少。
3. 零知识证明系统
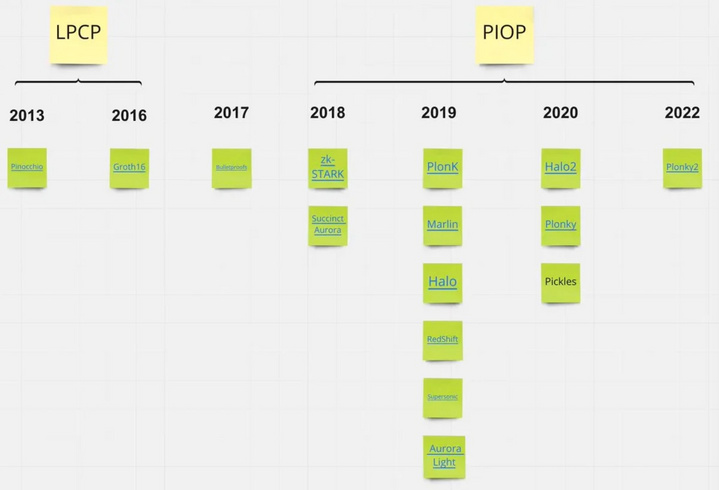
早期 zk 技术(Groth16)属于线性 PCP 类。 除要求可信设置外,主要缺点是如果需要为不同的计算(不同的电路/多项式)提供证明,都需要一次新的设置。近期 zk 技术 PIOP 类支持通用初始设置和透明设置(不需要信任假设)。
新的 zk 证明系统通常可以描述为 PIOP(Polynomial Interactive Oracle Proof,多项式交互预言证明)+ PCS(Polynomial Commitment Scheme,多项式承诺方案)。前者可被视为是证明者用来说服验证者的约定程序,而后者使用数学方法确保该程序不会遭到破坏。项目方可以按需修改 PIOP,且可以在不同 PCS 中进行选择。
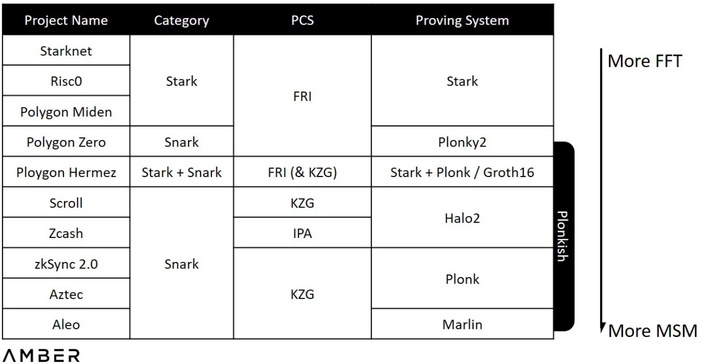
由 Amber 文章里的图可以看到 zk 系公链项目采用 KZG 方案的最多,有 Ploygon Hermez,Scoll,Zksync2.0,Aztec,Aleo,Manta,以太坊基金会支持的 PSE(隐私与扩展探索团队)也采用的 KZG 方案。而 Starknet,Risc0,Polygon Miden 采用的是 FRI 方案,Ploygon Zkvm(Hermez) 则是 FRI 与 KZG 的结合。
值得一提是,一些新的零知识证明系统支持多项式承诺方案的切换,KZG 未来也可以切换成其他多项式承诺方案。
总的来说,多项式承诺正在重塑整个区块链的架构,不论是在链的数据结构优化上,模块化区块链的数据可用性上,还是零知识证明系统上都将大有作为。其他地方是否还存在应用场景也是非常值得探索与跟进的。
本文首发于:https://w3hitchhiker.mirror.xyz/iY0IB8yc9arir9yAEE-SmjgKdT7HP2CKsJOU5nS1Nc4
- ZK编年史:哈希登场 315 浏览
- GKR 教程 - 加速零知识证明的密码学方案 - Vitalik 1489 浏览
- Aleo 2025 年路线图及 Varuna 深入探索 1898 浏览
- 我们对Jagged多项式承诺的Succinct解释 1506 浏览
- EIP-4844 准备情况检查清单 1674 浏览
- 密码学 - 斯巴达 1852 浏览
- KZG变体:第一部分,单变量 - ZKSECURITY 1354 浏览
- 向量承诺(VCs) 2877 浏览
- KZG与常见的SNARK零知识算法特点分析 2172 浏览
- zkVM Jolt:更新 3028 浏览
- 零知识乘法 2305 浏览
- PCS: Binius explained - Chen Yanlong 1438 浏览

