stark证明实操python实现02
- w3hitchhiker
- 更新于 2023-03-29 16:41
- 阅读 1031
通过stark简单证明实操python-02
接上篇回顾：https://learnblockchain.cn/article/5453 译者：Xiang｜W3.Hitchhiker
第二部分：约束
在这一部分中，我们将在轨迹a 上创建一组约束。 当且仅当轨迹表示 FibonacciSq 的有效计算时，约束将是轨迹单元格中的多项式（而不是有理函数）表达式。
我们将分三步实现：
-
首先指定我们关心的约束（FibonacciSq 约束）。
-
将 FibonacciSq 约束转换为多项式约束。
-
将它们转换为表示多项式的有理函数当且仅当原始约束成立时。
步骤 1 - FibonacciSq 约束
其计算结果恰好超过 G1，其中 G 是由 g 生成的“小”组。
步骤 2 - 多项式约束
开始动手
首先，由于这是与第 1 部分不同的笔记，让我们运行以下代码，使此处的所有变量都具有正确的值。请注意，它最多可能需要 30 秒，因为它会重新运行多项式插值。
from channel import Channel
from field import FieldElement
from merkle import MerkleTree
from polynomial import interpolate\_poly, X, prod
from tutorial\_sessions import part1
a, g, G, h, H, eval\_domain, f, f\_eval, f\_merkle, channel = part1()
print('Success!')
你将获得三个约束中的每一个作为两个多项式的商，确保余数是零的多项式。
步骤3 - 有理函数 (实际的多项式)
第一个约束 The First Constraint：
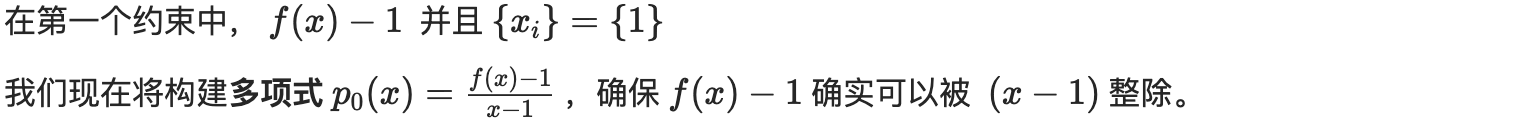
numer0 = f - 1
denom0 = X - 1
事实上 f(x)-1 有一个根为 1 在意味着它可被 (x-1) 整除。运行以下代码块以说服自己 numer0 模 denom0 的余数为 0，因此除法确实会产生一个多项式：
numer0 % denom0
运行以下代码块以通过将 numer0 除以 denom0 来构造 p0，即表示第一个约束的多项式。
p0 = numer0 / denom0
跑测试：
assert p0(2718) == 2509888982
print('Success!')
第二个约束：
numer1 = f - 2338775057
denom1 = X - g\*\*1022
p1 = numer1 / denom1
跑测试：
assert p1(5772) == 232961446
print('Success!')
第三个约束：
lst = \[(X - g\*\*i) for i in range(1024)\]
prod(lst)
有关更多信息，请参阅博客文章 Arithmetization II。
让我们暂停一下，看一个关于多项式如何组成的简单例子。之后我们将生成第三个约束。
组合多项式 (a detour)
q = 2\*X \*\* 2 + 1
r = X - 3
把 q r 组合产生一个新的多项式：
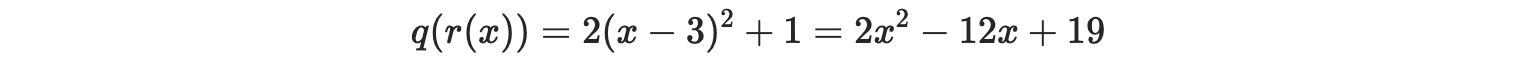
返回到多项式约束
numer2 = f(g\*\*2 \* X) - f(g \* X)\*\*2 - f\*\*2
print("Numerator at g^1020 is", numer2(g\*\*1020))
print("Numerator at g^1021 is", numer2(g\*\*1021))
denom2 = (X\*\*1024 - 1) / ((X - g\*\*1021) \* (X - g\*\*1022) \* (X - g\*\*1023))
p2 = numer2 / denom2
跑测试：
assert p2.degree() == 1023, f'The degree of the third constraint is {p2.degree()
} when it should be 1023.'
assert p2(31415) == 2090051528
print('Success!')
运行以下代码块观察约束多项式的次数，均小于 1024 。这在下一部分很重要。
print('deg p0 =', p0.degree())
print('deg p1 =', p1.degree())
print('deg p2 =', p2.degree())
步骤4 - 组合多项式
def get\_CP(channel):
alpha0 = channel.receive\_random\_field\_element()
alpha1 = channel.receive\_random\_field\_element()
alpha2 = channel.receive\_random\_field\_element()
return alpha0\*p0 + alpha1\*p1 + alpha2\*p2
跑测试：
test\_channel = Channel()
CP\_test = get\_CP(test\_channel)
assert CP\_test.degree() == 1023, f'The degree of cp is {CP\_test.degree()
} when it should be 1023.'
assert CP\_test(2439804) == 838767343, f'cp(2439804) = {CP\_test(2439804)
}, when it should be 838767343'
print('Success!')
提交组合多项式
最后，我们评估 cp 在评估定义域 (eval_domain) 上，在其上构建一棵 Merkle 树，并通过信道发送其根。 这类似于我们在第 1 部分末尾所做的 LDE 轨迹上的提交。
def CP\_eval(channel):
CP = get\_CP(channel)
return \[CP(d) for d in eval\_domain\]
在评估上构造一个默克尔树，并通过信道发送其根。
channel = Channel()
CP\_merkle = MerkleTree(CP\_eval(channel))
channel.send(CP\_merkle.root)
测试代码：
assert CP\_merkle.root == 'a8c87ef9764af3fa005a1a2cf3ec8db50e754ccb655be7597ead15ed4a9110f1', 'Merkle tree root is wrong.'
print('Success!')本文首发于：https://w3hitchhiker.mirror.xyz/atnvLVVSIexOf8iN57ZzAw4OS1f8tJLspyL44de2tTM
stark证明实操python实现03:<https://learnblockchain.cn/article/5493>
