EigenLayer 凭借 Restaking Points 成为 2024 开年最大黑马。项目的成功自然离不开技术的支撑，本文来解读其使用的独特验证签名方案——BLS 聚合签名。

以太坊中常用签名

在以太坊中，常用的是基于 secp256k1 曲线的 ECSDA 签名。每个 EOA 都由一对公私钥组成，私钥对消息摘要进行签名，利用对应的公钥验证签名。 在 Solidity 合约中，我们可以使用 ecrecover 关键字对消息摘要以及签名的 v,r,s 进行验签，还原出签名者地址。

ECDSA 的弊端

要知道，签名的验证操作会大量消耗 gas ( 0x01 预编译合约 ecRecover 至少消耗 3000 gas)，验证一次签名只能确认一个账户的身份，所以当一笔交易中要验证大量账户时，使用 ECDSA 就容易拉高成本甚至超过最大 Gas Limit

EigenLayer 选择聚合签名

EigenLayer 有大量的节点运营商(AVS)，他们需要对接受的数据进行验证和确认，最后提交的自己的签名用以证明。 为了避免一个个地去验证签名，EigenLayer 选择了将多个签名聚合成一个，进而只需要验证一次签名来提高效率。

BLS 聚合签名原理

核心概念：“曲线哈希”与“曲线配对”

曲线哈希

在 ECDSA 签名算法中，我们对消息进行哈希计算后，结果（哈希值）是数字。BLS 签名算法则不同，它略微修改了哈希算法，结果对应到椭圆曲线上（的一个点）。

曲线配对

需要一个特殊的函数，能够把一条（或2条不同的）曲线上的两个点 P 和 Q 映射为一个数：$e(P, Q) → n$

此函数还要有一个重要的特性。即对于未知数 x 和两个点 P 、 Q ，无论哪个点乘以 x，结果相同，即 $$ e(x*P, Q) = e(P, x*Q) $$

如此，除了乘数交换仍能保持等式成立外，更进一步，以下所有的交换都要保持等式成立： $$ e(a*P, b*Q) = e(P, ab*Q) = e(ab*P, Q) = e(P, Q)^(ab) $$

其背后的数学原理相当复杂，具体细节参考文章

签名方案

我们用 pk 代表私钥，$P = pk*G$ 代表公钥，m 代表要签名的消息。

为了计算签名，先对消息求曲线哈希 H(m) ，再将获取的结果（曲线坐标点）乘以私钥即可: $S = pk*H(m)$ 。签名结果是一个曲线上的点，用压缩的序列化格式保存，只占 33 个字节。

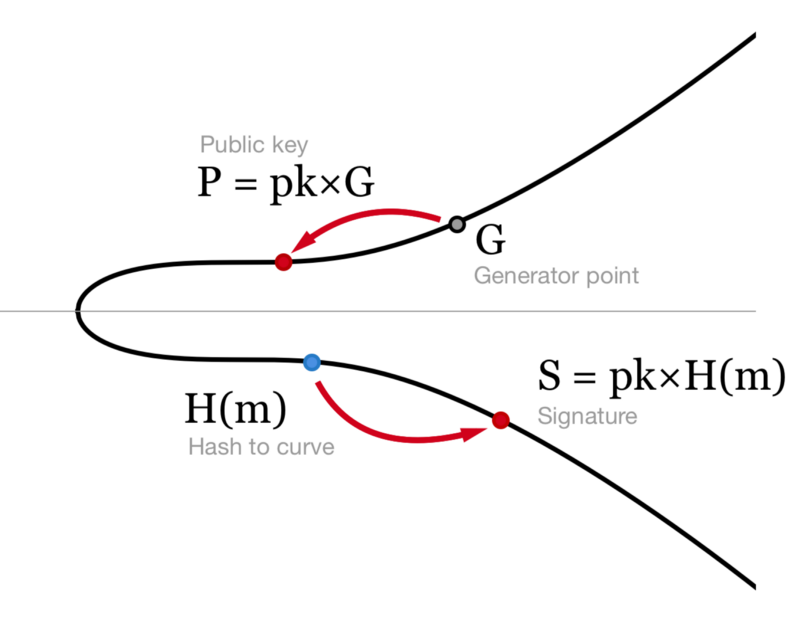
生成 BLS 签名。就是将消息的哈希结果乘以私钥。

可以使用公钥 P 来验证签名，即 $e(P, H(m)) = e(G, S)$ ，推倒如下：

如前所述，配对函数的特性使得如下等式成立

$$ e(P, H(m)) = e(pk*G, H(m)) = e(G, pk*H(m)) = e(G, S) $$

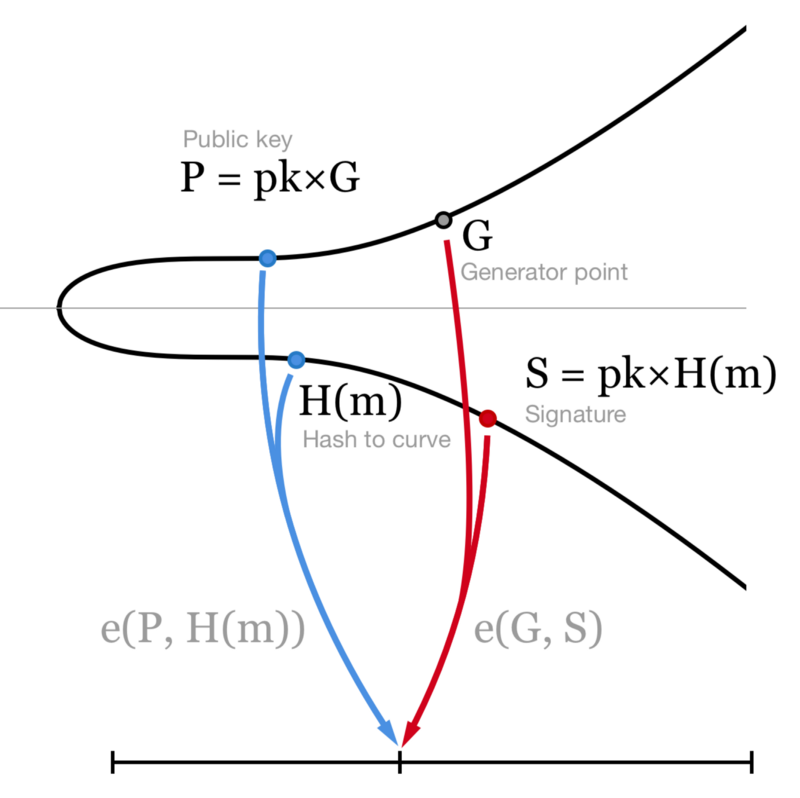
BLS 签名的验证。我们只需验证公钥和消息的哈希值（图中蓝色的两个点） 与曲线生成点和签名（图中红色的两个点） 是否映射到同一个数，若是则说明这是一个有效的 BLS 签名。

聚合

假设一个区块中有 1000 笔交易，每笔交易都由 Si（签名），Pi （公钥）和 mi（消息）组成（i 在这里表示序号）。为获得聚合签名，只需要将区块中的所有签名加起来：

$$ S = S1 + S2 +…+ S1000 $$

为验证该签名正确，我们需要保证以下等式成立：

$$ e(G, S) = e(P1, H(m1)) * e(P2, H(m2)) *…* e(P1000, H(m1000)) $$

如果签名都有效，那么该等式的确是成立的：

$$ e(G, S) = e(G, S1+S2+…+S1000) = e(G, S1) × e(G, S2) *…* e(G, S1000) = e(G, pk1×H(m1)) *…* e(G, pk1000×H(m1000)) = e(pk1×G, H(m1)) *…* e(pk1000×G, H(m1000)) = e(P1, H(m1)) × e(P2, H(m2)) *…* e(P1000, H(m1000)) $$

也就是说聚合签名有效就代表着聚合的每个签名都有效。

合约实现

EigenLayer 的合约代码十分庞大复杂，我将其中最典型的 BLS 签名校验抽离出来放在这个 repo 里。

主合约只有不到 100 行代码，实现了将所有公钥聚合成 apk (聚合公钥) 并对聚合签名进行曲线配对验证。

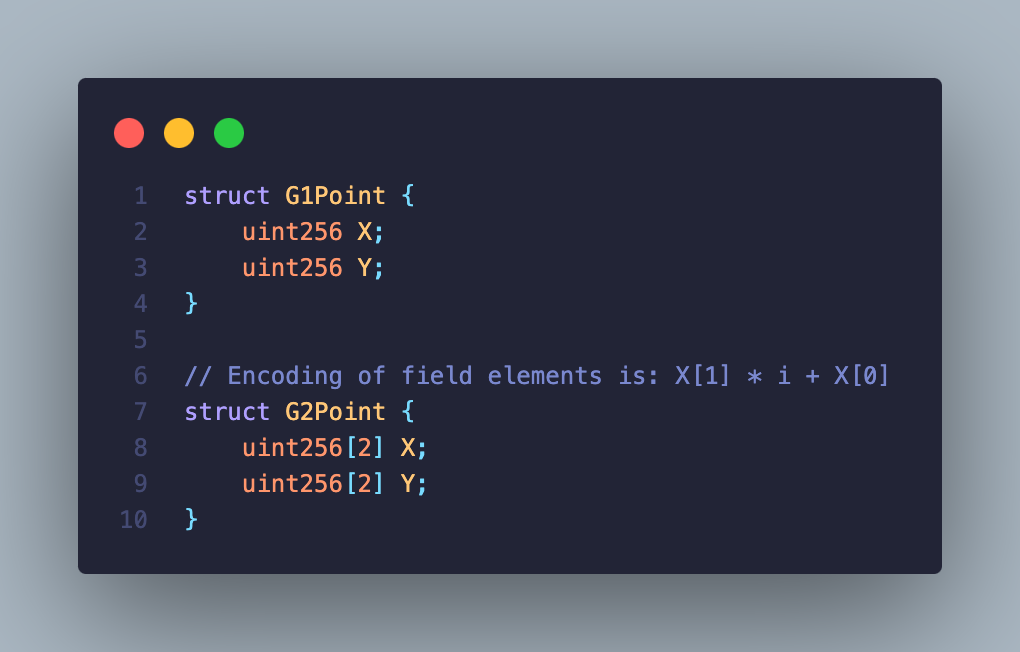
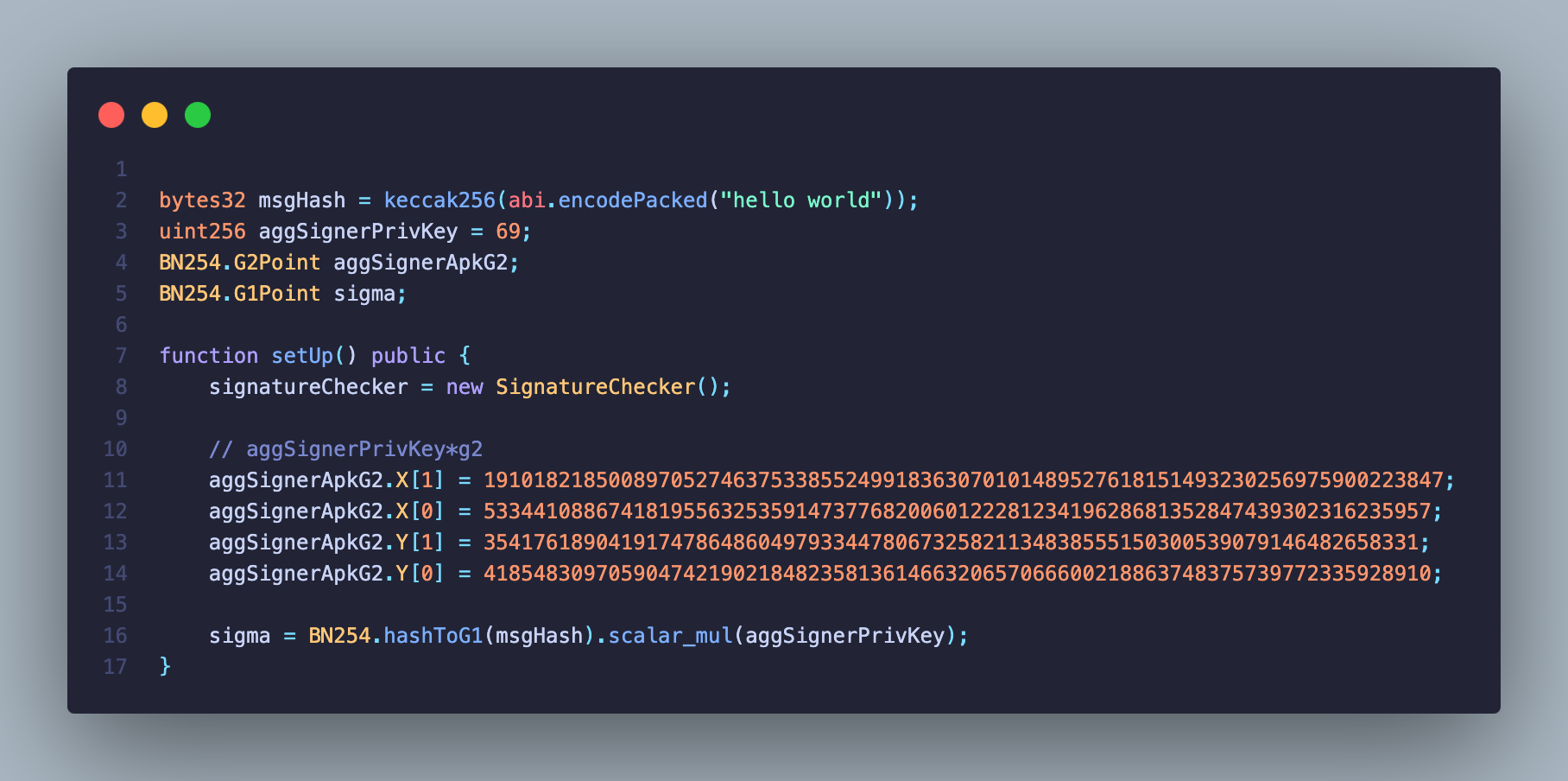
使用的 BLS 签名方案基于 BN254 椭圆曲线，实现为 BN254 library 合约，定义了 G1 (一维) , G2 (二维) 两种坐标格式

公钥的聚合是曲线向量加和

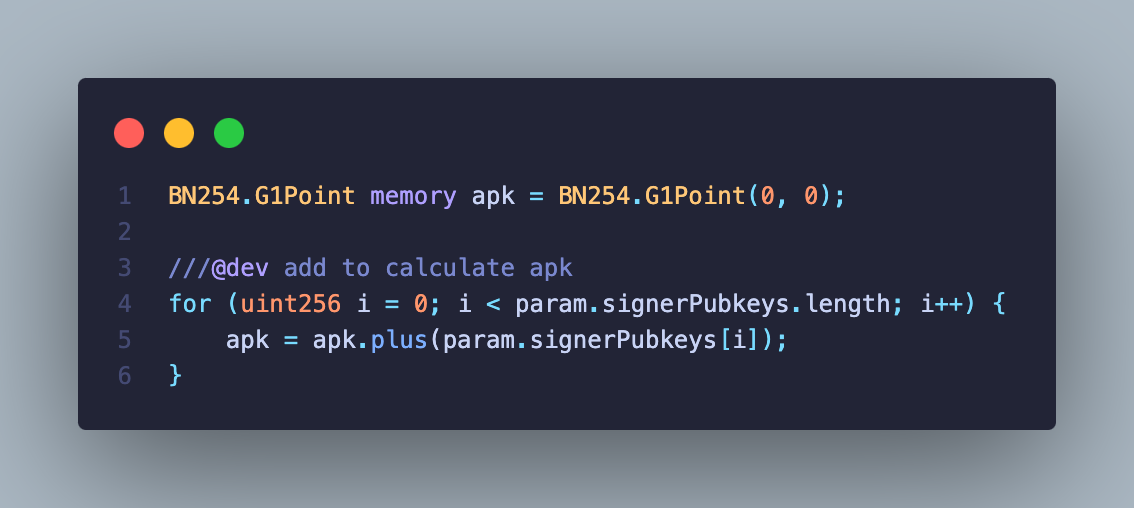
依靠 0x06 预编译合约 ecAdd 来实现曲线向量和

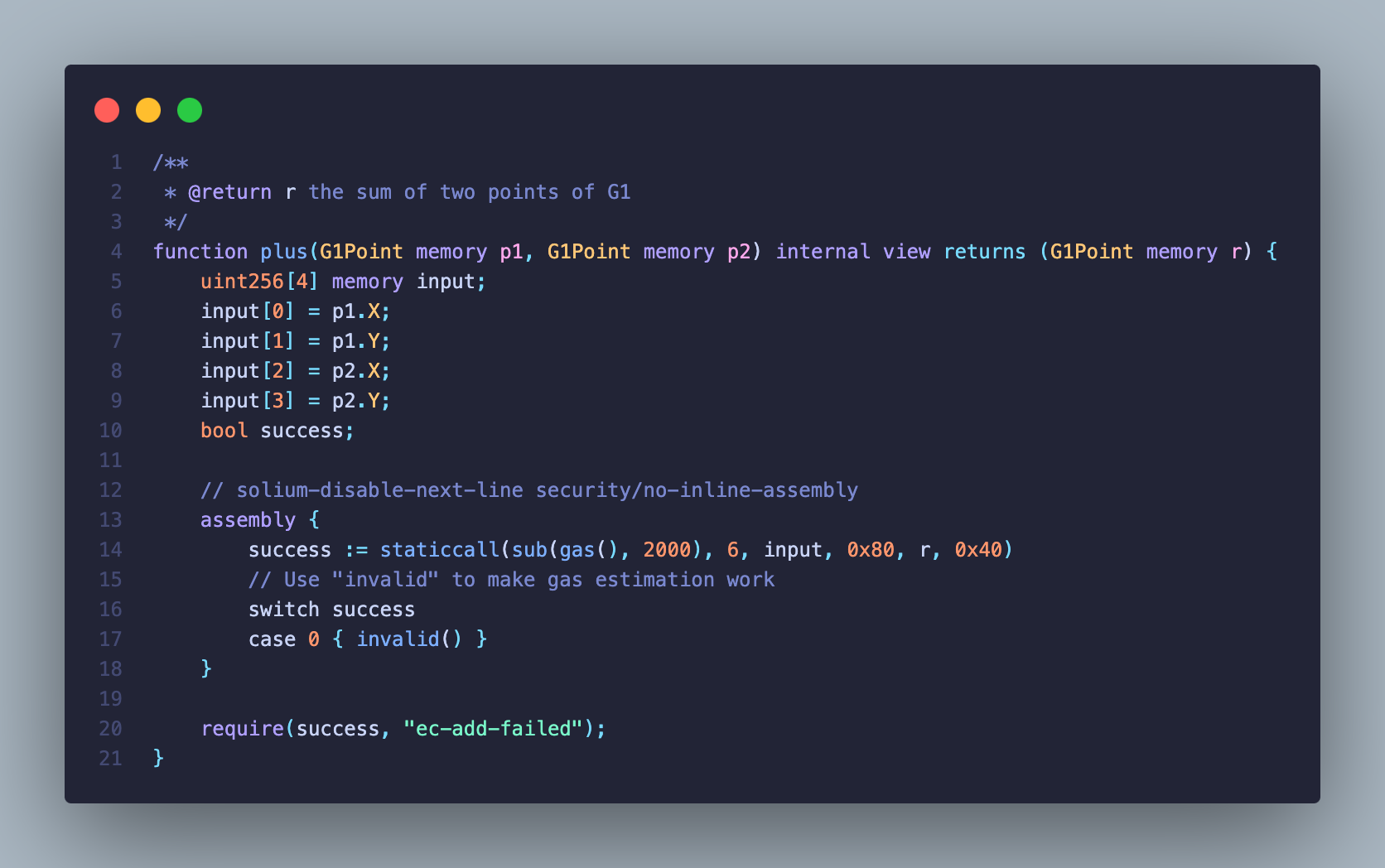
聚合签名是则将消息摘要和聚合私钥(标量)相乘

借助了 0x07 预编译合约 ecMul 求积

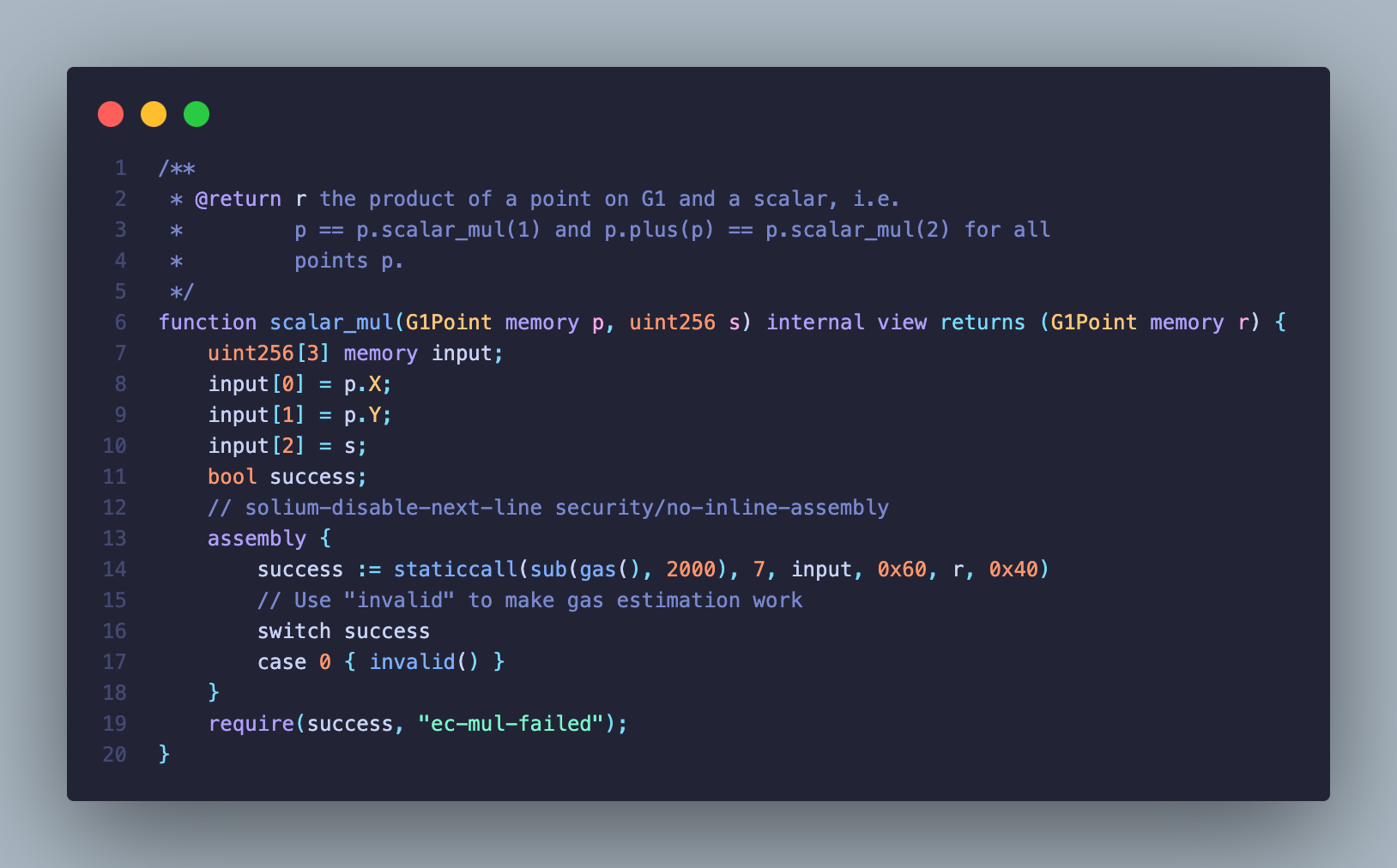
最后使用 safePairing 函数来校验是否配对成功和签名有效

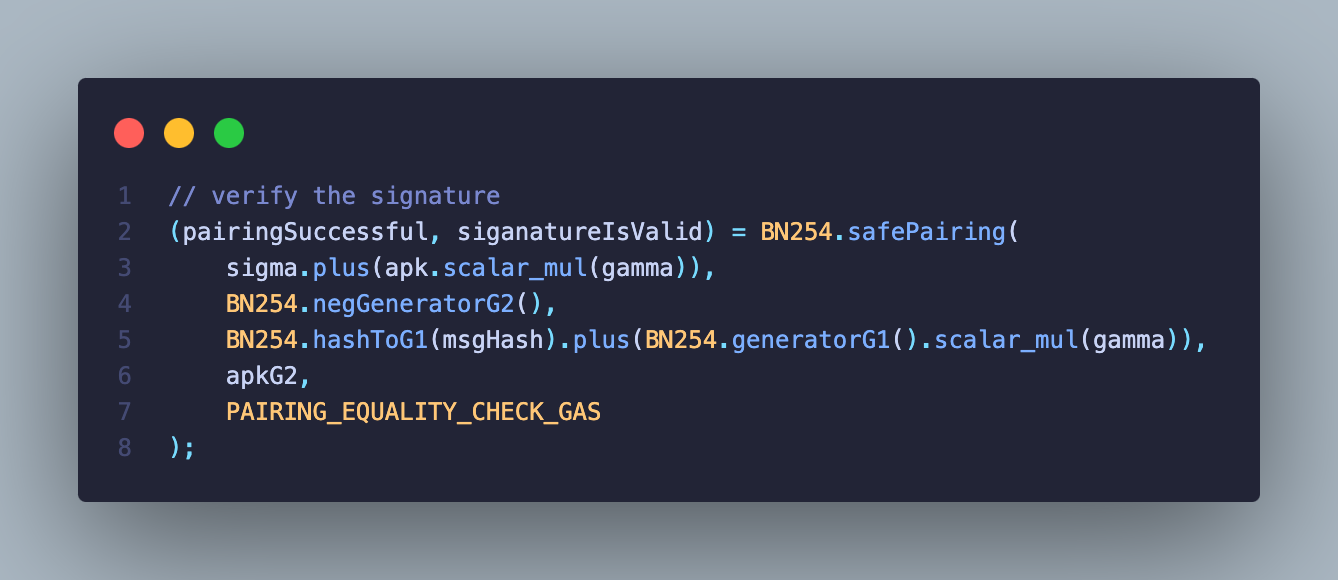
借助 0x08 预编译合约 ecPairing 来验证

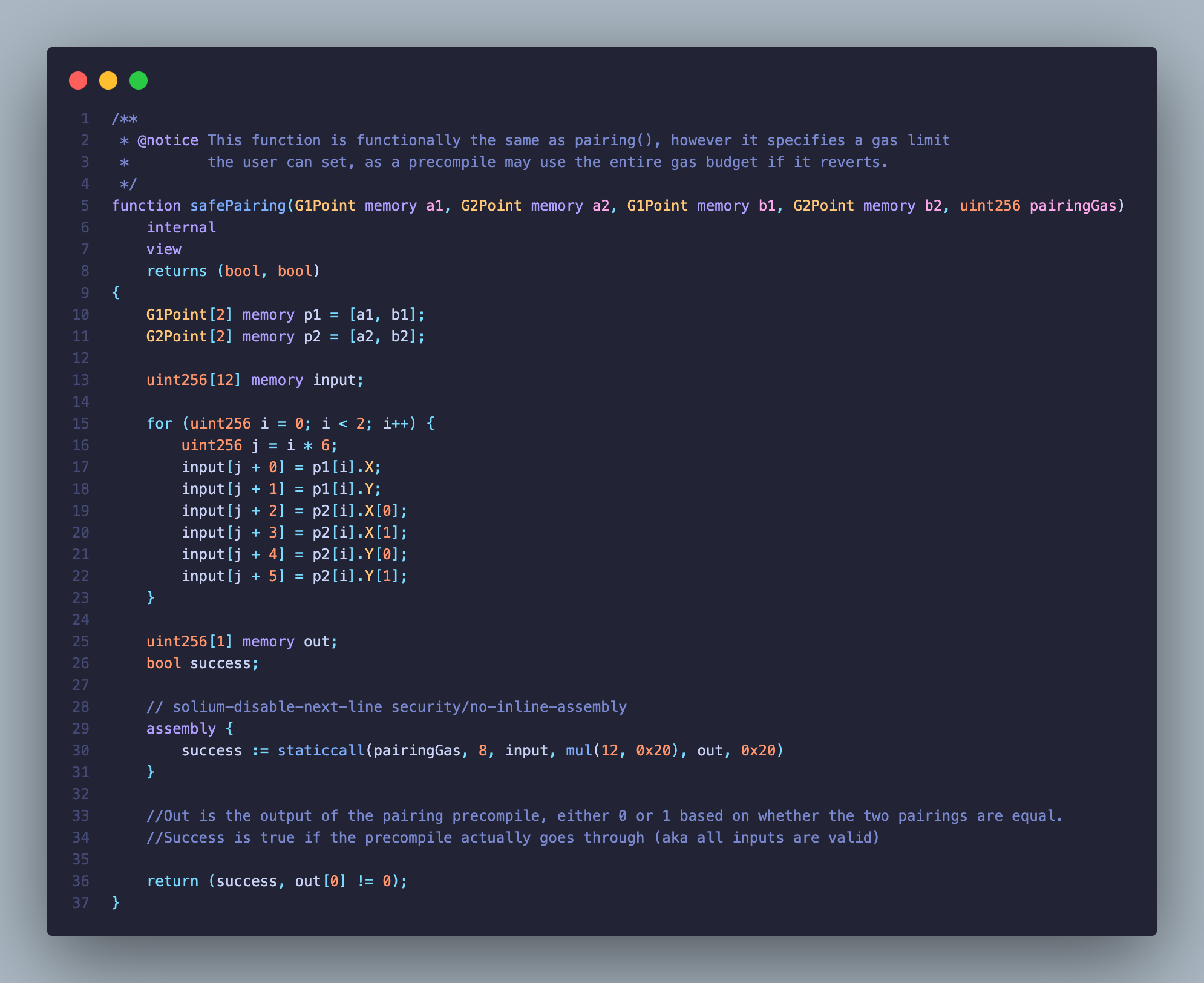
一次曲线配对至少消耗 45000 gas 相当于 15 次 ECDSA 验签，然而实际中一次需要校验的签名数量往往 100 个起步，所以能节省大量的 gas 和时间

总结

BLS 签名方案通过聚合签名和公钥，提高签名验证速度的同时还节省了成本。 近日V神在香港的演讲中也表达了对 BLS 聚合签名的看好。