FHE全同态加密介绍——小白版
- mutourend
- 发布于 2024-06-28 22:18
- 阅读 4982
FHE全同态加密介绍——小白版
1. 何为FHE?
FHE中的evluation key $pk_{eval}$是public的,用于密文计算逻辑$f(\cdot)$的evalute circuit中,但根据所处理数据加解密密钥的不同,可将FHE分为:
- 1)对称FHE:即对数据的加解密密钥$sk$是相同的,都是secret的,与AES对称加密类似。
- 2)非对称FHE:即对数据加密采用公钥$pk$,解密采用私钥$sk$。
- 非常实用,支持多人贡献数据(使用公钥$pk$加密),而仅,拥有私钥$sk$的人可解密。
- 借助不同于(如RSA、Elgamal等)常规加密算法的polymorphic encryption,使得对称FHE和非对称FHE,二者等价,可相互转换。
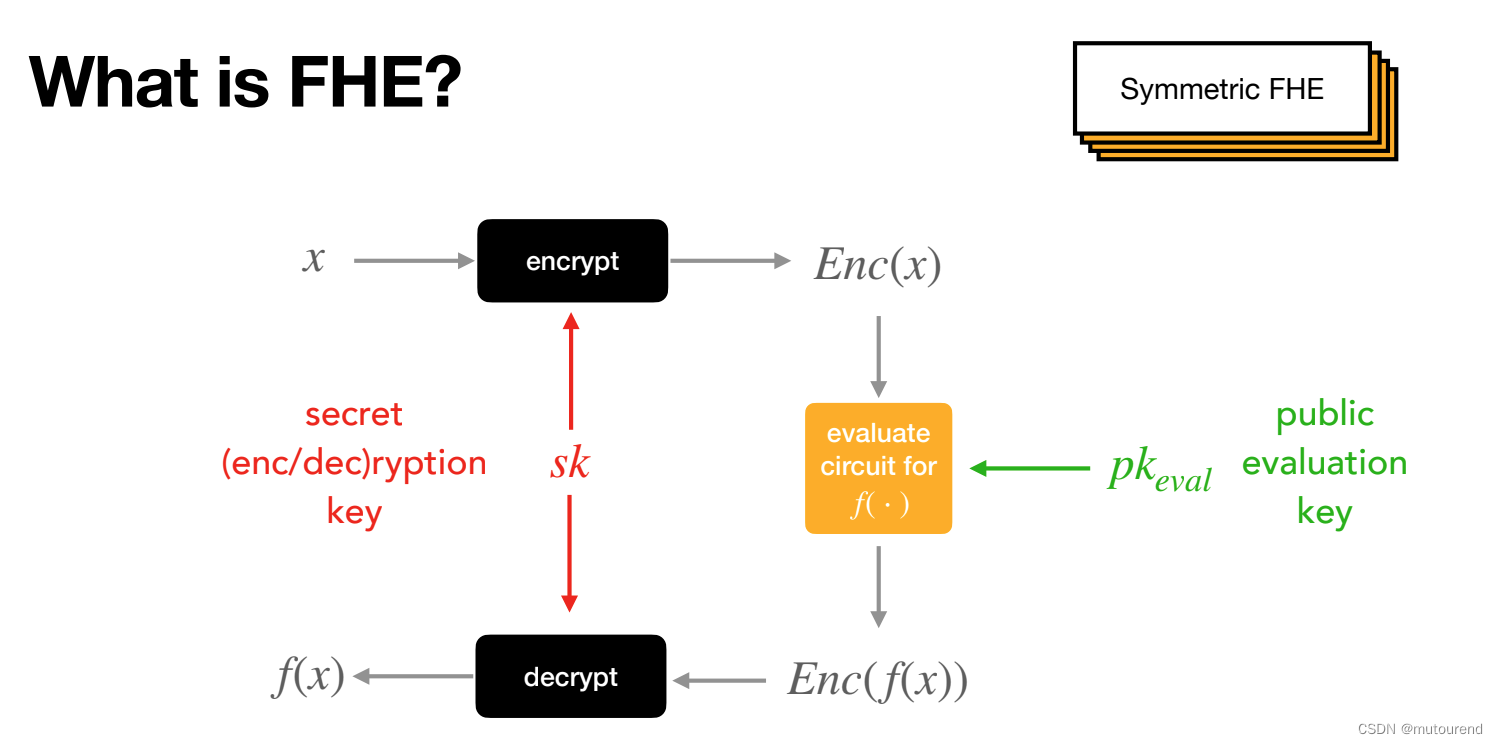
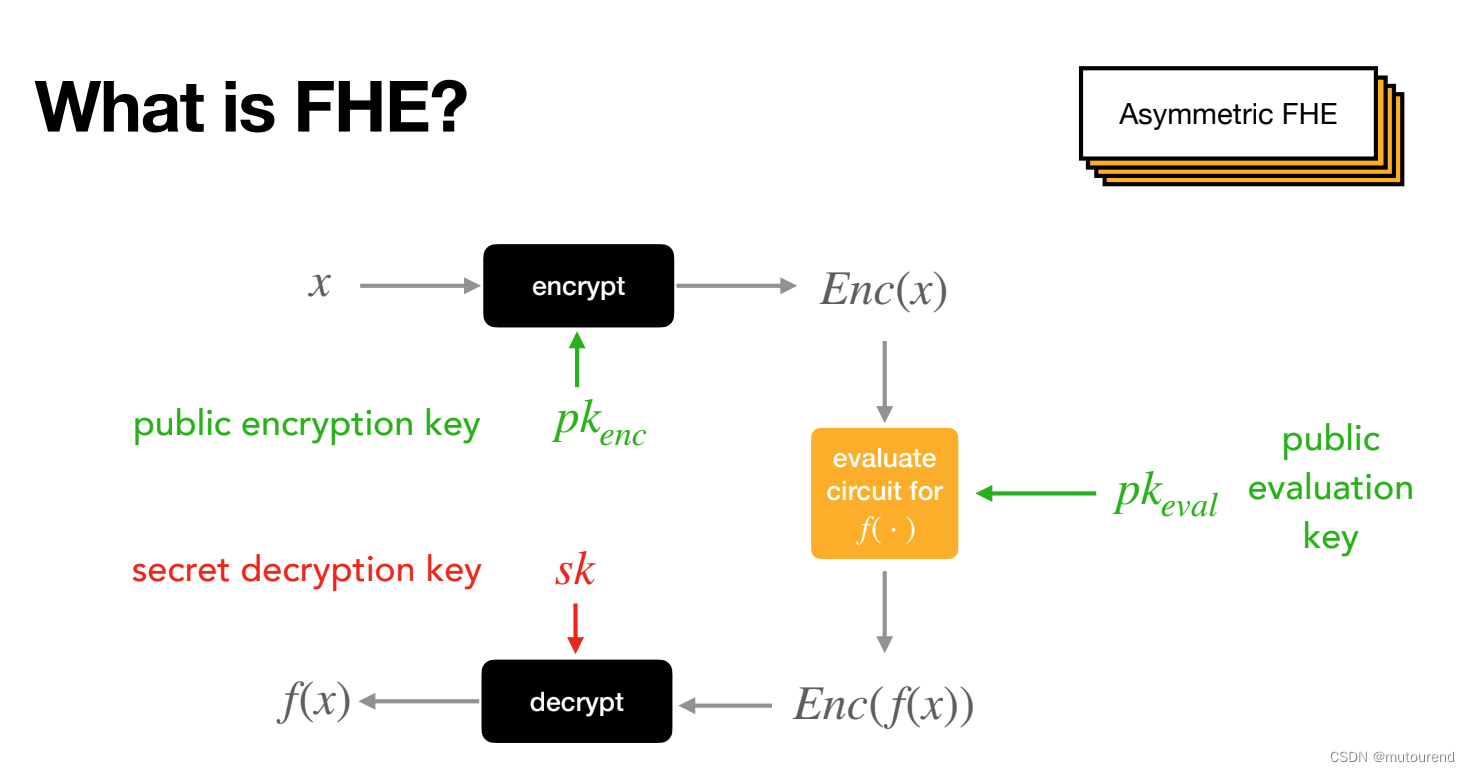
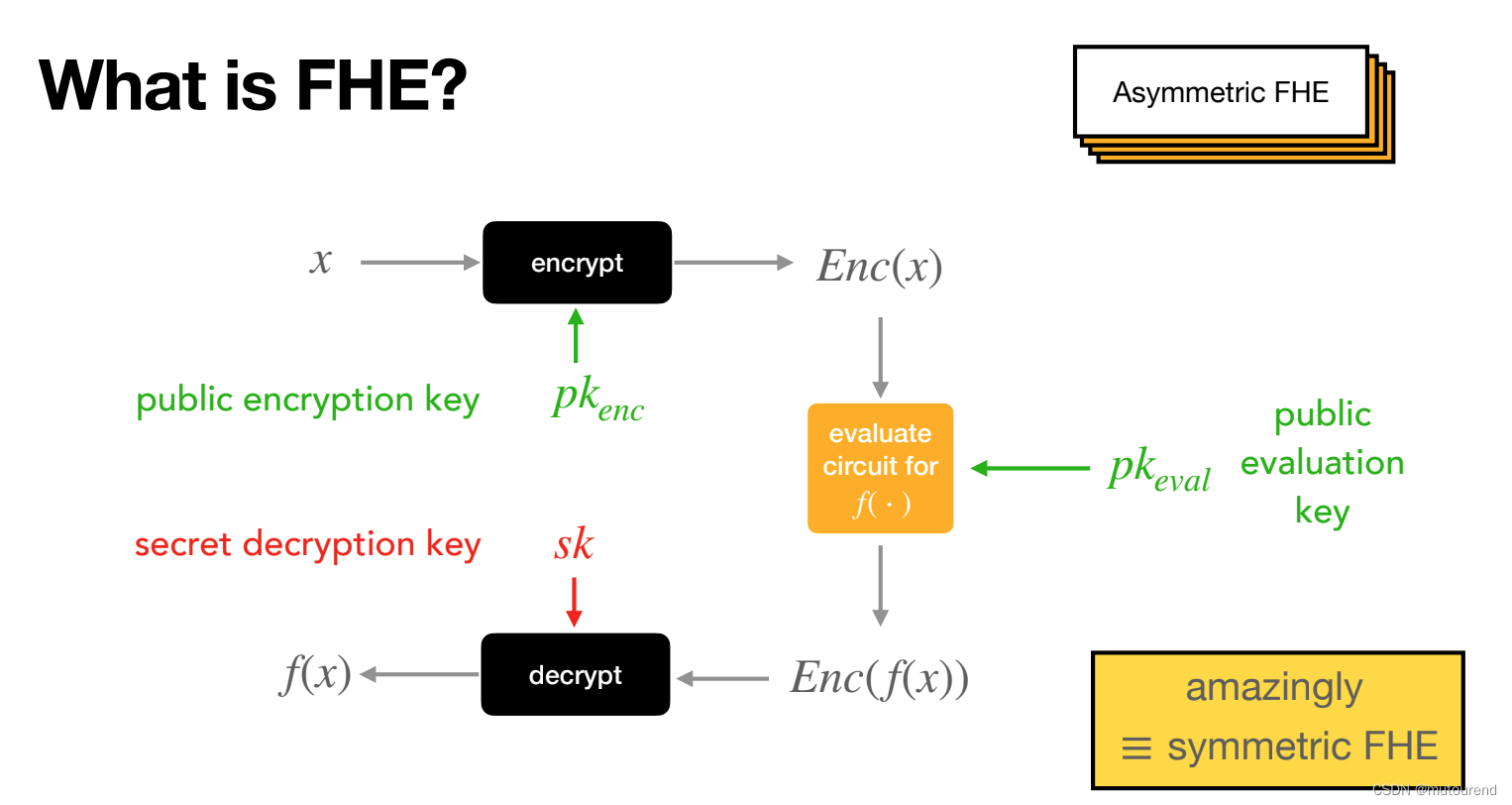
全同态加密(FHE):
- 可防止数据盗窃和监视,使localization(本地化)变得不必要。
- 数据在传输和处理过程中,都是端到端加密的。
- FHE使数据能够在处理过程中始终保持加密,使公司能够在不访问用户数据的情况下提供服务。由于没有政府或黑客能够解密服务端数据,本地化变得不必要,这使公司节省了大量的云基础设施成本。
- FHE调和了网络隐私,高效FHE将有助于从https://,大幅迈进httpz://。【让用户真正具有数据主权和隐私权。】
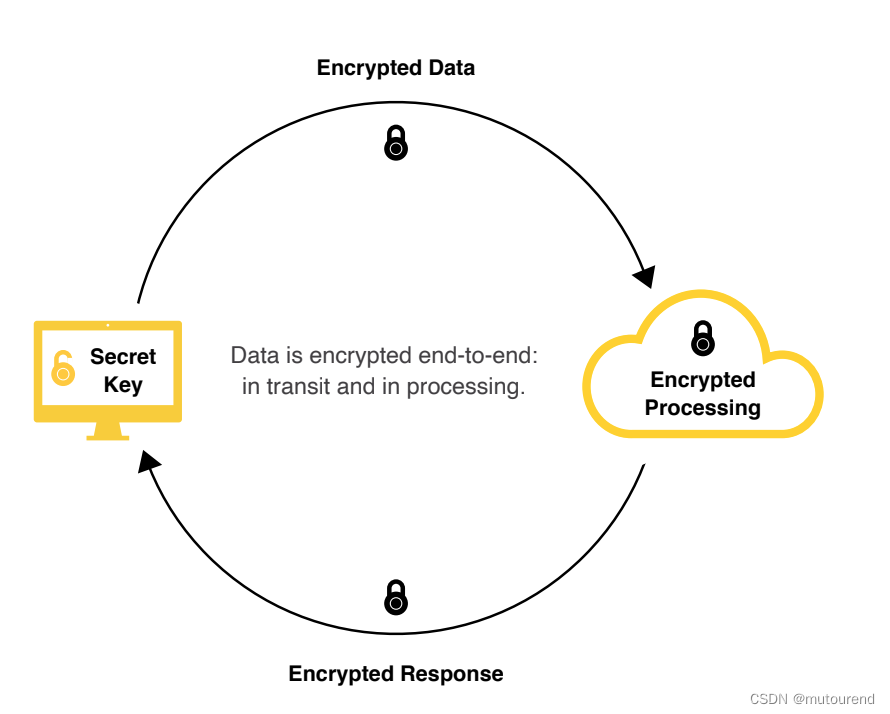

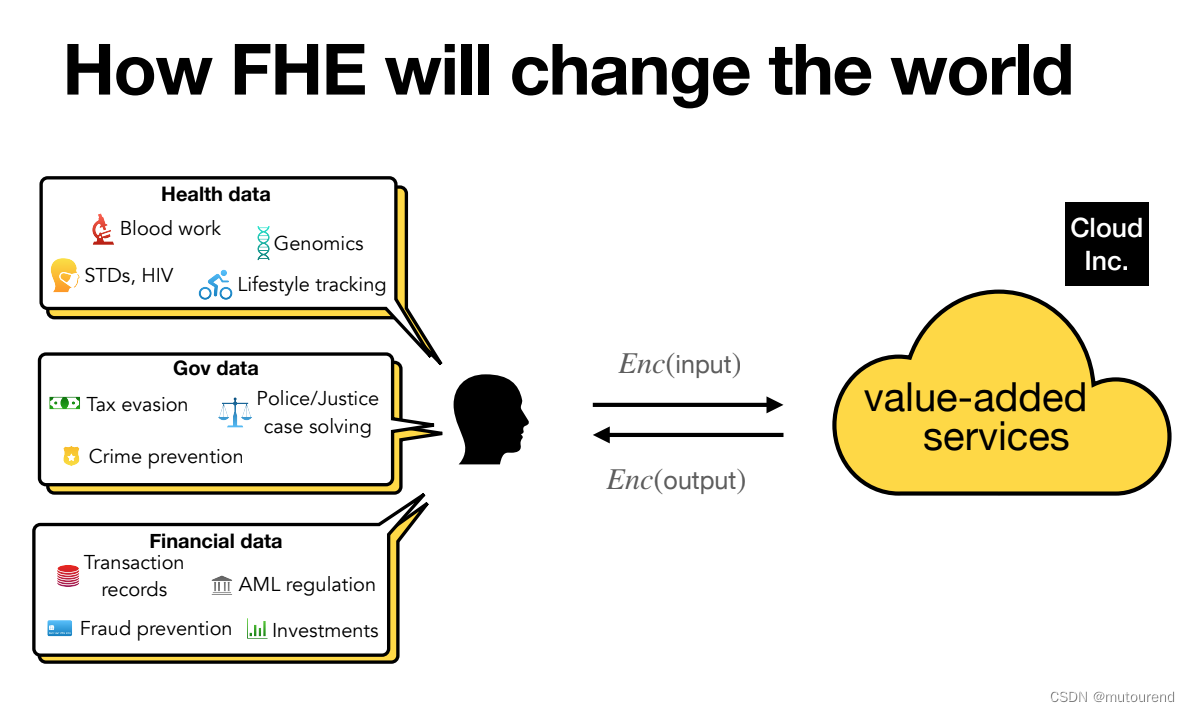
FHE将改变现有数据管理和处理范式:
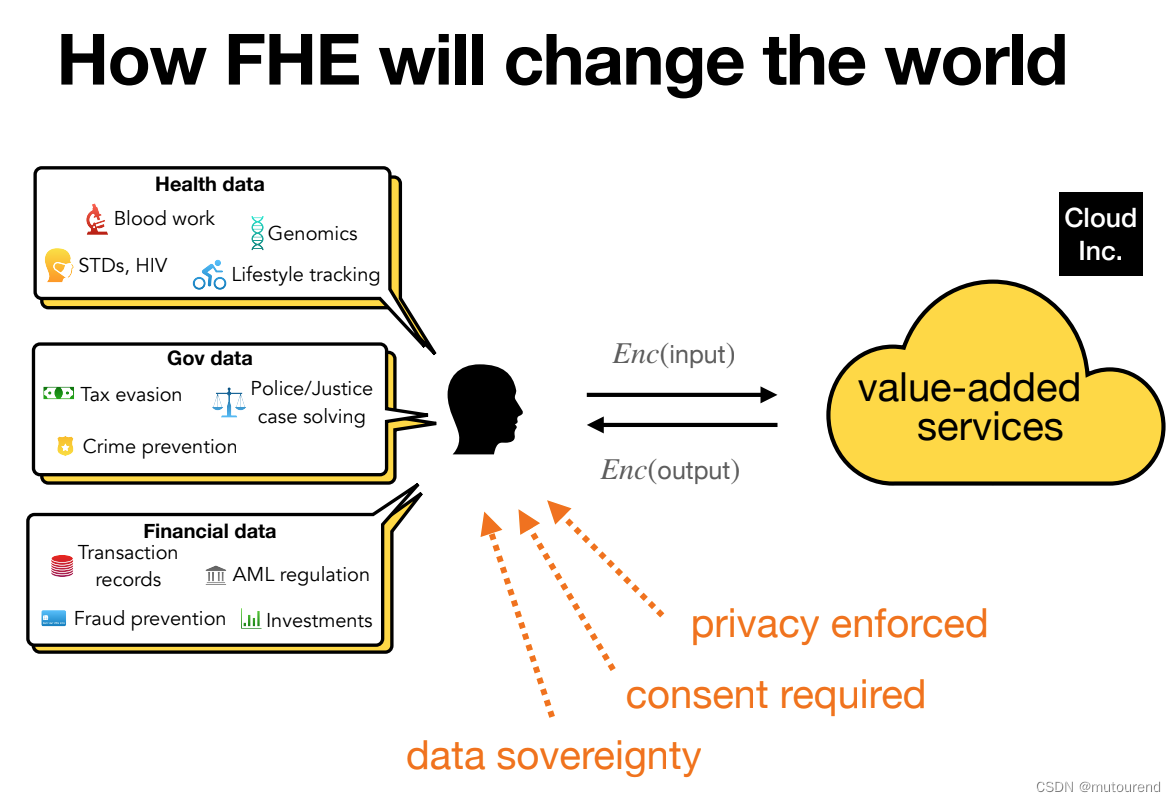
- 用户个人所持有的健康数据、纳税等政府数据、投资等金融数据,是以密文形式发送给增值服务处理的。对于用户,借助FHE技术,可:
- 强化用户数据隐私
- 需获得用户许可
- 用户真正拥有数据主权
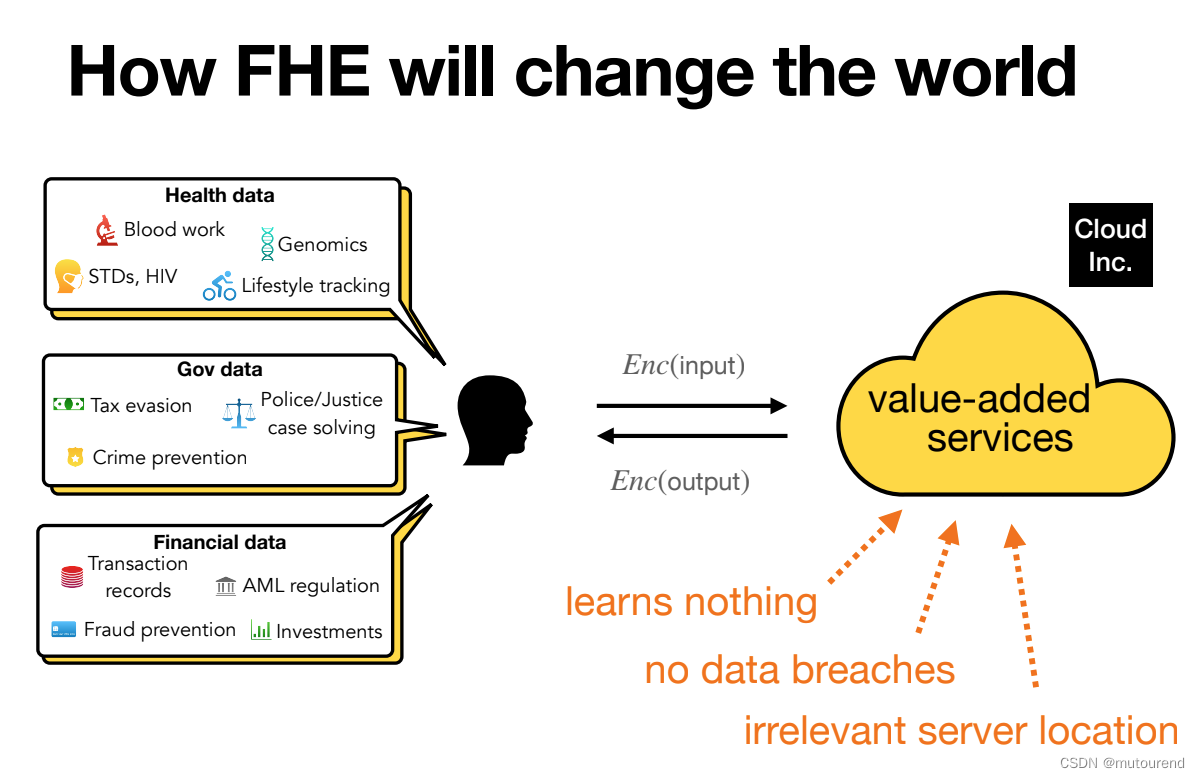
- 对于提供增值服务的提供商,若采用FHE技术:
- 无法获悉用户数据的明文信息
- 无数据泄露风险
- 与服务部署位置无关,可使用云服务,使本地化变得无必要。
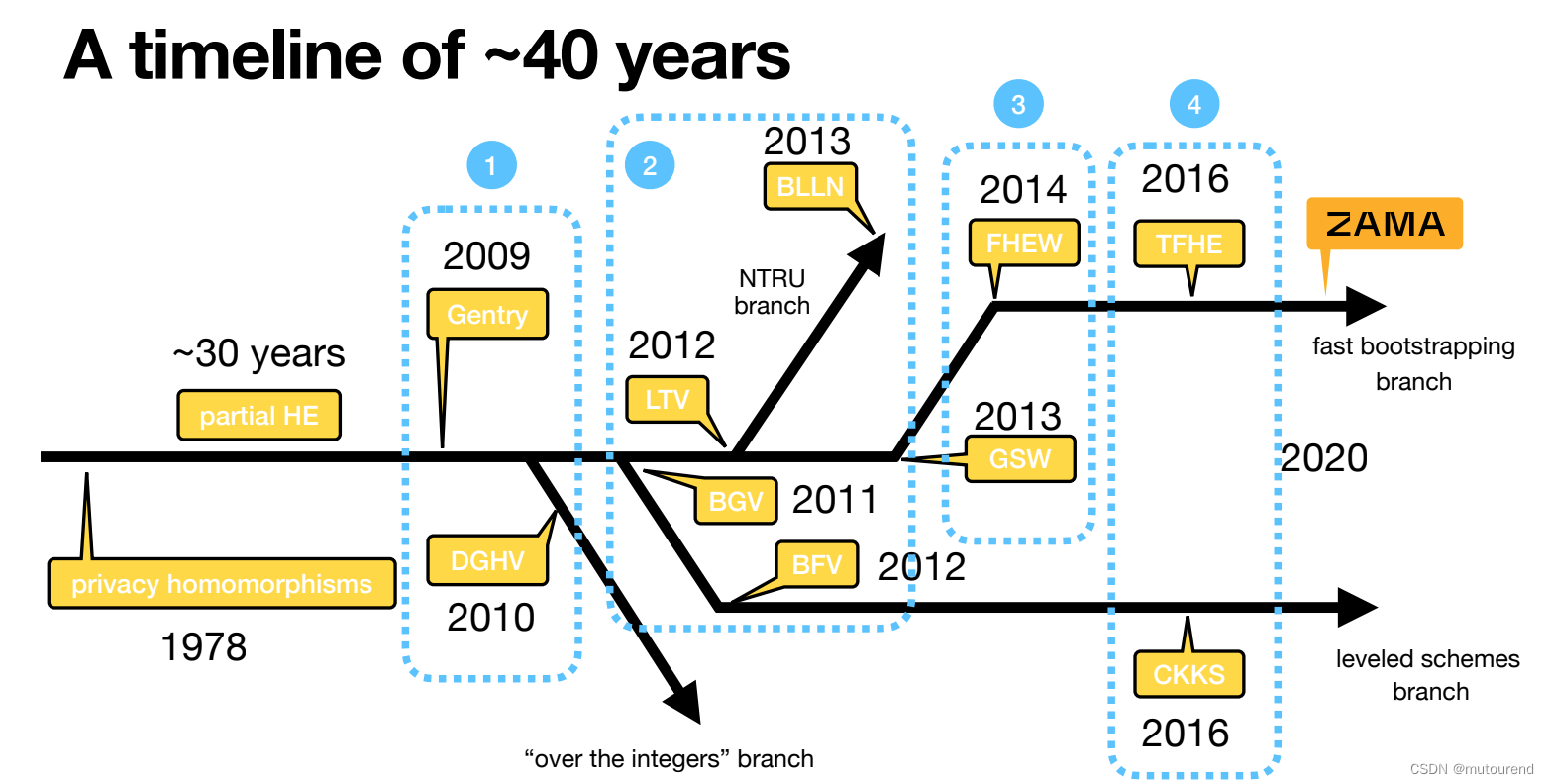 过去四十多年来,FHE的衍化可分为4代:
过去四十多年来,FHE的衍化可分为4代:
- 第一代FHE:代表作为2009年Gentry和2010年DGHV。【均为“基于整数”分支】
- 第二代FHE:代表作为2011年BGV、2012年LTV、2012年BFV(属leveled schemes分支)、2013年BLLN(属NTRU分支)。
- 第三代FHE:代表作为2013年GSW、2014年FHEW(属fast bootstrapping分支)。
- 第四代FHE:代表作为2016年CKKS(属leveled schemes分支)、2016年TFHE(属fast bootstrapping分支)。
2. 第一代FHE
第一代FHE:代表作为2009年Gentry和2010年DGHV。【均为“基于整数”分支】
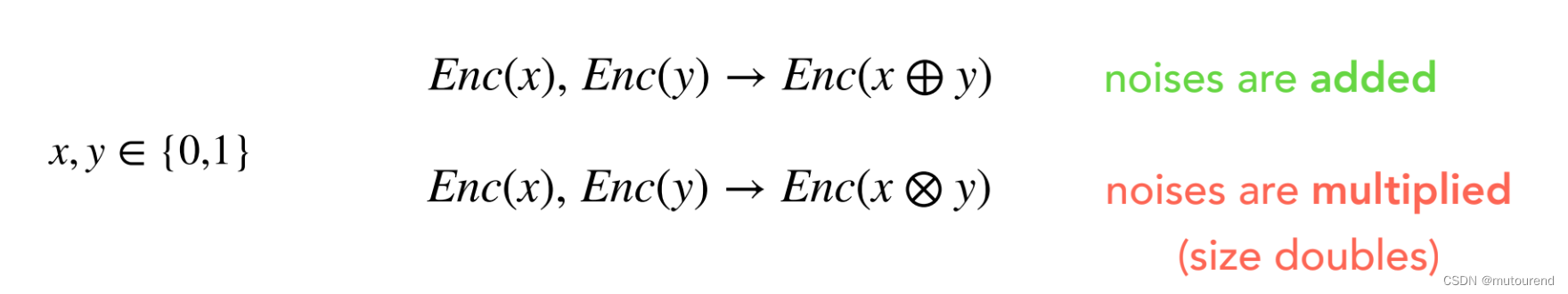 明文数据为:
明文数据为:
- $x,y\in{0,1}$
对应有:
- 加法同态运算:根据密文$Enc(x),Enc(y)$,可计算出$Enc(x\oplus y)$。加法同态运算很快。【噪声是相加的】
- 乘法同态运算:根据密文$Enc(x),Enc(y)$,可计算出$Enc(x\otimes y)$。乘法同态运算很慢。【噪声是相乘的,噪声长度将翻倍。】
由于明文为二进制数据,其中:
- $\oplus=+ \mod 2=xor$
- $\otimes=\times \mod 2=and$
对应的FHE电路为boolean电路:
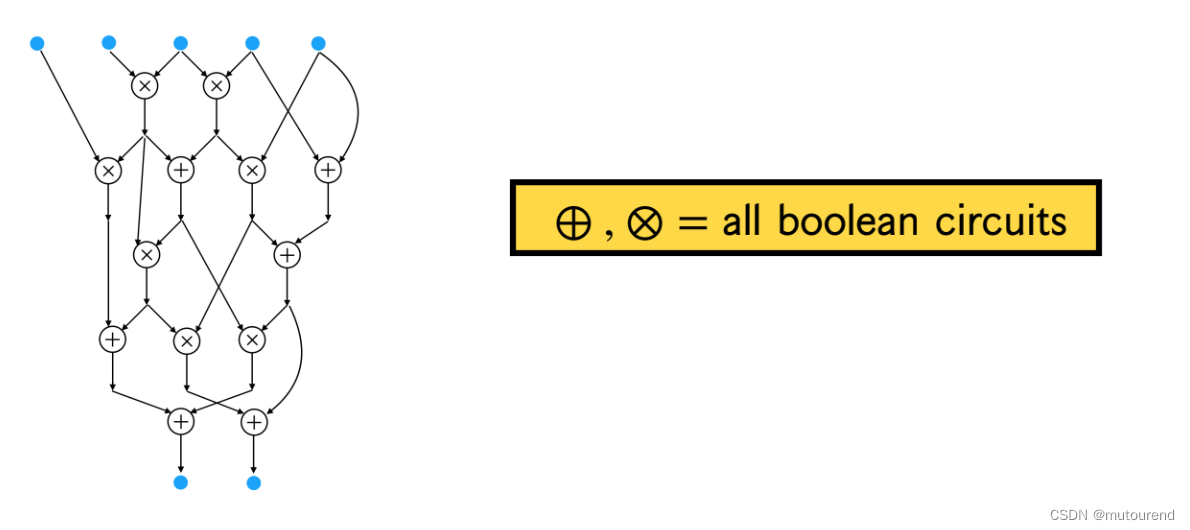 但是用于FHE计算的密文数据中,存在噪声(noise)的概念,且:
但是用于FHE计算的密文数据中,存在噪声(noise)的概念,且:
- 噪声会随时间累积:
- 对于加法运算,两个密文的噪声是相加的。
- 对于乘法运算,两个密文的噪声是相乘的。最终的噪声长度将翻倍。
- 当噪声一定水平时,密文可正确被解密;当噪声高于一定水平时,则解密结果不正确。

由于乘法运算的噪声是相乘的,最终的噪声长度按翻倍增长,则意味着:
- 乘法运算的噪声,将随其深度,呈指数增长。
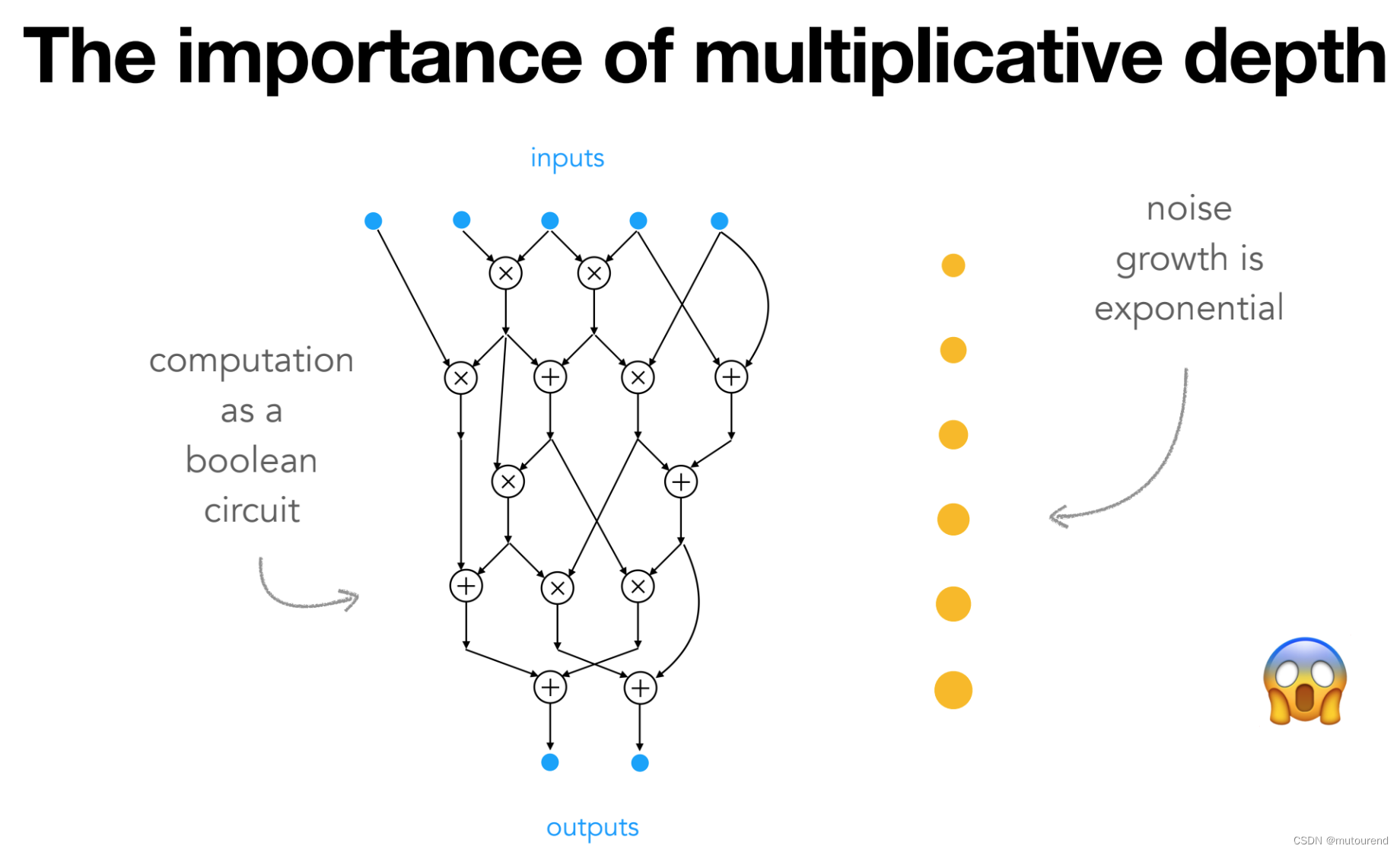 这就意味着,少量的乘法运算,噪声就会淹没密文数据,即以上FHE方案本质为SHE方案(Somewhat homomorphic encryption,即只支持有限次数的乘法运算)。为解决SHE方案中噪声呈指数增长的问题,Gentry提出了一种巧妙的思路——引入了:
这就意味着,少量的乘法运算,噪声就会淹没密文数据,即以上FHE方案本质为SHE方案(Somewhat homomorphic encryption,即只支持有限次数的乘法运算)。为解决SHE方案中噪声呈指数增长的问题,Gentry提出了一种巧妙的思路——引入了:
- bootstrapping自举。如下图所示的自举方案,尽管可以降噪,但存在的问题在于,该自举计算非常慢。
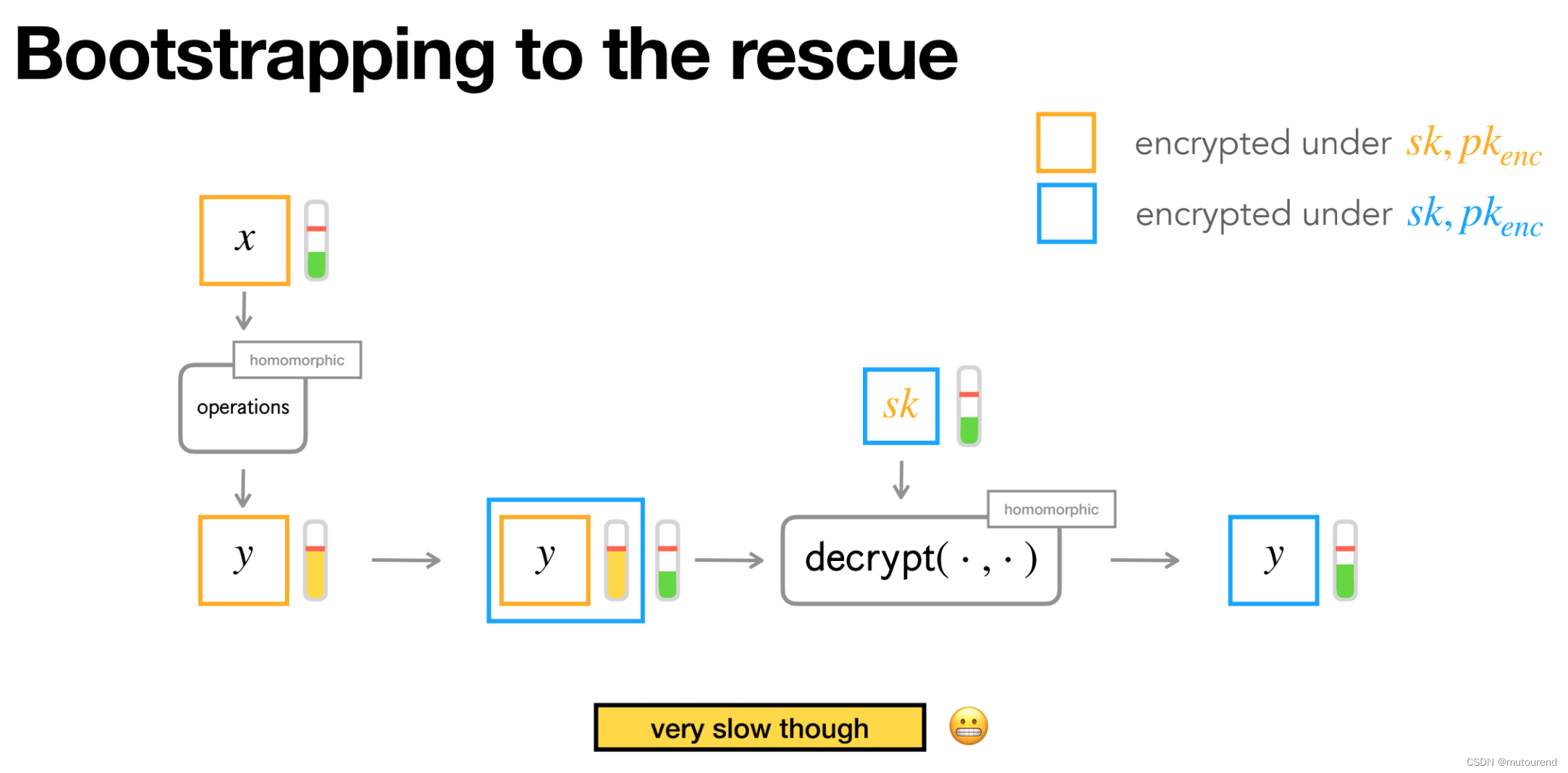
但借助上图的bootstrapping自举方案,可做任意深度的乘法运算,即可实现无限次数的乘法运算——称为initial FHE vision,与之前的SHE方案对比为:
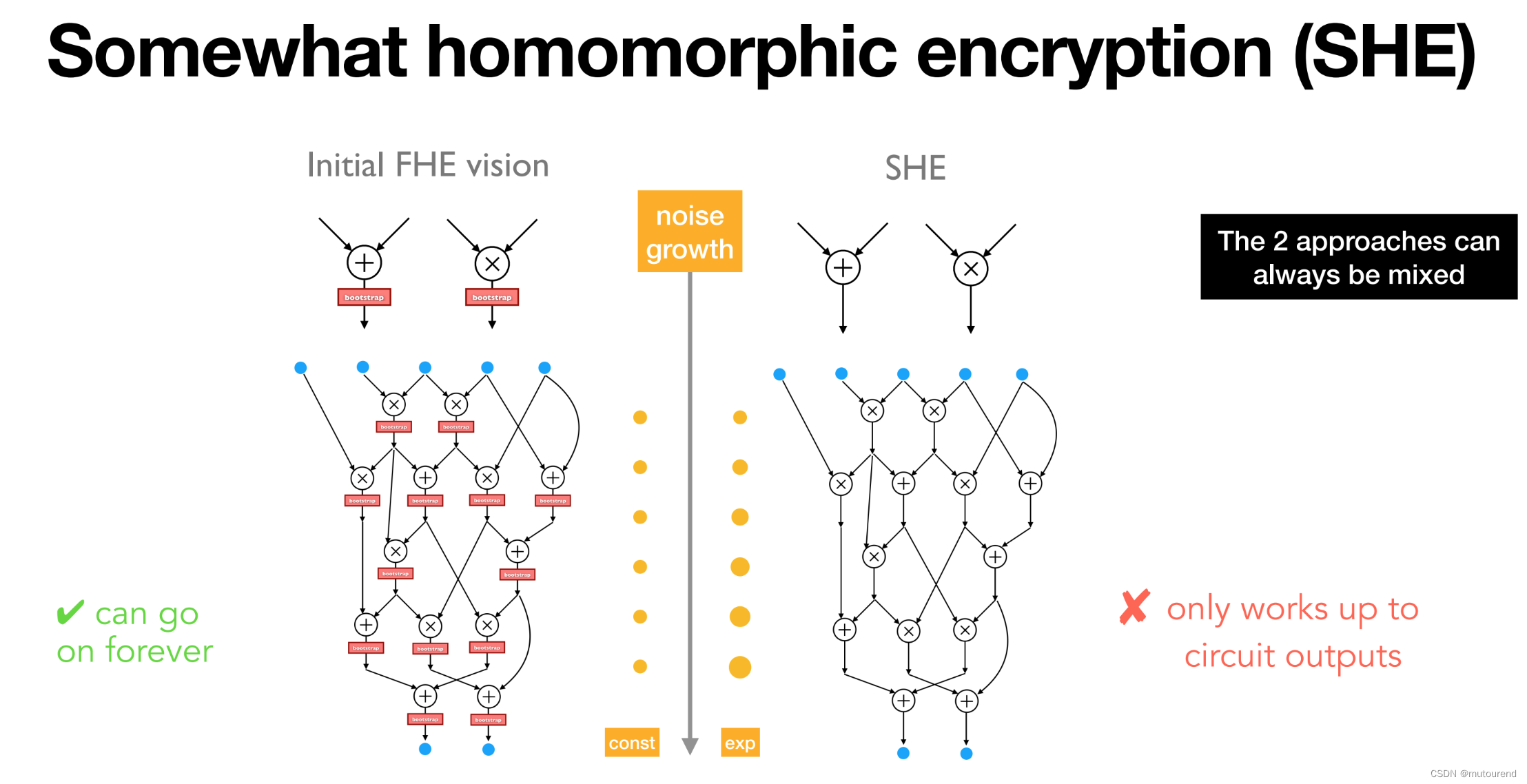 其中:
其中:
- initial FHE vision中的噪声呈常量增长:可支持任意次数乘法运算。
- SHE方案中的噪声呈指数增长:仅支持有限次数乘法运算。
- initial FHE vision 和 SHE方案,可混合使用。
3. 第二代FHE
第二代FHE:代表作为2011年BGV、2012年LTV、2012年BFV(属leveled schemes分支)、2013年BLLN(属NTRU分支)。
第二代FHE中,开始出现属于leveled schemes分支的FHE方案:2012年BFV。
所谓leveled schemes分支的FHE方案,是指:
- 密文具有的噪声level为:$\ell\in{1,\cdots,L}$
- 2个密文加法运算后的噪声level为:取2个输入密文的最大噪声level。
- 2个密文乘法运算后的噪声level为:取2个输入密文的最大噪声level,再加$1$。
- 若密文的噪声level为$L+1$,则意味着该密文将无法被正确解密。
- 噪声level为$L$时,可通过bootstrapping,将噪声level降为$1$。
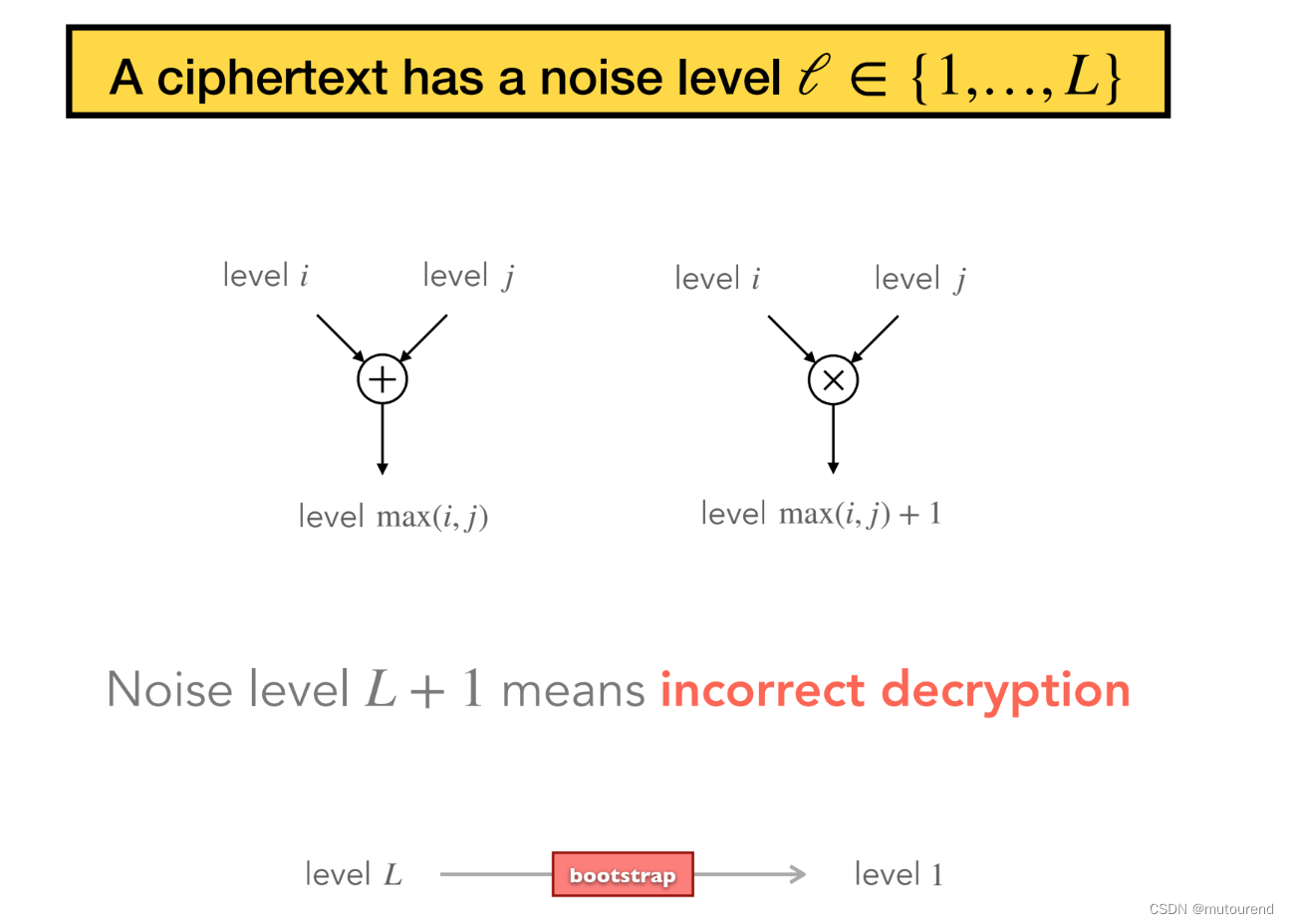 这即意味着,leveled schemes分支中的FHE方案:
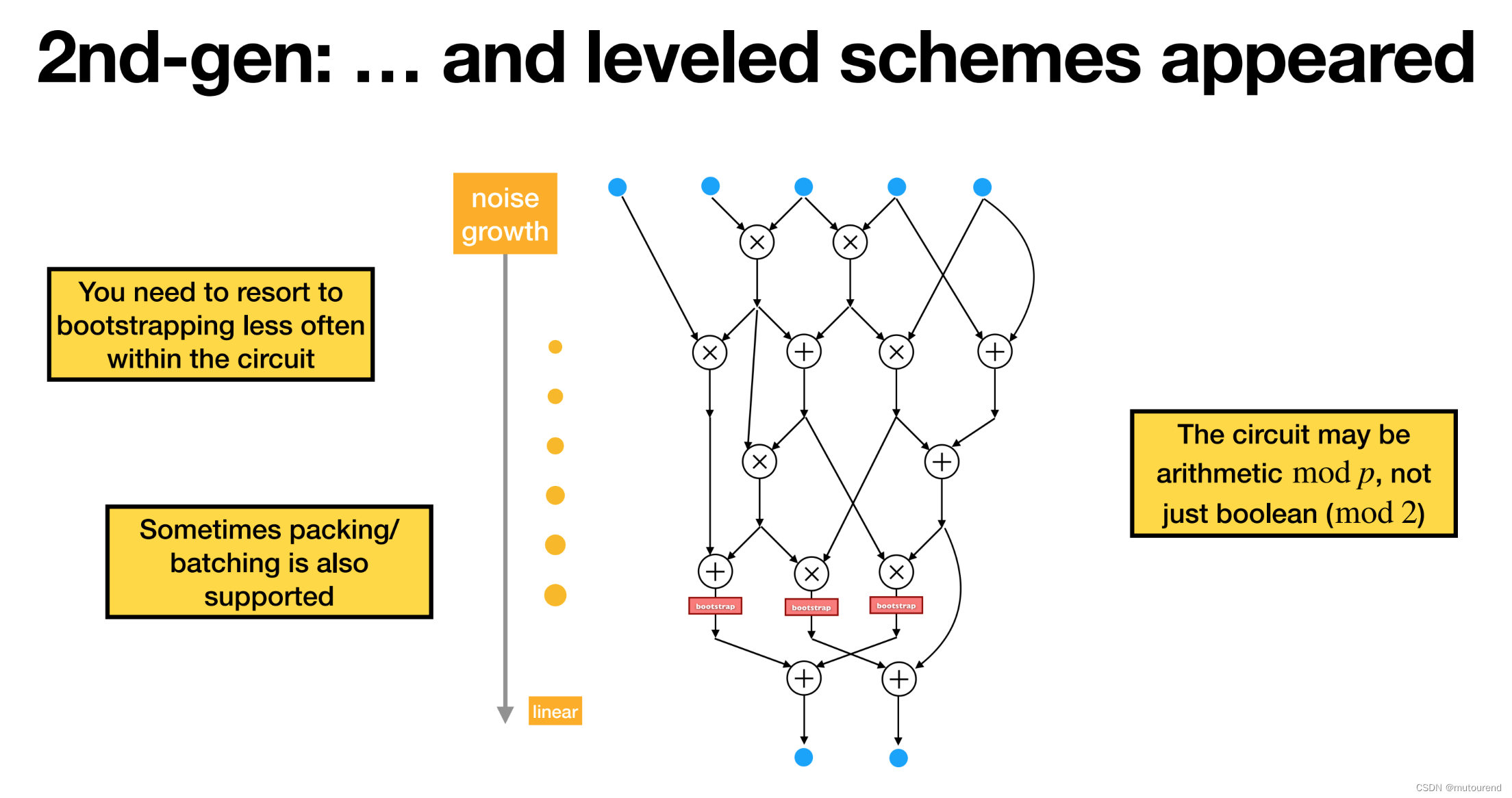
这即意味着,leveled schemes分支中的FHE方案:
- 其噪声是呈linear线性增长的。
- 相比于第一代FHE方案,电路内需要做bootstrapping的次数要更少。
- 有的第二代FHE方案中,引入了packing/batching概念——支持并行执行相同的boolean电路。
- 有的第二代FHE方案中,电路不再受限于boolean(即$\mod 2$),可为$\mod p$运算。
4. 第三代FHE
第三代FHE:代表作为2013年GSW、2014年FHEW(属fast bootstrapping分支)。
- 2013年GSW:做了概念简化,但基本上很慢。
- 2014年FHEW(属fast bootstrapping分支):对bootstrapping进行了大幅改进。
5. 第四代FHE
第四代FHE:代表作为2016年CKKS(属leveled schemes分支)、2016年TFHE(属fast bootstrapping分支)。
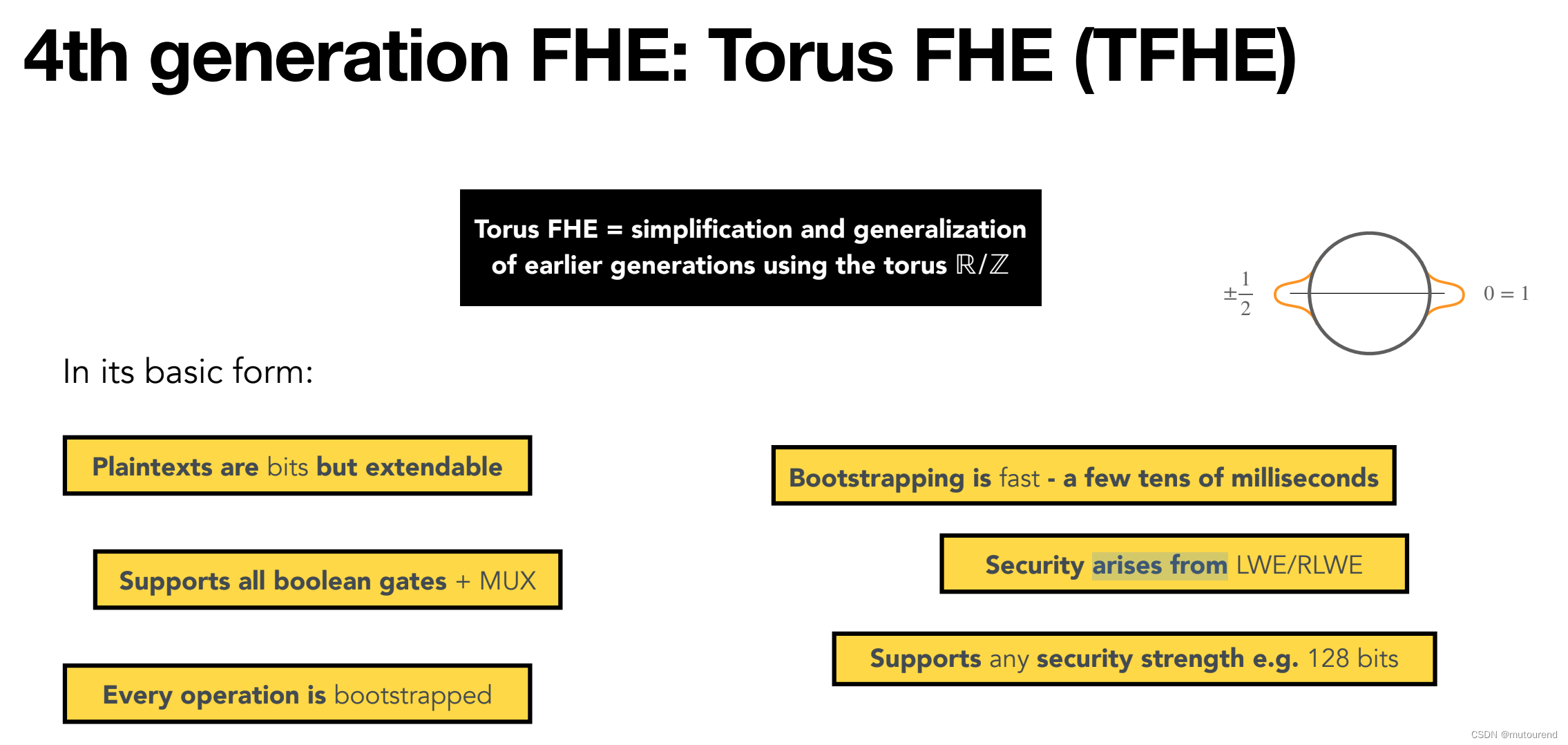
2016年TFHE(属fast bootstrapping分支):
- TFHE全称为Torus FHE
- 使用torus $\mathbb{R}/\mathbb{Z}$,对第三代的FHEW进行了简化和通用化。所谓torus,本质为real numbers modulo $1$——为$0$到$1$之间的实数集合。
TFHE基本格式为:
- 1)明文为bits,但可扩展(extendable)
- 2)支持所有boolean gates,以及,MUX gate。
- 3)每个操作都被bootstrapped
- 4)bootstrapping速度快,通常为几十毫秒。
- 5)安全性源自LWE(Learning With Errors)/RLWE(Ring Learning With Errors)。
- 6)支持任意安全强度,如128 bits。
参考资料
[1] Zama团队Pascal Paillier 2020年11月11日分享视频 001 Introduction to Homomorphic Encryption w/ Pascal Paillier(对应slide见:Introduction to Fully Homomorphic Encryption)
- 使用 Zama 构建加密 ICO 808 浏览
- 052:隐私计算:在公开账本中保护隐私 3069 浏览
- PSE 2025年10月周报 778 浏览
- 启动 Zama 开发者计划,以支持有兴趣使用 FHE 构建下一代区块链应用的开发者 1273 浏览
- 超越零知识:全同态加密如何实现私有共享状态 2005 浏览
- 全同态加密与真正隐私互联网的曙光 2685 浏览
- 宣布我们的 B 轮融资和 Zama 保密区块链协议 2173 浏览
- 什么是同态加密?- Chainlink 2973 浏览
- 使用全同态加密构建加密的 iOS 应用 1933 浏览
- Concrete v2.10:引入 Rust 支持并增强 TFHE-rs 互操作性 1837 浏览
- TFHE-rs v1.1:细粒度的 GPU 控制和更多算子 1455 浏览
- Concrete v2.10:引入 Rust 支持并改进 TFHE-rs 互操作性 3076 浏览

