EIP-2565: ModExp Gas 成本
| Authors | Kelly Olson (@ineffectualproperty), Sean Gulley (@sean-sn), Simon Peffers (@simonatsn), Justin Drake (@justindrake), Dankrad Feist (@dankrad) |
|---|---|
| Created | 2020-03-20 |
| Requires | EIP-198 |
Table of Contents
简单总结
定义 ModExp (0x00..05) 预编译的 gas 成本。
摘要
为了准确反映 ModExp 预编译的实际操作成本,本 EIP 规定了一种用于计算 gas 成本的算法。该算法近似计算乘法复杂度的成本,并将其乘以执行求幂所需的迭代次数的近似值。
动机
模幂运算是许多密码学函数(包括签名、VDF、SNARK、累加器等)的基础算术运算。不幸的是,ModExp 预编译目前的定价过高,导致这些操作效率低下且成本高昂。通过降低此预编译的成本,这些密码学函数将变得更加实用,从而提高安全性、更强的随机性 (VDF) 等。
规范
从 FORK_BLOCK_NUMBER 开始,调用地址 0x0000000000000000000000000000000000000005 的预编译的 gas 成本将按如下方式计算:
def calculate_multiplication_complexity(base_length, modulus_length):
max_length = max(base_length, modulus_length)
words = math.ceil(max_length / 8)
return words**2
def calculate_iteration_count(exponent_length, exponent):
iteration_count = 0
if exponent_length <= 32 and exponent == 0: iteration_count = 0
elif exponent_length <= 32: iteration_count = exponent.bit_length() - 1
elif exponent_length > 32: iteration_count = (8 * (exponent_length - 32)) + ((exponent & (2**256 - 1)).bit_length() - 1)
return max(iteration_count, 1)
def calculate_gas_cost(base_length, modulus_length, exponent_length, exponent):
multiplication_complexity = calculate_multiplication_complexity(base_length, modulus_length)
iteration_count = calculate_iteration_count(exponent_length, exponent)
return max(200, math.floor(multiplication_complexity * iteration_count / 3))
理由
在对 ModExp 预编译进行基准测试后,我们发现相对于其他预编译,它的“定价过高”。我们还发现,当前的 gas 定价公式可以改进,以更好地估计各种 ModExp 输入变量的计算复杂度。以下更改提高了 ModExp 定价的准确性:
1. 修改“计算复杂度”公式以更好地反映计算复杂度
EIP-198 中定义的复杂度函数如下:
def mult_complexity(x):
if x <= 64: return x ** 2
elif x <= 1024: return x ** 2 // 4 + 96 * x - 3072
else: return x ** 2 // 16 + 480 * x - 199680
其中 x 是 max(length_of_MODULUS, length_of_BASE)
EIP-198 中的复杂度公式旨在近似 Karatsuba 乘法的难度。但是,我们发现了一个更好的近似值来对模块化求幂进行建模。在本 EIP 中定义的复杂度公式中,x 除以 8,以计算多精度算术中的肢数。下面是当前“复杂度”函数与建议函数相对于执行时间的比较:
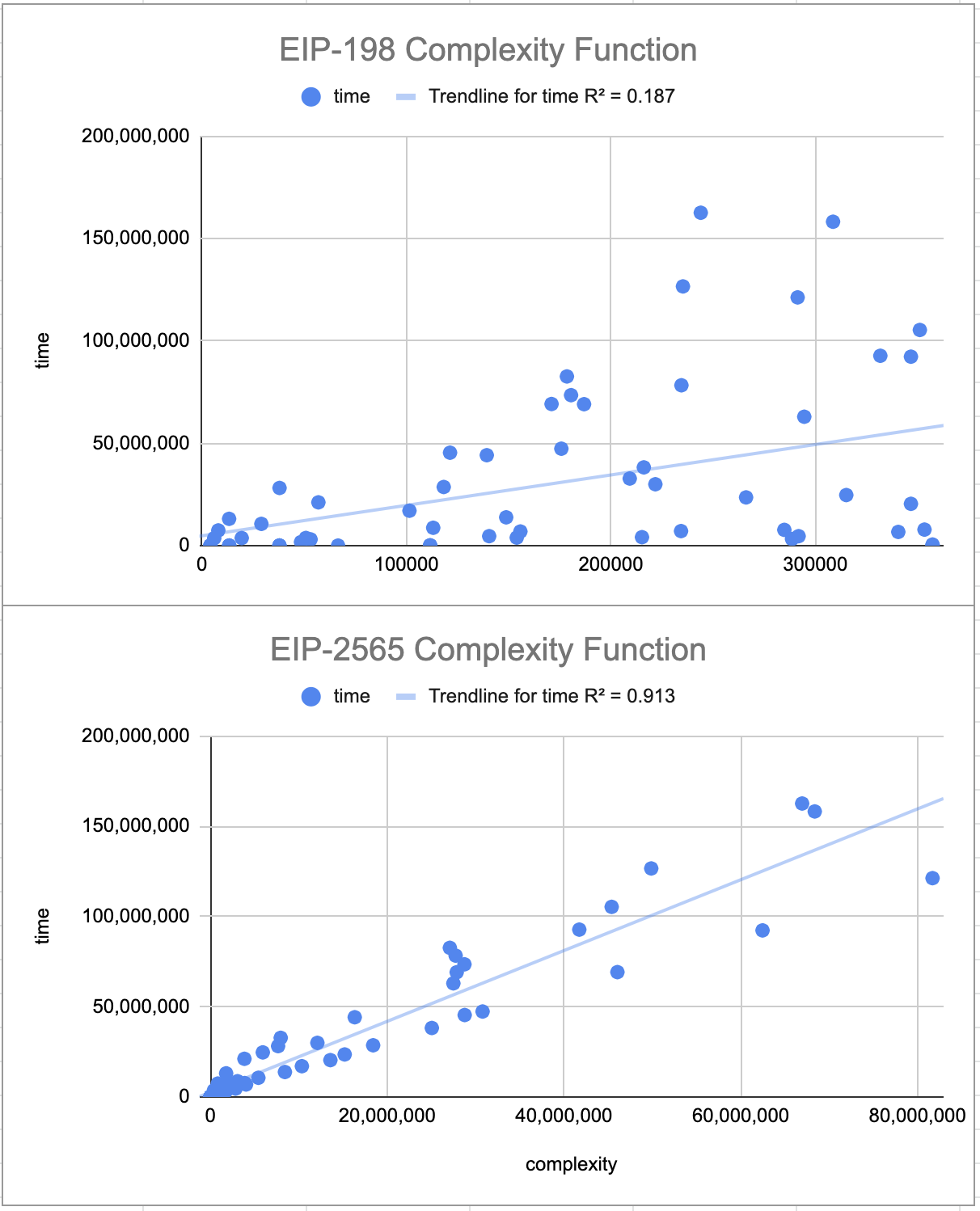
与 EIP-198 复杂度函数相比,此处定义的复杂度函数与执行时间具有更好的拟合度。这种更好的拟合是因为该复杂度公式考虑了“bigint”库用于大指数的二进制求幂算法的使用。您可能还会注意到建议的复杂度函数的回归线平分了测试向量数据点。这是因为运行时间因模数是偶数还是奇数而异。
2. 更改 GQUADDIVISOR 的值
在将 EIP-198 中的“计算复杂度”公式更改为此处定义的公式后,有必要更改 QGUADDIVSOR 以使 gas 成本与其运行时间一致。通过将 QGUADDIVSOR 设置为 3,ModExp 预编译的成本将高于(gas/秒)其他预编译,例如 ECRecover。
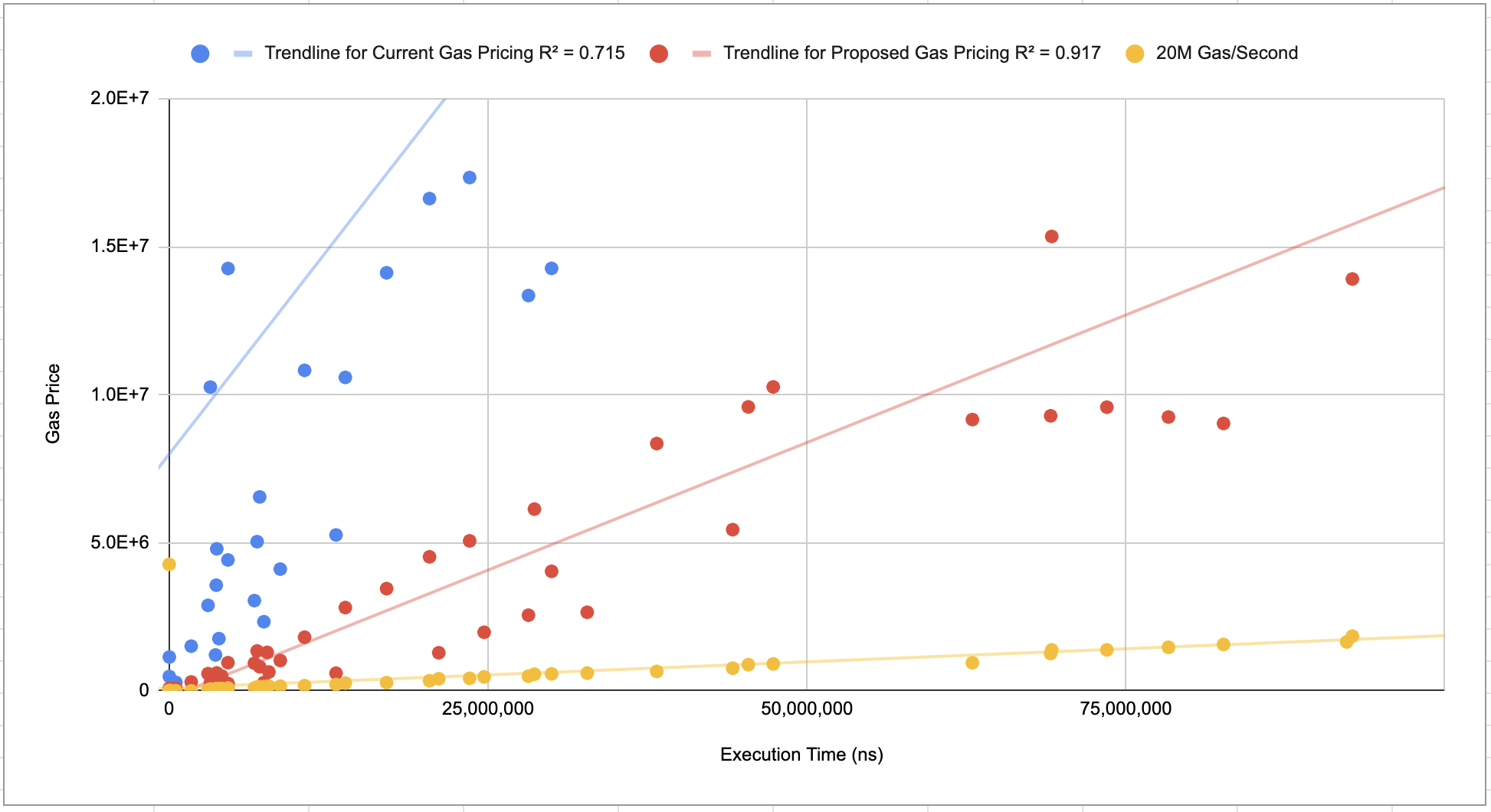
3. 设置最低 gas 成本以防止滥用
这可以防止预编译低估小输入值。
测试用例
底层接口或算术算法没有任何变化,因此可以重复使用现有的测试向量。下表包含更新后的测试向量:
| 测试用例 | EIP-198 定价 | EIP-2565 定价 |
|---|---|---|
| modexp_nagydani_1_square | 204 | 200 |
| modexp_nagydani_1_qube | 204 | 200 |
| modexp_nagydani_1_pow0x10001 | 3276 | 341 |
| modexp_nagydani_2_square | 665 | 200 |
| modexp_nagydani_2_qube | 665 | 200 |
| modexp_nagydani_2_pow0x10001 | 10649 | 1365 |
| modexp_nagydani_3_square | 1894 | 341 |
| modexp_nagydani_3_qube | 1894 | 341 |
| modexp_nagydani_3_pow0x10001 | 30310 | 5461 |
| modexp_nagydani_4_square | 5580 | 1365 |
| modexp_nagydani_4_qube | 5580 | 1365 |
| modexp_nagydani_4_pow0x10001 | 89292 | 21845 |
| modexp_nagydani_5_square | 17868 | 5461 |
| modexp_nagydani_5_qube | 17868 | 5461 |
| modexp_nagydani_5_pow0x10001 | 285900 | 87381 |
实现
安全考虑
此 EIP 的最大安全考虑因素是通过使 ModExp 操作相对于其计算时间而言过于便宜来创建潜在的 DoS 向量。
参考
版权
通过 CC0 放弃版权及相关权利。
Citation
Please cite this document as:
Kelly Olson (@ineffectualproperty), Sean Gulley (@sean-sn), Simon Peffers (@simonatsn), Justin Drake (@justindrake), Dankrad Feist (@dankrad), "EIP-2565: ModExp Gas 成本," Ethereum Improvement Proposals, no. 2565, March 2020. [Online serial]. Available: https://eips.ethereum.org/EIPS/eip-2565.