区块链上的随机性(一)概述与构造
- PRIEWIENV
- 发布于 2019-01-26 20:47
- 阅读 15303
本篇文章总结了目前主要的应用在区块链的不可预测随机数获取协议,并提炼出它们的设计思想,方法论以及依赖的假设,然后对他们进行比较。 本文分为两部分:第一部分介绍基本概念,并从零开始构造适用于分布式系统的随机数协议核心;第二部分介绍目前主流的应用在区块链项目中的随机数协议,并分析他们是如何使用第一部分所介绍的某类或者某几类协议核心。
本篇文章总结了目前主要的应用在区块链的不可预测随机数获取协议,并提炼出它们的设计思想,方法论以及依赖的假设,然后对他们进行比较。 本文分为两部分:第一部分介绍基本概念,并从零开始构造适用于分布式系统的随机数协议核心;第二部分介绍目前主流的应用在区块链项目中的随机数协议,并分析他们是如何使用第一部分所介绍的某类或者某几类协议核心。
本文假设读者已经具有基本的区块链知识,并对以太坊智能合约的基本原理和比特币共识协议的基本原理有大致的了解。
随机性 (Randomness) 的获取是区块链中很重要并且比较困难的一个课题。这里的随机性的获取包括但不仅限于:如何在智能合约中引入不可预测的随机数;如何在共识协议中安全地进行随机抽签。显然,上述对于随机性获取的问题描述已经说明了为何这个课题十分重要。而它的困难之处一方面来自于区块链系统的透明性——从通常意义上来讲,该特性会使得一切算法的输入,输出以及算法本身暴露给所有的系统参与者——因此,在密码学中广泛使用的伪随机数发生器不可以被直接以硬编码的方式或者是智能合约代码的方式应用在区块链系统中来获取安全的随机数。另一方面,随机数获取协议作为区块链系统的一个子协议常常与该系统下的其他协议有着强耦合的特性——例如,共识协议——也就是说,其他协议很有可能会影响随机数获取协议的安全性。这会使得随机数获取协议的设计变得非常复杂,常常需要具体问题具体分析。
随机性的定义
在日常生活中,我们经常会听到诸如“随机选择”,“伪随机数”,“随机模型”,“随机序列”之类的词汇,以及“伪随机数”、“真随机数”这样的概念。想要理解这些词汇和概念,必须要搞清楚随机是什么。事实上,与随机相对的是确定,因此,我们可以将随机直观上理解为不确定——无论是随机数,还是随机选择,我们都希望这个数或者选择的结果从某种程度上来讲是不确定的。因此,如果直接给出一个数,而不给出这个数的产生方式,它不能被称之为随机数,比如直接给出一个数字 1,我们不能说 1 是随机数,但是如果这个 1 是通过掷骰子决定的,则可以说这个 1 是随机的。当然,这些都是非常直观而宽泛的理解。更精确地讲,“随机”,或者我们说“随机数”、“随机序列”,在不同的领域有不同的定义。在数学上,随机数的定义和概率论相关,计算复杂性理论使用描述随机序列的程序长度来定义,密码学会结合统计特性和密码攻击来描述随机数。我们这里先给出随机序列的描述性定义:
我们可以称一个序列为随机序列,当它满足:
- 均匀性:该序列服从均匀分布。
- 独立性:该序列的各个元素相互独立。
- 不可预测性:依据该序列的任意片段,不能预测该序列余下的部分。
展开来讲,我们可以先考虑如下问题:
-
考虑一个每一项要么取 1 要么取 0 的数列。假设它的每一项均为1,它显然不是随机序列,因为违反了均匀性。均匀性要求0和1出现的概率相同。
-
假设它的每一项都和前一项不相等。比如 “0101010101”,它满足了均匀性,但是仍然不是随机序列,因为违反了独立性。
-
对于一个满足独立性和均匀性的随机序列。比如从常数 $e$ 的小数点后第 10 位开始依次选取数码组成序列。这样的序列在统计上满足独立性和均匀性,但是它的序列是可以被预测的。
我们说过,不同的领域对随机性有不同的定义。比如,在仿真当中我们想要模拟顾客到达的间隔时间,用只满足前两条的随机序列是足够的。但是在密码学中,比如生成随机的密钥,仅满足前两条的随机序列是不够的,一个有可能被预测的随机序列用在密钥生成中当然是有安全问题的。比如我们用自然对数的底 $e$ 的数码作为随机序列。 $e$ 确实可以被认为在统计上是均匀分布和独立的(尽管没有完全证明),用来做仿真是足够的,但是不能用作密码学中的随机种子。因为对手有可能通过一定长度的已知序列猜测到是在使用 $e$ 。 另外,在抽奖,游戏当中使用的随机数也通常是要求不可预测的。鉴于区块链领域中涉及的多是密码学和游戏的场景,接下来的内容都是满足全部三条性质的随机序列。
随机序列又可以被分为真随机 (True Random) 序列和伪随机 (Pseudorandom) 序列。 伪随机序列,顾名思义,就是“不是真的随机,只是看起来是随机的”。因此,根据图灵奖得主姚期智先生 [1] 提出的概念,粗略地讲,伪随机序列就是指一个与真随机序列在计算上不可区分的序列。 而真随机序列,粗略地讲,指的是不可被重现的随机序列,比如通过抛硬币产生的随机序列。我们可以看出来,在这样的定义下,伪随机序列的统计特性应当和真随机序列无法区分,也就是说,伪随机序列同样是满足全部三条性质的随机序列。当然,这样的定义通常用在计算复杂性理论以及密码学当中,在其他领域,只满足前两条性质的随机序列也可以被称作伪随机序列。
产生随机序列的发生器叫做随机数发生器 (Random Number Generator, RNG) 。按照产生的序列的性质,我们可以将其分为真随机数发生器 (True Random Number Generator, TRNG) 和伪随机数发生器 (Pseudorandom Number Generator, PRNG)。此外,还有一种与之正交的分类方法是从随机数发生器的实现方法来分类,可以将随机数发生器分为硬件随机数发生器和软件随机数发生器,它们之间的关系如 下图1 所示
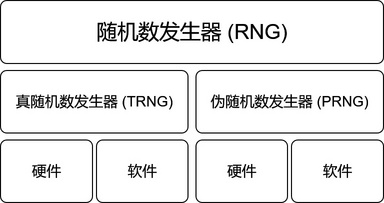
图1:随机数发生器的分类
真随机数发生器通常利用一些非确定现象,通过物理手段将其转换为真随机序列。通常的非确定现象包括混沌效应和量子随机过程。其中混沌效应的特点是目前物理学能够明确解释其因果,但是由于结果对于初始值过于敏感,导致无法精确预测其结果。比如,通过收集大气噪声而产生的随机数。而量子随机过程则是利用微观量子态的不确定性,这个不确定性已经被目前物理学理论承认,它能够保证即使输入值完全相同,输出值也是可能完全不同的。比如利用激光器的相位噪声来生成随机数。硬件真随机数发生器,通常使用芯片实现;而软件真随机数发生器,通常利用系统自带的一些非确定现象,譬如硬盘寻道时间、RAM 中的内容或者是用户的输入,Linux 系统里的/dev/random就是一种软件真随机数发生器,它通过采集机器运行过程中的硬件噪音数据来获取足够的随机性来源,并依此生成随机数。
伪随机数发生器是一段程序,是一种确定性的算法,通常以短的真随机数作为输入,进行扩充,生成更长的和真随机序列非常接近的随机数序列。它的输入被称作种子 (Seed)。它同样也有硬件实现和软件实现。
如何从区块链上取得随机数
上一节中我们给出了随机性的一个定义,这样的定义也将用于本文余下的部分。并且,我们还给出了伪随机性以及伪随机数发生器的概念。在实际应用中,可用于密码学的伪随机数发生器有很多并且也已经很成熟了,那么我们很自然地想到,能否将伪随机数发生器用于区块链,在区块链的共识过程或者应用上面加入随机性,使得这样的随机性满足我们上面提到的三条性质?显然,答案是否定的。伪随机数发生器产生的随机序列的不可预测性的前提是伪随机数发生器作为一个黑盒,除了它的输出,外界无法得知其他一切信息。但是区块链上的一切都是公开透明的,包括使用的伪随机数发生器及输入到伪随机数发生器里面的种子也是一样公开透明的。在这样的情况下,所有传统的伪随机数发生器都无法在区块链的环境下产出具有不可预测性的随机数序列。而至于真随机数发生器,是存在将真随机数发生器的结果通过可验证的不可篡改的通道,引入区块链系统内部,这样的通道又被称作 Oracle。以太坊现在常用的随机数发生器就是通过 Oracle,引入 random.org(random.org 是一个网站,它声称提供真随机数)提供的随机数。这种方法的问题在于,所谓的“真随机数发生器”往往是中心化的,拥有这样的硬件或者软件的人或者组织拥有篡改随机数发生器结果并不让用户发觉的能力。这对于主打去中心化的区块链系统来说,无疑是如鲠在喉。
除了伪随机数发生器和真随机数发生器,还有一类直接利用区块链系统中共识过程所天然产生的随机性。比如,使用未来某个块或者之前某个块的 Hash 值来作为种子之一生成随机数(其他的种子可以是用户的地址、用户支付的以太币数量等,但是这些是用户可控的部分,没有增加不可预测性的作用)。这种做法也常见于各种区块链博彩类游戏以及资金盘游戏当中,但是这样的随机数获取过程有着致命的漏洞——用户有可能通过仔细选择交易时间来控制随机数向有利于自己的方向生成;即使用户无法控制,矿工也可以控制随机数的生成,并且这样的攻击成立并不需要太多算力的参与。只要最终随机数牵涉的金额足够,完全可以使用租用算力或者贿赂矿工的方式进行攻击。
那么归根结底,在区块链这样的一个系统当中随机性可以来自哪里呢?也就是说,通过上面的分析,我们发现,无论规则或者程序设计得如何复杂,它都是确定性的算法。对于一个确定性的算法,算法本身不会对输出的随机性有任何的影响,能够影响最终输出的随机性的,只有算法的输入。因此,在区块链系统当中,我们需要在一个分布式的,公开透明的环境中去仔细选择一个有足够随机性的输入。这样的输入实际上来源于我们对于区块链系统参与者之间不是一个整体的假设。
随机数生成协议模型
我们现在从最简单的情况开始去逐步构造一个区块链上可以使用的公平的随机数发生器。下文所涉及到的在分布式的环境下的协议都可以转换为区块链的环境,因此不对“分布式”和“区块链”做区分。
“分布式”和“区块链”的区别
区块链系统属于分布式系统,但是分布式系统不仅仅是区块链系统,还包括点对点文件传输系统,分布式数据库系统等等。“分布式”只是对网络的拓扑结构进行描述,表明网络不是集中式的,而是分布的多节点控制的。
为了更清楚地说明构造分布式随机数协议,也叫分布式随机数信标 (Distributed Randomness Beacon, DRB),的方法论,我们首先引入一个随机数协议的抽象模型:
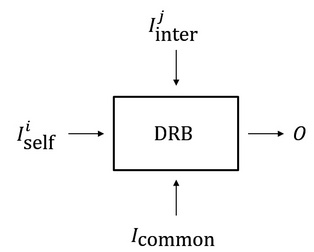
图2: 随机数协议的抽象模型
这个模型能够完整地描述一个分布式随机数协议的输入输出与其节点之间的关系。如上图2所示,假设每个节点地位相同,不做区分,那么每个节点都会运行同样的协议。一个分布式随机数协议包含三部分的输入:每个节点 $i$ 自己的输入 $I{self}^i$ ,来自其他节点的输入 $I{inter}^i$ ,$j≠i$ 以及一个公开的预先约定好的公共输入 $I{common}$,这三部分输入每一部分都可以包含多次的输入。作为一个分布式随机协议,其输出随机性的来源只能由输入提供,我们先不考虑这三部分输入进入协议的先后顺序,那么我们可以将协议分为两类,一类是采用 $I{self}$ 与 $I{inter}$ 作为随机性来源的协议,另一类是采用 $I{common}$ 作为随机性来源的协议,大家可以发现,这两类事实上已经涵盖了所有的随机性来源的可能,其他类别的协议都可以视为这两类协议的组合。文章后面的部分将主要对这两类协议展开分析。
采用 $I{self}$ 与 $I{inter}$ 作为随机性来源
下面,我们考虑这样的一个场景:Alice 和 Bob 在网上凑钱一起买了一张彩票,结果中了神秘的头奖,令他们吃惊的是,奖金竟然是一只他最喜欢的卡通皮卡丘,如下图 3 所示。但是奖品不可分割,并且由于两人相隔甚远无法见面猜拳,所以他们俩决定设计一个对两个人都公平的随机数生成协议来确定谁能获得这份奖品。

图3: 动漫奖品
v1.0:最简单的随机数生成协议
Alice 设计了如下图 4 所示的一个协议,这个协议又被称作(抛硬币协议) Coin-Tossing Protocol 或是 Coin-Flipping Protocol。协议接收每位参与者的一次输入,在该场景下是 $ ξA $ 和 $ξB$,输入的取值只能是 0 或者 1。协议拥有唯一公共输出 $ξ$,取值也是 0 或者 1,如果最后 $ξ =0$,Alice 获得奖品;若 $ξ=1$, Bob 获得奖品。而从每一位参与者的角度来讲,这个协议接收自己的输入以及其他运行这个协议的节点的输入,经过算法运算之后,输出一个一致的最终结果,其实就是上一节中我们提到的抽象模型中的,利用 $I{self}$ 与 $I{inter}$ 作为随机性来源的协议。

图 4:抛硬币协议 Coin-Flipping 或 Coin-Tossing 协议
那么这样的协议具体是怎么做的呢?为了构造这样的一个协议,我们需要确定这样的协议需要满足什么样的性质。考虑到每个人之间的输入是相互独立的,这样的协议需要保证每个人自己的输入也应当是和输出相互独立的,但是他们又共同对输出做出了一定贡献。只有这样,才能确保每个人都无法光凭借改变自己的选择来改变输出。同时,协议也需要保证只要有一个人的输入是均匀分布的,那么结果就是均匀分布的。现实中满足这些条件的构造方式有很多,其中一种是异或操作,将两人的输入异或之后输出:在给定 Bob 选 1 的情况下(Alice 不知道),Alice 不管选 0 还是 1,输出结果都是 0 和 1 各一半的可能性;给定 Bob 选 0 的情况同理。 $ξ=ξA⊕ξB$
另一种方法是利用 mod 加法,将两人的输入进行模 2 加法之后输出。 $ ξ = ξA + ξB\quad mod\ 2 $
v2.0:带有承诺的版本
v1.0 看似解决了我们的问题,实际上它有非常大的漏洞。这个漏洞在于,我们无法保证 Alice 和 Bob “同时” 输入。假如 Bob 等 Alice 向协议输入她的选择之后再进行选择,那么由于协议的交互对于两人来讲是公开的,Bob 可以根据 ALice 的选择来调整自己的选择。例如,如果 Alice 的选择是 0,那 Bob 就输入 0;如果 Alice 是 1,那他就输入 1。这样,无论 Alice 怎么选择,Bob 都可以使得异或的结果永远是 1,就能拿走这奖品。
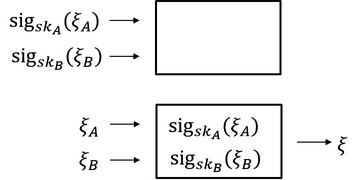
图 5:带有承诺的 抛硬币协议 Coin-Tossing
事实上,同时输入是很难保证的,而为了防止这种作弊行为,我们需要保证,协议的来自其他人的输入对于参与者来讲应该是暂时机密的,不会透露任何他们的选择的信息。与此相应的,应该多出一个去机密化的过程以计算出协议的输出。为了实现这样的需求,我们需要引入新的机制:承诺 (Commitment)。如上图 5 所示,该机制包含两个阶段:承诺 (Commit) 阶段和揭示 (Reveal) 阶段。 在第一个承诺阶段,协议参与者不再直接输入自己的选择,而是对自己的选择进行数字签名,将签名的结果,我们称之为承诺,输入进协议。例如,Alice 会将她的选择 $ ξA $ 用自己的私钥 $skA$ 进行签名,获得结果 $sig_{skA}(ξA )$ 输入进协议。 当所有参与者的签名结果均输入进协议中后,进入第二个揭示阶段。该阶段所有参与者将第一轮自己的选择输入进协议,例如 Alice 会输入 $ ξA $。协议会结合第一个阶段的承诺进行验证,如果所有的验证都通过,则输出最终结果 $ ξ $,最终结果就是我们想要的随机数。
这样的协议保证了,在第一个阶段里没有任何人的选择会被除自己以外的其他人获知,并且在第二阶段,即使 Bob 先知道了 Alice 揭示出来的选择值然后在自己揭示之前计算出结果,他也无法改变自己的选择了,因为第一个阶段的签名已经做出了“承诺”。这里,数字签名能够保证消息的不可篡改性,不可否认性以及暂时的机密性。如果该协议是运行于区块链之上,由于通常区块链协议都会对交易内容进行数字签名,那么我们的协议也可以将使用数字签名改为使用 Hash 函数。
v3.0a:使用经济惩罚
v2.0 的版本在对于两个人的情况的时候看起来非常公平,但是对于两人以上的情况,它仍然是有漏洞的。假设 Alice、Bob、Clare 三个人分奖品,其他设定不变,采用 v2.0 协议。这时,Bob 想到了个主意:“在最后的第二阶段,我可以在输入自己的选择进行揭示之前先依据别人的揭示结果计算出输出,如果不是对我有利的输出,我就不进行揭示阶段,假装网线被挖断了。”
刚才的协议无法处理这种情况。是重新再来一遍,还是就取剩下两个人的输入呢?这两种方法是都有问题的:如果重新再运行一遍协议,那么攻击者就可以利用这种重新运行的机制在每次自己不利的情况下强行使得协议重新运行;如果只取剩下两个人的输入,攻击者同样可以利用这种机制选择是否放弃输入来趋利避害。因此,我们需要有一种机制来保证参与者不得随意放弃,最简单的方式就是利用经济惩罚。如下图 6 所示,当参与者在第一阶段承诺的时候,必须要向协议锁定一个比特币(也可以是其他的数字货币)——如果是在带有智能合约的区块链的环境,这样的操作十分容易。如果 Bob 不按时揭示他的选择 $ ξB $ ,那么就会没收 Bob 的比特币分给 Alice 和 Clare,然后重启协议。由于奖品的价值(也许)通常并不会超过一个比特币,Bob 不会选择这样的方式进行作弊。这样的一个惩罚机制,就是为了防止这样的拒绝服务攻击。
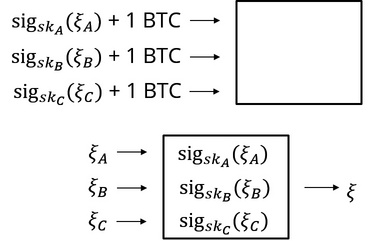
图 6:带有经济惩罚的版本
需要注意的是,之所以本节一开始所述的攻击对只有两个参与者的协议不奏效,是因为两个人的情况下,在仅剩一个人的时候,我们可以直接给出有利于剩下的参与者的结果,而在多于两个人的情形下,我们仍旧无法保证在剩下的人当中做出选择。这样的规则是一种天然的对拒绝服务的参与者的惩罚。
v3.0b:使用门限机制
除了经济惩罚之外,还有另外一种方式,我们称之为门限 (Threshold) 机制。门限机制指的是一种协议的某一个指标达到一定阈值就可以执行特定流程的机制。在这里我们引入门限机制,主要是为了使得在协议参与人数有缺失的时候仍然能够给出正常的输出。门限机制的作用在于增强协议的健壮性,使得它能够容忍一定程度的拒绝服务攻击。我们接下来讨论的门限机制都是 $(t,n)$ 门限机制,意思就是对于 $n$ 个参与者的协议,只需要 $t$ 个参与者的输入即可完成协议的输出,注意这里的 $n$ 不一定是协议预先规定好的,或者说是协议必须知道的,它也有可能是一个不确定的数字。如果协议必须规定了确切的 $n$ 才能够保证正确性,那么这样的协议只能用于许可环境 (Permissioned Setting) 中;如果不需要规定确切的 $n$,那么这样的协议可以被用于非许可环境 (Permissionless Setting) 中。如图 7 和 图 8 所示,我们使用最基本的 v1.0 版本的 Coin-Tossing 协议,将门限机制的输出作为 Coin-Tossing 协议的输入。这样的门限机制总的说来有三种。

图 7:Coin Tossing 抛硬币协议
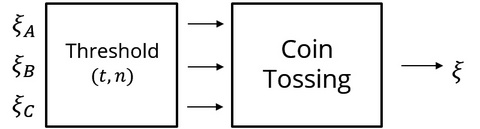
图 8:带门限机制的 Coin Tossing 抛硬币协议
第一种门限机制是将输入按照某种规则排序之后,简单地取前 $t$ 个输入。但是这种方式不抗女巫攻击 (Sybil Attack)——假如 Bob 是黑客帝国的复制人,他复制了一万个自己,因此 Bob 通过控制这一万个身份有很大的可能占有前 $t$ 个输入,从而控制随机数的结果。因此,这种门限机制是无法用在没有抗女巫攻击机制的环境下——譬如,没有身份验证的非许可环境下。它的优点在于,这样的机制不需要知道 $n$ 的确切值。
女巫攻击 简单来讲,指的是一种网络内的少数节点控制多重身份以消除冗余备份的作用的攻击方式
第二种门限机制是无分发者的秘密分享系列的。秘密分享可以将一个秘密分成多个碎片,只有集齐一定数量的碎片才能将秘密恢复出来。通常,秘密分享需要有一个可信第三方充当分发者将秘密分成秘密碎片然后分发。而无分发者的含义则是秘密分享的过程不需要这样的分发者,也就是说,更加去中心化了。它一般有三种不同的形式:第一种是无分发者的秘密分享 (Secret Sharing);另一种是无分发者的可验证秘密分享 (Verifiable Secret Sharing);最后一种是无分发者的公开可验证秘密分享 (Publicly Verifiable Secret Sharing)。当然,这三种方式是有区别的。第一种无法验证,秘密碎片可以被伪造。第二种的秘密碎片可被验证,但是验证不是每个人都可以做的,每个人只能验证自己的那一份碎片。最后一种是可被公开验证的,每个人都可以验证所有的秘密碎片。这三种方式均需要每产生一个随机数输出都进行一次秘密分享来保证门限机制,属于有状态 (Stateful) 协议。更直观地讲,比如有 $n$ 个人,假设只需要有 $t$ 个人提交了就能输出我们想要的随机数,同时,我们需要 $r$ 个这样的随机数。那么如果采用无分发者的秘密分享系列的门限机制,我们需要这 $n$ 个人相互交互至少 $r$ 轮。另一个局限是,该方案需要在许可环境下实施,也就是说协议必须知道总人数 $n$,才能确定合理的门限 $t$。
我们这里仅介绍第一种形式和第三种形式。如下图 9 所示,第一种形式——无分发者的秘密分享——首先要分发,比如说 Bob 把他的选择 $ ξB $ 分成三份:$s{ξB}^A$ ,$s{ξB}^B$, $s{ξB}^C$ ,这三份中的任意两份都可以恢复出完整的 $ ξB $ 。上角标代表了这个份额发送给的人,例如 $s{ξB}^C$ 表示该份额发送给 Clare。每个人都像 Bob 这样做之后,每个人手上都有 3 份来自包括自己在内的不同的人的份额。例如,Clare 此时手上应该有 :$s{ξA}^C$ ,$s{ξB}^C$,$s_{ξC}^C$ 。此时,每个人再把这些份额拼成份额向量广播给所有人。例如 Clare 会将份额向量
$s^C = [s{ξA}^C ,s{ξB}^C,s_{ξC}^C]$
广播给其他两个人。这样每个人只要手里有包括自己在内的两份这样的向量就能恢复出 Alice、Bob 和 Clare 三人的选择,然后就可以算出最终的随机数,例如 Bob 拥有向量
$s^B = [s{ξA}^B ,s{ξB}^B,s{ξC}^B]$ 和 $s^C = [s{ξA}^C ,s{ξB}^C,s{ξC}^C]$
下角标相同上角标不同的任意两个份额都可以恢复出相应的秘密,例如 $s{ξB}^B$ 和 $s{ξB}^C$ 可以恢复出$ξB$。由于这一点,我们可以得到 $[ξA,ξB,ξC]$,由此算出最终的结果 $ξ$。
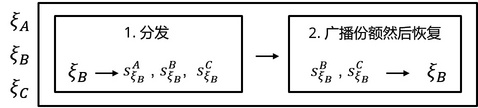
图 9:无分发者的秘密分享
但是这样的秘密分享方案是有漏洞的,如果秘密分发者——譬如 Bob——在分发份额 $s{ξB}^A$ ,$s{ξB}^B$ ,$s{ξB}^C$的时候,将其中一份份额 $s{ξB}^A$ 替换为其他的一个任意值,那么收到这个份额的 Alice 在使用该份额进行恢复的时候有可能恢复出错误的 $ ξB $。为了防止这样的攻击,我们需要可验证的秘密分享方案。
如图 10 所示,第三种形式——无分发者的公开可验证秘密分享——与第一种相比则是在分发阶段的时候多了一些额外的数据。这些数据就是“证明”,记作
$π$。“证明” $π$ 可以被用来检验每个人收到的份额是否和其他人的一致。所有人都会使用这个公开的 $π$ 去验证收到的份额,验证通过就可以说明这个份额确实是和其他发出去的份额是一致的,都是按照正确的规则生成的。

图 10:无分发者的公开可验证秘
第三种方法是分布式密钥生成 (Distributed Key Generation) + 门限签名 (Threshold Signature)。门限签名可以理解为秘密分享应用到了数字签名方案中,但是它又不是单纯将两者相叠加。通常的数字签名方案是,一个人用自己的私钥加密了消息获得签名之后,签名可以被公钥等公开参数验证。而该方案使用的门限签名方案里同样有一对公私钥,但是每个参与者分别只有总私钥的其中一个碎片以及相应的公钥碎片;这些私钥碎片集合起来可以恢复出完整的私钥,公钥碎片同理;每个人可以利用自己的私钥碎片进行签名获得签名碎片,这些签名碎片可以被公钥的相应碎片验证;并且,这些签名碎片中的任意 $t$ 个合起来可以计算出一个总签名,该总签名相当于用总私钥进行签名,因此也能被总公钥验证。故而这样的签名过程并不需要所有人参与,只需要 $n$ 个人中的 $t$ 个人的有效签名即可完成签名过程。而且无论是哪 $t$ 个人参与签名,最后生成的签名是一样的。并且签名过程中涉及到的私钥不会被泄露,每个人分享的只有公钥碎片和自己的签名结果,这使得多轮无交互签名成为可能。当然,这个总的公私钥对以及相应碎片不是任意选取的,它的生成需要所有的 $n$ 个人在协议第一次运行时运行分布式密钥生成协议才能生成有这样的密码学特性的公私钥对及其碎片。因此,这个方案同样存在协议必须要知道总人数 $n$ 的问题。
使用 $I_{common}$ 作为随机性来源
使用 $I{common}$ 作为随机性来源,最常见的方法是采用比特币链上未来某一个块的 Hash 值作为 $I{common}$ ,或者使用当日股票市场上某一支股票的收盘价。但是这个方法的问题在于,输出 $O$ 完全由 $I{common}$计算得来,攻击者有可能通过操纵 $I{common}$ 的值来使得 $O$ 变为他想要的值。如果从 $I{common}$ 计算$O$的过程没有那么容易,比如说有可能要耗上一整天,那么攻击者将没有足够的时间去提前预测$O$的值。为了实现这样的需求,我们引入了一个新的密码学工具:可验证延迟函数 (Verifiable Delay Function, VDF) (参考[2]) 。这样的工具能够使得输出$O$在给定时间 $t$ 内是很难通过输入 $I{common}$ 计算出的,即使拥有任意的并行处理器以及多项式级别的提前计算量。同时,输出 $O$ 是唯一的并且可以被公开验证是由 $I_{common}$ 正确计算得来的。它很像 PoW,但是 PoW 不抗并行处理器及多项式级别的提前计算攻击,也就是说,使用并行处理器能够显著缩小 PoW 的计算时间到远远小于 $t$。使用 VDF 可以保证在给定时间内全世界没有任何一个人可以预测与给定输入相匹配的输出。以太坊 2.0 已经计划使用 VDF 作为随机数信标。
参考文献
[1] Yao, Andrew C. “Theory and application of trapdoor functions.” Foundations of Computer Science, 1982. SFCS’08. 23rd Annual Symposium on. IEEE, 1982.
[2] Boneh, Dan, et al. “Verifiable delay functions.” Annual International Cryptology Conference. Springer, Cham, 2018.
本文依照 BY-NC-SA 许可协议转载,原文链接。
学习中如遇问题,欢迎到区块链技术问答提问,这里有专家为你解惑。 深入浅出区块链 - 高质量的区块链技术博客+问答社区,为区块链学习双重助力
- PREVRANDAO 取代 DIFFICULTY 操作码 13 浏览
- Solidity 弱随机数的不安全性 1503 浏览
- Chainlink VRF 深度解析与实战 4785 浏览
- Solidity 安全注意事项 1964 浏览
- 以太坊提案者选择机制在 Electra 更新前后的变化 1779 浏览
- 使用 Aptos Move 实现随机数生成:从 AIP-41 到实战操作 3425 浏览
- 区块链 - Pyth的Entropy - Pineanalytics 1235 浏览
- NFT游戏是什么?简单解释 1398 浏览
- 为什么真随机性在Web3中很重要 1584 浏览
- 研究如何利用 Solidity 新操作码 Prevrandao 获取随机数 7372 浏览
- 在区块链上使用Solidity生成一个随机数 2112 浏览
- 该怎么猜智能合约上的随机数? 4832 浏览

