Mina Learning - Polynomial commitment
- longerd
- 发布于 2024-12-03 15:34
- 阅读 2104
介绍常见的多项式承诺
多项式承诺是一种方案, 它允许你对一个多项式(即对其系数)做出承诺. 之后, 有人可以要求你在某个点上对多项式进行求值并给出结果, 你可以做到这一点, 同时还能提供正确求值的证明.
承诺应具有 hiding 和 binding 属性. 同时具有一定的同态属性(如基于 pairing 的承诺具有乘法同态属性; 基于 DLG 的承诺具有加法同态属性).
Binding: 不存在 $m' \not = m$, 使得 $\text{Commit}(m, r) = \text{Commit}(m', r')$.
Hiding: 对于随机数集合 $\mathbb{R}$, $\text{Commit}(m, \mathbb{R}) \equiv \text{Commit}(m', \mathbb{R})$. 即承诺 $\text{Commit}(m, r)$ 也不会泄露 $m$ 的任何信息.
多项式承诺中包含的3个主要算法为:
- Commit
- Open
- Verify
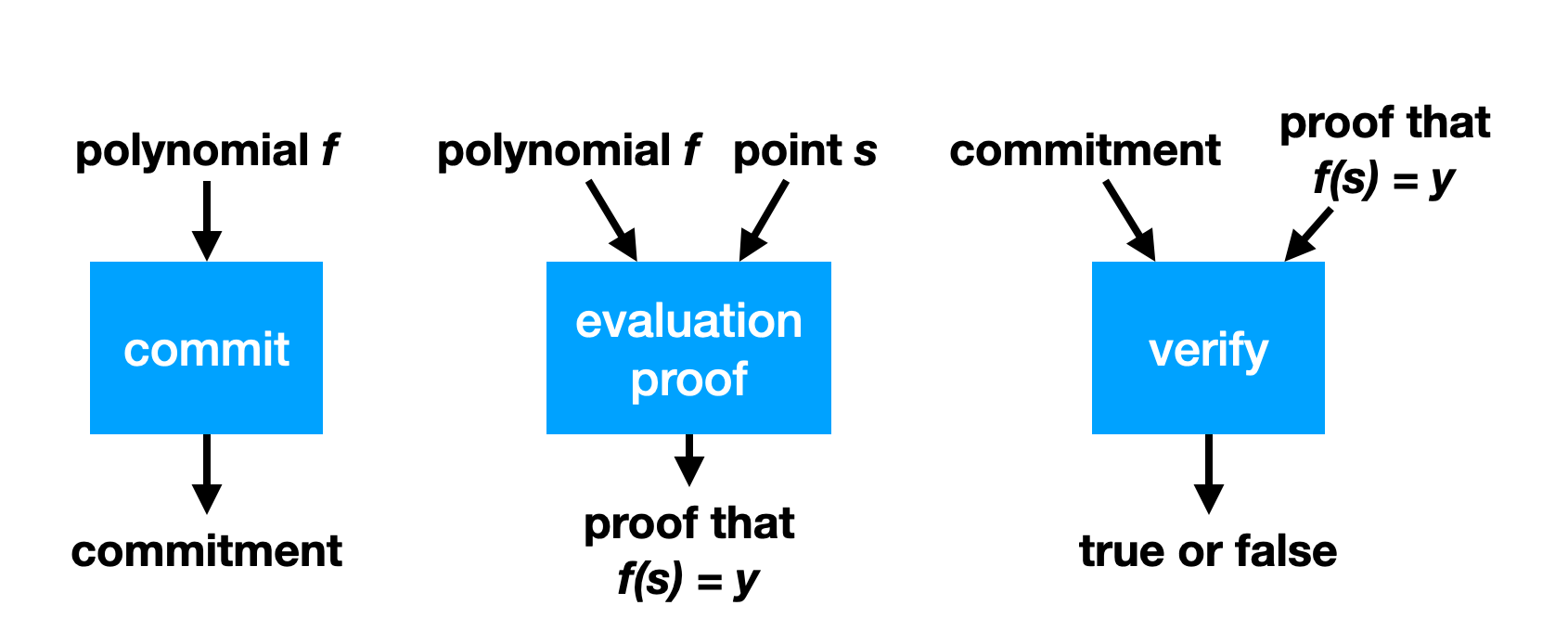
Pedersen hashing and commitments
简单的非隐藏承诺: Pedersen hash. 要对单个值 $x$ 进行承诺, 只需计算 $xG$, 其中 $G$ 的离散对数是未知的. 要打开承诺, 只需揭示值 x.
使用 Pedersen hash 可以进行多重承诺. 对于一个值的向量 $(x{1}, \cdots, x{k})$, 可以通过计算 $x{1}G{1} + \cdots + x{k}G{k}$ 来实现多重承诺. 其中每个 $G{i}$ 都是不同的, 并且也具有未知的离散对数. 通常会将最后这个公式简化表示为内积 $<\vec{x}, \vec{G}>$, 这里 $\vec{x} = (x{1}, \cdots, x{k})$, $\vec{G} = (G{1}, \cdots, G{k})$. 要揭示这个承诺, 只需揭示出值 $x{i}$.
Pedersen hash 承诺是非隐藏但具有绑定性的, 因为你不能将它们打开为与最初承诺不同的值. 同时将 $x$ 和 $y$ 的承诺相加会得到 $x + y$ 的承诺: $xG + yG = (x + y)G$, 这在我们的 IPA 协议中会很有用.
Inner product argument
给定域 $F$ 上的两个长度为 $n$ 的向量, 证明它们的内积 $< \vec{a}, \vec{b}> = z$.
对于多项式 $f$ 的系数向量 $\vec{f}={a{0}, \cdots, a{n}}$, 有 $f(x) = a{0} + a{1}x + \cdots + a_{n}x^{n}$.
注意 $f(s) = <\vec{f}, (1, s, \cdots, s^{n})> $即是内积表示.
Setup
仅证明者知道的秘密向量是 $\vec{a} = (a_1,a_2,a_3,a_4)$.
所有参与者都知道的有:
- $\vec{G} = (G_1, G_2, G_3, G_4)$, Pedersen hash 的一个基
- $A = \langle \vec{a}, \vec{G} \rangle$, $\vec{a}$ 的承诺
- $\vec{b} = (b_1, b_2, b_3, b_4)$, 某个值 $s$ 的幂, 使得$\vec{b} = (1, s, s^2, s^3)$
- 内积的结果 $z = \langle \vec{a}, \vec{b} \rangle$
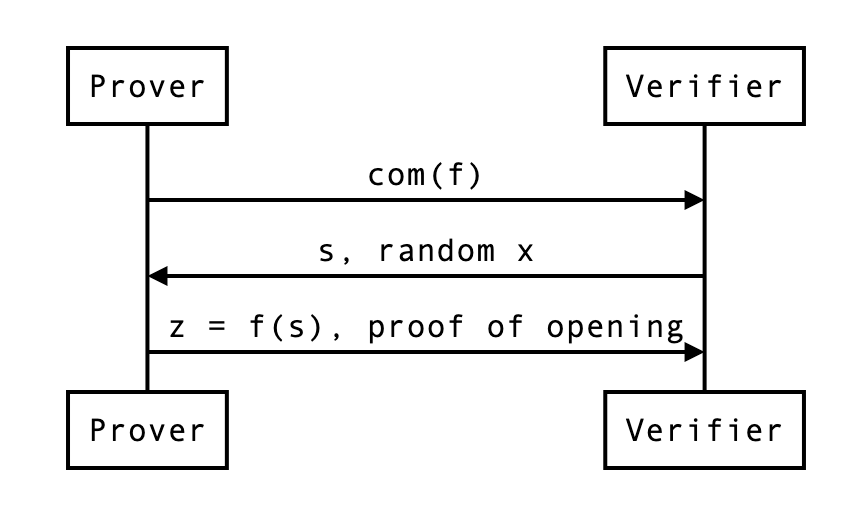
Reduced problem
首先, 证明者将所有内容一分为二. 然后, 他们使用$x$来构造这些分割的线性组合:
- $\vec{a'} = x^{-1} \begin{pmatrix}a_1 \ a_2\end{pmatrix} + x \begin{pmatrix}a_3 \ a_4\end{pmatrix}$
- $\vec{b'} = x \begin{pmatrix}b_1 \ b_2\end{pmatrix} + x^{-1} \begin{pmatrix}b_3 \ b_4\end{pmatrix}$
- $\vec{G'} = x \begin{pmatrix}G_1 \ G_2\end{pmatrix} + x^{-1} \begin{pmatrix}G_3 \ G_4\end{pmatrix}$
问题被简化为 $\langle \vec{a'}, \vec{b'} \rangle = z'$.
The actual proof
$$ \begin{align} \vec{A'} =& \langle \vec{a'}, \vec{G'} \rangle \ =& (x^{-1} a_1 + x a_3)(x G_1 + x^{-1} G_3) + (x^{-1} a_2 + x a_4)(x G_2 + x^{-1}G_4) \ =& A + x^{-2} (a_1 G_3 + a_2 G_4) + x^2 (a_3 G_1 + a_4 G_2) \ =& A + x^{-2} L_a + x^{2} R_a \end{align} $$
$$ \begin{align} \vec{z'} =& \langle \vec{a'}, \vec{b'} \rangle \ =& \langle \begin{pmatrix}x^{-1} a_1 + x a_3 \ x^{-1} a_2 + x a_4 \end{pmatrix}, \begin{pmatrix}x b_1 + x^{-1} b_3 \ x b_2 + x^{-1} b_4 \end{pmatrix} \rangle \ =& (a_1b_1 + a_2b_2 + a_3b_3 + a_4b_4) + x^{-2} (a_1b_3 + a_2b_4) + x^2 (a_3b_1 + a_4b_2) \ =& z + x^{-2} (L_z) + x^2 (R_z) \end{align} $$
验证者可以从先前的值 $z$ 以及证明者需要提供的两个标量值 $L_z$ 和 $R_z$ 重新计算 $z'$.
所以最后, 证明变成了:
- 向量 $\vec{a'}$, 其大小是 $\vec{a}$ 的一半;
- $L_a, R_a$ 曲线点(如果压缩, 则围绕两个域元素);
- $L_z, R_z$ 标量值.
我们可以更新我们之前的图表:
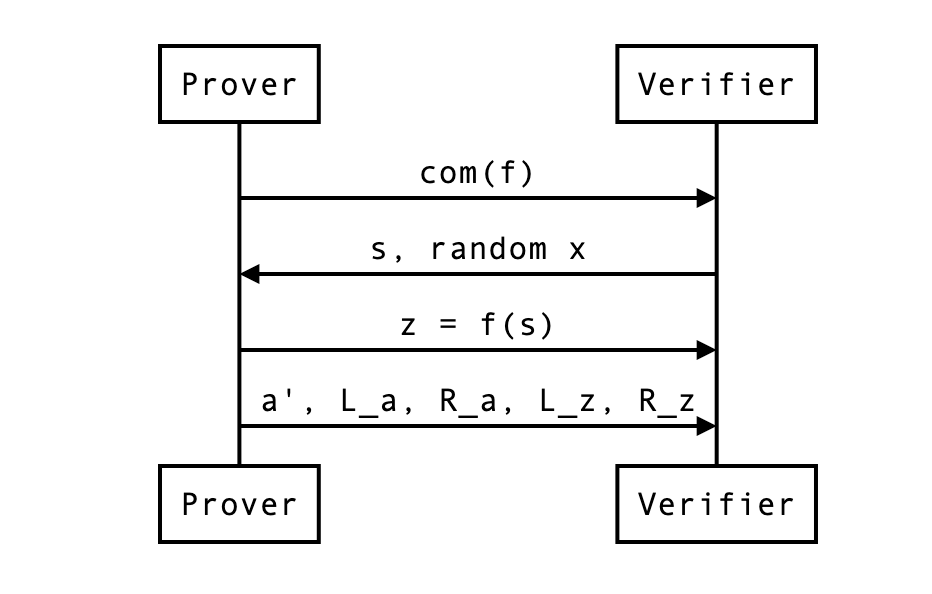
The HALO optimization
Halo 优化类似于 bulletproofs 优化, 可进一步较少 proof size. Halo 优化中, 问题转换成 $C = A + z U = \langle \vec{a}, \vec{G} \rangle + \langle \vec{a}, \vec{b} \rangle U$. 可将其 half reduce 为 $$ \begin{align} C' &= A' + z' U \ &= \langle \vec{a'}, \vec{G'} \rangle + \langle \vec{a'}, \vec{b'} \rangle U \ &= [A + x^{-2}L{a} + x^{2}R{a}] + [z + x^{-2}L{z} + x^{2}R{z}] U \ &= C + x^{-2}(L{a} + L{z}U) + x^{2}(R{a} + R{z}U) \ &= C + x^{-2}L + x^{2}R, \end{align} $$ 这里 $ L= L{a} + L{z}U $, $ R = R{a} + R{z}U $.
Halo 优化将 4 个 域元素(压缩后)优化成 2 个域元素.
下面来添加零知识(给 pedersen commitment 添加 hiding), 有 $$ \begin{align} C &= A + zU + rH \ &= \langle \vec{a}, \vec{G} \rangle + \langle \vec{a}, \vec{b} \rangle U + rH \ &= C + x^{-2}L + x^{2}R , \end{align} $$ 这里 $ L= L{a} + L{z}U + r{L}H $, $ R = R{a} + R{z}U + r{R}H $.
最后, 下图是协议在经过 $\log_{2}(n)$ 轮归约后再进行承诺打开的结果:
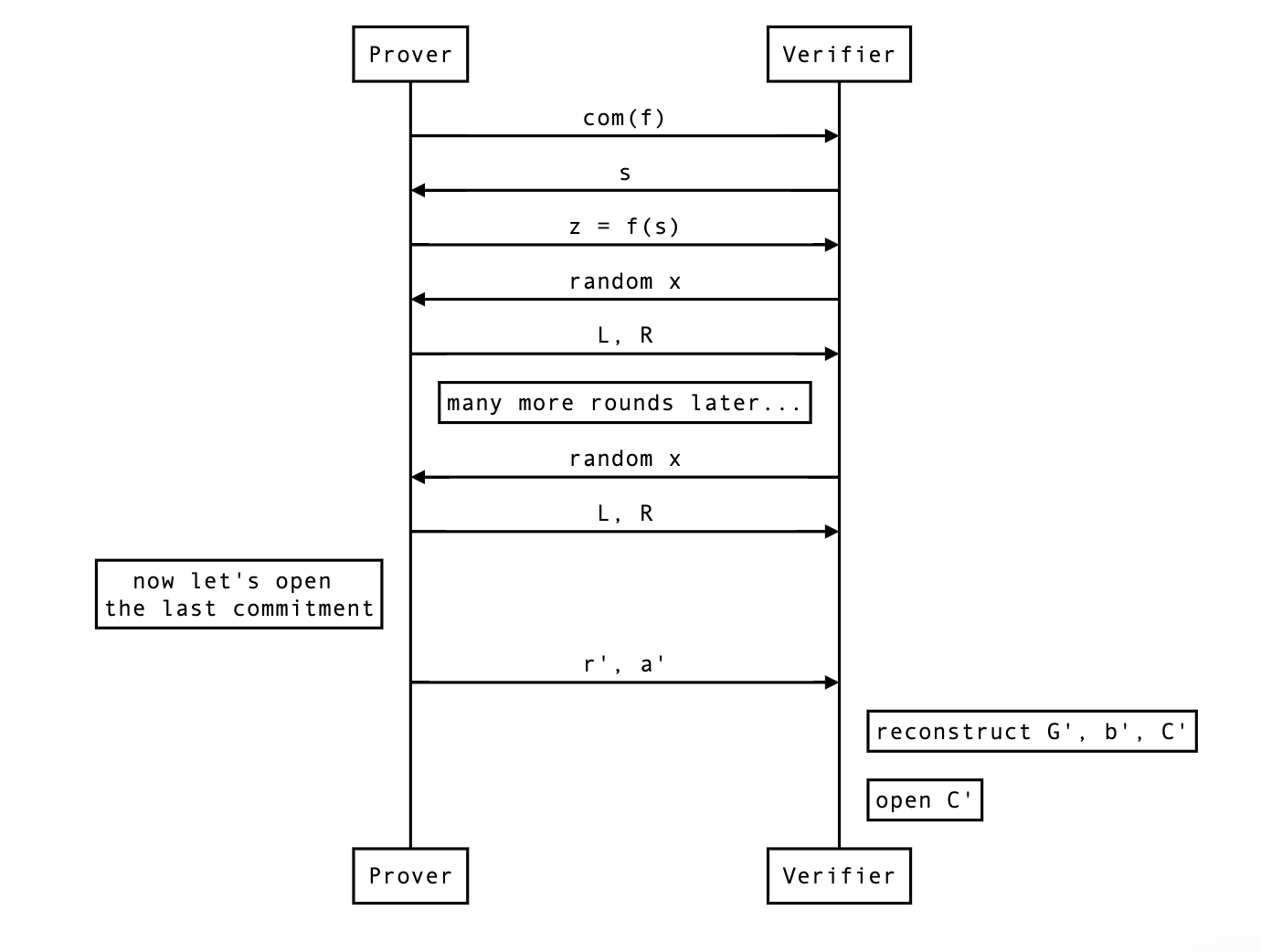
Aggregation
-
Aggregating opening proofs for several polynomials
Insight:
$$ \langle \vec{f} + v \cdot \vec{g}, \vec{x}\rangle = f(x) + v \cdot g(x) $$
-
Aggregating opening proofs for several evaluations
Insight:
$$ \langle \vec{f}, \vec{x_1} + u \cdot \vec{x_2}\rangle = f(x_1) + u \cdot f(x_2) $$
-
Double aggregation
Insight:
$$ \langle \vec{f} + v \cdot \vec{g}, \vec{x_1} + u \cdot \vec{x_2} \rangle = f(x_1) + v \cdot g(x_1) + u \cdot (f(x_2) + v \cdot g(x_2)) $$
Note that this kind of aggregation forces us to provide all combinations of evaluations, some of which might not be needed (for example, $f(x_2)$).
-
Splitting a polynomial
If a polynomial is too large to fit in one SRS, you can split it in chuncks of size at most $n$
U(S)RS
URS 由以下部分组成:
Gs: 一个任意顺序的曲线点列表, 可用于以非隐藏方式承诺一个多项式.H: 一个盲化曲线点, 可用于为多项式承诺方案添加隐藏性.
URS 是确定生成的, 可以由下面的代码生成:
fn create(depth: usize) -> Self {
let m = G::Map::setup();
let g: Vec<_> = (0..depth)
.map(|i| {
let mut h = Blake2b512::new();
h.update((i as u32).to_be_bytes());
point_of_random_bytes(&m, &h.finalize())
})
.collect();
// Compute a blinder
let h = {
let mut h = Blake2b512::new();
h.update("srs_misc".as_bytes());
// FIXME: This is for retrocompatibility with a previous version
// that was using a list initialisation. It is not necessary.
h.update(0_u32.to_be_bytes());
point_of_random_bytes(&m, &h.finalize())
};
Self {
g,
h,
lagrange_bases: HashMapCache::new(),
}
}生成算法, 见 hash-to-curve.
KZG10
$\textbf{Setup}(1^\kappa, t)$ 计算两个素数阶 $p$(提供 $\kappa$ 位安全性)的群 $\mathbb{G}$ 和 $\mathbb{G}{T}$, 使得存在一个对称双线性配对 $e:\mathbb{G}×\mathbb{G} \rightarrow \mathbb{G}{T}$ 且 $t$-$\text{SDH}$ 假设成立. 我们将生成的双线性配对群记为 $\mathcal{G}=\langle e,\mathbb{G},\mathbb{G}{T} \rangle$. 选择一个生成元 $g \in{R} \mathbb{G}$. 令 $\alpha \in{R} \mathbb{Z}{p}^{*}$ 为 $\text{SK}$, 由一个(可能是分布式的)可信权威机构生成. $\text{Setup}$ 还生成一个 $(t + 1)$ 元组 $\langle g,g^\alpha,\cdots,g^{\alpha^t}\rangle\in\mathbb{G}^{t + 1}$ 并输出 $\text{PK}=\langle\mathbb{G},g,g^\alpha,\cdots,g^{\alpha^t}\rangle$. 在构造的其余部分不需要 $\text{SK}$.
$\textbf{Commit}(\textbf{PK},\phi(x))$ 计算对次数为 $t$ 或更低的多项式 $\phi(x)\in \mathbb{Z}{p}[X]$ 的承诺 $\mathcal{C} = g^{\phi(\alpha)} \in \mathbb{G}$. 对于$\phi(x)=\sum{j = 0}^{deg(\phi)}\phi{j}x^{j}$, 它输出 $\mathcal{C} = \prod{j = 0}^{deg(\phi)}(g^{ \alpha^{j} })^{\phi_{j} }$ 作为对 $\phi(x)$ 的承诺.
$\textbf{Open}(\textbf{PK},\mathcal{C},\phi(x))$ 输出所承诺的多项式 $\phi(x)$.
$\textbf{VerifyPoly}(\textbf{PK},\mathcal{C},\phi(x))$ 验证 $\mathcal{C} \stackrel{?} {=} g^{\phi(\alpha)}$. 如果对于 $\phi(x)=\sum{j = 0}^{deg(\phi)}\phi{j}x^{j}$ 有 $\mathcal{C}=\prod_{j = 0}^{deg(\phi)}(g^{\alpha^j})^{\phi_j}$, 该算法输出 $1$, 否则输出 $0$. 注意, 这仅在 $deg(\phi)\leq t$ 时有效.
$\textbf{CreateWitness}(\textbf{PK},\phi(x),i)$ 计算 $\psi_i(x)=\frac{\phi(x)-\phi(i)}{x - i}$ 并输出 $\langle i,\phi(i),w_i\rangle$, 其中见证 $wi = g^{\psi{i}(\alpha)}$ 的计算方式与上述 $\mathcal{C}$ 类似.
$\textbf{VerifyEval}(\textbf{PK},\mathcal{C},i,\phi(i),wi)$ 验证 $\phi(i)$ 是否是由 $C$ 所承诺的多项式在索引 $i$ 处的求值. 如果 $e(\mathcal{C},g) \stackrel{?}{=} e(w{i},g^{\alpha}/g^i)e(g,g)^{\phi(i)}$, 该算法输出 $1$, 否则输出 $0$. $VerifyEval$是正确的, 因为 $$ \begin{align} e(w_i,g^{\alpha}/g^i)e(g,g)^{\phi(i)} &= e(g^{\psi_i(\alpha)},g^{(\alpha - i)})e(g,g)^{\phi(i)} \ &=e(g,g)^{\psi_i(\alpha)(\alpha - i)+\phi(i)} \ &=e(g,g)^{\phi(\alpha)} \ &=e(C,g) \end{align} $$ 因为$\phi(x)=\psi_i(x)(x - i)+\phi(i)$.
注意: $\alpha$ 是有毒的废物, 必须丢弃, 因为它可以用来破坏绑定性.
Trusted setup
更多内容, 见 How do trusted setups work?
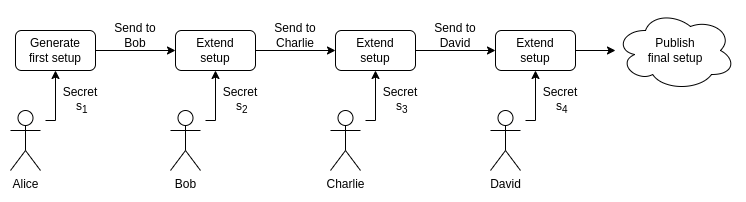
最后生成 SRS $\langle g, g^{\prod{i=0}^{k} s{i}}, \cdots, g^{\prod{i=0}^{k} s{i}^{n}} \rangle$.
更新 SRS
对于 SRS $<g, g^{s}, \cdots, g^{s^{n}} >$, 随机生成 $t$, 更新 SRS 为 $<g, g^{st}, \cdots, g^{(st)^{n}} >$.
FRI
todo
- GARUDA and PARI: Faster and Smaller SNARKs via Equifficient Polynomial Commitments 1181 浏览
- ZK Mesh:2025年7月回顾 1391 浏览
- 区块链中的数学(八十三)-- MMCS(Mixed Matrix Commitment Scheme) 1448 浏览
- 以太坊月度更新 #4:柏林互操作黑客周 1933 浏览
- 多人在线对战俄罗斯方块开发教程 2203 浏览
- 放宽未来几年对Prover的硬件要求 1149 浏览

