从头开始了解Merkle树的 LAYER 2

在本教程中，我们将从基本原理实现 Merkle Trees、Merkle 证明和 Delta Merkle 证明，使用 JavaScript。

这是 A Hackers Guide to Layer 2: Building a zkVM from Scratch. 的第一周内容。

关注 @cmpeq 以保持跟进未来的内容。

我不能创造的，我就不理解。 理查德·费曼

引言

Merkle Trees 是任何有意成为 Layer 2 开发者工具箱中最重要的工具之一。遵循费曼理解主题的方法，我们将从零开始实现 Merkle Trees，并建立 深入的 Merkle Tree 直觉，这在以后的 Layer 2 开发旅程中将是必不可少的。

发明 Merkle Trees：数据完整性

让我们想象一下，杰克想通过不可靠的互联网连接，将一个 400GB 的文件发送给他的朋友萨莉。传输这个文件需要几个小时，而萨莉想确保她收到的文件在传输过程中未被损坏或更改。

解决这个问题的一种方法是让杰克创建整个文件的数字签名，然后在文件传输完成后让萨莉验证该签名。然而，不幸的是，数字签名技术有一个属性：你想要签名的数据越长，生成数字签名就越慢，因此让杰克对整个文件进行数字签名是不实际的。

他们可以通过利用数字指纹（也称为加密散列）技术来解决这个问题。对大文件进行哈希（或数字指纹）生成一个短32字节的数字来表示被哈希的数据。最重要的是，如果你更改大文件中的任意一个字节，其指纹也会发生变化：

1. 杰克将哈希、签名和文件发送给萨莉
2. 当萨莉收到文件后，她在自己的机器上计算哈希，然后检查哈希是否与杰克数字签名的哈希匹配。

这一切都很好，但由于传输可能需要几个小时，而在此过程中很可能会出现数据损坏，萨莉不断发现她计算的哈希与杰克签名的哈希不同，杰克不得不重新发送 400GB 的文件（非常慢）。

一种解决此问题的方法是让杰克首先 将文件分割成两部分（A 和 B）并对每个部分进行哈希。 这样需要重新发送的任何数据大小将减少到 200GB 而不是 400GB。

如果杰克真的很聪明，他可以让自己只计算一个数字签名，通过签署 Hash(Hash(A)+Hash(B))（称为 根）。这样萨莉就知道 A 和 B 的哈希在传输过程中没有被修改，可以确信她收到的文件与杰克的原始文件相同。如果 A 或 B 中的任何数据被修改，Hash(Hash(A)+Hash(B)) 将不匹配杰克的原始签名。

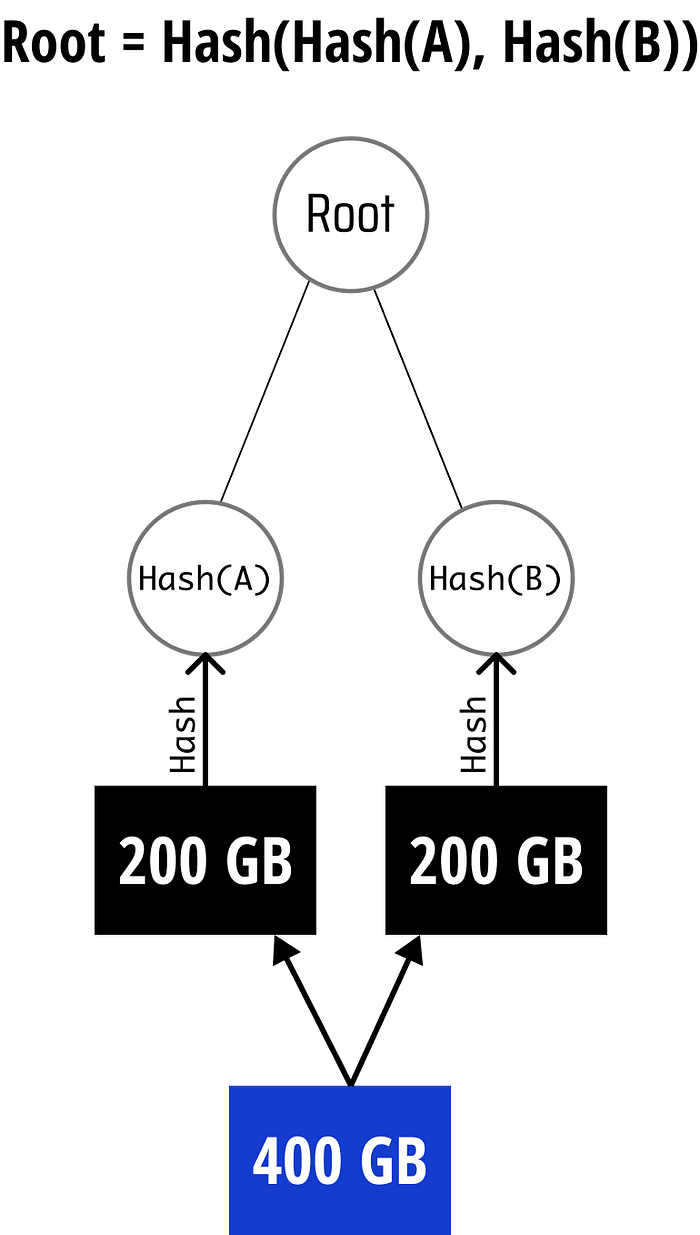
将文件分割为两部分，对每个部分进行哈希，然后将两部分的哈希组合进行哈希

其实，我们可以将文件分割得更小，以使任何需要重新发送的数据的大小更小：

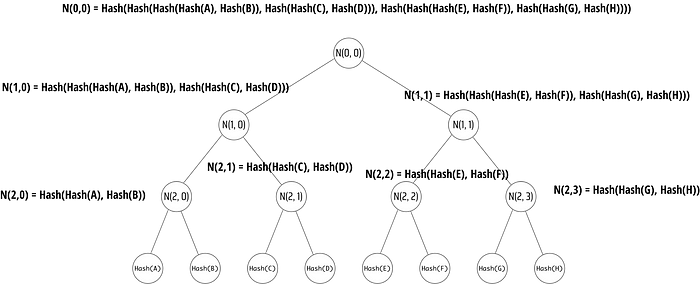
如果杰克将文件分割为 8 个部分，他将创建这样一个结构并签名 N(0,0)

分割数据并递归哈希的过程称为构建 Merkle Tree。

就像在我们的例子中，Merkle Tree 的基本原理是：

如果你修改了任何代表我们数据集的底部节点的值， 顶部节点的值也会随之改变。

底部的节点包含我们的数据集，被称为 叶子，而顶部的节点（即 N(0,0)）被称为 Merkle Root。

为了方便起见，我们可以用两个数字来标识每个节点 N：

1. 节点的 层级（顶部节点在层级 0，下面的节点层级为 1，以此类推）
2. 节点的 索引（对于索引，我们只是从左到右计数，最左侧的节点索引 = 0）

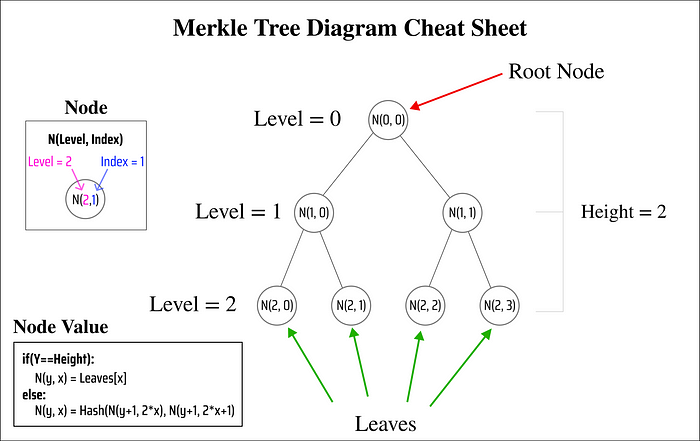
Merkle Tree 备忘单

使用我们的节点定义，我们还可以说每个节点 N(level, index)，都有两个 子节点 N(level+1, index2) 和 N(level+1, index2+1)。这是为了反映每一层的节点数量是上层节点数量的两倍。

此外，使用之前计算 Hash(Hash(A), Hash(B)) 的规则，我们可以定义每个非叶节点的值为：N(level, index) = Hash(N(level+1, index2), N(level+1, index2+1))

我们还可以定义 Merkle Tree 的 高度 为 从叶子到 Merkle Root 的距离（即计算叶节点与顶部根节点之间路径中的线数）。Merkle Tree 的叶子始终具有与树的高度相等的层级编号。

编码一个 Merkle Tree

现在我们已经发明了 Merkle Tree，我们可以通过编写 JavaScript 实现来展示我们的新知识。

首先，我们需要选择一个函数来计算我们的数字指纹。我们可以使用常见的 sha256 哈希函数来使命其计算 Hash(childA, childB)：

const shajs = require("sha.js"); // npm install --save sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}

有了哈希函数，我们可以编写一个简单的类，该类根据叶子的数据集和对应的树高度计算 merkle root：

const shajs = require("sha.js"); // npm install --save sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}

class MerkleTree {
  constructor(height, leaves){
    this.height = height;
    this.leaves = leaves;
  }
  N(level, index){
    if(level === this.height){
      // 如果层级 == 高度，该节点是叶子
      // 因此只需返回我们数据集中的值
      return this.leaves[index];
    }else{
      // 如果节点不是叶子，使用我们的定义：
      // N(level, index) = Hash(N(level+1, index*2), N(level+1, index*2+1))
      return hash(
        this.N(level+1, 2*index),
        this.N(level+1, 2*index+1),
      );
    }
  }
  getRoot(){
    // 节点 N(0,0) 始终是根节点
    return this.N(0,0);
  }
}

让我们用高度为 3，且叶子为 [1, 3, 3, 7, 4, 2, 0, 6] 的树来测试我们的 merkle tree 实现：

叶子为 [1, 3, 3, 7, 4, 2, 0, 6]且高度为 3 的树

在我们的 JavaScript 文件中，我们可以将每个叶子写为十六进制字符串，创建 MerkleTree 的新实例，并调用 getRoot 函数来计算根：

function example1(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000002", // 2
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  console.log("[EX_1] merkle tree 的根是: "+tree.getRoot());
}
example1();

如果我们运行这段代码，会得到输出：

[EX_1] merkle tree 的根是: 7e286a6721a66675ea033a4dcdec5abbdc7d3c81580e2d6ded7433ed113b7737

参考运行：CodePen Embed - Merkle Tree 示例

如果我们更改任何一个叶子（例如，将 2 改为 9），我们应该也会看到根发生变化：

function example2(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1\
    "0000000000000000000000000000000000000000000000000000000000000003", // 3\
    "0000000000000000000000000000000000000000000000000000000000000003", // 3\
    "0000000000000000000000000000000000000000000000000000000000000007", // 7\
    "0000000000000000000000000000000000000000000000000000000000000004", // 4\
    "0000000000000000000000000000000000000000000000000000000000000002", // 2\
    "0000000000000000000000000000000000000000000000000000000000000000", // 0\
    "0000000000000000000000000000000000000000000000000000000000000006", // 6\
  ];
  const tree = new MerkleTree(height, leaves);
  console.log("[EX_2] 根之前是: "+tree.getRoot());
  // 将 2 改为 9
  tree.leaves[5] = "0000000000000000000000000000000000000000000000000000000000000009";
  console.log("[EX_2] 根之后是: "+tree.getRoot());
}
example2();

如果我们运行 example2()，我们将看到输出：

[EX_2] 根之前是: 7e286a6721a66675ea033a4dcdec5abbdc7d3c81580e2d6ded7433ed113b7737
[EX_2] 根之后是: e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925

CodePen Merkle Tree 示例 2

成功！变更前的根与我们原始的根匹配，因为它具有相同的数据集，而变更后的根已更新，因为我们更改了数据集中的一个叶子。

让我们深入了解为什么更改一个叶子会改变根：

将叶子 N(3,5) 从 2 更改为 9 的影响向上冒泡到树中

• 由于我们更改了 N(3,5)，它的父节点 N(2,2) 也发生了变化，因为 N(2,2) 被定义为 N(2,2) = Hash(N(3,4), N(3,5))
• 由于 N(2,2) 发生了变化，它的父节点 N(1,1) 也发生了变化，因为 N(1,1) 被定义为 N(1,1) = Hash(N(2,2), N(2,3))
• 由于 N(1,1) 发生了变化，它的父节点 N(0,0) 也发生了变化，因为 N(0,0) 被定义为 N(0,0) = Hash(N(1,0), N(1,1))

在更新叶子时发生变化的节点称为节点的 默克尔路径。因此在这种情况下，我们可以说 N(3,5) 的默克尔路径是 [N(3,5), N(2,2), N(1,1), N(0,0)]。

要计算节点的默克尔路径，我们只需递归列出节点的祖先。（祖先 = 节点的父节点，父节点的父节点，父节点的父节点的父节点……）。

由于我们之前知道每个节点 N(level, index) 具有两个 子节点 N(level+1, index2) 和 N(level+1, index2+1)，我们可以说节点 N(level, index) 的父节点是 N(level-1, floor(index/2))。

利用这些知识，我们可以编写一个 JavaScript 函数来计算节点的默克尔路径，并检查我们之前对 N(3,5) 的观察：

function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>=0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}

console.log(getMerklePathOfNode(3,5))

当我们运行它时，日志打印出 [N(3,5), N(2,2), N(1,1), N(0,0)]：

[
  { level: 3, index: 5 },
  { level: 2, index: 2 },
  { level: 1, index: 1 },
  { level: 0, index: 0 }
]

codepen 示例 3

在实践中，我们通常会将根节点从返回的默克尔路径中排除，因为每个节点的默克尔路径都包含它，因此我们可以重写我们的函数以返回默克尔路径中所有节点，除了根节点（level>0）：

function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}

兄弟节点

在继续之前，重要的是我们要讨论默克尔树中左侧节点和右侧节点的概念。

• 我们说一个节点是 左侧节点 如果它出现在其父节点的左侧。
• 我们说一个节点是 右侧节点 如果它出现在其父节点的右侧。

根据我们对默克尔树的原始定义，我们说每个非叶子节点 N(level, index) 都有一个左子节点和一个右子节点：

• 左子节点：N(level+1, 2*index)
• 右子节点：N(level+1, 2*index + 1)

根据这个定义，我们可以看到所有左侧节点的索引都是偶数（2x），而右侧节点的索引是奇数（2x+1）。

因此：

• 如果节点 N(level, index) 的索引是偶数，我们说它的对侧兄弟节点是 N(level, index+1)。
• 如果节点 N(level, index) 的索引是奇数，我们说它的对侧兄弟节点是 N(level, index-1)。

让我们编写一个 JavaScript 函数来返回我们在树上指定的任何节点的兄弟节点：

function getSiblingNode(level, index){
  // if node is the root, it has no sibling
  if(level === 0){
    throw new Error("the root does not have a sibling")
  }else if(index % 2 === 0){
    // if node is even, its sibling is at index+1
    return {level: level, index: index+1};
  }else{
    // if node is odd, its sibling is at index-1
    return {level: level, index: index-1};
  }
}

默克尔证明

我们通常希望证明某个叶子在具有已知根的默克尔树中的 包含性。假设 Bob 想要向他的朋友 Todd 证明值 9 存在于树的叶子 N(3,5) 中，并且该树具有已知的默克尔根 R。

Bob 最简单的方法是：

1. Bob 给 Todd 一份所有叶子的列表
2. Todd 使用我们的 MerkleTree 类计算 N(0,0)
3. Todd 将 N(0,0) 与 R 进行比较，以确保它们是相同的

然而，对于大型树，这并不是很实用。如果 Bob 想要证明一棵有 1,000,000 片叶子的树中的叶子值，Bob 必须将所有 1,000,000 片叶子发送给 Todd，而 Todd 必须进行 999,999 次计算来计算根。

然而，如果我们回顾一下我们的默克尔路径图，有一种更快的方法可以做到这一点：

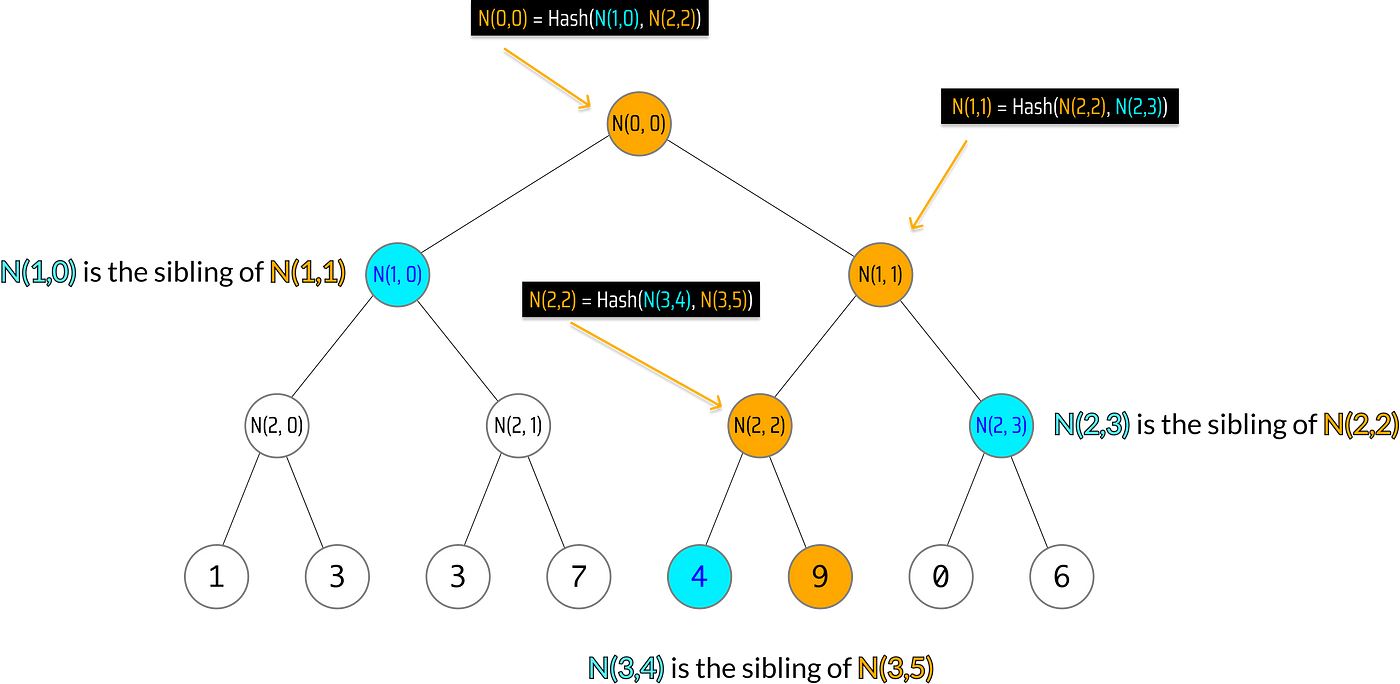
N(3,5) 的默克尔路径的 兄弟节点 用 蓝色 高亮显示

在我们的图中，我们可以看到，如果 Bob 给 Todd 提供：叶子的 值、叶子的 索引 和叶子默克尔路径上非根节点的 兄弟节点 （N(3,4)、N(2,3) 和 N(1,0)），Todd 就可以计算出根：

N(0,0) = Hash(N(1,0), Hash(Hash(N(3,4), 9), N(2,3)))

使用这种方法，对于具有 N 片叶子的树，Todd 只需要计算 log(N) 次计算，因此如果树有 1,000,000 片叶子，他只需要执行 20 次计算，而不是 999,999 次计算！

值、索引和兄弟节点一起被称为默克尔证明，因为它们是证明叶子在具有已知根的默克尔树中存在的关键成分。

让我们首先编写一个函数来计算给定节点的默克尔路径的兄弟节点：

让我们更新我们的 MerkleTree 类以包含一个 getMerkleProof 函数：

class MerkleTree {
// ...
getMerkleProof(level, index){

    // get the value of the leaf node
    const leafValue = this.N(level, index);

    // get the levels and indexes of the nodes on the leaf's merkle path
    const merklePath = getMerklePathOfNode(level, index);

    // get the levels and indexes of the siblings of the nodes on the merkle path
    const merklePathSiblings = merklePath.map((node) => {
      return getSiblingNode(node.level, node.index);
    });

    // get the values of the sibling nodes
    const siblingValues = merklePathSiblings.map((node) => {
      return this.N(node.level, node.index);
    });

    return {
      root: this.getRoot(), // the root we claim to be our tree's root
      siblings: siblingValues, // the siblings of our leaf's merkle path
      index: index, // the index of our leaf
      value: leafValue, // the value of our leaf
    };
  }
}

我们还可以编写一个函数，该函数使用证明的兄弟节点、索引和值来计算默克尔根：

function computeMerkleRootFromProof(siblings, index, value){
  // start our merkle node path at the leaf node
  let merklePathNodeValue = value;
  let merklePathNodeIndex = index;

  // we follow the leaf's merkle path up to the root, 
  // computing the merkle path's nodes using the siblings provided as we go alone
  for(let i=0;i<siblings.length;i++){
    const merklePathNodeSibling = siblings[i];

    if(merklePathNodeIndex%2===0){
      // if the current index of the node on our merkle path is even:
      // * merklePathNodeValue is the left hand node,
      // * merklePathNodeSibling is the right hand node
      // * parent node's value is hash(merklePathNodeValue, merklePathNodeSibling)
      merklePathNodeValue = hash(merklePathNodeValue, merklePathNodeSibling);
    }else{
      // if the current index of the node on our merkle path is odd:
      // * merklePathNodeSibling is the left hand node
      // * merklePathNodeValue is the right hand node,
      // * parent node's value is hash(merklePathNodeSibling, merklePathNodeValue)
      merklePathNodeValue = hash(merklePathNodeSibling, merklePathNodeValue);
    }

    // using our definition, the parent node of our path node is N(level-1, floor(index/2))
    merklePathNodeIndex = Math.floor(merklePathNodeIndex/2);
  }
  return merklePathNodeValue;
}

最后，让我们编写一个函数来验证默克尔证明：

function verifyMerkleProof(proof){
  return proof.root === computeMerkleRootFromProof(proof.siblings, proof.index, proof.value);
}

将所有内容结合在一起，我们现在有一个可以生成可以在 O(log(n)) 时间内验证的默克尔包含证明的类 🎉

const shajs = require("sha.js"); // npm install --save sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}
function getSiblingNode(level, index){
  // if node is the root, it has no sibling
  if(level === 0){
    throw new Error("the root does not have a sibling")
  }else if(index % 2 === 0){
    // if node is even, its sibling is at index+1
    return {level: level, index: index+1};
  }else{
    // if node is odd, its sibling is at index-1
    return {level: level, index: index-1};
  }
}
function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}
class MerkleTree {
  constructor(height, leaves){
    this.height = height;
    this.leaves = leaves;
  }
  N(level, index){
    if(level === this.height){
      // if level == height, the node is a leaf, 
      // so just return the value from our dataset
      return this.leaves[index];
    }else{
      // if the node is not a leaf, use our definition:
      // N(level, index) = Hash(N(level+1, index*2), N(level+1, index*2+1))
      return hash(
        this.N(level+1, 2*index),
        this.N(level+1, 2*index+1),
      );
    }
  }
  getRoot(){
    // the node N(0,0) is always the root node
    return this.N(0,0);
  }
  getMerkleProof(level, index){

    // get the value of the leaf node
    const leafValue = this.N(level, index);

    // get the levels and indexes of the nodes on the leaf's merkle path
    const merklePath = getMerklePathOfNode(level, index);

    // get the levels and indexes of the siblings of the nodes on the merkle path
    const merklePathSiblings = merklePath.map((node) => {
      return getSiblingNode(node.level, node.index);
    });

    // get the values of the sibling nodes
    const siblingValues = merklePathSiblings.map((node) => {
      return this.N(node.level, node.index);
    });

    return {
      root: this.getRoot(), // the root we claim to be our tree's root
      siblings: siblingValues, // the siblings of our leaf's merkle path
      index: index, // the index of our leaf
      value: leafValue, // the value of our leaf
    };
  }
}
function computeMerkleRootFromProof(siblings, index, value){
  // start our merkle node path at the leaf node
  let merklePathNodeValue = value;
  let merklePathNodeIndex = index;

  // we follow the leaf's merkle path up to the root, 
  // computing the merkle path's nodes using the siblings provided as we go alone
  for(let i=0;i<siblings.length;i++){
    const merklePathNodeSibling = siblings[i];

    if(merklePathNodeIndex%2===0){
      // if the current index of the node on our merkle path is even:
      // * merklePathNodeValue is the left hand node,
      // * merklePathNodeSibling is the right hand node
      // * parent node's value is hash(merklePathNodeValue, merklePathNodeSibling)
      merklePathNodeValue = hash(merklePathNodeValue, merklePathNodeSibling);
    }else{
      // if the current index of the node on our merkle path is odd:
      // * merklePathNodeSibling is the left hand node
      // * merklePathNodeValue is the right hand node,
      // * parent node's value is hash(merklePathNodeSibling, merklePathNodeValue)
      merklePathNodeValue = hash(merklePathNodeSibling, merklePathNodeValue);
    }

    // using our definition, the parent node of our path node is N(level-1, floor(index/2))
    merklePathNodeIndex = Math.floor(merklePathNodeIndex/2);
  }
  return merklePathNodeValue;
}
function verifyMerkleProof(proof){
  return proof.root === computeMerkleRootFromProof(proof.siblings, proof.index, proof.value);
}
function example4(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000009", // 9
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  console.log("[EX_4] the root is: "+tree.getRoot());
  const merkleProofOfN3_5 = tree.getMerkleProof(3,5);

  console.log("[EX_4] the merkle proof of N(3,5):\n" + JSON.stringify(merkleProofOfN3_5, null, 2));

  console.log("[EX_4] computed root: "+computeMerkleRootFromProof(merkleProofOfN3_5.siblings, merkleProofOfN3_5.index, merkleProofOfN3_5.value));
  console.log("[EX_4] verify merkle proof: "+verifyMerkleProof(merkleProofOfN3_5));
}

example4();

这将打印：

[EX_4] 根是: e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925
[EX_4] N(3,5) 的默克尔证明:
{
  "root": "e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925",
  "siblings": [
    "0000000000000000000000000000000000000000000000000000000000000004",
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"
  ],
  "index": 5,
  "value": "0000000000000000000000000000000000000000000000000000000000000009"
}
[EX_4] 计算的根: e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925
[EX_4] 验证默克尔证明: true

示例 4：生成和验证默克尔证明

增量默克尔证明

如果我们有一个根节点为 A 的默克尔树，并生成一个具有兄弟节点的默克尔证明

除了证明一个特定的叶子节点存在于默克尔树中，我们通常还希望证明将树中某个特定叶子节点的值从一个值更改为另一个值的结果。这被称为 增量默克尔证明（delta 代表变化）。

具体而言，增量默克尔证明证明了：

• 在具有默克尔根节点 A 的树中，索引 I 处存在一个值为 X 的叶子节点
• 如果你将索引 I 处的叶子的值从 X 更改为 Y，而不修改树中的其他叶子节点，则树的新默克尔根节点为 B

我们已经知道如何证明“在具有默克尔根节点 A 的树中，索引 I 处存在一个值为 X 的叶子节点”；我们只需在我们的合约上调用 getMerkleProof 函数即可。

如果我们然后修改叶子节点，假设从 9 修改为 8，我们再调用 getMerkleProof 并查看发生了什么：

function example5(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000009", // 9
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  const beforeMerkleProofOfN3_5 = tree.getMerkleProof(3,5);
  console.log("[EX_5] N(3,5)更改前的默克尔证明：\n" + JSON.stringify(beforeMerkleProofOfN3_5, null, 2));
  // 将 9 更改为 8
  tree.leaves[5] = "0000000000000000000000000000000000000000000000000000000000000008";

  const afterMerkleProofOfN3_5 = tree.getMerkleProof(3,5);
  console.log("[EX_5] N(3,5)更改后的默克尔证明：\n" + JSON.stringify(afterMerkleProofOfN3_5, null, 2));
}
example5();

这会打印：

[EX_5] N(3,5)更改前的默克尔证明：
{
  "root": "e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925",
  "siblings": [\
    "0000000000000000000000000000000000000000000000000000000000000004",\
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",\
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"\
  ],
  "index": 5,
  "value": "0000000000000000000000000000000000000000000000000000000000000009"
}
[EX_5] N(3,5)更改后的默克尔证明：
{
  "root": "99ba6856d11cd514be35ed291e86ae7957ec43d6b83270f32aaa50a8a25dc5cc",
  "siblings": [\
    "0000000000000000000000000000000000000000000000000000000000000004",\
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",\
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"\
  ],
  "index": 5,
  "value": "0000000000000000000000000000000000000000000000000000000000000008"
}

示例 5：检查修改叶子值对其默克尔证明的影响

注意到 兄弟节点是相同的 在修改前后的证明中！

记住，当我们更新一个叶子节点时，只会更改叶子节点的默克尔路径上的节点，而且 由于按定义，叶子节点的默克尔路径不包含任何兄弟节点，因此修改前后的证明具有相同的兄弟节点！

更进一步，由于两个证明都提供相同的兄弟节点和索引，验证这两个证明会证明我们仅修改了索引 I 处的叶子节点：

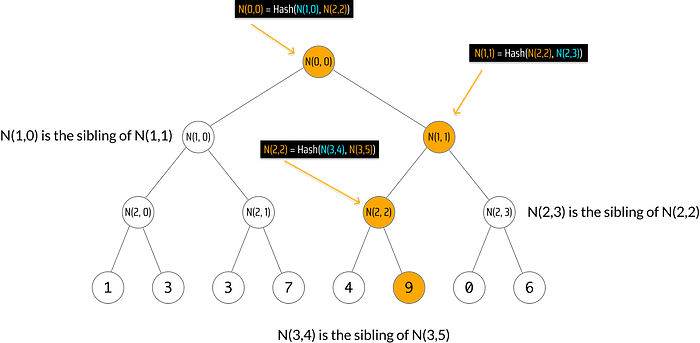
只有默克尔路径上的橙色节点发生变化，因此兄弟节点（白色）保持不变

因此，我们的增量默克尔证明需要提供：

1. 叶子的索引（对于修改前后的证明都是相同的）
2. 叶子的兄弟节点（对于修改前后的证明都是相同的）
3. 叶子的旧值（在更改之前）
4. 树的旧根（在更改之前树的根）
5. 叶子的值（在我们更改叶子值之后）
6. 树的新根（在我们更改叶子值之后）

我们可以实现一个 getDeltaMerkleProof 函数来为我们做这件事：

class MerkleTree {
  // ...
  getDeltaMerkleProof(level, index, newValue){
    // 计算索引 I 处叶子的根
    const oldLeafProof = this.getMerkleProof(level, index);
    // 从证明中计算默克尔根，替换叶子的值为新值
    const newRoot = computeMerkleRootFromProof(oldLeafProof.siblings, index, newValue);

    // 返回旧证明和新证明中的数据
    return {
      index: index,
      siblings: oldLeafProof.siblings,

      oldRoot: oldLeafProof.root,
      oldValue: oldLeafProof.value,

      newRoot: newRoot,
      newValue: newValue,
    }
  }
}

要验证增量默克尔证明，我们可以将增量默克尔证明的数据拆分为 newProof 和 oldProof，它们共享相同的兄弟节点/索引，并使用我们现有的 verifyMerkleProof 函数验证这些证明：

function verifyDeltaMerkleProof(deltaMerkleProof){
  // 将增量默克尔证明拆分为修改前和修改后的默克尔证明，重用相同的兄弟节点和索引
  const oldProof = {
    // 对于旧和新，重用相同的兄弟节点
    siblings: deltaMerkleProof.siblings,
    // 对于旧和新，重用相同的索引
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.oldRoot,
    value: deltaMerkleProof.oldValue,
  };

  const newProof = {
    // 对于旧和新，重用相同的兄弟节点
    siblings: deltaMerkleProof.siblings,
    // 对于旧和新，重用相同的索引
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.newRoot,
    value: deltaMerkleProof.newValue,
  };
  return verifyMerkleProof(oldProof) && verifyMerkleProof(newProof);
}

让我们将这一切组合在一起，看看效果：

const shajs = require("sha.js"); // npm install --save sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}
function getSiblingNode(level, index){
  // 如果节点是根，则没有兄弟节点
  if(level === 0){
    throw new Error("根节点没有兄弟节点")
  }else if(index % 2 === 0){
    // 如果节点是偶数，其兄弟节点在 index+1
    return {level: level, index: index+1};
  }else{
    // 如果节点是奇数，其兄弟节点在 index-1
    return {level: level, index: index-1};
  }
}
function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}
class MerkleTree {
  constructor(height, leaves){
    this.height = height;
    this.leaves = leaves;
  }
  N(level, index){
    if(level === this.height){
      // 如果 level == height，节点是一个叶子节点，
      // 因此只需返回我们的数据集中的值
      return this.leaves[index];
    }else{
      // 如果节点不是叶子，使用我们的定义：
      // N(level, index) = Hash(N(level+1, index*2), N(level+1, index*2+1))
      return hash(
        this.N(level+1, 2*index),
        this.N(level+1, 2*index+1),
      );
    }
  }
  getRoot(){
    // 节点 N(0,0) 始终是根节点
    return this.N(0,0);
  }
  getMerkleProof(level, index){

    // 获取叶子节点的值
    const leafValue = this.N(level, index);

    // 获取叶子节点的默克尔路径上的节点的级别和索引
    const merklePath = getMerklePathOfNode(level, index);

    // 获取默克尔路径上节点的兄弟节点的级别和索引
    const merklePathSiblings = merklePath.map((node) => {
      return getSiblingNode(node.level, node.index);
    });

    // 获取兄弟节点的值
    const siblingValues = merklePathSiblings.map((node) => {
      return this.N(node.level, node.index);
    });

    return {
      root: this.getRoot(), // 我们声称是我们树的根
      siblings: siblingValues, // 我们的叶子默克尔路径的兄弟节点
      index: index, // 我们的叶子的索引
      value: leafValue, // 我们叶子的值
    };
  }
  getDeltaMerkleProof(level, index, newValue){
    // 计算索引 I 处叶子的根
    const oldLeafProof = this.getMerkleProof(level, index);
    // 从证明中计算默克尔根，替换叶子的值为新值
    const newRoot = computeMerkleRootFromProof(oldLeafProof.siblings, index, newValue);

    // 返回旧证明和新证明中的数据
    return {
      index: index,
      siblings: oldLeafProof.siblings,

      oldRoot: oldLeafProof.root,
      oldValue: oldLeafProof.value,

      newRoot: newRoot,
      newValue: newValue,
    }
  }
}
function computeMerkleRootFromProof(siblings, index, value){
  // 从叶子节点开始我们的默克尔节点路径
  let merklePathNodeValue = value;
  let merklePathNodeIndex = index;

  // 我们沿着叶子的默克尔路径向上移动到根，
  // 在沿途使用提供的兄弟节点计算默克尔路径的节点
  for(let i=0;i<siblings.length;i++){
    const merklePathNodeSibling = siblings[i];

    if(merklePathNodeIndex%2===0){
      // 如果默克尔路径中当前节点的索引是偶数：
      // * merklePathNodeValue 是左边的节点，
      // * merklePathNodeSibling 是右边的节点
      // * 父节点的值是 hash(merklePathNodeValue, merklePathNodeSibling)
      merklePathNodeValue = hash(merklePathNodeValue, merklePathNodeSibling);
    }else{
      // 如果默克尔路径中当前节点的索引是奇数：
      // * merklePathNodeSibling 是左边的节点
      // * merklePathNodeValue 是右边的节点，
      // * 父节点的值是 hash(merklePathNodeSibling, merklePathNodeValue)
      merklePathNodeValue = hash(merklePathNodeSibling, merklePathNodeValue);
    }

    // 使用我们的定义，当前路径节点的父节点是 N(level-1, floor(index/2))
    merklePathNodeIndex = Math.floor(merklePathNodeIndex/2);
  }
  return merklePathNodeValue;
}
function verifyMerkleProof(proof){
  return proof.root === computeMerkleRootFromProof(proof.siblings, proof.index, proof.value);
}
function verifyDeltaMerkleProof(deltaMerkleProof){
  // 将增量默克尔证明拆分为修改前和修改后的默克尔证明，重用相同的兄弟节点和索引
  const oldProof = {
    // 对于旧和新，重用相同的兄弟节点
    siblings: deltaMerkleProof.siblings,
    // 对于旧和新，重用相同的索引
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.oldRoot,
    value: deltaMerkleProof.oldValue,
  };

  const newProof = {
    // 对于旧和新，重用相同的兄弟节点
    siblings: deltaMerkleProof.siblings,
    // 对于旧和新，重用相同的索引
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.newRoot,
    value: deltaMerkleProof.newValue,
  };
  return verifyMerkleProof(oldProof) && verifyMerkleProof(newProof);
}
function example6(){
  const height = 3;
  const leaves = [\
    "0000000000000000000000000000000000000000000000000000000000000001", // 1\
    "0000000000000000000000000000000000000000000000000000000000000003", // 3\
    "0000000000000000000000000000000000000000000000000000000000000003", // 3\
    "0000000000000000000000000000000000000000000000000000000000000007", // 7\
    "0000000000000000000000000000000000000000000000000000000000000004", // 4\
    "0000000000000000000000000000000000000000000000000000000000000009", // 9\
    "0000000000000000000000000000000000000000000000000000000000000000", // 0\
    "0000000000000000000000000000000000000000000000000000000000000006", // 6\
  ];
  const tree = new MerkleTree(height, leaves);

  const deltaMerkleProofOfN3_5 = tree.getDeltaMerkleProof(3,5, "0000000000000000000000000000000000000000000000000000000000000008");
  console.log("[EX_6] 将 N(3,5) 的值从 9 更改为 8 的增量默克尔证明：\n" + JSON.stringify(deltaMerkleProofOfN3_5, null, 2));
  console.log("[EX_6] 验证增量默克尔证明： "+verifyDeltaMerkleProof(deltaMerkleProofOfN3_5));
}

example6();

运行这段代码打印：

[EX_6] 将 N(3,5) 的值从 9 更改为 8 的增量默克尔证明：
{
  "index": 5,
  "siblings": [\
    "0000000000000000000000000000000000000000000000000000000000000004",\
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",\
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"\
  ],
  "oldRoot": "e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925",
  "oldValue": "0000000000000000000000000000000000000000000000000000000000000009",
  "newRoot": "99ba6856d11cd514be35ed291e86ae7957ec43d6b83270f32aaa50a8a25dc5cc",
  "newValue": "0000000000000000000000000000000000000000000000000000000000000008"
}
[EX_6] 验证增量默克尔证明：true

示例 6：增量默克尔证明

成功！我们现在发明了默克尔树、默克尔证明和增量默克尔证明的核心概念。

更重要的是，凭借这一直觉，我们能够利用对默克尔证明工作的全面理解来实施这些证明的变体，以创造有用和高效的数据存储以便在我们的Layer2 协议中使用。

在下一个教程中，我们将为大型稀疏默克尔树构建一个高效的默克尔树数据库，编写一个仅使用 O(log(N)) 存储的追加唯有默克尔树，并研究一些允许我们合并树和证明历史状态的默克尔证明变体。

感谢我们的赞助商 OAS 和 QED，你可以在推特上关注 OAS @OASNetwork

关于作者 - 在推特上关注 @cmpeq 或查看我的 关于页面。

访问 QED https://qedprotocol.com

• 原文链接： medium.com/@carterfeldma...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～