共识算法解读:泛化的中本聪共识PHANTOM
- Po
- 发布于 2020-06-03 12:26
- 阅读 6077
PHANTOM在DAG数据结构的区块链上,将中本聪共识进行了泛化,它不需要事先设定出块间隔等限制,因此也接触了中本聪共识对拓展性-安全性的权衡。采用贪心算法,也便于实现,并且安全性也被严格证明了。
引言
比特币运行了十几年都非常的安全,但是饱守诟病的问题就是它的吞吐量太低了,这也是由它的安全模型即最长链规则决定的。最长链规则要求所有的诚实节点能迅速接收到新创建的区块,因此,必须要等到一个区块完全传递到所有节点才能创建下一个块,并且保证了创建的"孤块"(orphan blocks)非常的少。
那么从这个角度上来讲,就是吞吐量和安全之间必须进行权衡,而比特币协议的最长链规则限制了这个权衡规则,有没有更好的思路呢?
答案就是,在并行的同时保障安全。以色列的研究团队,在2020年的《PHANTOM and GHOSTDAG A Scalable Generalization of Nakamoto Consensus》一文中,提出了在借助于有向无环图DAG,使用一个参数k(后面具体介绍k的来历)来限定网络的安全容忍度的同时,且保障了并行出块(因为新区块,会引用所有DAG的叶子节点作为父块,而不是直接丢弃网络中没有到主链上的快,然后先出块再排序)。比如下图,B,C,D,E可以并且出块,且V是新出的块,它需要引用J,M,L。
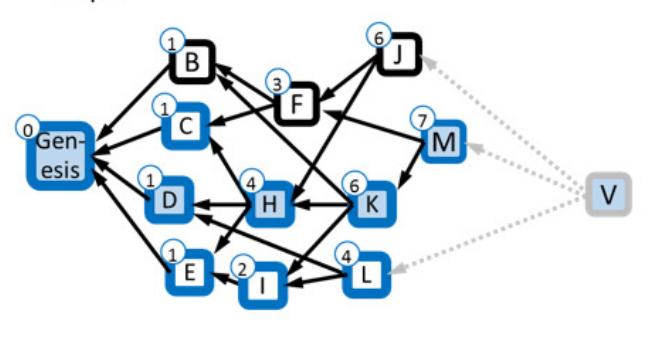
直观上来看,具体的思路是怎样的呢?
类比比特币,定义网络的延迟是D,那么为了保证没有分叉,那么D这个时间段内就不能再产生块了,也就是每秒出块速度得很慢,我们可以认为是肯定小于k个块。具体而言就是网络时延1秒的话,1秒内最多产生1/600个块(10分钟出一个块)。
那么把这个概念拓展一下就是,在DAG图中的块,需要保证在一个出块的周期内(此处指的是没有明显的前后引用关系),最多出k个块。
PHANTOM协议的思路也就由此而来,它需要保证在同一个出块阶段内,最多出(k+1)个块。为了保证这点,它先定义了anticone函数:对于一个块B,查找它所在的DAG图中与他没有直接或间接引用关系(也就是在DAG图中不能访问到的)的块的数目。比如说下图中区块G,在整个DAG图中它不能访问到B,F,I,H,K所以anticone(B)=B,F,I,H,K。并定义|anticone(B)|为总共块的数目,也即5.
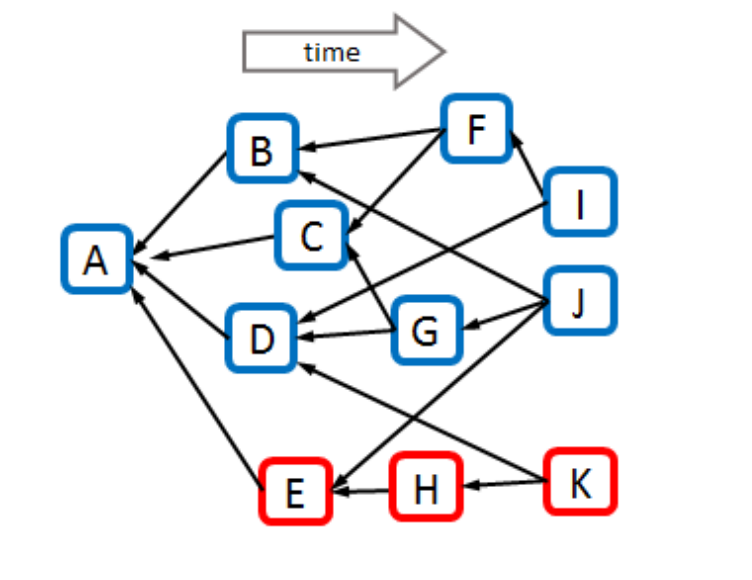
<center>图 2</center>
然后就需要求解一个最大k-cluster子DAG图的问题,记为MCSk:

简单来说就是这样一个问题:
- 输入:DAG
- 输出:一个最大子DAG图S’,S‘中任一区块B的anticone在S’的块的数目不超过k。
举图2中最大3-cluster的例子,蓝色的块构成的DAG图就是最终找到的MCS3。很容易验证任何一个蓝色的块都满足|anticone(B)|≤3,比如anticone(G)=B,I,F。而anticone(E)=(B, C, D, F, G, I),有6个块,不满足。并且可以看出k=3时,实际上保证了每一个出块间隔内最多产生3+1个块(因为不同阶段的明显可以通过引用关系直接确定),也就是说k决定了每个出块间隔最多出k+1个块。
但是实际上,这个问题是个NP-hard问题,所以作者采用简单的贪心法来构建MCSk,也就是先把之前满足MCSk条件的DAG图创建好,然后新创建的区块再去找到满足它的条件的块,判断是否满足MCSk条件,并加入到MCSk中。
找到MCSk之后,就可以进行确定区块的全局序了。
整个DAG区块的序按照如下方式确定:
- 确定好MCSk,然后把它标记为蓝色的,其他的块标记为红色的
- 对MCSk按照拓扑排序(也就是DAG图中从创世区块开始,根据边的关系,后面被访问到的就排后面),这样就确定了一个主链;然后再对蓝色块中,没有在主链上的逐个加入到序列中;最后把红色的区块,按照拓扑排序加入进来。
听起来是不是头晕了,还是举个简单的例子吧,假设k=3,我们来按照下图构建全局的序(V为虚拟区块便于理解):
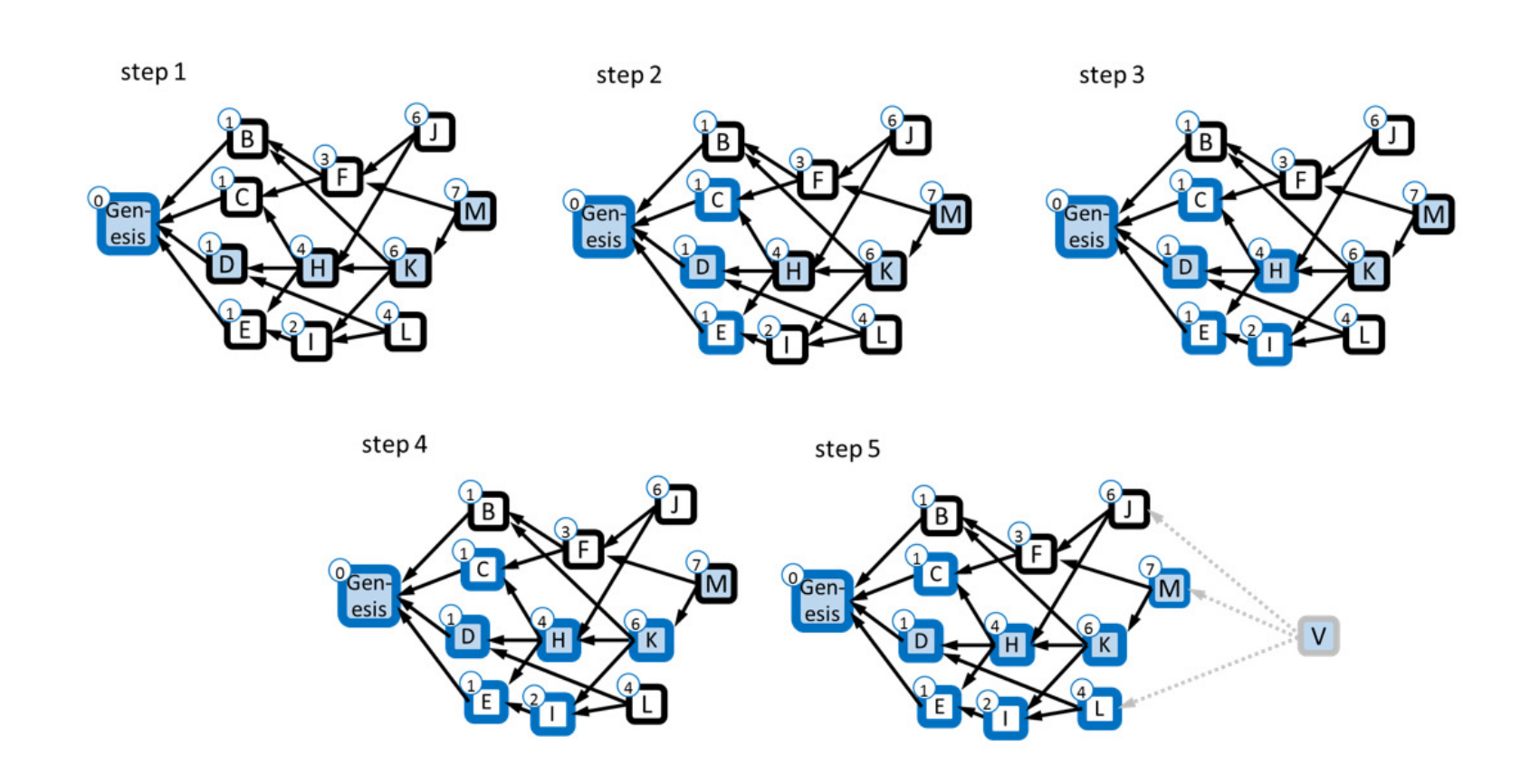
- 从M开始(因为它包含的过去的区块最多),再选K(因为F的过去的区块只有3个),依次选取H,D,genesis,从而构建出主链
- 然后再迭代地构建MCSk
- 首先访问D,过去的只有Genesis,所以添加创世区块到蓝色块中
- 访问H,然后判断C,D,E的|anticone|是否小于等于3,发现都满足,所以添加C,D,E
- 访问K,同理添加H,I
- 访问M,添加K,因为|anticone(F)|=4,所以不能添加F
- 然后添加M
- 排序
- 根据任意的拓扑排序算法确定蓝色集合的序,比如Genesis,D,E,C,I,H,K,M
- 将红色区块进行拓扑排序并加在后面,逐个加上B,F,L,J
- 因此总体的序为:Genesis,D,E,C,I,H,K,M,B,F,L,J
- 最后按照交易在区块内部的出现的顺序进行排序,就可以确定交易的序了
感兴趣的可以看下,形式化的算法如下:

实际上,我们发现如果把k设为0,那么这就是中本聪共识。
拓展性又如何呢?
在此,我们定义协议的拓展性指的是,在不牺牲安全门限(恶意节点控制的最小算力比例)的同时,还能提高区块的生成速度。
作者证明了PHANTOM可以保证安全门限的下限是1 /2 · (1 − δ),而δ由k来控制,k越大δ越小。
增加区块产生速度λ:安全门限不会随着λ增大而增大,但是同时受到节点带宽的限制,比如带宽1M的话,一个区块大小是1M,那么λ最多可以提升到每秒出一个块。
提升安全性:提升安全门限,需要提升k,但是会增大确认时间
存活性(确认时间):区块被篡改的风险,随着不断出块,指数级下降。假设网络延迟7秒,可以安全地设置k=16,在攻击者算力为α ≤ 0.25,被篡改的概率为ϵ = 0.1% 时,交易确认时间仅为45秒。并且确认时间,对网络延迟增大不敏感。
总结
PHANTOM在DAG数据结构的区块链上,将中本聪共识进行了泛化,它不需要事先设定出块间隔等限制,因此也接触了中本聪共识对拓展性-安全性的权衡。采用贪心算法,也便于实现,并且安全性也被严格证明了。
但是具体的实验数据,目前还是没有,需要进一步的验证...
- Minimmit:简单快速的共识 741 浏览
- 密码朋克人物传之《比特币核心开发者 Gavin Andresen》 1700 浏览
- 密码朋克人物传之《比特币先驱 Hal Finney》 1458 浏览
- 比特币的诞生 1989 浏览
- 密码朋克人物传之《密码朋克思想领袖 Timothy C. May》 962 浏览
- 密码朋克人物传之《比特币创造者 Satoshi Nakamoto》 2262 浏览
- 密码朋克人物传之《B-money提出者 Wei Dai》 1166 浏览
- 区块链 101:超越区块链(第二部分) 1738 浏览
- 51%攻击:概念、风险与预防 934 浏览
- 中本聪的代码与其人 1135 浏览
- Alpenglow:Solana 的重大共识重写 3466 浏览
- 2025年学术资助计划介绍 1637 浏览

