优化数值结果 DLC 创建

TLDR;

在数值结果的情况下，适配器签名的创建速度显著加快。

引言

我们最近 宣布 我们在 P2PDerivatives 应用程序 中实现了所谓的 数值分解。这项技术使得减少所需适配器签名的数量成为可能，以覆盖具有相同支付值的结果范围（如果你没有理解这句话的含义，第一部分是为你准备的。如果你理解了，可以跳过）。虽然这在空间上是一个巨大的改进（在 DLC 的两个对等方之间交换的签名更少），但 Matthew Black 向我们报告说，适配器签名的创建速度显著变慢。在本文中，我们将首先简要回顾数值分解，然后解释为何会发生这种缓慢，最后展示我们是如何显著减少它的。

数值分解 DLC

在使用数值分解之前，我们的Oracle（报告BTC/USD汇率）只是签署代表某个时刻价格的字符串。现在假设我们有Alice和Bob想要基于BTC/USD价格进入DLC，条件如下：

• 价格高于 $50000，Alice得到全部，
• 价格在 $40000 和 $50000 之间，有一个线性支付函数，将总保证金分配给双方，
• 价格低于 $40000，Bob得到全部。

如果他们想确保可以在 $0 和 $1000000 之间的比特币价格上正确关闭他们的合同，他们将不得不创建100000个不同的适配器签名。这在生成这些签名、交换它们和存储它们方面都相当不切实际。

使用数值分解后，我们的Oracle现在分别签署每个数字。例如，如果价格是 $45000（假设Oracle被设置为报告8位数字），它将分别释放对数字 '0' '0' '0' '4' '5' '0' '0' '0' 的签名。

这如何帮助Alice和Bob？例如，为了覆盖 $10000 以下的结果范围，他们只需要创建适配器点，将前四个数字设置为零（'0' '0' '0' '0'），而忽略剩下的四位。因此，他们只需要一个适配器签名，而不是10000个来覆盖 $0-$9999 的范围。

请注意，实际上，我们的oracle签名的是结果值的二进制表示（而不是像示例中那样使用十进制），因为这被认为更加高效。你还可以在 DLC 规范库 中找到更多细节。

速度降低

那么，为什么在切换到数值分解后适配器签名的创建速度会下降呢？要理解这一点，我们需要稍微深入一下适配器签名的创建过程（只涉及加法和乘法，不用担心！）。

适配器签名

在这里，我们将非常快速地回顾适配器签名的概念，想要更详细描述的可以查看 我们之前的文章。适配器签名是一种用秘密加密的签名，我们可以证明在解密后（或知道这个秘密后）我们可以为给定消息获得一个有效签名。在 ECDSA 下，消息 m 的签名 s 的适配器签名 s’ 是这样创建的：

给定 x 一个私钥和 t 一个秘密

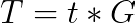
t 的公共图像（也称为适配器点）

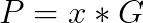
x 的公钥

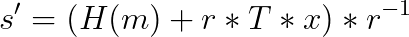
我们将略去验证部分（如果你对此感兴趣，请再次查看 我们的适配器系列），但是如果知道秘密 t，我们可以按照如下方式获得有效签名 s：

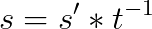
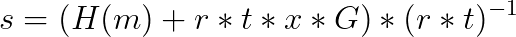
这是针对 m 的有效 ECDSA 签名。

对于DLC，我们使用oracle的签名作为创建适配器签名的秘密。值得注意的是，最初没有任何参与方知道实际的秘密。并且大多数为DLC创建的适配器签名的秘密（希望）永远不会被揭示，因为oracle应该为每个事件释放一个签名。因此，在实践中，双方计算Oracle可能释放的所有可能签名的图像（也称为签名点），并用它们加密他们对每个支付交易的签名。请注意，oracle使用的是 BIP340 Schnorr 签名，其方程看起来像这样：

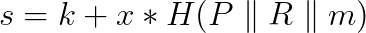
因此，对于每个可能的 m（代表DLC的可能结果的值），双方将按照如下方程创建适配器点 S：

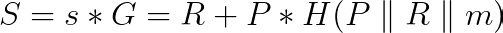
请注意 S 仅使用公开已知值创建（回想一下 DLC oracle 需要在每个事件前发布 R 值）。

数值分解下的适配器签名

现在，为了理解为什么使用数值分解创建适配器签名的速度更慢，让我们看看发生了什么变化。使用数值分解时，我们用所有签名图像的总和作为加密秘密。因此，如果我们有一个将释放签名 s0,s1,s2,…,s7 的oracle，我们将使用下列方式构建的适配器点 S：

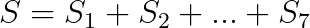
其中每个 Sx 的构建如前所述。

这依赖于 Schnorr 签名的线性特性，使我们能够接下来使用以下方式解密适配器签名：

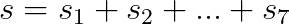
因此，我们可以看到，与“常规”DLC的主要区别在于我们需要计算一个点的总和。

利用分解和多 Oracle 的适配器签名

使用与分解类似的方法，可以创建利用来自多个 oracle 的签名点加密的适配器签名。这是通过简单地对每个 oracle 的签名点求和实现的。假设 oracle A、B 和 C 和数值分解，我们可以按如下方式为每个 oracle 计算签名点：

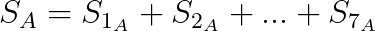
然后我们可以通过对签名点求和来计算聚合 S：

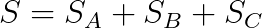
理解

要理解在使用数值分解和多个 oracle 的情况下，适配器签名创建为什么会很慢，我们需要注意到 椭圆曲线（EC）乘法 的计算成本比加法要高得多。这是因为 EC 乘法是通过重复将一个点加到它自身来执行的。因此，要计算：

其中 A 是一个 EC 点，实际上我们做的是：

虽然存在计算它们的算法优化（如 二倍并加法），但普遍而言，EC 点的乘法仍然比加法更昂贵。

现在，让我们再次查看在数值分解情况下计算签名点的方程：

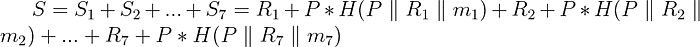
我们可以看到我们有七个乘法（或者说我们有的非ces或数字一样多）。如果我们另外使用了多 oracle，这个数字将乘以 oracle 的数量。因此我们可以假设，适配器点计算中乘法数量的增加是适配器签名计算缓慢的原因。为了确认这个假设，我们对使用 5 个 oracle 和每个 oracle 20 个 nonce 创建单个适配器签名的速度进行了基准测试。以下是结果：

完整的适配器签名计算

6,444,640 ns/iter (+/- 628,459)

来自签名点的适配器签名计算

280,801 ns/iter (+/- 62,948)

签名点计算

6,222,608 ns/iter (+/- 667,325)

我们可以看到，确实，大部分时间是花在计算签名点上。

优化

现在我们了解了为什么计算成本高，让我们看看如何改善这种情况。

提取因子

回顾一下数值分解情况下签名点计算的方程：

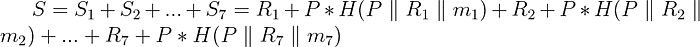
我们仍然有七个乘法，但请注意它们都涉及到公钥 P。因此，我们可以使用你可能很久以前学过的东西，因式分解！而且幸运的是，它同样适用于椭圆曲线。所以我们可以将我们的方程重写为：

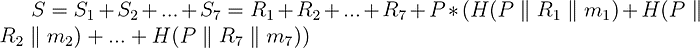
现在我们只有一个 EC 乘法操作！

为了验证这一点，我们针对“常规”版本对这个因式分解的版本进行了基准测试。我们期望我们的因式分解优化在增加的 nonce 数量下性能不断变好。我们通过在不同数量的 nonce 和 5 个 oracle 的情况下基准测试这两个版本来验证这一点。以下图表显示了结果：

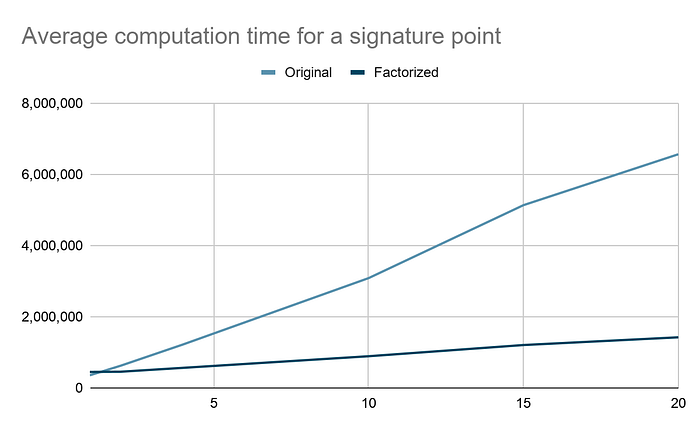
我们可以看到，尽管原始版本在使用单个 nonce 时稍有更好的表现，但在使用两个 nonce 时，我们的优化版本已经更快了。

虽然这似乎已经是一个不错的改进，但我们仍然需要根据计算的适配器签名的数量执行与 EC 乘法相同的操作。

预计算

为了进一步减少创建大量签名点时的 EC 乘法数量，我们需要改变策略。请回想一下每个“最终”结果的签名点是通过将每个数字的预期值所计算的签名点的总和。通过预先计算每个数字每个可能值的签名点集，最大数量的 EC 乘法将变为 nb_nonces * nb_outcome_per_nonce，在这之后我们只需要执行加法。因此，如果我们有两个 nonce 和每个 nonce 两个结果，我们需要预先计算：

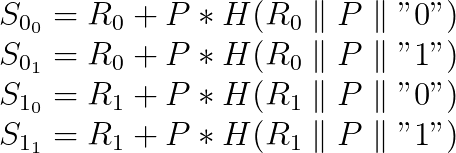
然后我们可以按如下方式计算所有可能的组合签名点：

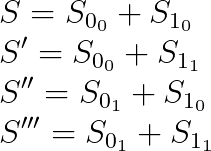
在这个示例中，我们并没有减少 EC 乘法的数量，因为我们预计算了 4 个签名点，并且我们总共有 4 个可能结果。然而，例如，当有 10 个 nonce 时，而不是执行 2¹⁰=1024 次 EC 乘法，我们只需进行 20 次。

为了看到这一优化的影响，我们对使用 10 个 nonce、3 个 oracle 和每个 nonce 两个结果的所有可能结果的签名点创建进行了基准测试，分别为“原始”版、因式分解版和预计算版。

原始版

1,935,444,337 ns/iter (+/- 187,182,386)

因式分解版

518,583,393 ns/iter (+/- 19,961,490)

预计算版

142,026,577 ns/iter (+/- 6,604,498)

我们可以看到，正如预期的那样，预计算版本的性能明显更好。

记忆化

为了进一步优化，我们应该注意到在上述情况下，我们重新计算了一些加法。例如，在计算结果值为“0 0 0 0 0 0 0 0 0 0”和“0 0 0 0 0 0 0 0 0 1”的签名点时，值“0 0 0 0 0 0 0 0 0”的中间签名点被计算了两次。通过缓存中间值，我们可以大幅减少执行的加法数量。大致来说，我们应用的记忆化算法工作如下：

1. 使用 nonce R0 计算值“0”的签名点
2. 使用 nonce R1 和值“0”添加到前一个获得的值，计算“0 0”的签名点
3. 使用 nonce R2 和值“0 0”添加到前一个获得的值，计算“0 0 0”的签名点
4. …

一旦我们计算出结果值为“0 0 0 0 0 0 0 0 0 0”的签名点，我们可以回溯并重用计算出的“0 0 0 0 0 0 0 0 0”的签名点，以计算值“0 0 0 0 0 0 0 0 0 1”的签名点。以此类推，直到我们计算出所有可能的结果值的签名点。

使用与上述相同的基准测试，我们得到以下结果：

记忆化

42,049,313 ns/iter (+/- 2,844,778)

这使得算法速度提高了3倍以上！我们可以预期，随着非ces数量的增加，性能提升也会增加。

并行化

提高算法性能的另一个常见技巧是并行化操作，使得可以在不同内核上运行它们。虽然并不总是可能或值得这样做，但在我们情况下，我们可以轻松地并行化每个 oracle 的签名点计算以及它们的聚合。因此，我们可以不按顺序地计算：

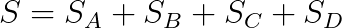
而是可以计算（其中 || 表示并行）：

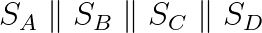
然后

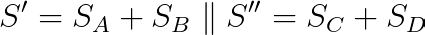
最后

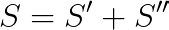
（请注意，在实际情况下，执行操作的顺序是非确定性的）

使用之前相同的基准测试，我们得到以下结果：

记忆化 + 并行化

24,089,747 ns/iter (+/- 5,290,419)

大约是 2 倍的提升。如果我们增加 oracle 的数量，提升也会增加。

结论与未来工作

通过减少 EC 乘法的数量和应用并行化，我们能够显著改善签名点的计算。由于DLC是一种点对点协议，预计适配器签名将在终端用户设备上计算，因此减少所需的计算资源变得非常重要。尽管并行化不 всегда 是可能的，但预计算和记忆化方法已经显示出良好的效果。

我们将在不久的将来把这些优化实现到我们的 P2PDerivatives 应用程序 中，以期进一步提升用户体验。

最后，Nadav Kohen 提到我们可以通过调整 BIP340 中提到的批量验证算法进一步改善。来自 Lloyd Fournier 的 提议，用索引替代消息哈希也可能带来进一步的收益。我们希望在后续文章中进一步讨论这些内容，所以别忘了 关注我们的Twitter 以了解最新动向！

致谢

感谢 Lloyd Fournier、Ichiro Kuwahara、Nadav Kohen 和 Matthew Black 的有用建议和讨论，这导致了本文所述的各种优化。

• 原文链接： medium.com/crypto-garage...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～