EIP-4844 Proto-Danksharding 为何使用 KZG ，它如何工作的？

EIP-4844 Proto-Danksharding 使用 KZG 承诺。它的作用是什么，实际是如何工作的？

我们正在朝着一个以 rollup 为中心的路线图前进。

随着模块化区块链基础设施的不断成熟，大多数活动将发生在 Optimism、Arbitrum、zkSync、Starknet、Scroll 等 rollup 上，而不是以太坊主网，以太坊的关键角色将转向为这些 Layer 2 提供安全层，而不是在一种单一设计中以太坊独自处理一切。

尽管 Layer 2 可以通过将执行任务转移到 Layer 1 区块链之外来降低交易的Gas费用，但如果我们想要实现大规模采用，交易成本仍然是显著的。让我们从调查 L2 的交易成本开始。

Rollup Fees = L2 执行费用 + L1 安全费用

来自 rollup 交易的费用可以分为两部分：

• L2 执行费用：在 L2 上执行此类交易的成本
• L1 安全费用: 在以太坊主网上发布交易数据（作为 Calldata，稍后将进一步讨论）以确保“数据可用性”

数据可用性对于乐观 rollup（ORUs）和零知识 rollup（ZKRUs）都很重要，因为我们需要能够查看和收集数据，以便生成欺诈证明或在排序器恶意/离线时提供应急方案。

历史上，L1 安全费用占用户支付的总费用的 80–90%，这一点可以从下面图表中 Optimism 的交易费用中得到证明。由于 Optimism 在 2023 年 6 月推出的 Bedrock 升级 引入了优化后的数据压缩，L1 安全费用显著下降到整体费用的约 50%。

然而，当链上活动增加，更多 L2 上线时，L1 安全费用可能会再次飙升。社区正在寻找一种解决方案，以降低 rollup 交易中的主要成本因素。

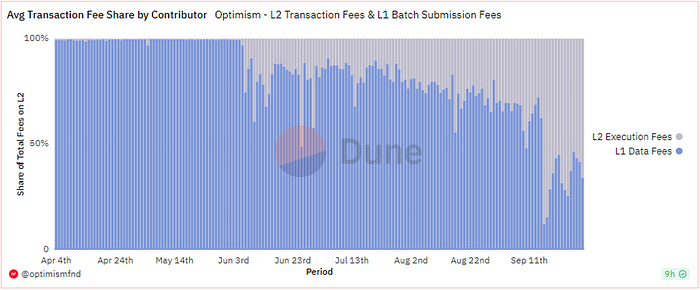
来源: Dune Analytics

长期解决方案将是完整的数据分片，但这需要大量的时间和工作才能实施全面的分片。因此，我们需要一个临时解决方案，帮助我们实现部分数据分片的优势，而这就是 EIP-4844 及其“blob 交易”和 Proto-Danksharding 等术语发挥作用的地方。

什么是 EIP-4844：Blob 交易？

要理解二进制大对象（BLOBs），首先需要简要了解以太坊区块链中各种存储空间的类型：

• 存储： 用于存储状态变量，最昂贵
• 内存： 用于存储仅在函数执行期间使用的变量，成本低于存储
• 栈： 用于加载变量和中间值，成本与内存相似
• Calldata： 用于存储函数参数，只读，在所有存储位置中最便宜

Rollup 利用 calldata 发布交易数据，这是最便宜（相对而言）的存储位置。但正如前面提到的，尽管如此，它仍然占据了 L2 整体交易成本的显著部分，如果我们想要引入大规模采用的应用程序则节省成本的程度仍不够。

EIP-4844 是一项以太坊改进提案，介绍了 Blob 交易。以太坊将允许将 blob 附加到正常的以太坊 L1 交易（就像附加副车），而不是 rollups 将交易数据作为 calldata 发布。这将通过允许每个区块 4–6 个 blobs，使数据可用性增加至 ~0.5 Mb/L1 块（每个 blob 可包含 128Kb 数据）。

blob 数据将在共识层（CL）节点中存储几周的时间（参数可以调整）。在此之后，blob 数据将被丢弃。因此，资源使用是有限的，这一点是有益的，因为所需的资源不会随着 rollups 持续发布 blob 数据而不断上升。

Blob 交易的生命周期

1. 用户正常在 L2 上发送交易
2. L2 排序器将交易打包并使用 blob 交易提交到 L1，所有 blob 数据都嵌入其中
3. Beacon 链提议者接受交易并构建包含 blobs 副车的执行负载
4. 执行负载作为正常交易保留在 L1，共识层（CL）节点会在预定时间内持有 blobs 数据

Engine API 处理共识层与执行层之间的通信以及 blobs 数据在网络中的分发

5. 在这个阶段结束时，blob 数据将从 CL 节点被丢弃（因为 L2 有足够的时间在整个期间下载/查看/争议数据）

注意：以太坊不为这些 L2 交易数据提供永久性存储，处理它的责任在于 L2（其中一种方法是 L2 将这些 blob 数据永久存储在 IPFS 上）

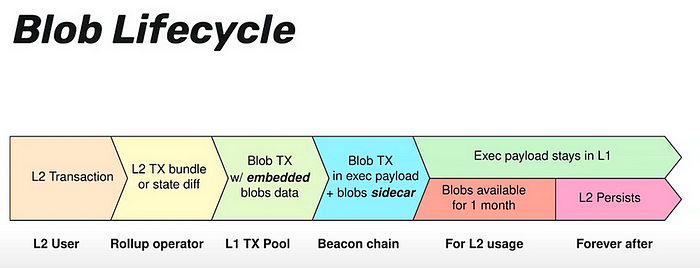
来源： @Protolambda

L2 为 EIP-4844 需要做什么改变？

为了利用 EIP-4844 引入的新 blob 交易类型，L2 需要采用以下更改：

• 批量提交者： 需要更新批量提交者代码，以便能够提交新的 blob 数据格式到 L1
• 验证器： 验证器代码需要更新，以便能够检索 blob 数据并验证 L2 状态转换
• L1 证明： L1 证明需要更新，以访问 blob 数据，以便在 L1 上能够验证 L2 状态转换

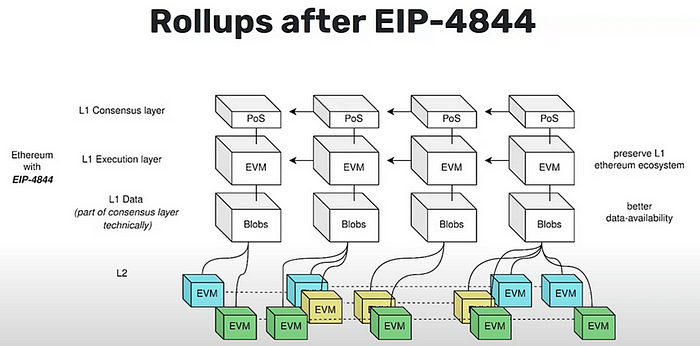
来源： @Protolambda

Blob 交易是什么样的？

看下面的图片，Blob 交易类型具有与 EIP-1559 相同的功能，但消息中添加了两个新扩展。

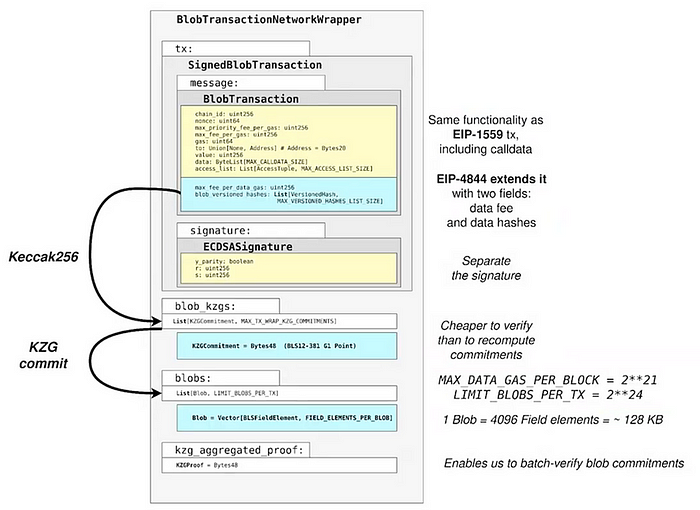
• i) max_fee_per_data_gas：因为我们现在需要一个适应这种新 blob 数据存储的经济模型；以及
• ii) blob_versioned_hashes：这些是指向单独 blobs 的“指针”。它们是 _blobkzgs 的哈希，这是 blobs 的 KZG 承诺。

注意：KZG 承诺为 48 字节，由于 EVM 更自然地处理 32 字节值，EIP-4844 使用版本化哈希而不是直接使用 KZG 来表示数据。

在接下来的部分中，我们将详细阐述这两个新扩展，重点关注 KZG 承诺的机制，因为这是实现 EIP-4844 的密码学技术。

EIP-4844 的费用市场

费用市场相对直观易懂。由于 CL 节点现在需要做额外工作（在预定时间内存储 blob 数据），他们需要获得相应的奖励。因此，将会有一个由数据Gas计量的单独费用市场。类似于 EIP-1559 的调整，EIP-4844 将设置一个目标使用量。

当网络观察到 blob 使用量超过目标 blob 使用量（即 L2 发送大量 blob 数据）时，数据费用将在下一个区块中增加，反之，当 blob 使用量低于目标时，数据费用则会降低。

这种费用调整机制鼓励更均匀地分布 blob 的使用。

多项式承诺方案与凯特-扎韦鲁查-戈德堡（KZG）承诺

理解一个复杂概念最直观的方法是通过简单的例子进行说明，并在必要时填补理论解释的空白。

这里所有的数学都是简化过的（过于简化），目标是让任何基本了解区块链的人能理解发生的事情，如果你对更技术性的分析感兴趣，我在最后的参考部分中包含了相关文章和视频。

让我们从一个示例开始，假设我们想在一个 blob 交易中包含一条消息，比如字符串 “BLOBS”。使用 KZG 承诺要经过几个步骤

步骤 0：准备

步骤 1：承诺

步骤 2：打开

步骤 3：验证

步骤 0.1 — 将数据转换为点

• 我们想使用数学而不是字符，这样就可以处理承诺和证明。我们需要将字符转换为点。
• 我们可以通过将字符编码为数字来完成这一步，考虑 i) 字符的位置（x 坐标）；以及 ii) 字符本身（y 坐标）。
• 假设我们为 y 坐标使用下面的简单编码表（此处简化了）。

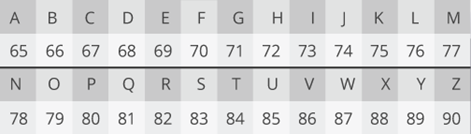
• “BLOBS” 中的第一个字母 “B” 将在 (1,66) 点，因为它是第一个字母，而 “B” 对应于我们表中的 66。
• 同样，第二个字母 “L” 由 (2,76) 表示…
• “BLOBS” 可以用五个点表示！ [(1,66), (2,76), (3,79), (4,66), (5,83)]

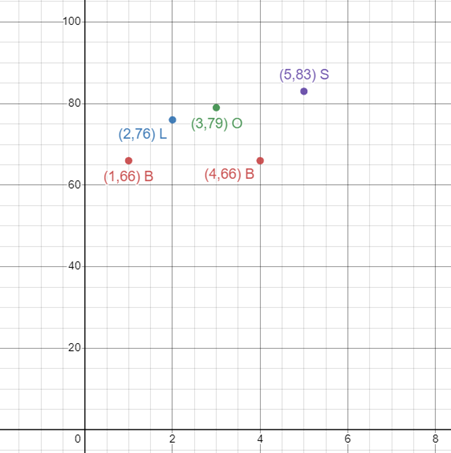
步骤 0.2 — 将点转换为多项式

多项式是只涉及加法、减法、乘法和变量的非负整数指数运算的表达式。例如：y = 2x³ — x + 10。

• 现在我们需要找到一个通过所有点的多项式，该多项式在某种意义上是我们编码的原始消息的 ID。请注意，原始消息及其对应多项式都不应该被公开知晓（它可以很好地与 zk rollups 一起使用）。
• 目标： 如果我想验证某人（证明者）确实知道原始消息，我可以通过让他证明他知道这个多项式来完成，所有这些都不需要我（水印）知道原始消息或多项式。
• 我们利用一种称为拉格朗日插值的技术，以便不需要知道它是如何工作的。你只需要知道这种技术为我们提供了一个通过我们所有点的多项式。在我们的 “BLOBS” 示例中，多项式将如下。

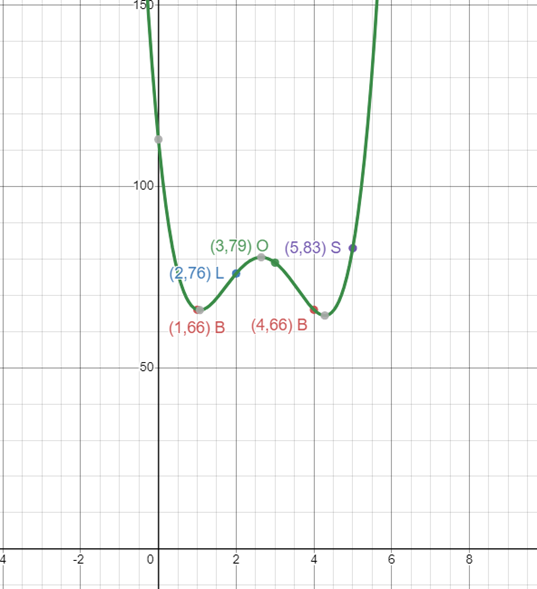
• 总结起来，多项式可以表示为

f(x) = a₀x⁰ + a₁x¹ + a₂x² + a₃x³ + … 其中 a ₙ 是 xⁿ 的系数。_

步骤 0.3 — 在一个秘密值处评估多项式

• 我们想要在不揭示实际数据/多项式的情况下生成证明，因此我们不能选择原始数据点（例如 L(2,76)）来评估多项式。
• 解决这个问题的简单方法是，我们可以在 x=4.5 处评估之前的多项式示例。鉴于 x 坐标表示字符的位置，应该是一个整数。在 x = 4.5 处评估多项式并不会泄露任何数据（甚至我们可能包括的任何潜在数据，因为我们永远不会有一个 x 坐标为 4.5 的数据点）。
• 但我们还没有完成。如果攻击者知道我们用来评估多项式的点，他们可能会克服并突破我们的系统。
• 解决方案“很简单”，就是在一个随机秘密数字上评估多项式！确实如此，但获取一个不公开的随机数字是一个困难的问题。
• 这就使我们需要 KZG 召唤仪式，它会生成我们正在寻找的秘密值。

步骤 0.4 — KZG 召唤仪式

一次性可信的设置

• KZG 召唤仪式的目的是生成一个没有人知道的秘密，这可以用于将来评估任何消息的多项式。
• 这是一个可信的设置，这是一个只做一次的数据生成过程，每次运行密码学协议时都必须使用。
• 被称为可信的设置意味着我们信任对仪式有贡献的各方的诚实。虽然在区块链领域“受信任”听起来很可怕，但该仪式具有 “1-of-N” 信任假设，也就是说，只要有一个诚实的参与者遵循该过程并抛弃他的秘密贡献，该秘密仍然会保持安全和未知，即使其他所有人都共谋。因此，只要贡献者的数量足够大，可信的设置就可以被认为是“无信任的”。
• 以太坊的 KZG 召唤仪式于 2023 年 1 月启动，并持续了两个月，总共贡献超过 141,000 次。以下是 KZG 召唤仪式网页的截图。

• 我们收到了超过 141,000 个社区贡献的秘密，这太棒了！但我们不是只在寻找一个秘密吗？我们如何实际上“聚合”每个人的输入，并将所有这些贡献转化为有用的东西，以便能够继续进行多项式评估步骤？

结构化参考字符串的构建

• 我们将从贡献中创建一个结构化参考字符串（SRS）。这将在返回多项式评估时非常有用。SRS 的结构为 [S0, S1, S2, S3, … ,Sn]，n 取决于我们希望如何设置我们的 SRS。
• 假设我们的 SRS 停止在 n=4，即 [S0, S1, S2, S3,S4]，并且第一个秘密由 S1 表示为 2，那字符串将是 [S10, S11, S12, S13, S14] à [20, 21, 22, 23, 24] à [1, 2, 4, 8, 16]。
• 假设第二个秘密 S2 是 3，我们将把字符串中的每个项与新的秘密乘以其对应的幂，因此我们得到 [1* S20, 2* S21, 4* S22, 8* S23, 16* S24] à [1*30, 2*31, 4*32, 8*33, 16*34] à [1*1, 2*3, 4*9, 8*27, 16*81] à [1, 6, 36, 216, 1296]。
• 第三个秘密是 7，那么我们只需重复相同的乘法过程，最终获得新的字符串 [1, 42, 1764, 74088, 3111696]。
• 这不是实际用于评估多项式的最终 SRS 形式，但在我们可以继续进行之前还需要一些工具。到目前为止，我们所做的是将每个人的秘密贡献凝聚成一个字符串。

模运算

• 正如你可能注意到的，在我们之前的示例中秘密显然是 42（只需查看第二项 S1）。这根本不是一个秘密！！
• 我们需要一些额外的工具来帮助我们隐藏秘密。首先，我们需要使用模运算。
• 理解模运算的简单方法是求取除法的余数。
• (20 + 4) mod 5 是 4（因为 4 是 24 除以 5 的余数），(31 + 5) mod 12 是 0（因为 36 可以被 12 整除）。
• 从本质上讲，它创建了一个像钟表一样的循环（钟表是 mod 12）。如果我们将任何两个数字相加并通过 modulo 5“包裹结果”，你总会得到 {0, 1, 2, 3, 4} 之一作为输出。
• 这对我们是有用的。如果我们使用模运算表示数字，很难知道哪个是原始数字。如果我告诉你在取模 5 后输出是 1，你不能判断输入是 1、6、16 还是 23851。
• 另一个重要概念称为 生成元。如果 group 中的所有元素都可以通过对某个特定的 group 元素重复应用 group 操作获得，那么这个元素即为 生成元。直观而言，生成元 就像一种原材料，可以用来重建集合中的所有其他项，就像我们如何加/减 1 来获得所有整数。
• 让我们看看我们的群体 {0, 1, 2, 3, 4}，这是任何两个整数相加的结果，再通过模 5“包裹”得到的。1 在这个组中是一个生成元，因为我们可以通过将 1 自己相加并计算余数来获得整个集合（2 也是这个组的生成元，你可以自己尝试证明）。

• 生成元 也存在于一些乘法群中，例如我们有一个在模 5 下的整数乘法群 {1, 2, 3, 4}。2 是这个组的生成元，只需尝试将 2 自身相乘并取模 5，你将得到 {1, 2, 3, 4} 中的所有元素。

• 还有许多更正式的符号和定义，包括阿贝尔群和循环群。它们往往会让读者（包括我自己在阅读时）感到恐惧，因此我在上述解释中省略了这些正式性。只需记住 生成元 的角色，因为它将在后面的讨论中再次出现。
• 我们离目标更近了一步，但记住我们一直在处理多项式和点？我们希望做相同的模运算，但使用点和多项式。

椭圆曲线与有限域生成

• 我们的目标是在当前利用多项式做同样的把戏。我们从一个形式为 y² = x³ + ax + b 的多项式开始，这称为椭圆曲线。你不需要知道我们如何得出这个形式，但你会发现它具有一些我们可以利用的良好特性。

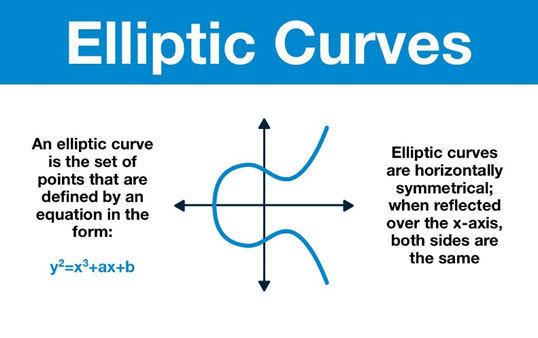
来源: @LogarithmicRex

• 还记得我们是如何应用模运算来创建“循环”的么？我们可以通过创建有限域在椭圆曲线中做同样的事。
• 我们识别 x 为整数的所有点，并“绑定”曲线在 0 和 max_value 之间，用 max_value 进行 Evaluating。我们创建了一个所有结果点都将在该区域内的“域”。
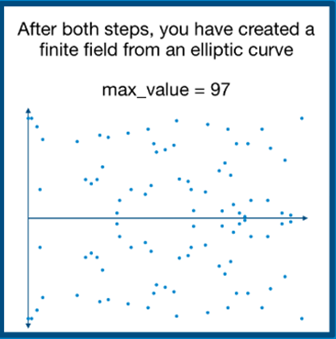
• 然后我们绘制出所有点（下面右下角的图），我们知道存在 生成点 G （此部分的解释超出范围），你需要知道的唯一信息是存在 生成点 G，这就是能够重建有限域中所有点的基础点，类似于之前对模运算中 生成元 的讨论。生成的有限域看起来似乎是随机的，但所有的点实际上是通过 G 相互关联的。

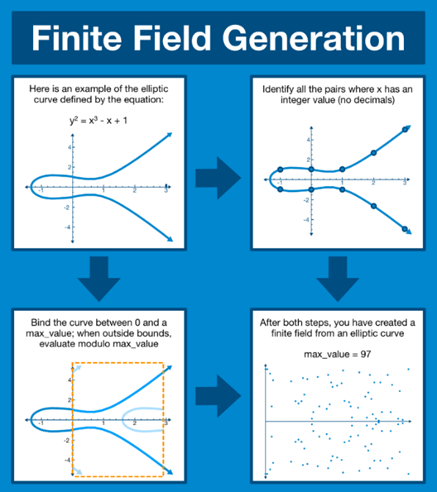
来源: @LogarithmicRex

回到我们的结构化参考字符串

• 记得我们有 SRS 将所有秘密贡献凝聚成一条字符串吗？我们在之前讨论中错过了一个关键步骤，直接使用 [S10, S11, S12, S13, S14] 不对，我们需要将 SRS 中的每一项与 生成点 G 乘起来，使得 SRS 变成 {G*[S0], G*[S1], G*[S2], G*[S3], G*[S4]}。
• 等等，如果 G 是生成点（我们在有限域上的基点），那么任何整数计算 G 乘以就像将基点自加 Sn 次，结果 G*[Sn] 也将是椭圆曲线上的一点！即使所有人都知道 SRS，我们的 秘密 S 仍然安全，因为从数学上讲，通过查看 G*[Sn] 几乎不可能取回 S（类似于告诉你 k mod 5 的结果是 1，但你无法推断出 k 是 1 还是 16 或 23851）。

来源: @LogarithmicRex

• 现在我们已经准备好了，进入下一步。

步骤 1 — 承诺

• 现在我们已从准备阶段中做好了一切准备。

- 用于拟包含的陈述的多项式 create，此内容为证明者所知，但不是所有人

f(x) = a₀x⁰ + a₁x¹ + a₂x² + a₃x³ + …

• 结构化参考字符串，这是公开的（但没有人知道什么是 S）

{G*[S0], G*[S1], G*[S2], G*[S3], …}

• 我们椭圆曲线的有限域，这是公开的。
• 考虑证明者出来说：我知道原始消息，我可以通过表明我知道从编码消息插值得到的多项式来证明这一点。
• 证明者可以通过计算 f(S)，该多项式是我们正在处理的，但没有人知道 S 是什么！证明者如何承诺多项式？
• 证明者首先将 SRS 应用于多项式。

回想： f(x) = a₀x⁰ + a₁x¹ + a₂x² + a₃x³ + …

• 应用 SRS，我们得到承诺 Cf

= a₀*G*[S⁰] + a₁*G*[S¹] + a₂*G*[S²] + a₃*G*[S³] + … = {a₀*[S⁰] + a₁* [S¹] + a₂* [S²] + a₃* [S³] + …} * G = f(S) * G

• 证明者已承诺他正在使用的多项式！注意 C 𝒻 = f(S) * G 也是椭圆曲线上的一个点，因为 G 是生成点，但承诺本身对此秘密 S 没有透露任何信息，因此 S 已被保密。

步骤 2 — 开放

• “开放”这个术语可能会有些令人困惑。简言之，此步骤涉及验证者要求证明者提供一个在验证者选择的有限域中的随机特定点 z 的评估证明。
• 证明者需要向验证者提供开放三元组（OT）= (z, f(z), Cₕ)。z 是验证者选择的，f(z) 证明者可以轻松计算，因为他拥有多项式，但 Cₕ 又是什么呢？

我们从 f(x) — f(z) 开始。

f(z) — f(z) = 0，我们知道 x = z 必须是根，因此存在 h(x) 使得

f(x) — f(z) = (x-z) * h(x) h(x) = (f(x) — f(z)) / (x-z) 证明者拥有多项式 f(x)，给定 f(z) 和 (x-z) 可以很容易计算，证明者可以相应地找到 h(x)，如果他确实拥有他所声明的内容，h(x) 被称为商多项式。

现在我们拥有 h(x)，我们需要使用 SRS 重新生成承诺，方法与步骤 1 中对 f(x) 的操作相同，因此我们得到的承诺是： C ₕ = h(S) * G。

• 随着 OT 的准备好，证明者将信息返回给验证者。

步骤 3 — 验证

• 请记住，验证者不知道 f(x) 和 h(x) 的值，但需要检查证明者发送的 OT 是否有效，即证明者返回的 f(z) 的值（用 c 表示）是否确实是 f(z) 的实际值。
• 验证者可以验证以下内容：

回忆 h(x) = (f(x) — f(z)) / (x-z) 如果 c 确实是 f(z)，那么

h(x) = (f(x) — c) / (x-z)

重新排列这些项，我们得出

(x-z) * h(x) = f(x) — c

在秘密点 S 处评估等式：

(S-z) * h(S) = f(S) — c

将两边都乘以生成点 G：

(S-z) * h(S)*G = f(S)*G — c*G

记住我们有 C 𝒻 = f(S) * G 和 C ₕ = h(S) * G ，替换它们，我们得到

(S-z) * C ₕ = C 𝒻 — c*G

• 这就是验证者需要验证的内容，但 S 是我们的秘密且未知！验证者需要一个额外的工具来完成任务。

椭圆曲线配对

• 完成验证阶段的最终技术环节是椭圆曲线配对。
• 数学超出范围且相当复杂（我在参考部分中包含了维塔利对椭圆曲线配对的文章），我们需要知道的是，它可以用于以下步骤：

回顾验证者试图验证以下内容

(S-z) * C ₕ = C 𝒻 — c*G

相反，可以使用椭圆曲线配对等式，验证者现在可以验证

e((S-z) * C ₕ , G) = e(C 𝒻 — c*G, G)

利用配对图的双线性特性，我们可以将其改写为：

e(C ₕ ,(S-z)*G) = e(C 𝒻 — c*G, G)

e(C ₕ ,S*G — z*G) = e(C 𝒻 — c*G, G)

• 请记住，我们的障碍是 S 是未知的，但 S*G 是已知的，因为它在我们的 SRS 中！
• 验证者具备利用椭圆曲线配对完成验证的所有所需信息。

为什么我们使用 KZG 承诺而不是 Merkle 证明？

有些人可能会好奇，为什么会引入 KZG，而不是使用 Merkle 证明，这是因为 KZG 具有以下优良特性：

• 验证者需要重构多项式，而重计算整个 Merkle 证明的计算，而 KZG 可以利用开放而无需完全重构多项式。
• Merkle 证明将需要一个完整的欺诈证明方案，即为了检查承诺是否真实，你必须下载所有数据，即使你只想验证一笔交易，而 KZG 在这方面已经是加密保证。
• KZG 的证明大小与多项式的大小无关，始终仅为一个组元素。验证所需的操作与多项式的大小无关，总是需要两个组乘法和两个配对，而无论多项式的阶数如何。这意味着证明大小是恒定的！
• KZG 方案隐藏了多项式，而在 Merkle 证明方案中，整个多项式与验证者共享，没有任何信息是秘密的。

Proto-Danksharding 之后的下一阶段：完成的 Danksharding

在 EIP-4844 实施后，下一阶段将是完全的 Danksharding。这将使轻节点能够以显著比完整节点更便宜的硬件来贡献以太坊的安全性和吞吐量，因为轻节点可以简单地抽样数据而无需下载整个区块。然而，这需要进一步的工作，包括数据可用性抽样和纠删编码。

数据可用性抽样（DAS）

数据可用性抽样使得节点可以下载总数据的一小部分随机选定的子集，如果节点能够成功下载样本，他们可以高信心（从数学上）确认所有数据是可用的。

然而，DAS 尚未实现，因为如果我们仅以简单的方式进行抽样，实际上很有可能你并未抽样到丢失的数据块，因此我们无法确认所有数据可用。使 DAS 得以实施的基础也是首先编码数据，以便当可用 50% 数据时，可以重构整个数据集，这种技术称为纠删编码。

纠删编码

纠删编码使用冗余数据来保护数据的丢失，它是一种数据存储和传输方法。Reed-Solomon 代码用于以太坊的纠删编码。它用冗余信息扩展给定的数据集。这是通过在数据上拟合多项式并在额外点进行评估来完成的（与我们的 “BLOBS” 示例中的步骤 0.1 非常相似）。

这里的额外步骤是，将原始信息块（还记得我们如何将字符串中的字母转变为一堆点）扩展为更多点（生成冗余信息）。然后我们可以找到一个通过所有点的多项式。只要我们能够抽样可用的 50% 数据，就可以确定原始多项式（从而获取所有编码信息）。

最后的备注

在我们能够收获全面的 Danksharding 的好处之前，还有很多工作要做，但即将到来的坎昆升级中的 Proto-Danksharding是一个重要的踏脚石，可以让我们享受部分改善，并为全面的 Danksharding 打下基础。

同时，观察现有和即将到来的 L2 如何适应这一新升级，如 L2 如何处理数据的可检索性（检索历史数据的能力）也将是十分有趣的。由于以太坊在 EIP-4844 之后将不再永久存储 L2 交易数据，现在各个 L2 需要找到最优解决方案以永久存储其交易数据。

感谢 @domothy 对这项工作的反馈。

资源：

1. Scaling Ethereum Summit | EIP-4844 在 44 分钟内（或更短）— Protolambda
2. EIP-4844
3. KZG 多项式承诺 — Dankrad Feist
4. KZG 多项式承诺 — OpenSense
5. KZG 在实践中的应用：多项式承诺方案及其在扩展以太坊中的使用 — Scroll
6. PCS 可信设置 — Inevitable Ethereum
7. 探索椭圆曲线配对 — Vitalik
8. 数据可用性抽样：从基础到开放问题 — Paradigm
9. Reed-Solomon编码的本质 — Franceso
10. 纠删编码 — Etherscan

• 原文链接： medium.com/@tommy_chan/e...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～