以太坊PBS中的密封投标 - 对提案者-构建者动态的影响
- thogiti
- 发布于 2024-06-06 20:31
- 阅读 1409
本文探讨了以太坊在采用权益证明共识机制后,提出者-构建者分离(PBS)结构及其对经济激励的影响。文章分析了拍卖机制,尤其是第一价密封拍卖(FPSBA)和第二价密封拍卖(SPSBA)对以太坊网络经济学的影响,通过模拟不同的估值分布,提供了对优化拍卖策略的洞见,强调了拍卖机制对以太坊去中心化和利润之间的平衡。文章还涉及拍卖策略、收益等多方面内容,并通过具体的数学构造进行了严谨的理论推导。
注意:非常感谢 Barnabé Monnot 的审阅、指导和反馈。
引言
以太坊转向基于权益证明(PoS)的共识机制,通过提议者-构建者分离(PBS)^1 在区块提议和构建中引入了明确的角色分工。这种结构不仅提高了操作效率,还为提议者和构建者之间复杂的经济互动奠定了基础。这些互动的核心是由 MEV-Boost 启用的基于拍卖的系统,在这一生态系统中扮演着关键角色。
动机
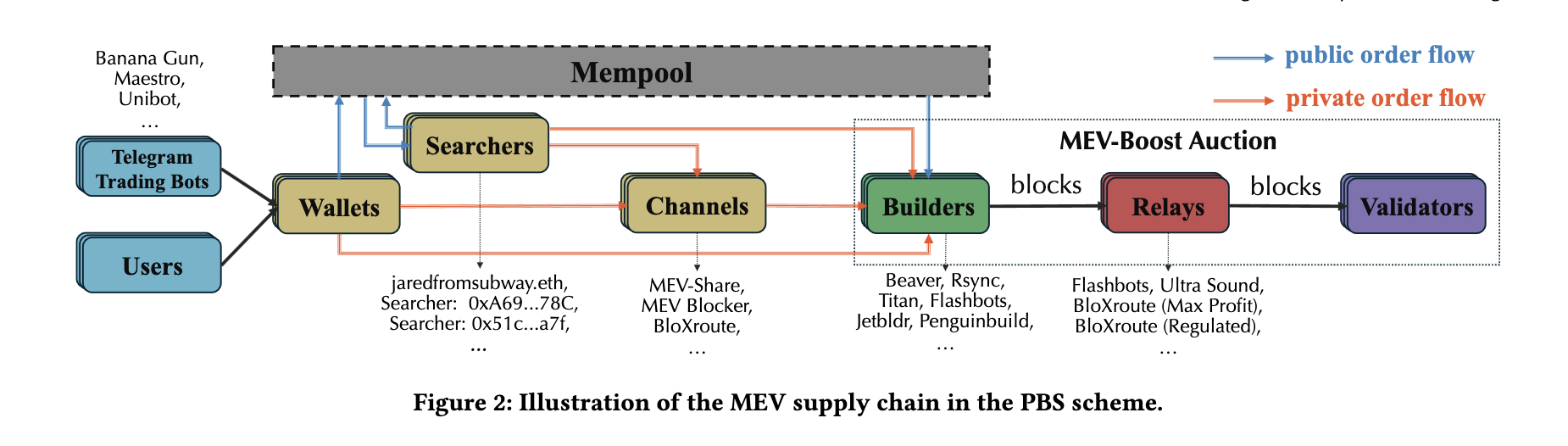
图:PBS 中的 MEV 供应链。Sen Yang 提供,arXiv:2405.01329 [cs.CR]
理解最大可提取价值(MEV)及其在以太坊中的分配对于掌握激励提议者和构建者的经济动机至关重要。最近的数据显示,绕过公共内存池直接发送给构建者的私人订单流——现在影响超过每日区块的 60% ^3。这些私人交易是构建者的重要收入来源和竞争战场。
当前的 MEV-Boost 设置虽然在多个方面有益,但往往有利于已有的构建者,可能导致三明治攻击和中心化等有害行为。这种情况造成了一个信任问题普遍存在的市场,新进入者因需要信誉和高昂的市场准入成本而受到抑制。这种状况威胁到以太坊网络的去中心化性质。
值得注意的是,有积极的提案旨在将以太坊协议内的 PBS 形式化(ePBS)^4,并使构建者角色作为验证者被纳入协议机制,这将减少中继器的作用。这些发展可能会显著改变 PBS 的动态,引入新的拍卖机制并改变提议者和构建者之间的互动方式。我们将讨论从协议外 PBS 过渡到协议内 PBS 及其与密封投标拍卖关系的潜在影响。目前,MEV-Boost 在开放竞价一价拍卖机制下运作。
在这篇博客中,我们关注密封投标拍卖机制——第一价格(FPSB)和第二价格(SPSB)如何影响以太坊网络的经济学。我们将检查它们对提议者支付和构建者策略的影响,以及这些拍卖如何被优化以促进公平和效率。通过对这些拍卖类型进行不同估值分布的模拟,我们旨在提供战略调整及其对网络运营和公平性影响的见解。
深刻理解这些机制不仅对积极参与市场的参与者至关重要,也对应不断完善其共识过程的更广泛的以太坊社区有重要意义。这种分析旨在丰富关于以太坊如何在拍卖机制上保持效率、盈利能力和去中心化平衡的讨论。
密封投标拍卖理论基础
第一价格密封投标拍卖 (FPSBA)
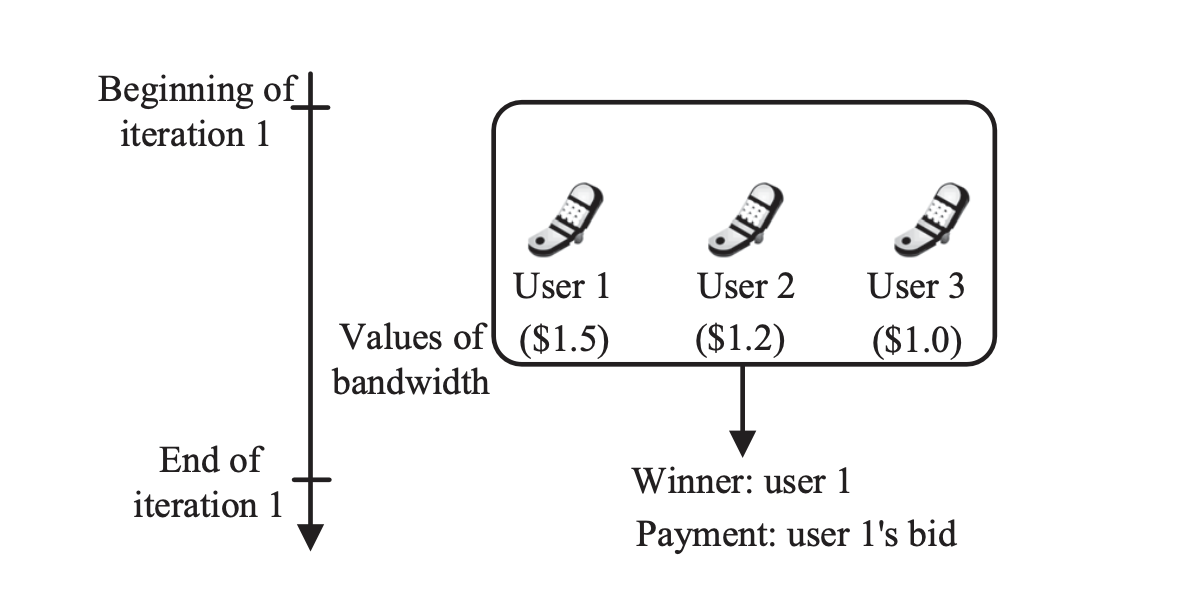 图:带宽资源交易市场的第一价格密封投标拍卖。Niyato D, Luong NC, Wang P, Han Z. 计算机网络的拍卖理论。剑桥大学出版社;2020. 提供
图:带宽资源交易市场的第一价格密封投标拍卖。Niyato D, Luong NC, Wang P, Han Z. 计算机网络的拍卖理论。剑桥大学出版社;2020. 提供
第一价格密封投标拍卖 (FPSBA) 要求每个构建者提交单一的保密投标,不知道其他投标的情况。最高出价者赢得竞标,但必须支付他们准确的出价金额。这种模式鼓励战略性投标,构建者必须仔细平衡其投标金额,以便在不过度付款的情况下获胜。
第二价格密封投标拍卖 (SPSBA)
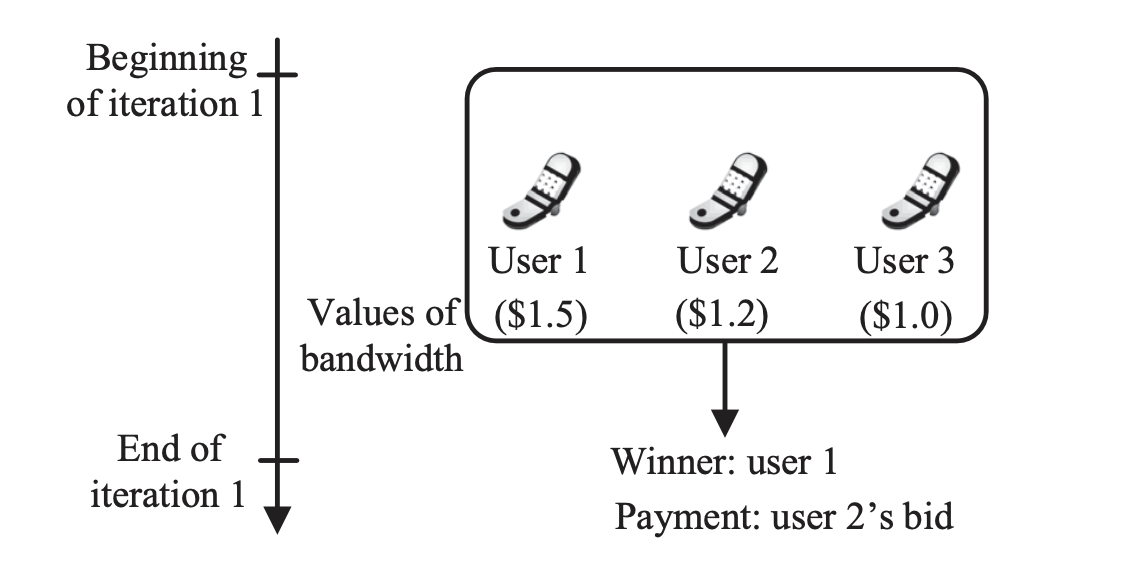 图:带宽资源交易市场的第二价格密封投标拍卖。Niyato D, Luong NC, Wang P, Han Z. 计算机网络的拍卖理论。剑桥大学出版社;2020. 提供
图:带宽资源交易市场的第二价格密封投标拍卖。Niyato D, Luong NC, Wang P, Han Z. 计算机网络的拍卖理论。剑桥大学出版社;2020. 提供
相反,第二价格密封投标拍卖 (SPSBA) 通常称为维克里拍卖,涉及构建者提交单一的隐藏投标。然而,与 FPSBA 不同,最高出价者赢得竞标,但支付第二高出价的金额。这种设置理论上鼓励投标人根据他们的实际估值进行投标,因为获胜价格取决于次高出价,而不是自己的出价,从而减轻过度付款的风险。
构建者估价的分布模型
为了准确模拟这些拍卖,我们使用两种主要的分布模型来表示构建者对区块提案的估值:均匀分布 和 卡方分布。在拍卖模拟中选择这些分布模型对于理解和预测不同拍卖框架内的投标者行为起着重要作用。具体而言,这两种分布提供了建模以太坊拍卖机制中各种现实场景的不同视角。
均匀分布
均匀分布 主要由于其简单性和对信息访问均等假设的符合常被用于模拟。它假定所有结果(在这种情况下是对块的估值)的可能性相等。该模型在以下情景中尤其有效:
- 平等的信息和机会:构建者拥有相同的访问信息的能力和类似交易处理或区块组装能力。这一假设使得所有构建者站在同一水平线上,合理的预计不会有任何单一构建者长时间内持续估值高于或低于其他构建者。
- 简洁的比较基线:它提供了一个清晰、简单的基准,从中可以测量和理解更复杂模型中的变量变化。通过从均匀分布假设开始,更容易在更详细的模拟中逐一隔离每个变量变化的效果。
卡方分布
另一方面,卡方分布 用于代表构建者估值变异性较大和偏斜较为明显的情景。该模型特别适用于以下情况:
- 私有订单流程和信息不对称:一些构建者可能有访问专有算法、内部消息或更快计算资源的优势,使其能够比竞争对手更准确或更激进地评估某些区块的价值。卡方分布因其不对称性和长尾特性有效地营造高变异性及极端值潜力的环境。
- 风险容忍度和投标积极性:具有不同风险容忍度或战略优先级的构建者可能会对赢得区块的潜在回报有不同的评价。那些有私有订单流程或独特策略的人可能会对某些区块给出更高的估值,反映他们预期的额外利润。
为什么这些模型重要
- 分析拍卖动态:通过使用这两个分布模型,我们可以模拟和分析不同类型的构建者在不同的拍卖形式下的行为。这有助于不仅了解平均结果,而且了解结果的范围和分散性,这对拍卖机制的设计产生影响。
- 对机制设计的影响:理解这些分布模型的意义有助于设计更加稳健的拍卖机制,以适应不同构建者的行为和市场条件。例如,如果市场被估值波动较大的构建者主导(如卡方分布模型所示),拍卖设计可能需要考虑到可能出现极高的或极低的出价,并调整规则或参数以确保公平和效率。
收入等价定理和贝叶斯纳什均衡
收入等价定理 (RET) 是拍卖理论中的基本概念^6,指出在某些条件下(如风险中立的投标人、独立的私人价值和对称的投标人),所有标准拍卖形式将为卖方带来相同的预期收益。在以太坊的背景下,这个定理帮助我们理解不同的拍卖类型在理想条件下可能导致类似的提案人的收益结果。
与 RET 相关,贝叶斯纳什均衡 (BNE) 概念是核心^7。在 BNE 中,每位投标人的策略在对其它投标人策略的认知上最大化其期望效用。在以太坊的密封招标拍卖中,BNE 可以引导建筑商基于对他们估值和拍卖格式的估计来决定出价多少。
FPSBA 中的贝叶斯博弈动态
确定 FPSBA 的最优报价面临重大挑战,因为报价过程是私密的。与英式拍卖中投标人可以通过观察他人的出价顺序来预估他们的估值不同,FPSBA 隐藏了每个投标人的估值和策略。这种情况更接近于荷兰式拍卖,其中参与者在不了解他人决策的情况下也能根据已知的所有用户价值分布制定策略。
FPSBAs 本质上是贝叶斯游戏,这类游戏在不完全信息下进行,每个玩家(投标人)不了解其他玩家的策略和收益。然而,每个投标人都对他人的估值有一定的信念,基于已知的概率分布。在此设定下,用来确定每个玩家最佳响应的纳什均衡就是特定的贝叶斯纳什均衡(BNE)。这种平衡考虑了玩家的战略,即在他们理解他人估值分布的前提下最大化他们的期望效用,即使他们不知道具体的投标金额。
在 FPSBA 中,投标人可能会采用出价阴影,有意降低他们的出价以规避过度出价的风险。这种战略性出价既要在试图赢得拍卖的同时防止不相干的收益率结果。
这一贝叶斯博弈框架解释了为何并在高度不确定性下如何投标人尝试优化其出价。以下是 FPSBA 和 SPSBA 的对比表格,其中 $n$ 名建筑商的估值独立且随机从 $[0,1]$ 中抽取:
| 拍卖 | 一级价格 | 二级价格 |
|---|---|---|
| 中标者 | 最高出价者 | 最高出价者 |
| 中标支付 | 中标者的出价 | 第二高出价 |
| 未中标支付 | 0 | 0 |
| 主导策略 | 没有主导策略 | 真实出价是主导策略 |
| 贝叶斯纳什均衡 | 投标人 $i$ 出价 $\frac{n - 1}{n} v_i$ | 投标人 $i$ 真实出价 $v_i$ |
| 卖方收入 | $\frac{n - 1}{n + 1}$ | $\frac{n - 1}{n + 1}$ |
示例
为了说明封闭投标拍卖中的平衡出价和提案人收入的概念,考虑一个两个建设者各自估算值从区间 $[0,1]$ 独立且均匀抽取的场景。该示例着重展示了不同拍卖格式如何影响提案人的收入:
-
在一阶封闭出价拍卖(FPSBA)中: 每个建设者的平衡出价计算为估值的一半,旨在平衡获胜的潜在成本和区块的价值。如果建筑者的估值分别为 $v_1$ 和 $v_2$,他们的出价将分别是 $\frac{v_1}{2}$ 和 $\frac{v_2}{2}$。提案人获得这两笔出价中较高的出价,即 $\max(\frac{v_1}{2}, \frac{v_2}{2})$。这代表了建筑商愿意支付的最高价格,同时仍然设法最大化他们的回报。
-
在二阶封闭出价拍卖(SPSBA)中: 建筑者们出价他们的真实估值 $v_1$ 和 $v_2$,因为中标的建筑者支付的是次高出价,这也激励他们诚实地出价,而不必担心会超付。在这种情况下,提案人收到次高出价,也就是 $\min(v_1, v_2)$。
在这两种拍卖类型中,有趣的结果是,在这些出价策略和估值假设下计算的提案人的预期收入都等于 $1/3$。这种收入在两种拍卖类型中的等效性展示了经济学理论中的收入等值原则,在理想的条件下,理性的投标者和特定的估值分布和投标者风险行为假设下,拍卖格式不影响卖家的平均收入。
模拟设定
Python 模拟环境
对于我们的 FPSBA 和 SPSBA 模拟,我们建立了一个 Python 模拟环境。我们使用了 NumPy、Pandas、Matplotlib、Plotly 和 SciPy 库来准确分析和可视化拍卖动态。
你可以在这里找到 python jupyter notebook 这里,完整的代码可在 GitHub repo 找到 这里。
模拟参数
我们选择的模拟参数旨在探索不同拍卖机制在控制情形下单矛盾的竞争场景中对提案者收入和投标人策略的影响:
-
投标人数量 (N): 我们模拟的拍卖场景包含 10 个投标人。这个数量确保了拍卖环境具有足够的竞争力,以模拟实际世界中的投标竞争,从而洞悉投标人的行为和拍卖结果。
-
分布类型:
- 均匀分布: 在这种分布下,投标人的估值均匀分布在 $[0,1]$ 范围内,反映了所有可能估值均等概率出现的情形。此分布作为一个基准,用来评估相对简单情境下的投标人策略。
- 卡方分布: 这种分布被选用于模型更具偏态估值的情境,可能反映了投标人可能具有不对称信息的情况,特别是来自私人订单流时。它帮助我们研究具有不同程度信息的投标人在拍卖中的表现。
-
拍卖机制:
- FPSBA: 在这种机制中,投标人提交密封投标,最高投标人胜出,但要支付他们恰好所投的数量。重点在于了解投标人如何根据他们手头的信息,在不超额支付的情况下制定策略以赢得拍卖。
- SPSBA: 投标人同样提交密封投标;但是,最高投标人支付第二高投标金额。这种机制测试了投标的诚实性以及对其他投标人预期行为的策略反应。
-
采样数 (R): 为了确保结果的鲁棒性,每组模拟多次运行,具体来说进行了 $R$ 次抽取,其中 $R$ 是一个足够大的数,以允许统计上显著的结果。这种复制有助于在不同模拟运行中评估拍卖结果的变异性和可靠性。
收益递减原理和 FPSBA 中赢取投标的估计方法
收益递减原理 (RET) 表明,在某些标准条件下——风险中立的投标人、独立的估值和对称的投标人——不同的拍卖类型会产生相同的预期卖家收益,尽管投标策略和支付规则各异^6。该原理凸显了当从拍卖师的视角来看时传统拍卖形式在经济发展中的根本相似之处。
在实践中,尤其是在 FPSBA 的上下文中,确定最佳投标涉及复杂的策略计算,尤其是在面对其他投标人估值不完全信息时。为了近似某一已知估值 $v_i$ 的最佳投注,在假设其他所有投标人的估值都小于 $v_i$ 的情况下,我们可以采用系统的方法来估计第二高投标,这是设定 FPSBA 中最终定价的重要因素。
第二高价估计方法
我们的计算程序如下所述:
- 输入参数:
- $\bar{v}$: 最低截断值,代表已知最高投标估值小于 $v_i$。
- $R$: 模拟抽样次数,决定了我们估算的稳健性。
- 模拟抽取:
- 生成 $v_r$ 投标估值,$r = 1, \ldots, R$,其中每个 $v_r$ 是从假设分布中抽取的模拟估值。
- 子集与重组:
- 识别满足 $\mathcal{R}$ = $r \in$ { $1, \ldots, R$ } $\vert v_r \leq \bar{v}$ 的子集 $\mathcal{R}$,仅包括那些估值小于或等于 $\bar{v}$ 的抽取。
- 重新安排数据集,令其转换为 $v_{i,r}$,其中 $i = 1, \ldots, N$ 且 $r = 1, \ldots, \tilde{R}$,通过丢弃最后 $\text{mod}(\vert \mathcalR \vert, N)$ 观测值来调整数据维度,确保分析所需的平衡矩阵。
- 计算第二大值:
- 对于每个满足 $\mathcalR$ 内的模拟结果 $r$,确定第二大值 $v_{(n-1),r}$,这表示在 $v_i$ 成为最高投标的情况下次高投标。
- 估计期望值:
- 计算预期值 $\hat{\mathbb{E}}(v{(n-1)})$ 为 $R^{-1} \sum{r=1}^R v_{(n-1),r}$,从而提供所有有效模拟中次高投标的平均值。
这种方法提供了一种统计学上稳健的方式,来近似 FPSBA 中的预期次高投标,让投标者能够策略性地将其出价略微放大方略,以最大限度增加以最小附加成本获胜的机会。这样的计算对于部署有效的出价策略至密封出价框架至关重要,强调了轻松驾驭如此复杂的拍卖系统的必要分析深度。
以下是如何通过参考的曲线看出截取后的均匀分布和卡方分布的图示:
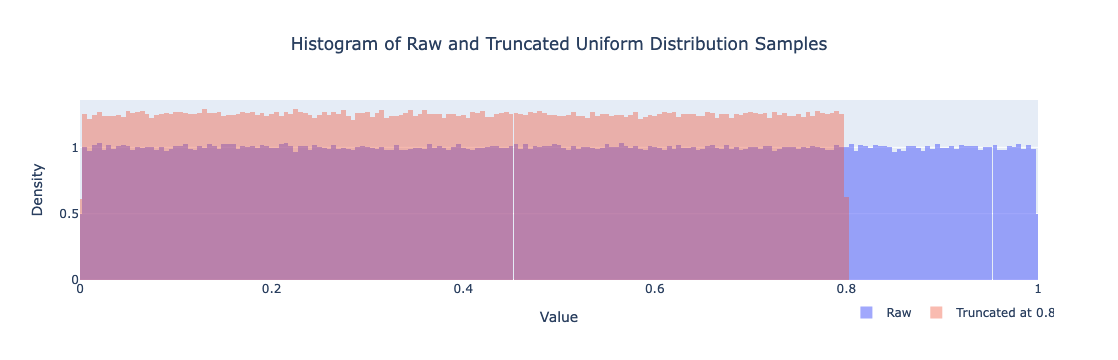
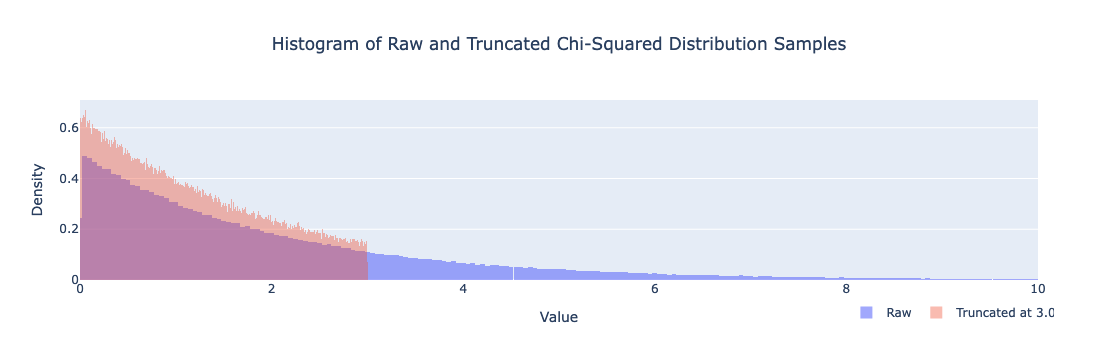
卡方分布下的 FPSBA 投标策略
- 抽样: 首先从卡方分布中生成大量估值样本。这些样本代表其他投标者对你正在考虑的同一区块可能赋值的估值。
- 截取: 对于你的最大投标考量 $v_i$, 截断所有抽样的估值在这个值之下。此步骤模拟了你假设没有其他投标者会出价超过你的最大愿意支付的场景 $v_i$。这个截取很重要,因为它限制了你考虑的投标范围在不超过 $v_i$,反映了一种保守但战略性避免过高投标的方法。
- 计算最大值: 在每次截断后形成的一个子集中,找出 $N-1$ 投标者的最高估值。如果 $v_i$ 是赢家,那么这个数值代表在 FPSBA 场景下的最优出价,因为它是对赢得拍卖所需的最大招投标金额,给定 $N-1$ 失败者竞标。
- 期望值计算: 计算这些最高值在所有子集中的平均值。这个期望最优出价 $\hat{\mathbb{E}}(v_{(n-1)})$ ,作为你估值是在 $v_i 。
## 条件 $v_i$ 是赢家时的期望值;
## 计算从截断分布中获取最大值的期望值,在 N-1 投标者的情况中
Ev = np.empty(vgrid.shape)
for i,this_v in enumerate(vgrid):
Ev[i] = Ev_largest(this_v, v, N-1)def Ev_largest(vi, v_sim_untruncated, N, R_used_min=42):
'''Ev_largest:compute the expected value of maximum drawing from a truncated distribution
where v_sim_untruncated are draws from the untruncated and vi is the
truncation point.
INPUTS:
vi: (scalar) upper truncation point
v_sim_untruncated: (R-length 1-dim np array) draws of v from the untruncated distribution
N: (int) number of draws per iteration
R_used_min: (int, optional) assert that we have at least this many samples. (Set =0 to disable.)
OUTPUTS
Ev: (float) expected value of the largest across simulations
R_used: (int) no. replications used to compute simulated expectation
'''
assert v_sim_untruncated.ndim == 1, f'Expected 1-dimensional array'
# 进行截断
I = v_sim_untruncated <= vi
v_sim = np.copy(v_sim_untruncated[I])
# 丢弃额外行
drop_this_many = np.mod(v_sim.size, N)
if drop_this_many>0:
v_sim = v_sim[:-drop_this_many]
# 重塑
R_used = int(v_sim.size / N)
v_sim = np.reshape(v_sim, (N,R_used))
assert R_used > R_used_min, f'Too few replications included: only {R_used}. Try increasing original R.'
# 找到最大值
v_sim = np.sort(v_sim, 0) # 排序上升 ...
v_largest = v_sim[-1, :] # ... 所以最后一 *行* 是列(样本)中的最大值
# 评估期望值
Ev = np.mean(v_largest)
return Ev结果与分析
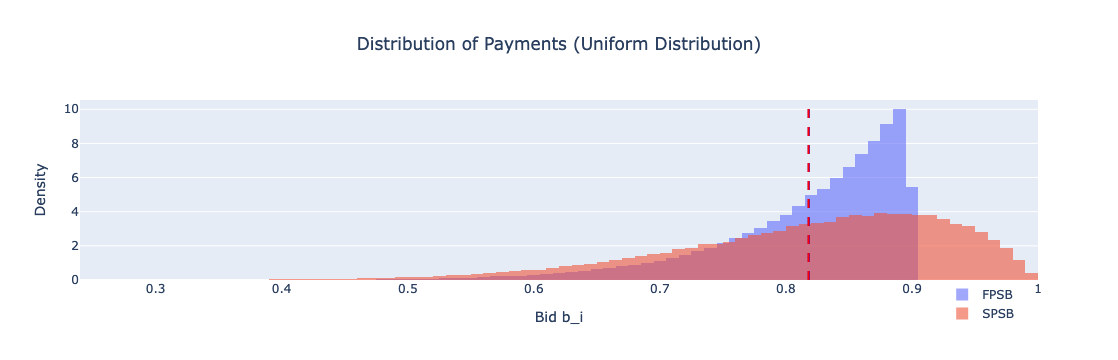 图:支付分布(统一分布)
图:支付分布(统一分布)
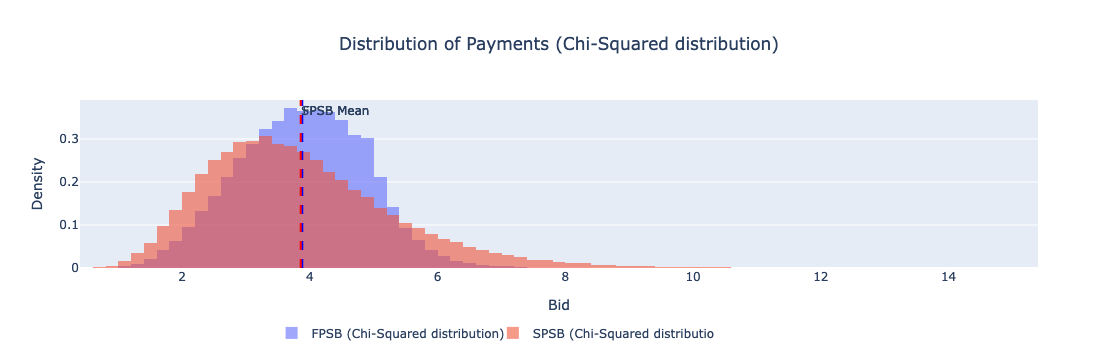 图:支付分布(卡方分布)
图:支付分布(卡方分布)
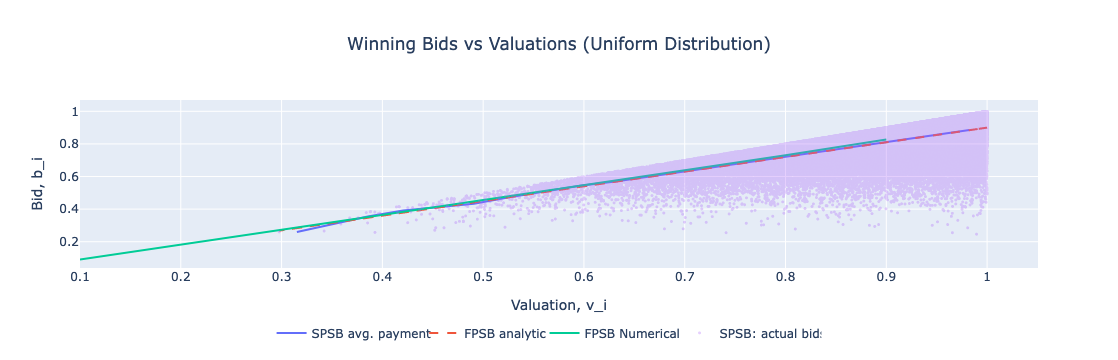 图:赢取出价 vs 估价(统一分布)
图:赢取出价 vs 估价(统一分布)
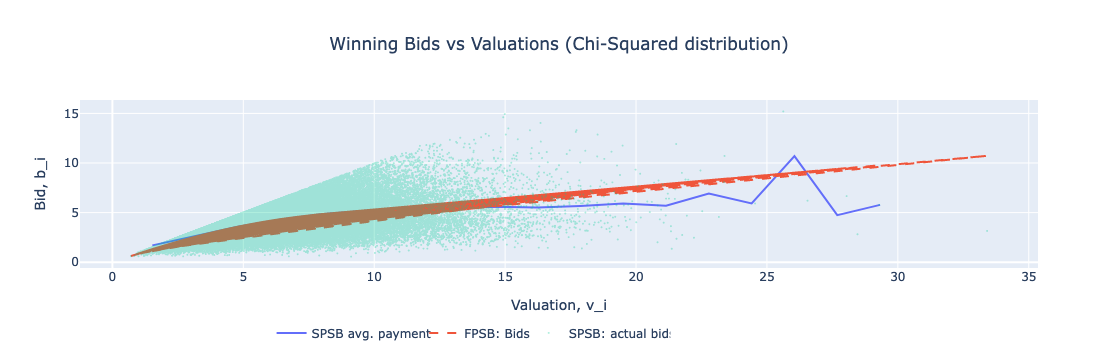 图:赢取出价 vs 估价(卡方分布)
图:赢取出价 vs 估价(卡方分布)
这里是一个总结了在统一和卡方分布下两种拍卖类型各自的平均支付和相应标准差的表格。
| 分布 | 拍卖 | 均值 | 标准差 |
|---|---|---|---|
| 统一分部 | FPSB | 0.81817 | 0.07 |
| 统一分部 | SPSB | 0.81795 | 0.11 |
| 卡方分布 | FPSB | 3.88028 | 1.00 |
| 卡方分布 | SPSB | 3.85591 | 1.48 |
统一分部
- FPSBA 对比 SPSBA:在统一分布下,FPSBA 和 SPSBA 显示出非常相似的平均支付,FPSBA 平均支付为 0.81817,标准差为 0.07,而 SPSBA 平均支付为 0.81795,标准差较高为 0.11。接近的平均值表明,在统一分布条件下,收益等价定理成立,因为这两种拍卖类型几乎为提议者提供了相同的收益。然而,SPSBA 较高的标准差表明出价有更大的变化(尤其是在高估值端),可能是由于投标人更有信心出价接近其真实估值,知道他们只需支付次高出价。
卡方分布
- FPSBA 对比 SPSBA:在卡方分布场景中,FPSBA 的平均支付约为 3.88028,标准差为 1.00,而 SPSBA 的平均支付为 3.85591,标准差为 1.48。这表明收益等价定理成立,SPSBA 因其支付机制倾向于鼓励更激进的出价。在卡方分布下,SPSBA 较高的标准差证实了这种拍卖类型可能导致范围更广的出金额,反映了被拍卖区块的感知价值更大范围。
对提议者收入最大化的含义
-
SPSBA 的潜在优势:尽管在平均收益方面两种拍卖类型的表现大体相似,SPSBA 在出价上有更高的差异可能对提议者有利,特别是在投标人对区块有高估价的情形下。由于 SPSBA 鼓励投标人出价其真实估值,可能导致比 FPSBA 更高的支付,因为投标人可能会低估他们的真实估值。
-
投标人策略考虑:分析显示,SPSBA 投标人更有可能激进出价,这可能导致偶发的提议人收入飙升,特别是在卡方分布下。相比之下,FPSBA 投标人可能会采用出价阴影来规避过度支付的风险,导致更一致但潜在更低的支付给提议人。
可视化和战略启示
提供的可视化结果强调了这些观点,展示了支付的分布和两类拍卖中出价的差异。图表突出了 FPSBA 中的出价阴影如何导致较低的出价集中在较低值之间,而 SPSBA 中的出价则更为分散。这一分析不仅有助于理解不同类型拍卖的战略依据,也有助于提议者和投标人制定最大化各自回报的策略,以在以太坊的拍卖为基础的 PBS 系统中操作。
FPSBA 模拟的结果
FPSBA 的模拟结果提供了有关投标行为及其对提议者财务影响的有用数据:
-
出价和支付的分布:无论是均匀分布还是卡方分布,FPBA都表现出投标人的估价和出价之间的显著相关性,这些出价大约是估价的一半,这是由于采用了出价阴影策略。这种关系在显示FPSBA出价作为估价百分比的图表中很明显,突显了估价增加时出价百分比在卡方分布中下降的趋势。
-
平均值和支付的方差:在均匀分布中,FPSBA的平均支付约是0.81817,标准差为0.07。在卡方分布中,平均支付大幅增加到3.88028,具有更高的1.00标准差,表明支付的可变性更大。这一增长表明,当估值广泛变化时(如卡方分布所模拟的那样),竞争和投标金额都会增加,可能提高提议者的收入。
SPSBA 模拟的见解
第二次密封出价拍卖(SPSBA)提供了一种投标行为和结果的对比:
-
与FPSBA的比较:在均匀分布情景下,FPSBA与SPSBA之间的平均支付几乎相同,表明在这些条件下收入等价定理的有效性。然而,SPSBA在支付方面显示出更高的方差,标准差在均匀分布为0.11,卡方分布为1.48,这表明投标人倾向于出价接近其真实估值,导致了赢家出价范围更广。
-
SPSBA优于FPSBA的情况:在由卡方分布模拟的情景中,价值评估高度不同时,SPSBA在最大化提议者收入方面可能优于FPSBA。这是因为SPSBA的主导策略是如实出价,这往往会提高第二高出价,尤其是当投标人的估值较高时。与FPSBA相比,在SPSBA下投标人不用担心过度支付,因此会更积极地进行接近真实估值的出价。
出价阴影的可视化及其意义
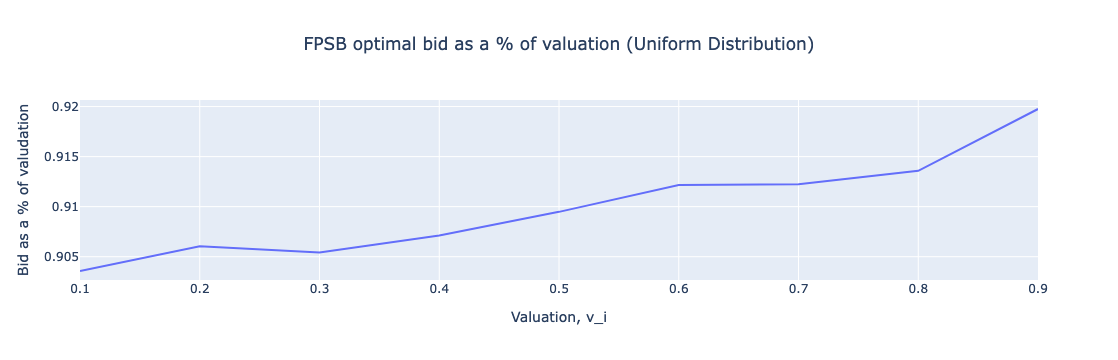 图:FPSB最优出价占估值百分比(均匀分布)
图:FPSB最优出价占估值百分比(均匀分布)
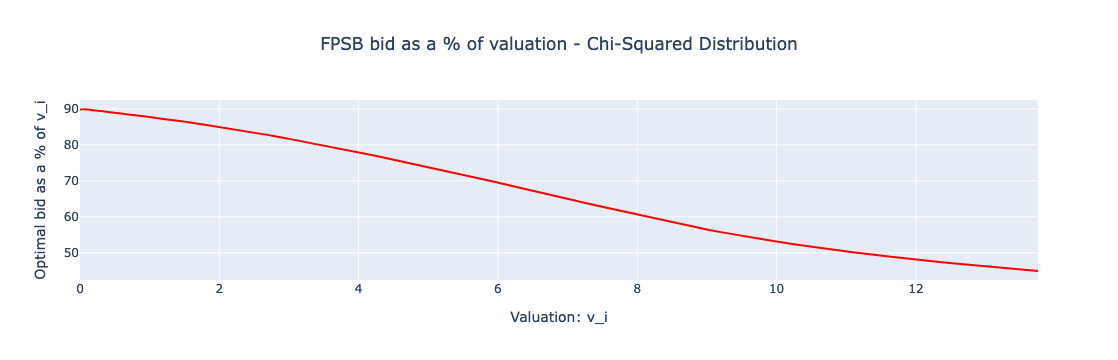 图:FPSB最优出价占估值百分比(卡方分布)
图:FPSB最优出价占估值百分比(卡方分布)
可视化清楚地展示了出价阴影如何影响拍卖结果。在FPSBA中,投标人倾向于降低其出价作为一种避免过度支付的策略,这从最优出价作为估值百分比的图表中可以看出。这种策略导致出价集中于较低值附近,这与SPSBA相比,受投标人对自己的估值准确性充满信心的情况下,出价可能会更高或更低。
总体而言,这些结果突出了拍卖机制的细微差别及其对投标人行为和提议者收入的影响。虽然FPSBA可能会导致更加谨慎的出价,但SPSBA促进了更多样化的出价范围,每一个出价都紧密反映投标人的真正估值,从而在估值变动性高的情况下,可能会提升提议者的收入。这种分析不仅有助于理解不同类型拍卖的战略依据,也有助于在以太坊的拍卖为基础的PBS系统中拟定指南,帮助提议者最大化他们的收入。
实际意义
对构建者和提议者的策略影响
从这些密封投标拍卖模拟中得出的见解为以太坊 PBS 系统中的构建者和提议者提供了一个战略蓝图。构建者可以根据密封投标拍卖类型改进其投标策略;例如,在 SPSBA 情景中,接近真实估值出价可能是有利的,因为次高投标定价机制可能会带来更高的提议者收入,且无过度支付风险。而对于 FPSBA,则有必要实施更保守的出价阴影策略以避免过度支付,尤其是在高变异性估值环境中。
另一方面,提议者可以利用这些见解更好地预测不同拍卖格式的结果,基于预期收入和愿意接受的投标变化,影响他们在 FPSBA 和 SPSBA 之间的选择。理解这些动态对于在维持公平竞争的投标环境的同时最大化收入至关重要。
提高拍卖效率和公平性
为了提高区块提议的效率和公平性,可以引入调整策略,比如调整投标人之间的信息对称性,或修改拍卖规则,以尽量减少诸如非常低或非常高的投标这些不反映区块真实价值的极端结果。这些调整可以帮助稳定投标环境,确保提议者收入更具可预测性。
对协议开发的影响
这些模拟的结果对未来协议开发有更广泛的含义,特别是微调 PBS 机制。随着以太坊的不断演进,整合这些发现可能会导致更强大的拍卖机制设计,可能结合 FPSBA 和 SPSBA 元素的混合模式,以在网络中更有效地平衡风险和奖励。
未来研究方向
展望未来,进一步的研究可以深入探讨混合拍卖机制,建造者和/或提议者欺骗行为的影响,或者建造者的时间游戏,或多阶段或多重轮投标,其中一个插槽拍卖内可以由建造者提交多次投标,或提议者泄露某建造者的投标或取消动态,或者引入适应即时反馈的动态投标策略。调查这些领域可以提供更细粒度的见解,以优化以太坊的 PBS 机制,以实现更好的扩展性和安全性。
行动号召
我们鼓励以太坊社区的开发者和研究人员参与本研究所使用的模拟代码,以进一步探索这些发现。你的反馈和见解对于完善和推进这项研究非常宝贵。如果你有兴趣实验模拟或有改进建议,请访问我们的 GitHub 仓库 此处 下载代码并参与以太坊拍卖机制的持续开发。
你的参与和反馈对于推动创新和确保以太坊继续演进至关重要。让我们合作增强并优化这些系统,以为去中心化以太坊的未来服务。
##!/usr/bin/env python
## coding: utf-8
## # 以太坊协议内外的首次密封价格投标与第二次密封价格投标
import numpy as np
import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
from scipy import stats
from scipy import interpolate
## 确保本笔记本生成相同答案
np.random.seed(1337)
## ## 收益等值定理
##
## 根据收益等值定理,卖方(提案者)在第一或第二次密封价格投标拍卖中的预期收益是相同的。
##
## 在 FPSB 和 SPSB 中的平均支付将是相同的,但我们感兴趣的是研究支付的分布以及针对估价的投标策略。这可以帮助我们在已知区块价值的基础上展示如何定价。
## ## 第二排序统计量的期望
##
## 我们的流程如下:
##
## * 输入: $\bar{v}$: 下限截断值, $R$: 抽取次数。
## 1. 已抽取 $v_{r}$ for $r = 1,...,R$.
## 2. 子集,选择 $\mathcal{R} \equiv \{ r \in \{1,...,R\} \vert v_{r} \le \bar{v} \}$
## 3. 重构成 $v_{i,r}$ for $i = 1,...,N$ 和 $r = 1,..., \tilde{R}$.
## * 注意:我们需要扔掉一些最后的观测值,以保证有正方形矩阵。具体而言,我们会扔掉最后一个 mod$(\vert \mathcal{R} \vert, N)$ 抽样。
## 4. 对每次模拟 $r \in \mathcal{R}$,找到第二大的值,$v_{(n-1),r}$
## 5. 返回 $\hat{\mathbb{E}}(v_{(n-1)}) = R^{-1} \sum_{r=1}^R v_{(n-1),r}$.
## In[2]:
def Ev_largest(vi, v_sim_untruncated, N, R_used_min=42):
'''Ev_largest: 计算从截断分布中绘制出来的最大值的期望值
v_sim_untruncated是从未截断分布抽取的样本,vi是截断点
输入:
vi: (标量)上限截断点
v_sim_untruncated: (R长度的一维np数组) 来自未截断分布的v抽样
N: (整数)每次迭代的抽样数
R_used_min: (整数,可选)确保至少有这个数量的样本。(设为0禁用)
输出
Ev: (浮点数) 最大值跨模拟的期望值
R_used: (整数) 用于计算模拟期望的重复次数
'''
assert v_sim_untruncated.ndim == 1, f'期望一维数组'
# 执行截断
I = v_sim_untruncated <= vi
v_sim = np.copy(v_sim_untruncated[I])
# 删除多余的行
drop_this_many = np.mod(v_sim.size, N)
if drop_this_many>0:
v_sim = v_sim[:-drop_this_many]
# 重构
R_used = int(v_sim.size / N)
v_sim = np.reshape(v_sim, (N,R_used))
assert R_used > R_used_min, f'包含重复项太少:只有 {R_used} 个。尝试增加初始R.'
# 找到最大值
v_sim = np.sort(v_sim, 0) # 降序排序 ...
v_largest = v_sim[-1, :] # ... 所以最后一 *行* 是最大值所在列(样本)
# 评估期望值
Ev = np.mean(v_largest)
return Ev
N = 10
R = 100000
## ## 均匀分布模拟
np.random.seed(1337)
## 为建设者生成随机估值
v = np.random.uniform(0,1,(N,R))
## 贝叶斯纳什均衡 (BNE) 在一次封装密封投标中
b_star = lambda vi,N: (N-1)/N * vi
b = b_star(v,N)
## ### 获取最高和次高投标
## 排序和索引
idx = np.argsort(v, axis=0)
v = np.take_along_axis(v, idx, axis=0)
b = np.take_along_axis(b, idx, axis=0)
ii = np.repeat(np.arange(1,N+1)[:,None], R, axis=1)
ii = np.take_along_axis(ii, idx, axis=0)
winning_player = ii[-1,:]
winner_pays_fpsb = b[-1, :] # 最高出价
winner_pays_spsb = v[-2, :] # 次高估值
## ### 支付分布(均匀分布)
##
## 我们从**收益等价定理**知道,*平均*支付应该是相同的。然而,支付的分布*看起来*可能不同。也就是说,获胜支付的方差、中位数等可能不同。## 绘制付款分布(均匀分布)
fig = make_subplots(rows=1, cols=1)
for x, lab in zip([winner_pays_fpsb, winner_pays_spsb], ['FPSB', 'SPSB']):
print(f'平均支付 {lab} (均匀分布): {x.mean(): 8.5f} (标准差 = {np.sqrt(x.var()): 5.2f})')
fig.add_trace(go.Histogram(x=x, histnorm='probability density', name=lab, nbinsx=100), row=1, col=1)
## 添加均值竖线
fig.add_vline(x=winner_pays_fpsb.mean(), line_width=2, line_dash="dash", line_color="blue")
fig.add_vline(x=winner_pays_spsb.mean(), line_width=2, line_dash="dash", line_color="red")
fig.update_layout(title_text='付款分布(均匀分布)', xaxis_title='出价 b_i', yaxis_title='密度', barmode='overlay', title_x=0.5, legend=dict(yanchor="top",y=0,xanchor="left",x=0.9))
fig.update_traces(opacity=0.6)
fig.show()
## 接下来我们绘制**获胜出价**$b_{(n)}$(即付款)相对于估值$v_{(n)}$的对比图,分别针对 FPSB 和 SPSB。这里可能会注意到:
## * FPSB:每个估值对应唯一的出价,
## * SPSB:即使固定获胜者的估值,获胜者支付也有所不同(等于次高类型的估值)。
## 绘制获胜出价与估值的关系图
binned = stats.binned_statistic(v[-1, :], v[-2, :], statistic='mean', bins=20)
xx = binned.bin_edges
xx = [(xx[i]+xx[i+1])/2 for i in range(len(xx)-1)]
yy = binned.statistic
v = v.flatten()
vgrid = np.linspace(0, 1, 10, endpoint=False)[1:]
Ev = np.empty((vgrid.size,))
bds = np.empty((vgrid.size,))
t_v = np.empty((vgrid.size,))
for i,this_v in enumerate(vgrid):
Ev[i] = Ev_largest(this_v, v, N-1)
bds[i] = Ev[i]/this_v
t_v[i] = this_v
v = v.reshape((N,R))
## 绘制获胜出价与估值的关系图(均匀分布)
fig = go.Figure()
fig.add_trace(go.Scatter(x=xx, y=yy, mode='lines', name='SPSB 平均支付'))
fig.add_trace(go.Scatter(x=v[-1, :], y=b[-1, :], mode='lines', name='FPSB 解析解', line=dict(dash='dash')))
fig.add_trace(go.Scatter(x=vgrid, y=Ev, mode='lines', name='FPSB 数值解'))
fig.add_trace(go.Scatter(x=v[-1, :], y=v[-2, :], mode='markers', name='SPSB: 实际出价', opacity=0.3, marker=dict(size=3)))
fig.update_layout(title='获胜出价与估值的对比(均匀分布)', xaxis_title='估值, v_i', yaxis_title='出价, b_i', title_x=0.5, legend=dict(yanchor="top",y=-0.3,xanchor="left",x=0.2, orientation="h"))
fig.show()
## 绘制出价调整为价值的比例
fig = go.Figure()
fig.add_trace(go.Scatter(x=t_v, y=bds, mode='lines', name='FPSB 出价调整'))
fig.update_layout(title='作为估值比例的FPSB最优出价(均匀分布)', xaxis_title='估值, v_i', yaxis_title='最优出价占估值的比例', title_x=0.5)
fig.show()
## ## $\chi^2$ 分布模拟
## 在 FPSB 中由于没有解析解,因此求解最优出价难度较高。我们将通过数值模拟近似计算。
np.random.seed(1337)
v = np.random.chisquare(df=2, size=(N*R,))
## 生成估值
np.random.seed(1337)
v = np.random.chisquare(df=2, size=(N*R,))
## 生成网格
ngrid = 100
pcts = np.linspace(0, 100, ngrid, endpoint=False)[1:]
vgrid = np.percentile(v, q=pcts)
## 预期在条件 $v_i$ 为获胜者下的最大值;
## 计算从一个截断分布中抽取的最大值的期望值,在这个截断分布中有n-1个投标者
Ev = np.empty(vgrid.shape)
for i,this_v in enumerate(vgrid):
Ev[i] = Ev_largest(this_v, v, N-1)
## 按照构造/假设,估值最低的投标人始终支付零
Ev = np.insert(Ev, 0, 0.0)
vgrid = np.insert(vgrid, 0, 0)
## 设置插值函数用于求解
b_star_num = interpolate.interp1d(vgrid, Ev, fill_value='extrapolate')
## 创建更精细的网格进行插值
pcts = np.linspace(0, 100, 1000, endpoint=False)
vgrid_fine = np.percentile(v, q=pcts)
## 绘制 FPSB 的最优出价
fig = go.Figure()
fig.add_trace(go.Scatter(x=vgrid, y=Ev, mode='markers', marker=dict(color='red', symbol='circle'), name='网格上的解'))
fig.add_trace(go.Scatter(x=vgrid_fine, y=b_star_num(vgrid_fine), mode='lines', name='插值解'))
fig.update_layout(title='FPSB - 卡方分布的最优出价', xaxis=dict(title='估值: v_i'), yaxis=dict(title='在 FPSB 中的最优出价: E(v_{(n-1)} | v{(n)} = v)'),legend=dict(x=0.8, y=0.1),title_x = 0.5)
fig.show()
## 调整 v 的形状
v = v.reshape((N,R))
b = b_star_num(v)
## 计算 FPSB 和 SPSB 的胜者支付
idx = np.argsort(v, axis=0)
v = np.take_along_axis(v, idx, axis=0) # 与 np.sort(v, axis=0) 相同,除了我们现在保留 idx
b = np.take_along_axis(b, idx, axis=0)
ii = np.repeat(np.arange(1,N+1)[:,None], R, axis=1)
ii = np.take_along_axis(ii, idx, axis=0)
winning_player = ii[-1,:]
winner_pays_fpsb = b[-1, :] # 最高出价
winner_pays_spsb = v[-2, :] # 次高估值
## 绘制付款分布
fig = make_subplots(rows=1, cols=1)
for x, lab in zip([winner_pays_fpsb, winner_pays_spsb], ['FPSB', 'SPSB']):
print(f'卡方分布下的平均支付 {lab}: {x.mean(): 8.5f} (标准差 = {np.sqrt(x.var()): 5.2f})')
fig.add_trace(go.Histogram(x=x, histnorm='probability density', name=f'{lab} (卡方分布)', nbinsx=100), row=1, col=1)
fig.add_vline(x=winner_pays_fpsb.mean(), line_width=2, line_dash="dash", line_color="blue", annotation_text="FPSB 均值")
fig.add_vline(x=winner_pays_spsb.mean(), line_width=2, line_dash="dash", line_color="red", annotation_text="SPSB 均值")
fig.update_layout(title_text=f'付款分布(卡方分布)', xaxis_title='出价', yaxis_title='密度', barmode='overlay', title_x = 0.5, legend=dict(yanchor="top",y=-0.3,xanchor="left",x=0.2, orientation="h"))
fig.update_traces(opacity=0.6)
fig.show()
binned = stats.binned_statistic(v[-1, :], v[-2, :], statistic='mean', bins=20)
xx = binned.bin_edges
xx = [(xx[i]+xx[i+1])/2 for i in range(len(xx)-1)]
yy = binned.statistic
## 绘制获胜出价与估值的关系图
fig = go.Figure()
fig.add_trace(go.Scatter(x=xx, y=yy, mode='lines', name=f'SPSB 平均支付'))
fig.add_trace(go.Scatter(x=v[-1, :], y=b[-1, :], mode='lines', name=f'FPSB: 出价', line=dict(dash='dash')))
fig.add_trace(go.Scatter(x=v[-1, :], y=v[-2, :], mode='markers', name=f'SPSB: 实际出价', opacity=0.3, marker=dict(size=2)))
fig.update_layout(title=f'获胜出价与估值的对比(卡方分布)', xaxis_title='估值, v_i', yaxis_title='出价, b_i', title_x = 0.5, legend=dict(yanchor="top",y=-0.3,xanchor="left",x=0.2, orientation="h"))
fig.show()
## 绘制出价调整为价值的比例
xx = np.linspace(0.1, 10, 10)
yy = np.array([b_star_num(v)/v*100.0 for v in vgrid_fine])
fig = go.Figure()
fig.add_trace(go.Scatter(x=vgrid_fine, y=yy, marker=dict(color='red', symbol='circle'), name='出价调整'))
fig.update_layout(title='作为估值比例的 FPSB 出价 - 卡方分布', xaxis=dict(title='估值: v_i'), yaxis=dict(title='最优出价占 v_i 的比例'),legend=dict(x=0.8, y=0.1),title_x = 0.5)
fig.show()
参考文献
- 原文链接: github.com/thogiti/thogi...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 意图聚合器比传统交换更流畅吗? - CoW DAO 108 浏览
- 以太坊区块构建管道:去中心化之路 183 浏览
- 区块链中的“黑暗森林”:理解MEV与捕食性动态 – ImmuneBytes 174 浏览
- 什么是DeFi?去中心化金融指南 - CoW DAO 312 浏览
- L1 价值捕获的压缩 256 浏览
- DeFi和加密货币之间有区别吗?——CoW DAO 422 浏览
- 什么是DeFi聚合器?——CoW DAO 258 浏览
- 顶级DeFi交易所:理解去中心化交易基础设施 - CoW DAO 416 浏览
- 如何开始你的第一个 Uniswap V4 Hook:要点、库与风险 12 浏览
- Solana的区块构建之战 344 浏览
- 如何去中心化构建区块? 428 浏览
- CoW DAO月度回顾:2026年1月 - CoW DAO 416 浏览

