深入理解 Uniswap v3 白皮书

深入理解 Uniswap v3 白皮书

概述

Uniswap v3是一个基于以太坊虚拟机（EVM）实现的无监管自动做市商（AMM）。与之前的版本相比，Uniswap v3提高了资金利用率，赋予流动性提供者更多控制能力，改进了价格预言机的准确性和便利性，同时增加了更灵活的手续费结构。

1 Introduction 介绍

自动做市商（AMMs）是集中流动性，并基于算法将其开放给交易者的代理商。常值函数做市商（CFMMs）（Uniswap也是成员之一）作为AMM中的一个常见类别，已被广泛应用于去中心化金融场景，他们一般都在无需许可的区块链上以交易代币的智能合约的形式实现。

当前市场上的常值函数做市商大多存在资金利用率不高的问题。在Uniswap v1/v2使用的恒定乘积做市商公式中，对于给定价格，池子中仅部分资金参与做市。这显得十分低效，特别是当代币总是在特定价格附近交易时。

注：以稳定币为例，USDC/USDT的波动范围极小，而根据v2的公式，流动性提供者实际上会将资金分布在价格区间(0, $\infty$)，即使这些价格几乎永远也无法使用到。因此在Uniswap v1/v2版本，资金利用效率较低，同时也导致交易滑点相对较高。

在此之前，Curve和YieldSpace等一些产品尝试解决这个资金利用率问题，他们通过建立池子，并使用不同的函数描述代币之间的关系。这要求池子里的所有流动性提供者都遵守同一个公式，而如果他们希望在不同的价格区间提供流动性，将导致流动性分裂。

在本文，我们将介绍Uniswap v3，一种新的自动做市商（AMM），它给予流动性提供者对资金被使用的价格区间更多控制权，并降低流动性分裂和gas消耗等问题的影响。该设计不依赖任何基于代币价格行为的共同假设。Uniswap v3仍然基于之前版本的常值函数曲线（即 $x \cdot y = k$），但提供许多重要的新特性：

• 集中流动性：流动性提供者（LP）将被赋予在任意价格区间集中流动性的能力。这将提高池子的资金利用率，并允许LP估算他们认可的价格曲线，同时又与池子里剩余资金一起提供高效聚合的流动性。我们将分别在第2节和第6节描述该特性及其实现。

• 灵活的手续费：交易手续费将不再限定在0.30%。相反，手续费等级在每个池子初始化时设置，每一个交易对包含多个等级（池子）。默认支持手续费等级为0.05%，0.30%和1%。可以通过UNI治理增加新的手续费等级。

  注：UNI第9号提案申请引入新的手续费等级：0.01%，该提案已生效。0.01%的手续费适用于稳定币交易场景，使交易的滑点更小，这让Uniswap可以在稳定币交易领域直面Curve等市场龙头的竞争。

• 协议手续费治理：UNI治理可以灵活设置协议手续费对交易手续费的分成占比（参考6.2.2节）。

• 改进的价格预言机：Uniswap v3为用户提供了一种方式查询近期累计价格，从而避免了在计算TWAP（时间加权平均价格）的时间段开头和结尾手动记录累计价格。

• 流动性预言机：合约提供了一种时间加权平均流动性的预言机（参考5.3节）。

Uniswap v2 core合约被设计成不可升级的，因此Uniswap v3是在一组全新合约上实现。Uniswap v3合约同样是不可升级的，但允许一些参数被治理修改，我们将在第4节讨论。

2 Concentrated Liquidity 集中流动性

Uniswap v3的设计思想是集中流动性：流动性限制在某个价格区间。

在之前的版本中，流动性被均匀分布在以下曲线：

$$ x \cdot y = k \quad \text{(2.1)} $$

其中， $x$ 和 $y$ 是两种代币 $X$ 和 $Y$ 的余额， $k$ 是一个常数。换句话说，之前版本被设计为给整个价格区间 $(0, \infty)$ 提供流动性。这种方式容易实现，允许流动性被有效聚合，但也意味着池子中很多资产（流动性）永远不会被使用。

注：比如稳定币交易对，大部分时候价格波动极小，如果像Uniswap v2一样将流动性分散到所有价格区间 $(0, \infty)$，将导致资金利用率较低，因为大部分价流动性的价格区间永远不会被使用。

考虑到这个问题，允许LP将他们的流动性集中到更小的价格区间（而非 $(0, \infty)$）是合理的。我们将集中到一个有限区间的流动性称为“头寸”。一个头寸只需要维持足够的代币余额以支持该区间的交易即可，因此它与一个拥有更大代币余额（我们称为虚拟余额）的常值函数池子（在该价格区间）的运作方式很像。

注：可以将一个v3池子的区间想象成一个v2池子的一部分。

特别地，一个头寸只需要持有足够的代币 $X$ 以支持价格移动到其上限，因为当价格向上方移动时需要消耗 $X$ 代币。同样，只需要持有足够的代币 $Y$ 以支持价格移动到下限。图1描述了在价格区间 $\left[p_a, p_b\right]$ 的头寸与当前价格 $p_c \in \left[ p_a, pb \right]$ 的关系。 $x{real}$ 与 $y_{real}$ 代表头寸的真实代币余额。

当价格离开头寸区间时，该头寸的流动性将不再活跃，同时无法获得手续费。在该价格点上，流动性将完全只由一种代币组成，因为另一种代币都被耗尽。如果价格重新进入区间，流动性将再次变得活跃。

注：从图1可知，Uniswap常值函数池子的价格移动是以池子中两种代币余额的此消彼长来实现的，当价格（过高或过低）离开头寸区间，意味着其中一种代币被完全替换为另一种代币，因此此时区间中仅剩余一种代币。

流动性数量可以用 $L$ 衡量，其等价于 $\sqrt{k}$。头寸的真实代币余额可以用以下曲线表示：

$$ (x + \frac{L}{\sqrt(p_b)})(y + L \sqrt{p_a}) = L^2 \quad \text{(2.2)} $$

该曲线是公式2.1的变形，头寸只在自己的区间具有偿付能力（图2）。

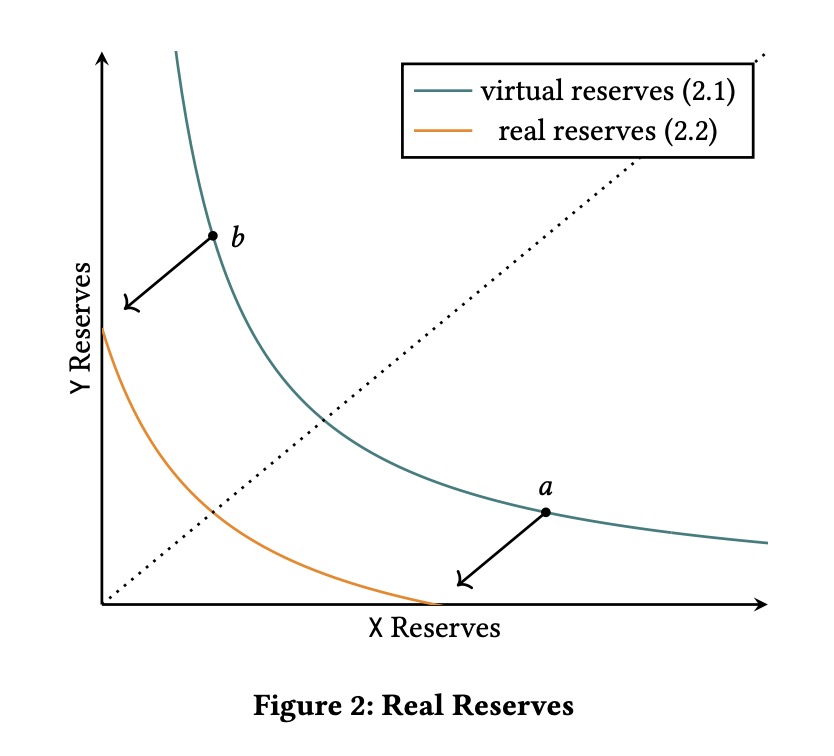
注：下面我们来推导公式2.2：

由图2可知，v3区间流动性曲线（图中real reserves曲线）实际上是将v2流动性曲线（图中virtual reserves曲线）通过坐标平移而来。假设在 $a$ ， $b$ 点的代币余额（reserves）（即坐标）分别为 $(x_a, y_a)$， $(x_b, y_b)$，则需要将v2曲线沿横坐标平移： $-x_b$ ，沿纵坐标平移： $-y_a$。

已知v2的曲线为：

$$x \cdot y = k$$

则平移后的v3曲线为：

$$(x + x_b) \cdot (y + y_a) = k \quad \text{(2.2.0)}$$

$a$, $b$点的价格分别为：

$$p_a = \frac{y_a}{x_a} \quad \text{(2.2.1)}$$

$$p_b = \frac{y_b}{x_b} \quad \text{(2.2.2)}$$

又因为：

$$x_a \cdot y_a = k \quad \text{(2.2.3)}$$

$$x_b \cdot y_b = k \quad \text{(2.2.4)}$$

因此，根据公式2.2.1和2.2.3可得：

$$y^2_a = k \cdot p_a$$

$$y_a = \sqrt{k} \cdot \sqrt{p_a} = L \sqrt{p_a}$$

根据公式2.2.2和2.2.4可得：

$$x^2_b = \frac{k}{p_b}$$

$$x_b = \frac{\sqrt{k}}{\sqrt{p_b}} = \frac{L}{\sqrt{p_b}}$$

由于：

$L = \sqrt{k}$，因此： $k = L^2$

将 $x_b$, $y_a$ 代入公式2.2.0，可得：

$$ (x + \frac{L}{\sqrt{p_b}})(y + L\sqrt{p_a}) = k = L^2 $$

只要流动性提供者觉得合适，他们可以自由地创建任意数量的头寸，每个头寸拥有自己的价格区间。通过这种方式，LP可以模拟价格空间中任意有分布需求的流动性（图3列举了部分例子）。此外，这种方式可以让市场决定流动性应该分配在什么地方。理智的LP们可以通过在当前价格附近的狭窄区间集中流动性来减少资金成本，并且通过添加或移除代币来移动价格，以使他们的流动性始终保持活跃。

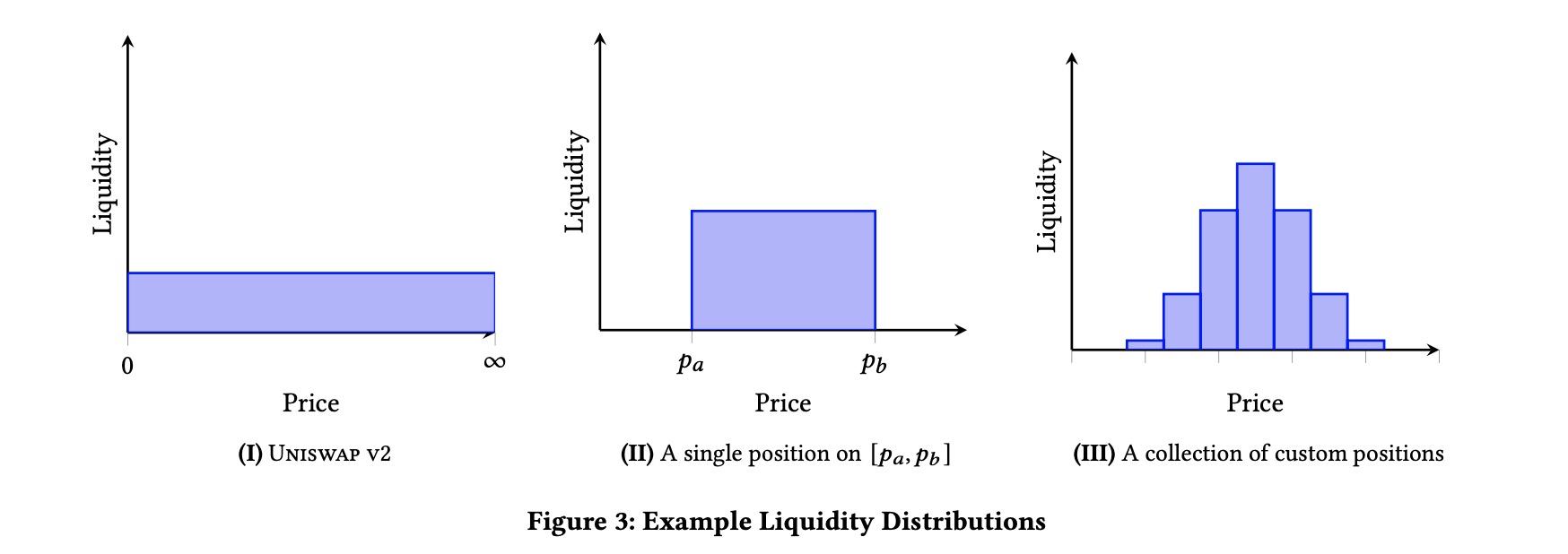
2.1 Range Orders 区间订单

在极小区间的头寸看起来非常像限价单，如果价格穿越区间，头寸将由完全为一种资产变成另一种资产（以及累计手续费）。区间订单与传统限价单有两点不同：

• 一个头寸的最小区间是有限制的。当价格正好位于头寸之内时，该限价单可能只有部分成交。

• 当头寸被穿越后，需要手动取回。否则，当价格再次回到区间时，头寸将自动反向交易。

注：如果价格反复穿越一个区间订单，头寸中的资产持仓将自动变化，从一种资产完全变成另一种资产，再反向变化，循环反复。而CEX的限价单在完全成交后，即使后期价格恢复，已成交的订单也不会回滚。

因此，如果需要实现像传统交易所一样的限价单效果，当价格穿越限价区间后，流动性提供者需要手动执行取回操作，才能完全获得另一种代币。或者可以使用第三方应用提供的自动取回功能，比如Gelato可以支持使用Uniswap v3的区间订单实现传统限价单的效果。

3 Architectural Changes 架构变动

Uniswap v3实现了许多架构改动，其中一部分改动是为了实现集中流动性而必须引入的，而另一部分则是独立的功能改进。

3.1 Multiple Pools Per Pair 多池交易对

在Uniswap v1和v2，每个交易对对应一个独立的流动性池子，并针对所有交易统一收取0.30%的手续费。虽然历史数据表明默认的手续费等级对于大部分代币都是合理的，但对于部分池子可能太高了（比如稳定币池子），而对于另一部分池子又太低了（比如高波动性或者冷门代币）。

Uniswap v3为每个交易对引入了多个池子，允许分别设置不同的交易手续费。所有池子都使用相同的工厂合约创建。默认允许创建三个手续费等级：0.05%，0.30%和1%。可以通过UNI治理添加更多手续费等级。

注：目前已经通过投票新增了一个0.01%的手续费等级。

3.2 Non-Fungible Liquidity 不可互换的流动性

3.2.1 非复利的手续费。之前版本的手续费收入会被作为流动性持续存入池子。这意味着即使没有主动存入，池子流动性也会随着时间而增长，并且可以复利地获取手续费收入。

在Uniswap v3，由于头寸的不可互换性，复利将变得不再可能。相反，手续费被独立保存，并且以支付手续费的代币形式持有（参考6.2.2）。

注：由于每个头寸的价格区间都不一样，因此v3的流动性不再像v2一样分布在所有价格区间，也就是说，v2流动性是可互换的，因此可以使用ERC-20代币表示。而v3流动性实际上是一个NFT（不可互换代币），使用ERC-721表示。

3.2.2 移除原生流动性代币。在Uniswap v1和v2，交易对池子合约本身是一个ERC-20合约，它的代币表示池子持有的流动性。虽然这种表示方式很方便，但它仍然与Uniswap v2的所倡导的理念有点不一致，即：任何不需要放在core合约的东西，都应该放到periphery合约，使用一个“标准”ERC-20的实现，阻止了后续创建ERC-20代币的优化版本。按理说，ERC-20代币实现应该放到periphery合约，再作为一个流动性头寸的封装放到core合约。

注：由于交易对合约的ERC-20实现在core合约中，并且是不可升级的，因此如果ERC-20的实现出现了bug，实际上会导致整个v2流动性受到影响。因此更好的方式是将ERC-20实现放到periphery合约中，而在core合约中仅存放一个wrapper引用，以便后续升级为新版本的ERC-20实现。

Uniswap v3引入的改动让可互换的流动性代币变成不可能。由于自定义流动性的特性，现在手续费以独立的代币被池子收集并持有，而不是自动复投为池子的流动性。

因此，v3的池子合约没有实现ERC-20标准。任何人都可以在periphery创建一种ERC-20代币合约，以便让流动性头寸变得更可互换，但这需要额外的逻辑来处理手续费收入的分发或再投资。或者，任何人都可以创建一个periphery合约，使用一种ERC-721 NFT代币表示个人流动性头寸（包括累计手续费）。

4 Governance 治理

工厂合约拥有一个owner（所有者），该地址初始时被UNI代币持有者控制。owner没有权限暂停core合约的任何操作。

注：在ETH主网，factory合约地址为0x1F98431c8aD98523631AE4a59f267346ea31F984，owner是一个TimeLock合约，地址为0x1a9C8182C09F50C8318d769245beA52c32BE35BC

与Uniswap v2相同，Uniswap v3也有可以被UNI治理打开的协议手续费。在Uniswap v3，UNI治理可以更灵活地设置协议获取的交易手续费比例，可以将协议手续费设置为 $\frac{1}{N}$的交易手续费或者0，其中， $4 \leq N \leq 10$。该参数可以基于每个池子设置。

注：Uniswap v2只能基于全局设置协议手续费，而Uniswap v3可以基于每个池子设置。

UNI治理可以添加额外的交易手续费等级。当添加一个手续费等级时，可以同时定义其对应的tickSpacing参数（参考6.1）。一旦手续费等级被添加进工厂合约，它就无法被移除（tickSpacing也无法被修改）。初始的手续费等级和tickSpacing分别为0.05%（tickSpacing为10，两个初始化tick之间约为0.10%），0.30%（tickSpacing为60，两个初始化tick之间约为0.60%），1%（tickSpacing为200，两个初始化tick之间约为2.02%）。

注：关于tick和tick spacing的概念，可以参考6.1节。

简单而言，每个tick（点）对应一个价格，为了聚合不同头寸的流动性，价格空间被划分为一个个可被初始化的tick，只有能被tickSpacing整除的tick才允许初始化；在tick内的交易机制与v2一样，当该tick的流动性被消耗以后，价格将进入下一个tick，并重复上述交易过程。因此tickSpacing越小意味着流动性越连续，交易滑点越小，但同时也带来了更大的gas消耗。

因此，每个手续费等级的tickSpacing是一个权衡值，但总体而言，越高的手续费等级，其tickSpacing越大。因为手续费越高，代表交易对的波动性越大，交易者能够承受的滑点也越大。

我们可以通过factory合约查看链上手续费配置：feeAmountTickSpacing，目前支持的feeAmount和tickSpacing分别为：{100: 1, 500: 10, 3000: 60, 10000: 200}。

我们在6.1节会提到，两个相邻tick的最小价格误差为0.01%。

最后，UNI治理有权利将owner转移给其他地址。

5 Oracle Upgrades 预言机升级

Uniswap v2引入了时间加权平均价格（TWAP）预言机功能，Uniswap v3的TWAP包括三个重要改动。

其中最重要的改动是Uniswap v3无需预言机用户在外部记录历史累计价格。Uniswap v2要求用户在需要计算TWAP的区间的开始和结束阶段分别记录累计价格。Uniswap v3将累计检查点放到core合约，允许外部合约直接计算最近一段时间的链上TWAP，无需额外保存累计价格。

另一个改动是Uniswap v3不再使用累计价格之和计算算术平均数TWAP，而是通过记录 $log$ 价格之和计算几何平均数TWAP。

注：我们在《深入理解Uniswap v2白皮书》中提到，几何平均数相比算术平均数，受极端值的影响更小，并且无需为每种代币记录单独的累计价格，因为一个代币的几何平均数价格是另一个的倒数。

最后，除了价格累计数外，Uniswap v3还增加了一个流动性累计数，每秒累计 $\frac{1}{L}$（即流动性倒数）。累计流动性对于那些基于Uniswap v3实现流动性挖矿的外部合约很有用。它也可以被其他合约用于判断一个交易对的哪个池子具有最可信的TWAP。

5.1 Oracle Observations 预言机观测

与Uniswap v2类似，Uniswap v3在每个区块开始记录累计价格，乘以自上一个区块到现在的时间（秒数）。

Uniswap v2的池子仅保存累计价格的最新值，该值由最近一个发生交易的区块更新。当在Uniswap v2计算平均价格时，需要由外部调用者负责提供提供累计价格的历史数据。如果有很多外部用户，每个用户都需要独立维护记录累计价格历史值的方法，或者使用一个共享方法减少成本。另外，无法保证每个有交互的区块都能影响累计价格。

在Uniswap v3，池子保存累计价格的一系列历史（如5.3节所述，也包括累计流动性）。在每个区块与池子第一次交互时，合约会自动记录累计价格，并且循环地使用新值覆盖数组中的最旧值，类似于一个环形缓冲区。虽然初始时数组仅分配一个检查点的空间，但是任何人都能够初始化额外的存储槽来扩展该数组，最多可达65,536个检查点。任何扩展该交易对检查点的人需要支付一次性的gas消耗来为数组初始化额外的存储槽。

注：扩展检查点空间的操作是一次性的，由发起操作的人支付。比如有人希望Uniswap v3的ETH-USDC交易对能够提供更多的历史价格检查点（检查点越多，意味着使用链上数据计算的预言机价格将越可信，因为攻击者要操纵这些价格所需的成本越高），以便通过链上可以获取预言机价格，他们就会调用ETH-USDC交易对的合约接口扩展检查点空间，并为此支付gas费用，因为该操作为交易对分配了额外的EVM存储槽空间。

交易对池子不仅向用户提供历史观测数据数组，还封装了一个便利函数用于在观测点周期内寻找任意时间点的累计价格。

5.2 Geometric Mean Price Oracle 几何平均数价格预言机

Uniswap v2维护两个累计价格，一个是以token1表示的token0价格，另一个则是以token0表示的token1价格。用户可以计算任意时间段的时间加权算术平均数价格，通过将区间结尾的累计价格减去开始的累计价格，并除以区间的时间（秒数）得出。注意token0和token1的累计价格是分别跟踪的，因为两个算术平均数价格不是互为倒数关系。

Uniswap v3使用时间加权的几何平均数价格，避免了为两个代币分别维护累计价格。一组比例数的几何平均数是该比例倒数的几何平均数的倒数。

注：假设池子里以token1表示的token0价格为 $x$ ，则以token0表示的token1价格为 $\frac{1}{x}$ ； $x_t$ 表示 $t$ 时刻的价格。

token0的几何平均数价格为： $$P_0 = \sqrt[n]{x_1 \cdot x_2 \cdot ... \cdot x_n}$$

token1的几何平均数价格为： $$P_1 = \sqrt[n]{\frac{1}{x_1} \cdot \frac{1}{x_2} \cdot ... \cdot \frac{1}{x_n}} = \frac{1}{\sqrt[n]{x_1 \cdot x_2 \cdot ... \cdot x_n}} = \frac{1}{P_0}$$

因此，两种代币的几何平均数价格互为倒数，Uniswap v3合约中只需要保存一种代币的累计价格即可。

由于自定义流动性供应的实现机制（参考第6节），在Uniswap v3实现几何平均数比较简单。此外，累计数能够用更少的比特位表示，因为它只记录 $\log{P}$而不是 $P$ ， $\log{P}$ 可以用相同精度表示更大范围的价格。最后，理论证明时间加权的几何平均数价格更能反映真实的平均价格。

注：为了以可接受的精度表示所有可能的价格，Uniswap v2使用224位比特的定点数表示价格。Uniswap v3仅需使用24位比特的有符号整数表示 $log_{1.0001}{P}$，同时可以识别一个基点即0.01%的价格变动。

如前文所述，市场价格本身是一种随机布朗运动，理论上使用几何平均数更能准确跟踪平均价格，因为算术平均数更容易受到极端值的影响而产生偏差。

Uniswap v3记录当前tick序号的累计和（ $\log{1.0001}{P}$ ，即以1.0001为底的价格 $P$ 对数，它可以识别1个基点即0.01%的价格变化），而不是记录累计价格 $P$ 。任意时间点的累计数等价于该合约截止当前时间每秒对数价格（ $\log{1.0001}(P)$ ）之和：

$$ at = \sum{i=1}^{t} \log_{1.0001}(P_i) \quad \text{(5.1)} $$

注：为什么 $log_{1.0001}P$ 能够识别的价格变化精度为0.01%（即1个基点）呢？

因为Uniswap v3使用int24（24位有符号整数）表示tick，假设当前tick为 $i$ ，对应的价格为 $P_1$ ；下一个最近的tick为 $i + 1$ ，对应的价格 $P_2 = P_1 \cdot 1.0001$ ，其相对 $P_1$ 的价格变化精度为：

$$ \frac{P_2 - P_1}{P_1} = \frac{P_1 \cdot 1.0001 - P_1}{P_1} = 1.0001 - 1 = 0.0001 = 0.01\% $$

任意时间段 $t_1$ 到 $t2$ 的几何平均价格（时间加权平均价格） $(p{t_1,t_2})$ 为：

$$ P_{t_1,t_2} = \left(\prod^{t2}{i=t_1} P_i \right)^{\frac{1}{t_2 - t_1}} \quad \text{(5.2)} $$

注：这里我们回顾一下几何平均数的定义：

几何平均数 Geometric Mean：

$$ G(x_1,...,x_n) = \sqrt[n]{x_1 ... x_n} $$

可以看出 $P_{t_1,t_2}$ 即为 $t_1$ 至 $t_2$ 时间段的几何平均价格。

为了计算这个值，你可以分别查看 $t_1$ 和 $t_2$ 时刻的累计价格，将后者减去前者，并除以时间差（秒数），最后计算 $1.0001^x$ 得出时间加权几何平均价格：

$$ \log{1.0001}(P{t_1,t2}) = \frac{\sum{i=t_1}^{t2} \log{1.0001}(P_i)}{t_2 - t_1} \quad \text{(5.3)} $$

$$ \log{1.0001}(P{t_1,t2}) = \frac{a{t2} - a{t_1}}{t_2 - t_1} \quad \text{(5.4)} $$

$$ P_{t_1,t2} = 1.0001^{\frac{a{t2} - a{t_1}}{t_2 - t_1}} \quad \text{(5.5)} $$

5.3 Liquidity Oracle 流动性预言机

除了每秒加权的累计数 $\log{1.0001}price$ ，Uniswap v3在每个区块的开头还记录了一个每秒加权的流动性倒数 $\frac{1}{L}$ （当前区间的虚拟流动性倒数）累计数：secondsPerLiquidityCumulative( $s{pl}$ )。

这个计数可以被外部流动性挖矿合约使用，以便公平地分配奖励。如果一个外部合约希望以每秒 $R$ 个代币的平均速率分配给合约中所有活跃的流动性，假设一个头寸从 $t_0$ 到 $t1$ 的活跃流动性为 $L$ ，则其在该时间段应该获得的奖励为： $R \cdot L \cdot (s{pl}(t1) - s{pl}(t_0))$。

注： $s_{pl}(t)$ 表示：截止到 $t$ 时刻，（池子）平均每份流动性持续的总时长（秒数）。

$(s_{pl}(t1) - s{pl}(t_0))$ 表示： $t_0$ 至 $t_1$ 这个时间段，（池子）平均每份流动性持续的总时长（秒数）。

$R \cdot (s_{pl}(t1) - s{pl}(t_0))$表示：在 $t_0$ 至 $t_1$ 时间段，平均每份流动性获得的奖励。

由于该头寸的活跃流动性为 $L$ ，因此，其在 $t_0$ 至 $t_1$ 时间段获得的奖励为：

$$R \cdot L \cdot (s_{pl}(t1) - s{pl}(t_0)) $$

为了扩展这个公式，实现仅当流动性在头寸区间时才能获得奖励，Uniswap v3在每次tick被穿越时会保存一个基于该值计算后的检查点，我们将在第6.3节介绍。

链上合约可以使用该累计数，以使他们的预言机更健壮（比如用于评估哪个手续费等级的池子更适合被作为预言机数据源）。

6 Implementing Concentrated Liquidity 实现集中流动性

本文剩余部分将介绍集中流动性供应的实现机制，同时简要介绍其在合约是如何实现的。

6.1 Ticks and Ranges 点和区间

为了实现自定义流动性供应，可能的价格空间被离散的点（tick）划分。流动性提供者可以在任意两个（无需是临近的）tick定义的区间提供流动性。

注：在交易系统中，tick size 表示价格变动的最小单位。如果某股票的最小价格变动单位是 \$0.01，那么其价格只能从 \$100.00 到 \$100.01 。在 Uniswap V3 中，这里价格 \$100.00 和 \$100.01 对应两个 tick，而价格最小变动单位 \$0.01 则相当于 tick space。

每个区间可以被一对（有符号整数）tick序号（tick indices）定义：一个低点（ $i_l$ ）和一个高点（ $i_u$ ）。tick表示能够被合约虚拟流动性修改的价格。我们将假设价格总是以token1表示的token0的形式。token0和token1的赋值是任意的，不影响合约的逻辑（除了可能的舍入误差）。

从概念上，每当价格 $p$ 等于1.0001的整数次方时就存在1个tick（点）。我们使用整数 $i$ 表示tick（点），使得该点的价格可以表示为：

$$ p(i) = 1.0001^i \quad \text{(6.1)} $$

根据定义，两个相邻的tick之间的价格移动精度为0.01%（1个基点）。

注：见5.2节的公式推导。

由于6.2.1节中描述的技术原因，交易对池子实际上使用开根号价格 $\sqrt{price}$ 来跟踪tick（点），该值等于 $\sqrt{1.0001}$ 的整数次方。可将上述等式转换为等价的开根号价格形式：

$$ \sqrt{p}(i) = \sqrt{1.0001}^i = 1.0001^{\frac{i}{2}} \quad \text{(6.2)} $$

举个例子， $\sqrt{p}(0)$ （tick 0的开根号价格）等于1， $\sqrt{p}(0)$ 等于 $\sqrt{1.0001} \approx 1.00005$ ， $\sqrt{p}(-1)$ 等于 $\frac{1}{\sqrt{1.0001}} \approx 0.99995$ 。

当流动性加入一个区间，如果其中一个或全部tick都没有被已存在的头寸用作边界点，该tick将被初始化。

不是每个tick都能被初始化。交易对池子在初始化时有一个参数tickSpacing( $t_s$ )；只有那些序号能够被tickSpacing整除的tick才能被初始化。比如，如果tickSpacing是2，则只有偶数tick (...-4, -2, 0, 2, 4...)能被初始化。小的tickSpacing允许更严格和更精确的区间，但可能导致每次交易消耗更多gas（因为每次交易穿越一个初始化的tick时，都需要给操作方带来gas消耗）。

注：可以把 tick spacing 理解为交易系统中的 tick size，即价格变动的最小单位。tick spacing 越小，意味着价格变动的最小单位越小，交易滑点也越小，但同时也带来了更大的gas消耗。

任何时候价格穿越一个初始化的tick时，虚拟流动性将被加入或者移除。穿越一个初始化的tick所带来的gas消耗是固定的，与在该tick添加或移除虚拟流动性的头寸数量无关。

为了确保当价格穿越tick时，能够添加和移除正确数量的流动性；同时也为了确保当头寸在价格区间内时，能够正确获取对应比例的手续费收入，交易对池子需要一些记账工作。交易对合约使用存储变量来分别记录全局（每个池子）级别、每个tick级别和每个头寸级别的状态。

6.2 Global State 全局状态

合约的全局状态包括7个与交换和流动性供应相关的存储变量。（它也有其他一些存储变量用于预言机，如第5节描述。）

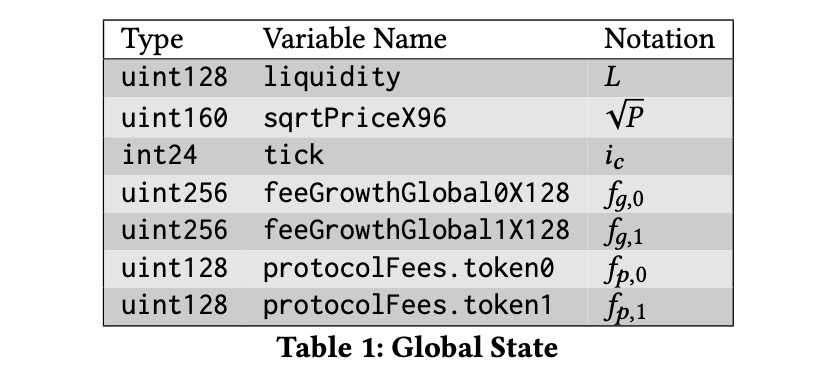
6.2.1 Price and Liquidity 价格和流动性

在Uniswap v2，每个池子合约记录池子当前的代币余额： $x$ 和 $y$ 。而在Uniswap v3，合约可以被当作拥有虚拟余额， $x$ 和 $y$ 值用于描述合约行为（在两个相邻的tick之间），就好像它仍遵循常值函数。

注：Uniswap v3实际上只在一段价格区间内遵循常值函数。

交易对合约记录两个不同值：流动性liquidity（ $L$ ）和开根号价格sqrtPrice（ $\sqrt{P}$ ），而不是虚拟余额。这两个值可根据虚拟余额计算如下：

$$ L = \sqrt{xy} \quad \text{(6.3)} $$

$$ \sqrt{P} = \sqrt{\frac{y}{x}} \quad \text{(6.4)} $$

反过来，两种代币的虚拟余额也可以使用这两个值计算得出：

$$ x = \frac{L}{\sqrt{P}} \quad \text{(6.5)} $$

$$ y = L \cdot \sqrt{P} \quad \text{(6.6)} $$

使用 $L$ 和 $\sqrt{P}$ （而不是 $x$ 和 $y$ ）计算比较方便，因为一个时刻只有其中一个值会变化。当在一个tick内交易时，只有价格（即 $\sqrt{P}$ ）发生变化；当穿越一个tick或者铸造/销毁流动性时，只有流动性（即 $L$ ）发生变化。这避免了在记录虚拟余额时可能遇到的舍入误差问题。

注：请一定理解这句话，这是 Uniswap v3 的核心： 任意时刻， $L$ 和 $\sqrt{P}$ 只有其中一个值会变化。 在 swap 时，所有处于当前价格区间的流动性构成总流动性；每个 swap 将拆成多个 step，每个 step 只在一个 tick 区间内执行 swap 操作，因此在 swap 时， $L$ 不变， $\sqrt{P}$ 变化；当价格穿越 cross tick 时，修改总流动性 $L$ ，保持 $\sqrt{P}$ 不变，再继续进行下一个 swap step；同时在 add/burn liquidity 时， $L$ 变化， $\sqrt{P}$ 不变。

你可能注意到（基于代币虚拟余额的）流动性公式（即公式6.3）与Uniswap v2用于初始化流动性代币数量的公式类似（当还没有任何手续费收入时）。流动性可以被看作虚拟流动性代币。

同样，流动性也可以被看作token1的（无论是真实还是虚拟的）数量变化与价格 $\sqrt{P}$ 变化的比例：

$$ L = \frac{\Delta{Y}}{\Delta{\sqrt{P}}} \quad \text{(6.7)} $$

注：根据公式6.6，假设 $t_0$ 和 $t_1$ 时刻，对应的 $y_0$ 和 $y_1$ 分别为：

$y_0 = L \cdot \sqrt{P_0}$

$y_1 = L \cdot \sqrt{P_1}$

因此：

$y_1 - y_0 = L \cdot (\sqrt{P_1} - \sqrt{P_0})$

转换后即可得出公式6.7：

$$ L = \frac{y_1 - y_0}{\sqrt{P_1} - \sqrt{P_0}} = \frac{\Delta{Y}}{\Delta{\sqrt{P}}} $$

我们记录 $\sqrt{P}$ 而不是 $P$ 正式为了利用上述公式，如6.2.3节描述，这样也可以避免当计算交易时进行任何开根号运算。

全局状态记录当前tick序号为 $tick(i_c)$ ，一个表示当前tick的有符号整数（更准确地说，是低于当前价格的最接近的tick）。这是一种优化策略（也是一种避免对数精度问题的方法），因为在任意时刻，你需要能够基于当前的开根号价格 $sqrtPrice$ 计算出对应的tick。在任意时间点，以下等式总是成立：

$$ ic = \lfloor \log{\sqrt{1.0001}} \sqrt{P} \rfloor \quad \text{(6.8)} $$

注：根据公式6.2:

$\sqrt{p}(i) = \sqrt{1.0001}^i$，

因此：

$i = \log_{\sqrt{1.0001}} \sqrt{P}$

而i是整数，所以还需要（向下）取整。

6.2.2 Fees 手续费

每个交易对池子初始化时会设置一个不可修改的手续费（ $\gamma$ ），表示交易者需要支付的手续费，以百分之一基点为一个单位（0.0001%）。

注：默认的手续费值为500，3000，10000，分别表示的手续费为：500 x 0.0001\% = 0.05\%, 3000 x 0.0001\% = 0.30\%, 1000 x 0.0001\% = 1\%。

另一个变量为协议手续费 $\phi$ ，初始时设置为0，但是可以通过 UNI 治理修改。该数字表示交易者支付手续费的部分比例将分给协议，而不是流动性提供者。 $\phi$ 只允许被设置为以下几个合法值：0, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9 或者 1/10。

注：协议手续费开关无法在创建交易对的时候自动打开，只能由UNI治理针对具体池子单独执行手续费设置，并且可以针对不同池子分别设置协议手续费。

全局状态还记录两个值：feeGrowthGlobal0 ( $f{g,0}$ )和feeGrowthGlobal1 ( $f{g,1}$ )。他们表示该合约到现在为止，每一份虚拟流动性（ $L$ ）获取的手续费。你可以把他们理解为当合约第一次初始化时，每一份添加的非边界的流动性所获取的所有手续费。使用无符号定点数（128x128格式）表示。注意，在Uniswap v3，手续费是以原生代币形式收集，而不是流动性代币的形式（请参考3.2.1节）。

最后，全局状态记录以每种代币表示的累计未被领取的协议手续费：protocolFees0 ( $f{p,0}$ )和protocolFees1 ( $f{p,1}$ )。该变量以无符号uint128类型表示。累计协议手续费可以通过UNI治理领取，通过调用collectProtocol方法。

6.2.3 Swapping Within a Single Tick 在一个Tick内交易

对于那些无法使价格变化超过一个tick（点）的小额交易，该合约像一个 $x \cdot y = k$ 池子一样工作。

假设 $\gamma$ 是交易手续费，比如0.003， $y_{in}$ 是传入的token1代币数量。

首先，feeGrowthGlobal1和protocolFees1将增加：

$$ \Delta{f{g,1}} = y{in} \cdot \gamma \cdot (1 - \phi) \quad \text{(6.9)} $$

$$ \Delta{f{p,1}} = y{in} \cdot \gamma \cdot \phi \quad \text{(6.10)} $$

注： $\phi$ 是协议手续费占手续费的比例，因此协议手续费比例为： $\gamma \cdot \phi$ ，协议手续费收入为公式6.10。

剩余的手续费分给流动性提供者，即扣除协议手续费后的交易手续费，其比例为： $\gamma \cdot (1 - \phi)$，交易手续费收入为公式6.9。

$\Delta y$ 是 $y$ 的增加量（当手续费扣除后）。

$$ \Delta{y} = y_{in} \cdot (1 - \gamma) \quad \text{(6.11)} $$

如果你用经过计算的虚拟余额（ $x$ 和 $y$ ）为token0和token1的数量，以下公式可以计算出交易后的token0的代币数量：

$$ x_{end} = \frac{x \cdot y}{y + \Delta{y}} \quad \text{(6.12)} $$

注：因为在1个tick内，交易符合k常值函数，即：

$$x{end} \cdot y{end} = x \cdot y$$

因此可推出：

$$x{end} = \frac{x \cdot y}{y{end}} = \frac{x \cdot y}{y + \Delta{y}}$$

但是请注意，在v3，合约使用流动性（ $L$ ）和开根号价格（ $\sqrt{P}$ ）代替 $x$ 和 $y$ 。我们可以使用这两个值计算 $x$ 和 $y$ ，然后计算交易的成交价格。但是，对于给定的 $L$ ，我们可以推导出简洁的等式描述 $\Delta{\sqrt{P}}$ 和 $\Delta{y}$ 的关系（可根据公式6.7推出）：

$$ \Delta{\sqrt{P}} = \frac{\Delta{y}}{L} \quad \text{(6.13)} $$

$$ \Delta{y} = \Delta{\sqrt{P}} \cdot L \quad \text{(6.14)} $$

同时可以推导出 $\Delta{\frac{1}{\sqrt{P}}}$ 和 $\Delta{x}$ 的关系：

$$ \Delta{\frac{1}{\sqrt{P}}} = \frac{\Delta{x}}{L} \quad \text{(6.15)} $$

$$ \Delta{x} = \Delta{\frac{1}{\sqrt{P}}} \cdot L \quad \text{(6.16)} $$

注：根据公式6.5，假设 $t_0$ 和 $t_1$ 时刻，对应的 $x_0$ 和 $x_1$ 分别为：

$x_0 = \frac{L}{\sqrt{P_0}}$

$x_1 = \frac{L}{\sqrt{P_1}}$

因此：

$x_1 - x_0 = L \cdot (\frac{1}{\sqrt{P_1}} - \frac{1}{\sqrt{P_0}})$

转换后即可得公式6.16：

$$ \Delta{x} = L \cdot \Delta{\frac{1}{\sqrt{P}}} $$

当使用一种代币交换另一种时，交易对合约可以先根据公式6.13或6.15计算新的开根号价格 $\sqrt{P}$ ，接着根据公式6.14或6.16计算需要转出的token0和token1代币数量。

对于任意交易，只要交易后的开根号价格 $\sqrt{P}$ 没有进入下一个初始化的tick所在的价格，上述公式都可以正常工作。如果计算后的 $\Delta{\sqrt{P}}$ 将使得 $\sqrt{P}$ 进入下一个初始化的tick，合约将完成当前tick（仅占一部分交易），再继续进入下一个tick完成剩余的交易，参考6.3.1节。

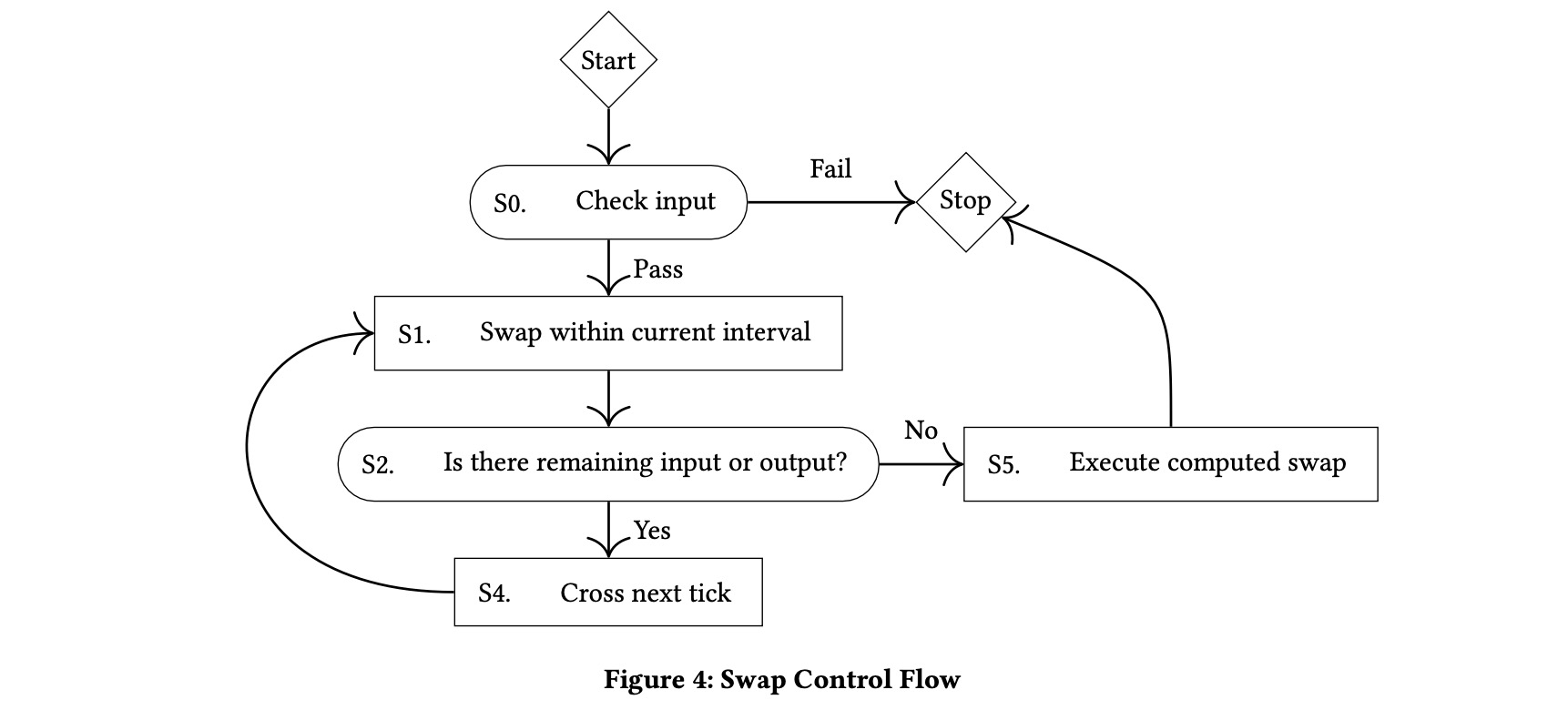
6.2.4 Initialized Tick Bitmap 初始化Tick的位图

如果一个tick没有被用作流动性区间的边界点（即如果该tick没有被初始化），那么在交易过程中可以跳过这个tick。

为了更高效寻找下一个已初始化的tick，合约使用一个位图tickBitmap记录已初始化的tick。如果tick已被初始化，位图中对应于该tick序号的位置设置为1，否则为0。

当tick被一个新头寸用作边界点，并且该tick没有被任何其他流动性使用，那么它将被初始化，位图中对应的比特位置为1。当该点关联的流动性都被移除时，已初始化的tick将重新变成未初始化，位图中对应的比特位置为0。

6.3 Tick-Indexed State Tick索引状态

为了记录每个tick被穿越时需要添加和移除的净流动性，以及在大于和小于该tick时所挣取的手续费，合约需要额外保存每个tick相关的信息。

合约保存一个映射表，每个tick序号对应以下7个变量：

每个tick记录 $\Delta{L}$ ，表示当该tick被完全穿越时需要加入和移除的总流动性数量。Tick只需要记录一个有符号整数：当交易促使tick值从左到右移动时，需要往该tick注入的流动性（反之，当tick值从右到左移动时，该值为负，表示移除流动性）。该值无需在每次价格穿越tick时更新（只需在使用该tick作为边界点的头寸更新时才更新）。

当tick没有流动性关联时，我们希望对其取消初始化。因为 $\Delta{L}$ 是一个净值，还需要记录该tick关联的总流动性：liquidityGross。该值确保即使净流动性为0，我们仍能知道该tick是否被至少一个头寸关联，以此决定是否更新tick位图。

feeGrowthOutside{0, 1}用于记录一个给定区间总共累计多少手续费。因为token0和token1收集手续费的公式相同，我们在本节剩余的公式中将忽略（token0和token1）下标。

根据当前价格是否在区间内，你可以使用一个公式计算每份流动性在tick $i$ 之上（ $f_a$ ）和之下（ $f_b$ ）获取的手续费（根据当前tick序号 $i_c$ 是否大于等于 $i$ ）：

$$ f_a(i) = \begin{cases} f_g - f_o(i) & \text{$i_c \geq i$}\ f_o(i) & \text{$i_c < i$} \end{cases} \quad \text{(6.17)} $$

$$ f_b(i) = \begin{cases} f_o(i) & \text{$i_c \geq i$}\ f_g - f_o(i) & \text{$i_c < i$}\end{cases} \quad \text{(6.18)} $$

注： 首先回顾一下每个变量的含义， $f_g$ 是（每个流动性）全局累计手续费； $f_o(i)$ 是在指定tick $i$之外（每个流动性）累计的手续费，需特别注意，该值随着当前tick $i_c$变化后会改变表示的方向。

当 $i_c < i$ 时，

$$ \underbrace{\overbrace{i_c, ..., i - 1}^{f_b(i) = f_g - f_o(i)}, i, \overbrace{i + 1, ...}^{f_a(i)=fo(i)}}{f_g} $$

当 $i_c \geq i$ 时，

$$ \underbrace{\overbrace{..., i - 1}^{f_b(i) = f_o(i)}, i, \overbrace{i + 1, ..., i_c}^{f_a(i)=f_g - fo(i)}}{f_g} $$

我们可以使用上述函数计算任意两个tick（低点tick $i_l$和高点tick $i_u$）区间内，每个流动性累计的全部手续费 $f_r$：

$$ f_r = f_g - f_b(i_l) - f_a(i_u) \quad \text{(6.19)} $$

注：根据上述推论，我们可以画出几个手续费的逻辑关系如下：

$$ \underbrace{\overbrace{..., i_l - 1}^{f_b(i_l)}, \overbrace{i_l, i_l + 1, ..., i_u - 1, i_u}^{f_r}, \overbrace{i_u + 1, ...}^{f_a(iu)}}{f_g} $$

根据公式 (6.17) (6.18) (6.19) 以及 $i_c$ 和 $i_l$、$i_u$ 的关系，可以总结区间内的手续费计算方式如下： $$ f_r = \begin{cases} f_o(i_l) - f_o(i_u) & \text{$i_c < i_l < i_u$}\ f_g - f_o(i_l) - f_o(i_u) & \text{$i_l \leq i_c < i_u$}\ f_o(i_u) - f_o(i_l) & \text{$i_l < i_u \leq i_c$} \end{cases} $$

$f_o$ 需要在每次tick穿越时被更新。特别地，当tick被反方向穿越时，其对应的 $f_o$（token0和token1）需要按照如下方式更新：

$$ f_o(i) := f_g - f_o(i) \quad \text{(6.20)} $$

只有被至少一个头寸作为边界端点的tick才需要 $f_o$。因此，出于效率考虑， $f_o$ 不会被初始化（当tick被穿越时无需被更新），只有当使用该tick作为边界点创建头寸时才会初始化。当tick $i$的 $f_o$ 初始化时，它的初始值被设置成当前所有的手续费都由小于该tick时收取：

$$ f_o := \begin{cases} f_g & \text{$i_c \geq i$}\ 0 & \text{$i_c < i$} \end{cases} \quad \text{(6.21)} $$

注意，因为不同tick的 $f_0$ 值可以在不同时刻初始化，因此比较他们的 $f_0$ 是无意义的，实际上无法保证 $f_0$ 值不变。但这不会导致每个头寸的统计问题，如下文描述，所有的头寸只需要知道从上一次交互后，区间内的 $g$ 值增长即可。

最后，合约同时为每个tick保存secondsOutside ( $s_o$ )，secondsPerLiquidityOutside和tickCumulativeOutside。这些变量不会被合约内部使用，而是帮助外部合约（如基于v3的流动性挖矿合约）更方便地获取合约信息。

这三个变量于上文提到的手续费增长变量类似。但是不同于feeGrowthOutside{0, 1}跟踪feeGrowthGlobal{0, 1}，secondsOutside跟踪seconds（也就是当前时间戳），secondsPerLiquidityOutside跟踪5.3节中描述的 ${1}/{L}$ 累计数（secondsPerLiquidityCumulative）；tickCumulativeOutside跟踪第5.2节中描述的 $\log_{1.0001}P$ 累计数。

比如，对于一个给定的tick，根据当前价格是否在区间内， $s_a$ 与 $s_b$ 分别为大于与小于tick $i$时持续的时长（秒数）， $s_r$ 为区间内持续的秒数，其计算方式分别为：

$$ t_a(i) = \begin{cases} t - t_o(i) & \text{$i_c \geq i$}\ t_o(i) & \text{$i_c < i$} \end{cases} \quad \text{(6.22)} $$

$$ t_b(i) = \begin{cases} t_o(i) & \text{$i_c \geq i$}\ t - t_o(i) & \text{$i_c < i$}\end{cases} \quad \text{(6.23)} $$

$$ t_r(i_l, i_u) = t - t_b(i_l) - t_a(i_u) \quad \text{(6.24)} $$

在 $t_1$ 到 $t_2$ 时间段内，头寸在价格区间内的持续时间可以通过记录 $t_1$ 和 $t_2$ 时间点的 $s_r(i_l, i_u)$ 值，并将后者减去前者得到。

和 $f_o$ 类似，对于不是头寸边界点的tick无需记录 $s_o$。因此，只有使用该tick作为边界点的头寸创建时，才需要初始化 $s_o$。为了方便，初始的默认值为截止到当前时间的秒数，并都发生在小于该tick的时候：

$$ t_o(i) := \begin{cases} t & \text{$i_c \geq i$}\ 0 & \text{$i_c < i$} \end{cases} \quad \text{(6.25)} $$

与 $f_o$ 值类似，比较不同tick的 $t_o$ 值也是无意义的。仅当计算一个时间段（起始时间需在两个tick的 $t_0$ 初始化之后）的指定价格区间的流动性持续时间时， $t_0$ 才是有意义的。

6.3.1 Crossing a Tick 穿越一个Tick

如6.2.3节描述，当在初始化的tick之间交易时，Uniswap v3可以像 $k$ 常值函数一样工作。但是，当交易穿越一个已初始化的tick时，合约需要添加或移除流动性，以确保没有流动性提供者会破产。这意味着 $\Delta{L}$ 是从tick中提取，并应用到全局 $L$ 中。

为了记录在价格区间内时，该tick作为边界点的手续费收入（和持续时间），合约需要更新tick的状态。feeGrowthOutside{0, 1}和secondsOutside被更新到反映当前值，当与该tick关联的交易方向改变时，按照下述公式更新：

$$ f_o := f_g - f_o \quad \text{(6.26)} $$

$$ t_o := t - t_o \quad \text{(6.27)} $$

当一个tick被穿越后，如6.2.3节描述，交易将继续直到碰到下一个已初始化的tick。

6.4 Position-Indexed State 头寸索引状态

合约记录一个映射表，从用户地址，头寸低点（左边界，一个tick序号，int24类型）和高点（右边界，一个tick序号，int24类型）到具体头寸信息的映射关系。每个头寸记录三个值：

liquidity（ $l$ ）表示上一次头寸更新时，该头寸所表示的虚拟流动性数量。特别地，liquidity可以被看作 $\sqrt{x \cdot y}$，其中 $x$ 和 $y$ 分别表示在任意时刻该头寸进入价格区间时，由对应的虚拟token0和token1数量表示的加入池子的流动性。与Uniswap v2不同（每个流动性份额随时间增长），v3的流动性份额并不改变，因为手续费是单独累计；它总是等价于 $\sqrt{x \cdot y}$，其中， $x$ 和 $y$ 分别表示token0和token1的数量。

liquidity（流动性）数量不代表从合约上次交互后的累计手续费，uncollected fees才用于表示未领取的手续费。为了计算未领取的手续费，需要在头寸保存额外信息，如feeGrowthInside0ast（ $f_{r,0}(to)$ ）和feeGrowthInside1Last( $f{r,1}(t_0)$ )，如下文所述。

6.4.1 setPosition 设置头寸

setPosition方法允许流动性提供者更新他们的头寸。

setPosition的两个参数：lowerTick和upperTick，与调用者msg.sender一起组成了头寸的信息。

该方法接受一个额外参数：liquidityDelta，用于指定用户希望添加或移除（负值）的虚拟流动性。

首先，该方法计算头寸的未领取手续费（ $f_u$ ）（分别以两种代币表示）。头寸所有者获取的手续费，将其减去用户添加或移除虚拟流动性，即为净收入。

为了计算一个代币的未领取手续费，你需要知道自从上一次领取手续费后，该头寸对应的区间获得多少手续费 $f_r$（如6.3描述，使用区间 $i_l$, $i_r$计算）。从 $t_0$ 到 $t_1$ 时间段，区间内每份流动性的的手续费增长为： $f_r(t_1) - f_r(t_0)$（其中， $f_r(t_0)$ 在头寸中以feeGrowthInside{0, 1}Last保存， $f_r(t_1)$ 能够从当前tick状态中计算）。将其乘以头寸的流动性，即为以token0表示的该头寸未领取的手续费：

$$ f_u = l \cdot (f_r(t_1) - f_r(t_0)) \quad \text{(6.28)} $$

接着，合约将liquidityDelta加到头寸的liquidity（流动性）。在tick区间低点，它同时将liquidityDelta加到liquidityNet（注：tick从左到右，表示加入流动性）；而在头寸的高点，则从liquidityNet减去liquidityDelta（注：tick从右到左，表示移除流动性）。如果池子当前价格在头寸区间内，合约也会将liquidity加到全局的globalLiquidity。

最后，根据销毁或铸造的流动性数量，池子将代币从用户转出（如果liquidityDelta是负值，则将代币转给用户）。

如果价格从当前价格（ $P$ ）移动到高点或低点，需要存入的token0（ $\Delta{X}$ ）和token1（ $\Delta{Y}$ ）代币的数量可以被看作从头寸中卖出对应数量的代币。根据价格是否低于区间、在区间内或者高于区间，可以从6.14节和6.16节公式推出以下公式：

$$ \Delta{Y} = \begin{cases} 0 & \text{$i_c < i_l$}\ \Delta{L} \cdot (\sqrt{P} - \sqrt{p(i_l)}) & \text{$i_l \leq i_c \leq i_u$}\ \Delta{L} \cdot (\sqrt{p(i_u)} - \sqrt{p(i_l)}) & \text{$i_c \geq i_u$} \end{cases} \quad \text{(6.29)} $$

$$ \Delta{X} = \begin{cases} \Delta{L} \cdot (\frac{1}{\sqrt{p(i_l)}} - \frac{1}{\sqrt{p(i_u)}}) & \text{$i_c < i_l$}\ \Delta{L} \cdot (\frac{1}{\sqrt{P}} - \frac{1}{\sqrt{p(i_u)}}) & \text{$i_l \leq i_c \leq i_u$}\ 0 & \text{$i_c \geq i_u$} \end{cases} \quad \text{(6.30)} $$

引用文献

• [1] Hayden Adams, Noah Zinsmeister, and Dan Robinson. 2020. Uniswap v2 Core. Retrieved Feb 24, 2021 from https://uniswap.org/whitepaper.pdf
• [2] Guillermo Angeris and Tarun Chitra. 2020. Improved Price Oracles: Constant Function Market Makers. In Proceedings of the 2nd ACM Conference on Advances in Financial Technologies (AFT ’20). Association for Computing Machinery, New York,NY,UnitedStates, 80–91. https://doi.org/10.1145/3419614.3423251
• [3] Michael Egorov. 2019. StableSwap - Efficient Mechanism for Stablecoin Liquidity. Retrieved Feb 24, 2021 from https://www.curve.fi/stableswap-paper.pdf
• [4] Allan Niemerg, Dan Robinson, and Lev Livnev. 2020. YieldSpace: An Automated Liquidity Provider for Fixed Yield Tokens. Retrieved Feb 24, 2021 from https://yield.is/YieldSpace.pdf
• [5] Abraham Othman. 2012. Automated Market Making: Theory and Practice. Ph.D. Dissertation. Carnegie Mellon University.

• 本文转载自： github.com/adshao/public...