Merkle树、Merkle证明和Merkle根的综合指南

Merkle 树、Merkle 证明和 Merkle 根是什么

深入探讨 Merkle 树的数据结构以及 Merkle 证明如何验证数据的存在。回答以下问题：什么是 Merkle 树、Merkle 证明和 Merkle 根？

什么是 Merkle 树、Merkle 证明和 Merkle 根？了解它们是什么、如何工作以及如何将它们应用于你的项目中。

通过这篇文章的学习，你将理解 Merkle 树、Merkle 证明和 Merkle 根是什么，为什么需要它们，如何使用它们，以及如何将它们构建到你的项目中！让我们开始吧！

在开始之前，请确保你对以下内容有扎实的理解：

• 哈希函数的知识
• 精通 Solidity 智能合约

‍

什么是 Merkle 树、Merkle 证明和 Merkle 根？

‍

我们为什么需要 Merkle 树？

问题：我如何验证某些任意数据是否在一组数据中？例如，假设我们有一个俱乐部 VIP 名单，我们如何确定特定的名字是否在名单上？

我们难道不能简单地遍历（或手动搜索）数据列表来检查我们正在寻找的特定数据是否存在？

这将是一个挑战，尤其是当名字列表非常庞大时（想想成千上万）。现在，想象一下这是一个智能合约中的字符串数组。遍历这个数组的成本会随着名字数组的增加而变得极其高昂。在某些情况下，可能会出现服务拒绝，导致无法检查某个名字，因为 gás 不够。相反，我们使用 Merkle 树！

‍

Merkle 树是什么？

Merkle 树是一种数据结构，而 Merkle 证明则用于证明某些数据在该 Merkle 树中。它们是在1979年由 Ralph Merkle 发明的，他是一位计算机科学家、数学家，也是公钥密码学的创造者之一。

那么，Merkle 树实际是什么呢？

想象一棵树……但是是倒过来的。

叶子位于底部，根位于顶部。我们树中的每个叶子都是一条数据，树的分支和根通过将这些数据进行 哈希 得到。这就是 Merkle 树。通过这篇文章，你将理解下面这个图示：

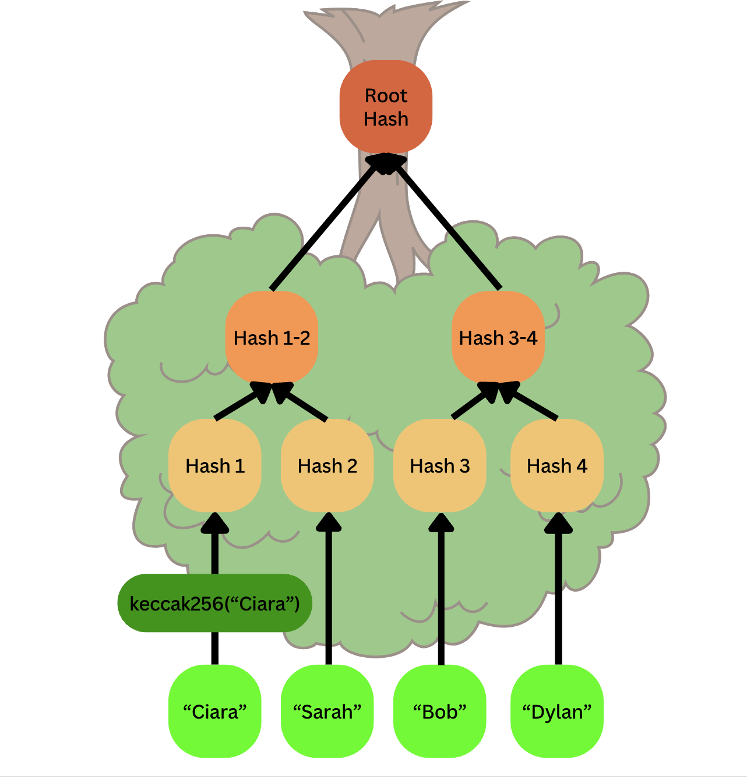
Merkle 树示意图

‍

一个叶节点是某些哈希数据，例如 VIP 示例中的字符串 “Ciara”。相邻的叶节点会被哈希在一起以生成中间节点。相邻的中间节点会递归地哈希在一起直到产生一个单一的哈希。这个哈希被称为根哈希。

Merkle 证明用于证明某些特定数据在一组数据（在 Merkle 树中）中存在。这些数据可以是任何东西，例如俱乐部 VIP 的名字，我想证明我的名字在 VIP 名单上。

Merkle 树是一个 二叉树 ，其中每个叶节点表示某些数据的哈希，每个中间节点则是其两个子节点的哈希。最上方的节点称为 Merkle 根。

‍

Merkle 树如何工作？

让我们拆解如何创建一个 Merkle 树：

1. 每条数据（字符串 “Ciara”）被哈希以生成叶节点哈希（使用像 keccak256 这样的哈希算法）：某些文本
2. Hash 1 = Hash(Data 1)
3. Hash 2 = Hash(Data 2)
4. Hash 3 = Hash(Data 3)
5. Hash 4 = Hash(Data 4)

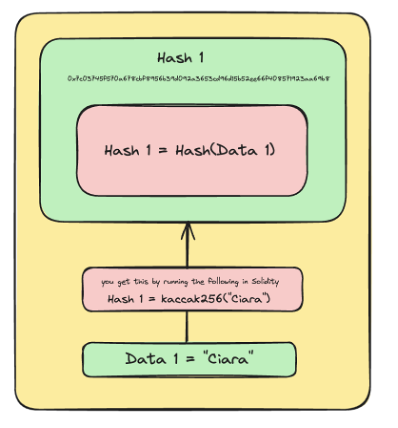
Hash 1 的图示。

1. 然后，相邻的叶节点被哈希在一起以生成中间节点：某些文本
2. Hash 1-2 = Hash(Hash 1, Hash 2)
3. Hash 3-4 = Hash(Hash 3, Hash 4)

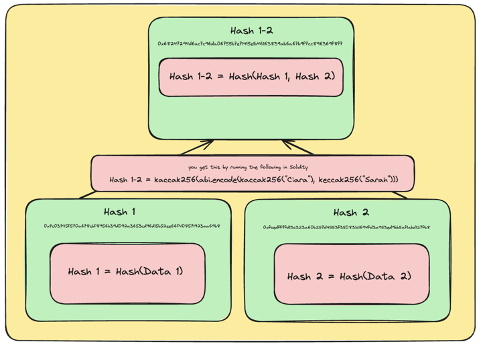
Hash 1-2 的图示。

‍

1. 相邻的中间节点随后会被哈希在一起以生成根哈希（预期的根哈希）某些文本
2. Root Hash = Hash(Hash 1-2, Hash 3-4)

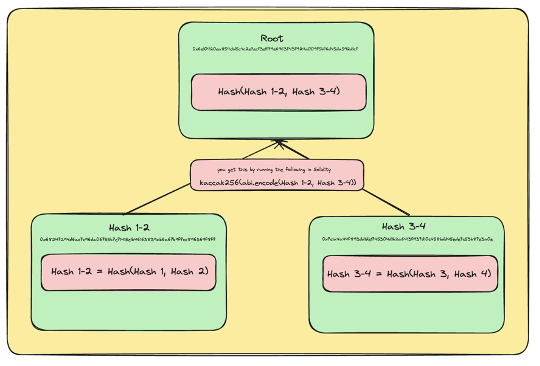
根哈希的图示。

‍

将所有这些结合在一起，我们可以将 Merkle 树可视化为：

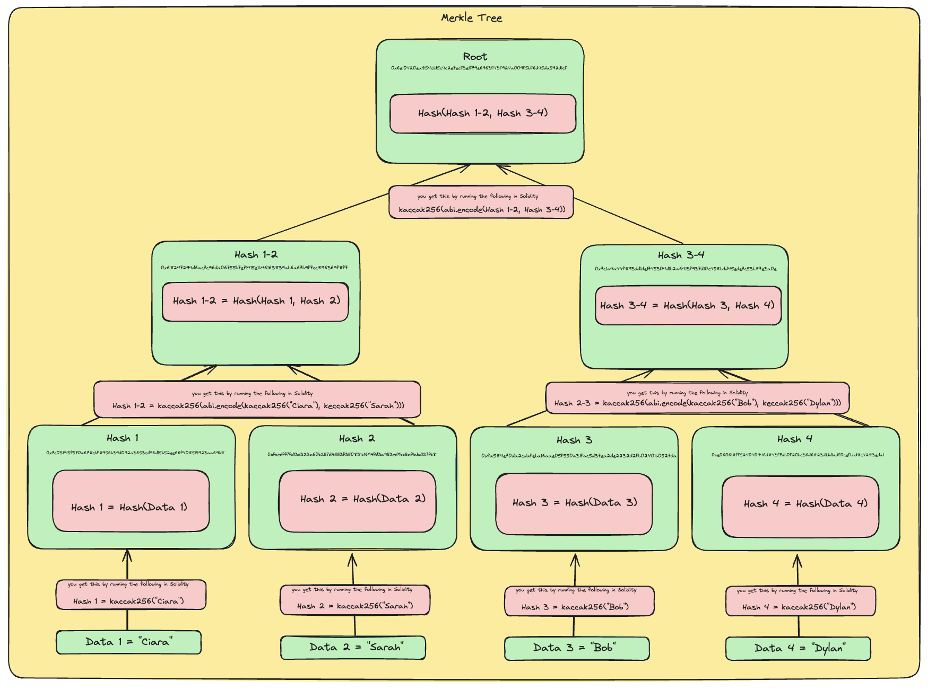
完整 Merkle 树的图示。

‍

要证明某些数据存在于 Merkle 树中–证明 “Ciara” 是 VIP 俱乐部的一部分：

1. 提供者（在我们的示例中，将是一个试图进入俱乐部的人）提供：某些文本
2. 数据，例如，在我们的 VIP 示例中，他们的名字 “Ciara.”
3. 一个数组包含所需的其他中间节点，以重构树并计算根哈希。这被称为 Merkle 证明。

所以，为了证明名字 “Ciara” 在树中，他们必须提供一个数组 Proof = [Proof 1, Proof 2]

• 其中：某些文本
  • Proof 1 = Hash 2
  • Proof 2 = Hash 3-4。

2. 然后将数据的哈希与证明的第一个元素 Proof 1 进行哈希，然后将所得的哈希与第二个元素 Proof 2 进行哈希，以生成计算得到的根哈希。在我们的 VIP 示例中，某些文本
3. Hash(“Ciara”) 与第一个证明数组元素 Hash 2 进行哈希
4. 然后该结果与第二个证明元素 Hash 3-4 进行哈希，以生成预期根哈希
5. 计算出的根哈希与预期的根哈希进行比较，以检查名字是否在树中。在我们的 VIP 示例中，只有俱乐部所有者才能访问此预期根。

使用一个安全的哈希函数如 keccak256 使得创建哈希碰撞的可能性几乎是不可能的；找到两个不同输入集得到相同哈希的可能性是如此之低，以至于在实践中不会发生。这是因为在使用 keccak256 时，该数据的哈希对于不同的数据片段是唯一的。如果在 Merkle 证明中存在匹配的根哈希，则你知道该项一定是原始根哈希计算的一部分。

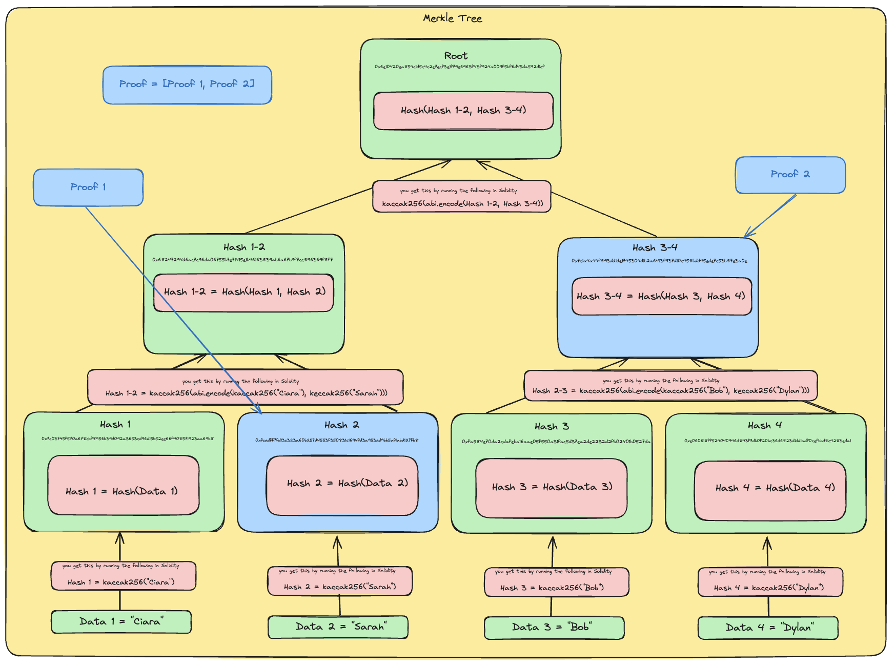
带注释的完整 Merkle 树的图示。

‍

让我们看看我们的 VIP 示例的 JSON。如下所示，你可以看到输入。这是 VIP 名单中名字的字符串。证明是重构树所需的两个中间节点；根是预期根哈希，叶是叶节点 - 输入数据的哈希，例如 keccak256(“Ciara”)。

[\
   {\
       "inputs": [\
           "Ciara"\
       ],\
       "proof": [\
           "0xfcedff7fd13c323a60b257d4553f350831c1694fd3a953ed9bb5af1abd127fb8",\
           "0x7c1a4a44f893dd1de1745304d1b2a6413f937d10c458bdd45ede7c53b87e3a0e"\
       ],\
       "root": "0x6e10420ea854c1d5c4c2e7ecf3e1f79e6963f43f924a009f5bf6d45da592d1cf",\
       "leaf": "0x7c03745f570a678cbf8956b39d092a3653cd96d15b52ee66f408571923aa69b8"\
   },\
   {\
       "inputs": [\
           "Sarah"\
       ],\
       "proof": [\
           "0x7c03745f570a678cbf8956b39d092a3653cd96d15b52ee66f408571923aa69b8",\
           "0x7c1a4a44f893dd1de1745304d1b2a6413f937d10c458bdd45ede7c53b87e3a0e"\
       ],\
       "root": "0x6e10420ea854c1d5c4c2e7ecf3e1f79e6963f43f924a009f5bf6d45da592d1cf",\
       "leaf": "0xfcedff7fd13c323a60b257d4553f350831c1694fd3a953ed9bb5af1abd127fb8"\
   },\
   {\
       "inputs": [\
           "Bob"\
       ],\
       "proof": [\
           "0xe060618ff524040946d843f7db0f20bc36d6823d1dd1adf0cefbbd8c4283eda1",\
           "0x68247294d6ac7c96da06755b7e71415e1b46163839ab6a67b9f7cc896369f8f7"\
       ],\
       "root": "0x6e10420ea854c1d5c4c2e7ecf3e1f79e6963f43f924a009f5bf6d45da592d1cf",\
       "leaf": "0xfa584e70da2cdafeba16aae05f550a31fac5d37ea2de2232d2fb02401b0527da"\
   },\
   {\
       "inputs": [\
           "Dylan"\
       ],\
       "proof": [\
           "0xfa584e70da2cdafeba16aae05f550a31fac5d37ea2de2232d2fb02401b0527da",\
           "0x68247294d6ac7c96da06755b7e71415e1b46163839ab6a67b9f7cc896369f8f7"\
       ],\
       "root": "0x6e10420ea854c1d5c4c2e7ecf3e1f79e6963f43f924a009f5bf6d45da592d1cf",\
       "leaf": "0xe060618ff524040946d843f7db0f20bc36d6823d1dd1adf0cefbbd8c4283eda1"\
   }\
]

‍

在智能合约中使用 Merkle 树

要将 Merkle 树实现到智能合约中并验证某些任意数据是否在 Merkle 树中，我们可以使用 OpenZeppelin 的 MerkleProof.sol 智能合约。让我们看看它是如何工作的：

• verify 接受证明、Merkle 根以及我们想要验证的叶节点。通常情况下，根将存储在智能合约中，证明将离线计算并作为函数调用的参数传递。
• processProof 将迭代通过证明数组中的每个元素。
• 从叶节点开始，通过与证明中的下一个元素进行哈希更新计算哈希。某些文本
  1. 哈希将始终先处理较小的值。
  2. OpenZeppelin 使用 mstore 和 keccak256 操作码进行效率优化，而不是简单地使用 keccak256(abi.encodePacked(a, b))。
• 计算出的哈希将被返回，并与预期根进行比较，以确定提供的叶节点是否存在于 Merkle 树中。

function verify(bytes32[] memory proof, bytes32 root, bytes32 leaf) internal pure returns (bool) {
    return processProof(proof, leaf) == root;
}

function processProof(bytes32[] memory proof, bytes32 leaf) internal pure returns (bytes32) {
    bytes32 computedHash = leaf;
    for (uint256 i = 0; i < proof.length; i++) {
        computedHash = _hashPair(computedHash, proof[i]);
    }
    return computedHash;
}

function _hashPair(bytes32 a, bytes32 b) private pure returns (bytes32) {
    return a < b ? _efficientHash(a, b) : _efficientHash(b, a);
}

function _efficientHash(bytes32 a, bytes32 b) private pure returns (bytes32 value) {
    /// @solidity memory-safe-assembly
    assembly {
        mstore(0x00, a)
        mstore(0x20, b)
        value := keccak256(0x00, 0x40)
    }
}

‍

有关如何使用 OpenZeppelin 的 MerkleProof.sol 智能合约的示例，请查看 MinimalMerkle 示例仓库。

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.24;

import {MerkleProof} from "@openzeppelin/contracts/utils/cryptography/MerkleProof.sol";

contract MinimalMerkle {
   bytes32 immutable public i_root;

   error MinimalMerkle__NotInClub();

   constructor(bytes32 _root) {
       i_root = _root;
   }

   function verifyIfInClub(string memory name, bytes32[] memory proof) public view returns (bool) {
       bytes32 leaf = keccak256(bytes.concat(keccak256(abi.encode(name))));

       if (!MerkleProof.verify(proof, i_root, leaf)) {
           revert MinimalMerkle__NotInClub();
       }

       return true;
   }
}

‍

生成 Merkle 树和第二前像攻击

可以使用两个主要库生成 Merkle 树：

• OpenZeppelin 的 JavaScript 库
• DMFXYZ 的 Murky Solidity 脚本

这两个库都将输入数据哈希两次，以防止所谓的第二前像攻击。

在第二前像攻击中，一个中间节点作为叶节点呈现，因此通过了检查，因为它在 Merkle 树中存在。

如果函数接受 62 字节的叶子作为输入，则此情况是可能的。这意味着攻击者可以将两个哈希合并的叶节点哈希作为输入（在哈希之前），这被称为中间节点的前像，而不是其哈希值。由于 Solidity 中的哈希长度为 32 字节，因此编码两个叶节点哈希的结果将是 64 字节。

通过不接受 64 字节长的叶节点数据和/或对叶节点使用与中间哈希不同的哈希函数，这种情况得到了缓解。这可以通过对数据进行两次哈希来实现，类似于使用不同的哈希函数。中间哈希则只通过哈希一次。当我们使用这两个脚本来生成 Merkle 树时，生成的 Merkle 树抵抗前像攻击，因为用于生成叶节点的数据已哈希两次。

有关更多信息，Rareskills 发布了一篇关于 第二前像攻击 的精彩文章。

‍

现实世界中的 Merkle 用例

空投

与使用地址的数组或映射相比，Merkle 树可以在空投智能合约中使用，以提高性能并减少索赔的 gás 成本。

Merkle 树用于高效空投，以安全且可验证的方式向大量接收者分发代币，而无需在链上存储整个接收者名单。在此过程中，合格接收者及其相应的代币分配被哈希以创建 Merkle 树中的叶节点。然后，根被发布在链上，作为空投智能合约的一部分。每个接收者可以通过提供离线计算的 Merkle 证明来索取他们的代币。

区块链

区块头包含有关区块本身的信息，并包含以下字段：

• 交易根： 交易树的 Merkle 根的 Keccak 哈希
• 收据根： 交易收据树的 Merkle 根的 Keccak 哈希 ‍
• 状态根： 状态（执行后）树的 Merkle 根的 Keccak 哈希

这些“根”起到 Merkle 根的作用。状态、交易和收据都是编码到 Merkle Patricia 树中，根包含在区块头中！

为了简化，你可以将一个 Merkle Patricia 树 视为与 Merkle 树相同，因为根哈希是依赖于子节点的，如果任何子节点发生变化，根哈希也会变化。

更多信息，请参阅这篇 noxx EVM 深入研究文章。

汇总

汇总是一种 Layer 2 扩展解决方案，旨在增加像以太坊这样的区块链网络的吞吐量。它将多个链下交易打包，并将批次的根哈希发布到主链。下面是 Merkle 树在汇总中的使用方式：

• 批次根： 交易被捆绑并编码为使用 Merkle 树的单个根哈希。批次根包含批次中的所有交易。要证明交易是否包含在批次中，需要提供交易细节、批次根和证明包含路径的 Merkle 证明。
• 状态根： 汇总的前后状态变化（之前和新的批次状态）被表示为 Merkle 树，称为状态树，状态根提交在 layer 1 链上。

这些根随后被发布在 layer 1 链上，使用 Merkle 证明验证特定交易或状态，证明其在汇总中的包含。

‍

总结

Merkle 树是一种数据结构，通过迭代地将相邻的任意数据片段哈希在一起，创建一个单一节点——称为 Merkle 根——其中包含关于树中所有子节点的信息。然后使用 Merkle 证明来证明是否某些任意数据存在于树中。

Merkle 树在高效的空投、存储区块链交易、收据和状态数据以及在汇总中整合和证明批次和状态数据方面非常有用。

• 原文链接： cyfrin.io/blog/what-is-a...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～