Solidity定点库中的问题——Certora漏洞披露

Solidity 定点库中的问题 — Certora Bug Disclosure

作者：Netanel Rubin-Blaier。

编辑：Uri Kirstein，Yura Sherman。

背景

在计算机科学中，定点表示 是一种通过存储其小数部分的固定位数（即小数点右侧的位数）来表示实数的方法。 显然，操作定点数对于任何 DeFi 应用程序都至关重要，例如，计算利率、借款指数、确定 AMM 价格曲线等。

也许不太明显的是，即使是很小的舍入或实现错误也可能累积和复合，从而可能导致套利机会甚至安全漏洞。 最近的例子包括：

• Alpha Homora 漏洞（2021 年 2 月）
• Solana 程序库中的 spl-token-lending bug（2021 年 12 月）
• Yieldly HDL 分配池 漏洞（2022 年 3 月）
• Hundred Finance 漏洞（2023 年 4 月）
• Midas Capital 漏洞（2023 年 6 月）

另请参阅 ERC-4626（Tokenized Vaults）中关于“安全考虑”的部分，该部分建议在计算 vault shares 时使用不同的、相反的舍入方向。

在 Solidity 中实现高级数学函数的两个优秀资源是 Mikhail Vladimirov 的 Math in Solidity 博客系列，以及 Remco Bloeman 的 网站。 后者激发了 Solidity 中最受欢迎、gas 效率最高且最复杂的定点库之一 — 由 Paul Razvan Berg 编写的 PRBMath 库。 总的来说，该库编写和维护得非常好，包括对其各种功能的多个单元测试。 但是，使用 Equivalence Checker，我们最近发现了 PRBMath 库中一个以前未知的设计缺陷，该缺陷会影响以下函数：

function mulDivSigned(int256 x, int256 y, int256 denominator) pure
returns (int256 result)
/// @notice Calculates floor(x*y÷denominator) with full precision.
/// @notice 以全精度计算 floor(x*y÷denominator)。

问题很简单，但是当在 DeFi 环境中实施时，它可能导致严重漏洞和资金损失。 它存在于每个 PRBMath 库实例中，版本号从 1.1.0 到 4.0（含 4.0）。

据我们所知，这是自动工具首次在公共、开源的 Solidity 库中发现错误。

错误的描述

粗略地说，PRBMath 用于计算有符号乘法和除法的算法可以分为三个步骤 —

1. 提取输入的符号和绝对值：

• (abs_x,abs_y,abs_d) := (x,y,d) 的绝对值
• (sign_x,sign_y,sign_d) := (x,y,d) 的符号

// Get hold of the absolute values of x, y and the denominator.
// 获取 x、y 和分母的绝对值。
uint256 xAbs;
uint256 yAbs;
uint256 dAbs;
unchecked {
  xAbs = x < 0 ? uint256(-x) : uint256(x);
  yAbs = y < 0 ? uint256(-y) : uint256(y);
  dAbs = denominator < 0 ? uint256(-denominator) : uint256(denominator);
}
// Get the signs of x, y and the denominator.
// 获取 x、y 和分母的符号。
uint256 sx;
uint256 sy;
uint256 sd;
// "sgt" is the "signed greater than" assembly instruction and "sub(0,1)" is -1 in two's complement.
// “sgt”是“有符号大于”汇编指令，“sub(0,1)”是二进制补码中的 -1。
assembly ("memory-safe") {
  sx := sgt(x, sub(0, 1))
  sy := sgt(y, sub(0, 1))
  sd := sgt(denominator, sub(0, 1))
}

2. 通过减少到无符号情况来计算结果的绝对值：

uint256 abs_result = mulDiv(abs_x, abs_y, abs_d);

其中

function mulDiv(uint256 x, uint256 y, uint256 denominator) pure
returns (uint256 result)
/// @notice Calculates floor(x*y÷denominator) with full precision.
/// @notice 以全精度计算 floor(x*y÷denominator)。

3. 计算总符号并返回结果：

uint256 overall_sign = sign_x ^ sign_y ^ sign_d;
result = (overall_sign == 0) ? -int256(abs_result) : int256(abs_result);

问题在于步骤 2 是错误的。 我们实际上有：

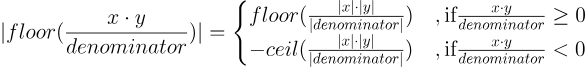
所以无论何时结果为负数，我们实际上都是向零而不是负无穷舍入，从而导致相差一的错误。

影响和正确的披露程序

在处理项目时，审计师通常根据严重性（错误可能造成的损害程度：拒绝服务、资金损失……）和难度（恶意行为者将漏洞 weaponize 成实际利用的难度）对智能合约错误进行分类。

我们首先遇到这个错误是在处理领先的 DeFi 协议之一的未发布 AMM¹ 代码时，该代码使用 mulDivSigned 作为其 交易函数 计算的一部分。 在某些情况下，这种算术错误会使攻击者能够迫使流动性池接受不利交易²，系统地耗尽 LP 代币的价值。

最初，我们将此漏洞归类为严重级别，但难度也很高，并通知了客户，客户已在其代码中修复了该问题。 但是，当我们注意到这种算术错误发生在 PRBMath 库的多个实例中，因此可能会影响更多系统（包括实时系统）时，我们的初始分类变得复杂。

这带来了一个难题：即使在“经典”计算机安全领域，库错误也臭名昭著地危险，并且很难跨项目估计严重性和难度。 这种难度在以太坊中更加复杂，以太坊缺乏对可升级库的本机支持或用于分发热修复的机制，并且（出于 gas 原因）人们更喜欢直接从 PRBMath 复制特定函数并对其进行调整，而不是导入整个库。

在咨询了领先的安全研究人员 samczsun 和 Mudit Gupta 之后，我们彻底搜索了公共存储库（链上和链下），并私下通知了潜在的易受攻击项目。 我们还联系了 Paul Razvan Berg（PRBMath 的作者），他立即与我们进行了通话并确认了调查结果。

根据我们的调查，我们认为目前很少有智能合约以有问题的方式使用 PRBMath 的有符号算术部分。 因此，考虑到智能合约的不可变性质，最好将其公开。

缓解措施

为了快速解决问题，Paul 发布了一个临时修复程序（版本 4.1），该程序将 mulDivSigned 的定义更改为向零舍入：

function mulDiv(uint256 x, uint256 y, uint256 denominator) pure
returns (uint256 result)
/// @notice Calculates x*y÷denominator with 512-bit precision.
/// @notice 使用 512 位精度计算 x*y÷denominator。
/// Notes:
/// 注意：
/// - The result is rounded toward zero.
/// - 结果向零舍入。

从长远来看，作为正在进行的计划的一部分，这个问题将得到长期的解决方案，以便在 PRBMath 中为多个舍入模式提供广泛的支持，请参阅 此处 的讨论以了解更多信息。

结论

数学库是 DeFi 生态系统的基本构建块。 然而，令人惊讶的是，它们很难做对（尤其是在试图积极优化其 gas 消耗时），并且审计它们可能很乏味且困难。

上面的错误表明，即使进行了全面的单元测试，为系统编写正式规范的过程也具有巨大的方法论优势（即使只是为了确保没有任何内容被忽略或遗漏）。 它也很好地说明了 CVL 语言的可表达性 - 一个基本的 CVL 规范（“等效规范”）

能够检测到一个数学库的 Solidity 代码中一个存在了 2 年的错误，该错误涉及大量的 Yul 片段、大量的位 hacking 技巧，甚至还涉及一些数论知识 — 所有这些都不需要甚至了解实现的任何细节。

¹ 有关 DEX、AMM 和相关 DeFi 术语的快速回顾，请参阅调查论文“SoK：具有自动做市商 (AMM) 协议的去中心化交易所 (DEX)”。

² 也称为 AMM 或 CFMM 不变量。

• 原文链接： medium.com/certora/probl...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～