格密码学进阶之一：Lattice Trapdoors（格中陷门）

本文作者东泽，来自安比技术社区的小伙伴，目前就读于斯坦福大学，研究方向密码学。

写在前面

前一段时间写完基于格的GSW全同态加密系统（FHE）后，笔者对格产生了很大的兴趣。由于上学期在学校上的CS355（高阶密码学）讲完FHE之后就结课了，所以还有很多关于格的知识没有讲到。

正如开学的时候CS355第一节课上说的一样：对于其他专业的学生来说，这会是你们密码学方向学习的最后一节课。但是对于密码学方向的人来说，这将会是你们真正入门密码学的第一节课。

这节课结束之后，后面就没有系统性的课程了。在过去的两个月内，为了更加全面的学习格密码学，笔者只好去网上与各个学校搜刮讲座和课件，拼凑起来从头开始学习Lattice的基础定义和几大难题。对于格有一个大致的了解之后，就可以看懂更加进阶的东西，比如IBE、ABE、NIZK、Multilinear Map、iO等等。了解完一圈下来，不得不说格密码学真的是万能的一个密码学分支，可以基本上实现所有密码学的应用（Crypto-Complete）。

关于Lattice-based Crypto的入门知识，有兴趣的大家可以去看笔者的【Lattice学习笔记】这一专题。在这里就假设大家对格已经有一个大致的了解了。从这一期开始，我们开一个新的专题【格密码学进阶】，学习一下更加进阶的格密码学的算法和构造。

这一期，我们来看看格密码学中的一个非常重要的工具：Trapdoor Functions（陷门函数）。

Trapdoor Function（陷门函数）简介

Trapdoor Function（TDF），即陷门函数，是一个密码学中非常常见的一个基础工具。简单的概括一下的话，TDF就是一个普通的函数$f: D \rightarrow R$，即输入空间为$D$，输出空间为$R$。这个函数有两个非常重要的特性：

1. 首先，如果只知道这个函数的本身，那么这个函数就是一个单向函数（OWF）。单向函数是什么意思呢，就是给定一个输入$x$，我们可以非常快速（efficient）地计算$f(x)$。但是如果我们只能看到这个函数的输出$f(x)$的话，我们很难从这个值推算出原本输入$x$的值来。
2. 虽然OWF的定义在密码学应用上很有用了（比如可以构造出PRG、PRF、Hash Function等等），但是TDF更加特殊的属性是，在生成一个TDF实例的时候，我们会额外生成一个这个函数的一个Trapdoor $t$。如果不知道Trapdoor $t$的值，那么原本的TDF仍然是一个OWF。但是如果一旦有人知道了Trapdoor $t$，那么就可以直接打破单向性，即可以有效的从$f(x)$中还原回$x$出来。

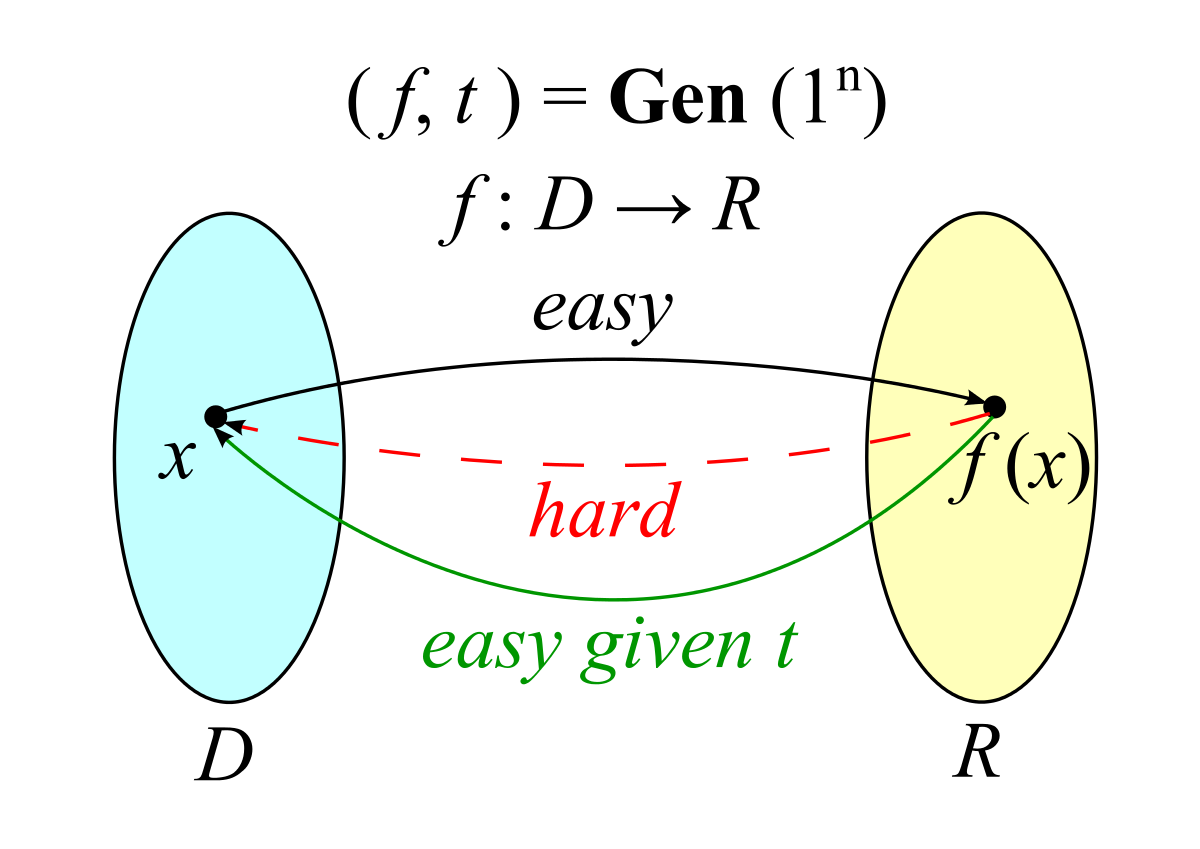
Wikipedia上对于TDF使用了上述的一张图片来解释。理解起来很简单：从$D$到$R$很容易，但是从$R$到$D$很困难。但是如果知道了Trapdoor $t$，那么从$R$到$D$也会非常简单。

TDF在密码学上的应用多不胜数，比如我们最常见的RSA加密算法就基于RSA的一个TDF。在RSA一开始的密钥生成的过程中，我们会生成一对加密和解密的密钥$(e, d)$。我们可以基于这一对密钥来定义RSA的TDF： $$ f{RSA}(m) = m^e \text{ mod }N\ f{RSA}^{-1}(c) = c^d \text{ mod }N\ f{RSA}^{-1}(f{RSA}(m)) = (m^e)^d = m \text{ mod }N $$ 因为大整数的有限域（$\text{mod }N$）中，已知$m^e$的话，我们很难还原出一开始的$m$。但是如果我们知道了这个系统的Trapdoor $t = d$的话，那么我们就可以直接计算$m^{ed}$然后还原出最初的$m$来。

其他的TDF也是类似的样子，我们在生成这个OWF函数实例的时候预先预留好一个“后门”，即Trapdoor，然后知道这个后门的人就可以轻松的打破单向性。

如果我们要把TDF的概念带到格中来的话，首先我们需要来看看，Lattice当中我们都知道哪些OWF的构造。

SIS与LWE的OWF结构

看过前面的一系列文章（尤其是Lattice学习笔记）的朋友们应该对此不太陌生了。这里我们再来重新回顾一下Lattice中的两大难题：Short Integer Solution（SIS）与Learning With Errors（LWE）。

基于SIS的单向函数$f_\mathbf{A}$

首先我们先看SIS问题。

SIS相对来说结构比较简单，我们需要随机生成一个矩阵$\mathbf{A} \in \mathbb{Z}q^{n \times m}$作为公开的部分。然后SIS问题就是，给定$\mathbf{A}$，能否找到一个“短向量”$\mathbf{x} \in \mathbb{Z}{{0, \pm1}}^m$（一般来说为了方便计算，我们会把短向量定义为每个维度都是一个bit的向量），使得： $$ \mathbf{Ax} = 0 \text{ mod }q $$ 这样一个求解短向量的问题（即SIS），在格密码学中被公认是一个困难的问题。同理，我们可以根据SIS的难度来构造一个OWF $f_\mathbf{A}$: $$ \mathbf{A} \in \mathbb{Z}q^{n \times m}: f\mathbf{A}(\mathbf{x}) = \mathbf{Ax} \text{ mod }q $$ 我们得到的这个函数$f\mathbf{A}$被Ajtai在1996年被证明为是一个单向函数（OWF）。具体的证明可以参考【Lattice学习笔记】中的对应内容，简单的说就是求解$f\mathbf{A}^{-1}$可以被规约到在Lattice $\Lambda(\mathbf{A})$的对偶格中求解CVP问题，而CVP又是另一个公认的格中难题。

在选择$f\mathbf{A}$的参数的时候，我们一般会把$q$压的比较小，使得这个OWF是一个满射（surjective）的函数，这代表了会有多个不同的短向量$\mathbf{x}, \mathbf{y}$，使得： $$ f\mathbf{A}(\mathbf{x}) = f_\mathbf{A}(\mathbf{y}) $$ 这一满射的特性决定了SIS OWF一定会有碰撞（Collision）的存在。但是这个OWF还有另一个特殊的属性：它是抵抗碰撞的（Collision Resistant）。这代表了就算这个OWF存在碰撞，我们也无法有效的根据一个已知的$\mathbf{x}$，找到另一个对应的$\mathbf{y}$来。

基于LWE的单向函数$g_\mathbf{A}$

接下来我们看格中另一个难题，LWE。LWE问题具体的我们在之前的文章中很详细的描述过了，这里我们就跳过介绍直接讲定义。

一个LWE问题实例包含了一个随机生成的矩阵$\mathbf{A} \in \mathbb{Z}_q^{n \times m}$，一个随机生成的向量$\mathbf{s} \in \mathbb{Z}_q^m$，还有一个错误分布区间$\mathcal{X}_B$。一般为了方便理解，我们会把$\mathbf{A}$拆分为$n$个随机生成的向量$\mathbf{a_1, \dots, a_n}$来看待。

简短的概括LWE问题的话，那么就是带有噪音的内积问题。假设有一个未知的向量$\mathbf{s}$，我们的目标是猜出这个向量的值来。LWE问题给了我们一系列的随机向量$\mathbf{a}_1, \dots, \mathbf{a}_n$，并且还给我们看这些向量和未知向量$\mathbf{s}$的带噪音内积： $$ \mathbf{b}_i \leftarrow \langle \mathbf{a}_i, \mathbf{s} \rangle + \mathbf{e}_i :\mathbf{e}_i \in \mathcal{X}_B $$ 其中的噪音部分就是从噪音分布中随机选取的。我们一共可以看到$n$格内积的值。如果用矩阵的方式来表示的话： $$ \mathbf{b} = \mathbf{As} + \mathbf{e} $$ 如果给定了$\mathbf{A}$和一组有噪音的内积$\mathbf{b}$的话，LWE问题定义了从$\mathbf{A, b}$中还原出原本的位置向量$\mathbf{s}$是困难的。

和上面的SIS一样，基于这个问题的困难性，我们可以开发出一个新的OWF出来： $$ g_\mathbf{A}(\mathbf{s}, \mathbf{e}) = \mathbf{s}^t \mathbf{A} + \mathbf{e}^t \in \mathbb{Z}_q^m $$ 这个OWF的输出其实就是LWE中的$\mathbf{b}$本身了。因为LWE是困难的，所以我们就算看到了$\mathbf{A}, \mathbf{b}$，我们也不能推算出这个OWF的输入$\mathbf{s}, \mathbf{e}$来。所以根据LWE的困难度，我们就可以定义这个OWF的单向性了。相比起上面SIS需要依靠CVP问题的规约来完成证明，LWE的安全性证明简单了不少。

LWE OWF的一个特性在于它是单射（injective）的。和满射不同，所有的LWE问题（只要各项参数选择符合要求）都有一个唯一的解。

$f\mathbf{A}$与$g\mathbf{A}$的反函数与Preimage Sampleable Function（PSF）

了解完基于SIS的OWF $f\mathbf{A}$和基于LWE的OWF $g\mathbf{A}$之后，我们现在来尝试引入Trapdoor的概念。

首先，我们先不要着急想Trapdoor到底是个啥。是个向量还是矩阵还是数字并不重要。我们先思考一下， 假如我们已经拥有了这么一个神奇的Trapdoor，我们可以做什么。

现在我们的$f\mathbf{A}$和$g\mathbf{A}$已经满足了单向性的属性，即我们可以快速的计算这个函数，但是无法从函数的输出结果有效地还原出输入来。根据前面对于TDF的描述，如果我们已知了Trapdoor，那么理应我们就可以构造出这个OWF的反函数来。这样的话，上面描述的两种OWF构成的反函数$f\mathbf{A}^{-1}, g\mathbf{A}^{-1}$分别会是什么样子的呢？

基于LWE的$g\mathbf{A}$的反函数最简单，因为它是单射的（即每个输出都有一个唯一的输入解），所以$g\mathbf{A}^{-1}$会输出唯一的一对满足条件的输入$\mathbf{s}, \mathbf{e}$。

基于SIS的$f\mathbf{A}$就不太一样了，因为这个函数是满射的（即碰撞存在），所以$f\mathbf{A}^{-1}$应该会在所有满足条件的答案中，随机选择输出的一个$\mathbf{x'}$。在安全性的考虑上，这个“随机选择”的过程必须要是一个高斯分布，并且反函数输出的$\mathbf{x}'$应该需要和输入空间$\mathbb{Z}_{{0, \pm1}}^m$中符合要求的解的分布大致相同。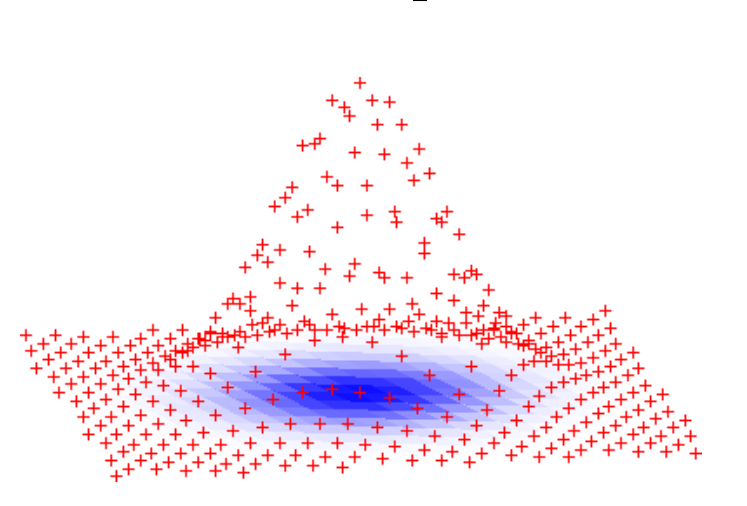

上面的图就是Micciancio和Peikert在MP12这篇paper中对于$f\mathbf{A}^{-1}$的输出空间分布的一个大概的描绘。在MP12中，他们把满足这类分布的一对满射函数与其反函数$f\mathbf{A}, f_\mathbf{A}^{-1}$称作为Preimage Sampleable Function（PSF）。

具体是什么意思呢？其实很简单，这就是在说我们使用$f\mathbf{A}$和$f\mathbf{A}^{-1}$可以生成同样的一组概率分布。

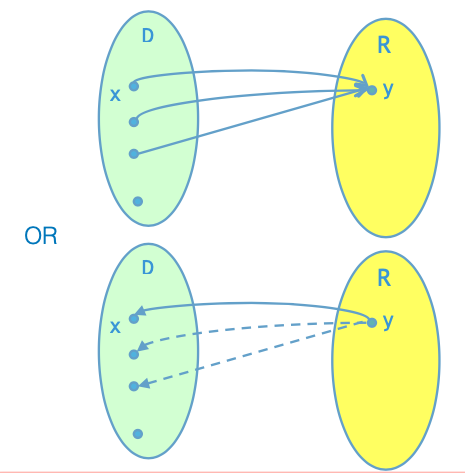
如同图上所绘，我们首先使用$f\mathbf{A}$：我们在$\mathbb{Z}{{0, \pm1}}^m$中抽取高斯分布的随机向量，然后统计下来所有通过$f_\mathbf{A}(\cdot)$之后结果等于一个任意选择的向量$\mathbf{y}$的向量$\mathbf{x, x', x'', \dots}$。

随后，我们使用$f\mathbf{A}^{-1}$：我们随机的选择一个输出空间中的向量$\mathbf{y}$，然后使用$f\mathbf{A}^{-1}(\mathbf{y})$这个反函数来还原一系列符合要求的输入$\mathbf{x, x', x'', \dots}$。

PSF的定义就是，我们使用上述两种方法生成的$\mathbf{y, x, x', x', \dots}$在概率上的分布是computationally相同的。也就是说，如果我们看到一组符合分布要求的$\mathbf{y, x, x', x', \dots}$，我们无法分辨这组随机的向量组合到底是选定随机的输入通过$f\mathbf{A}$生成的，还是选定随机的输出通过$f\mathbf{A}^{-1}$生成的。

这个概念现在看起来可能比较晦涩，但是PSF的定义对于后续的构造十分有用，尤其是在证明基于格的NIZK的零知识属性上极为重要。这里留做一个悬念，等我们学完前序的内容后，再回来详细的研究这一点。

构造Trapdoor：第一类陷门（Type 1 Lattice Trapdoor）

当我们了解完Lattice中最有名的两大OWF和他们对应的理想中的反函数的大致构造（和输入输出分布）之后，我们就可以开始实战构造Trapdoor了。

系统性的分类的话，Lattice Trapdoor大致分为两种。我们首先着重了解一下第一种：基于Lattice的几何构造形成的Trapdoor。

基向量的好坏

如果我们随机的生成一个Lattice（如上图所示），虽然格点是固定的，但是我们可以选取不同的基向量（basis vector）来描述这个Lattice。

一组代表了Lattice结构的基向量，其实具有好坏之分。好的基向量（good basis）可以让我们非常直观的求解很多格中的问题。然而坏的基向量（bad basis）则反之。

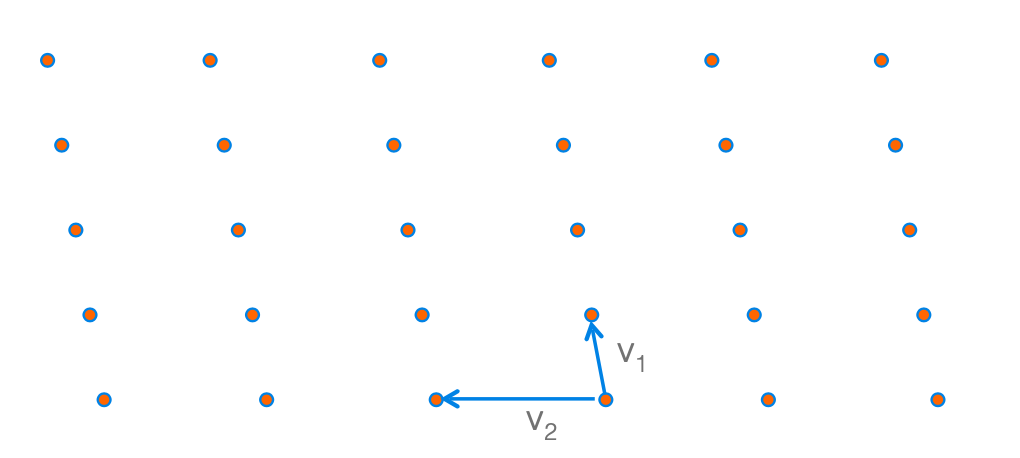
我们首先选出这个格中最好的一组基向量$\mathbf{v}_1, \mathbf{v}_2$。我们发现，这一组向量很短，并且几乎是相互垂直的。这两个属性代表了这一组基向量构成的Determinant的基础空间（Parallelpiped）具有近似于长方体的形状。

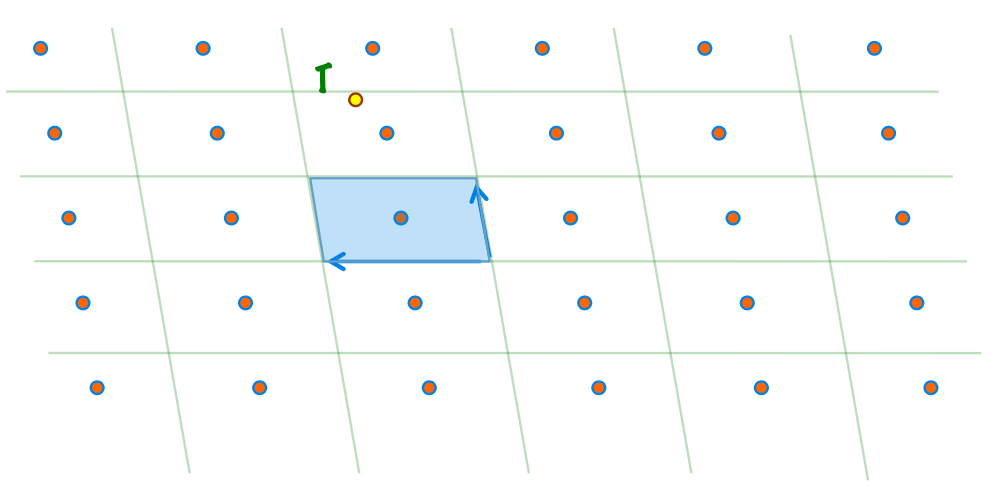
在这种结构内，求解CVP问题是很简单的。假如我们拥有一个$\mathbb{R}^n$的任意的点$\mathbf{t}$，要找到距离这个点最近的格点$\mathbf{v} \in \Lambda(\mathbf{v}_1, \mathbf{v}_2)$，我们只需要看这个点到底在哪一个长方体（Parallelpiped）内，然后直接输出这个长方体中心对应的格点就可以了。

现在我们来看坏基的大致结构。

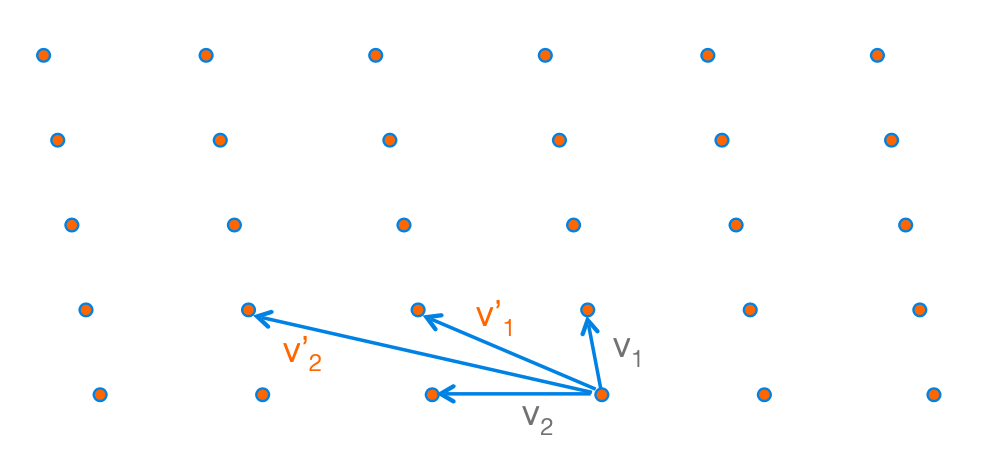
我们可以选择两个不同的基向量$\mathbf{v}_1', \mathbf{v}_2'$作为这个Lattice的新的基。这一组基就没有之前的结构那么的完美：基向量之间靠的距离很近，并且长度也很长。

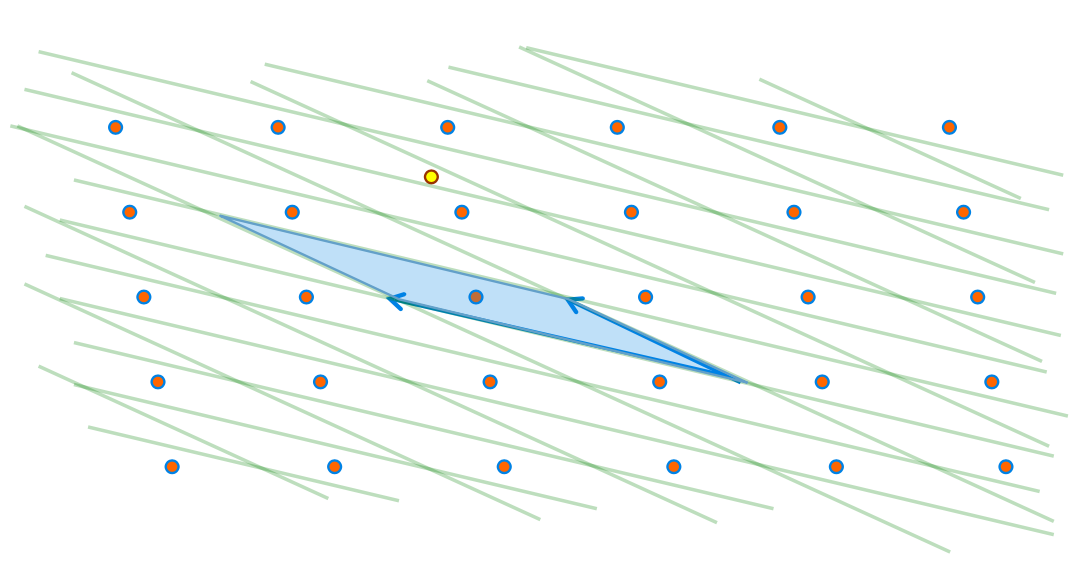
现在我们基于这一组坏的基组成的Parallelpiped分割一下多维空间。我们会发现这些平行多面体的形状非常的狭长，所以上面描述的CVP的解法就不管用了。

比如说图中距离黄点最近的格点就是在它右下方的红点，但是这个黄点却坐落在它左上角的红点代表的Parallelpiped上。所以如果我们直接用上述的方法来解CVP的话，那么很大可能性我们会找错点，找到并不是最近的那个格点上。

基向量好坏的不对称性

基于我们上面的观察，我们可以发现Lattice系统中的一个不对称性：

如果给定了一组坏的基（bad basis），那么在这个基的格中的SVP、CVP、SIS等常见问题都是困难的。但是反之，如果我们给了一组好的基（简短、近似垂直），这些格中的问题就会变得非常好解决。

我们都知道，如果一个数学系统出现了如上的不对称性的话，那么我们就可以把这一特性拿来用做密码学。这也就是第一类格陷门的精髓了。

这也就是说，对于一个Lattice $\Lambda$来说，我们可以尝试找到两种表述方式：

1. 第一种方式就是一个随机的矩阵$\mathbf{A}$，也就是一组随机的（坏的）基。基于这个矩阵，我们可以轻松的通过线性组合这些基向量来构造出格点，但是无法从格点还原回我们原本的线性组合来。
2. 第二种方式就是一个短矩阵$\mathbf{A}_\text{short}$，这个矩阵就是一组近似相互垂直并且短的（好的）基。基于这个矩阵，我们就可以快速的把格点拆分回原本的线性组合，甚至是求解一些格中困难的问题，比如SVP、CVP等等。

对于$g\mathbf{A}$来说，我们可以通过$\mathbf{A}\text{short}$来快速的求解CVP然后找出$\mathbf{s}$。同理，对于$f_\mathbf{A}$来说，这一组短的基可以帮助我们成功的找到一组均匀高斯分布的$\mathbf{x}, \mathbf{x}', \mathbf{x}'', \dots$。

Type 1 Trapdoor的问题

第一类格陷门基于几何上的特点，所以非常好理解。然而，给定一个随机选择的$\mathbf{A}$的话，到底该如何生成$\mathbf{A}_\text{short}$呢？这个问题在几何上就很难找到答案了。

所以一般来说，Type 1的格陷门是为了方便、强化我们对于Trapdoor的理解而存在的，但是构造Type 1的格陷门相对来说比较困难。虽然当我们得到了对应的$\mathbf{A}\text{short}$之后，我们就可以很简单的计算$f\mathbf{A}^{-1}, g_\mathbf{A}^{-1}$，但是实际使用中，我们不会使用这一类的陷门。

下一期：第二类格陷门（Type 2 Lattice Trapdoor）

了解完Type 1 Trapdoor之后，想必大家对于Lattice TDF的大致构造和工作方式应该有了个大概的了解了。然而，Type 1的问题在于这个Trapdoor矩阵$\mathbf{A}_\text{short}$的构造并不简单，所以对于我们真正构造使用Lattice TDF没有太大的帮助。

MP12这一篇paper中，主要描述了他们构造的新一类的Trapdoor，即Type 2 Trapdoor。这一类的Trapdoor虽然并不是像Type 1一样的一组短的基向量，但是Type 2的Trapdoor和Type 1一样强大（可以轻松的构造反函数），并且更加高效。

更加神奇的是，当我们拥有Type 2 Trapdoor之后，我们可以利用这个Trapdoor来构造Type 1 Trapdoor需要的短向量矩阵$\mathbf{A}_\text{short}$。所以等我们学会Type 2的构造之后，我们可以回头再看看Type 1是如何生成的。

由于篇幅原因，这一期就说到这里啦。我们下期再见。

References

本文内容主要参考于IIT Madras的教授Shweta Agrawal的讲座。