格密码学进阶之三:基于格的Identity-based Encryption(身份加密)
- 安比实验室
- 发布于 2020-09-28 14:41
- 阅读 8138
斯坦福学霸笔记之格密码学进阶(三)
上期回顾
上一期,我们了解了Lattice Trapdoor的具体构造。基于Trapdoor,我们可以有效的逆向计算基于SIS与LWE的两个单向函数$f\mathbf{A}, g\mathbf{A}$。
我们再来快速的回顾一下Lattice Trapdoor的构造。
首先,我们需要选择一个Uniform Random的矩阵$\mathbf{B} \in \mathbb{Z}_q^{n \times m'}$,然后再选择一个高斯分布的短矩阵$\mathbf{R} \in \mathbb{Z}q^{m' \times n \log{q}}$。随后,我们就可以构造我们的问题矩阵$\mathbf{A}$: $$ \mathbf{A} = [\mathbf{B} \vert \mathbf{G - BR}] $$ 这个矩阵对应的Trapdoor就是矩阵$\mathbf{R}$了,因为我们可以通过$\mathbf{R}$来把$\mathbf{A}$转换到到工具矩阵$\mathbf{G}$上: $$ \mathbf{A} \cdot \begin{bmatrix}\mathbf{R}\\mathbf{I}\end{bmatrix} = \mathbf{G} $$ 通过这个构造,我们就可以把基于$\mathbf{A}$的单向函数问题$f\mathbf{A}, g\mathbf{A}$转换为基于$\mathbf{G}$的单向函数问题$f\mathbf{G}, g\mathbf{G}$。因为工具矩阵$\mathbf{G}$的结构公开已知,所以我们可以很轻易的求解$f\mathbf{G}^{-1}, g\mathbf{G}^{-1}$从而计算$f\mathbf{A}^{-1}, g_\mathbf{A}^{-1}$。
Lattice Trapdoor的构造非常简单,设计也很巧妙。接下来,这一期我们来看看基于Lattice Trapdoor最直观的应用:身份加密(IBE)。
身份加密(Identity-based Encryption,IBE)
IBE的概念想必大家之前也有所耳闻,具体的在这篇文章中就不多解释了,在zhihu上有很多其他大佬对于IBE系统给出了非常详细的解读。
在这里我们给出一个很简单的解读方式:IBE就是一个可以任意选择公钥的公钥加密系统。
具体是什么意思呢?基于Diffie-Hellman的ElGamal公钥加密系统我们都知道,需要提前经过密钥生成(KeyGen)的阶段才能生成一对乱码一样的公钥和私钥。随后我们把公钥公布出来之后,其他人就可以通过公钥加密了。这样的系统虽然可行,但是当网上需要公钥加密的人越来越多之后,难免会遇到很大的问题:每个人都有属于自己的一串乱码公钥,如果想要和任何其他人通讯,就必须要记住别人的公钥。
像这样的所有人都记住所有人的公钥的系统,我们称之为PKI(Public Key Infrastructure)。PKI的缺点就在于当人数越来越多的时候,整个系统就变得非常没有效率,公钥的存储成本非常大。
IBE想要解决的问题就是,如果Alice给Bob发消息,并不需要提前记住Bob的公钥,而是直接把消息加密在Bob的名字下面。当Bob解密的时候,他只需要他证明他是Bob本人,就可以解开密文看到原文了。
为了保证这个IBE系统能够正常的运作,我们还需要一些额外的定义。首先,一个群体需要有一个信任的管理员,这个管理员拥有整个群体的万能公钥(MPK)和万能私钥(MSK)。管理员可以通过MSK来给每个人签发基于每个人名字的私钥$SK{ID}$,同时公布MPK给所有人看。当Alice给Bob发消息的时候,她会基于MPK和Bob的ID("Bob")创建密文。随后Bob就可以通过他专属的$SK\text{Bob}$来解密。这样的话,所有人只需要记住MPK和接收消息的人的ID,就可以安全的交换消息了。
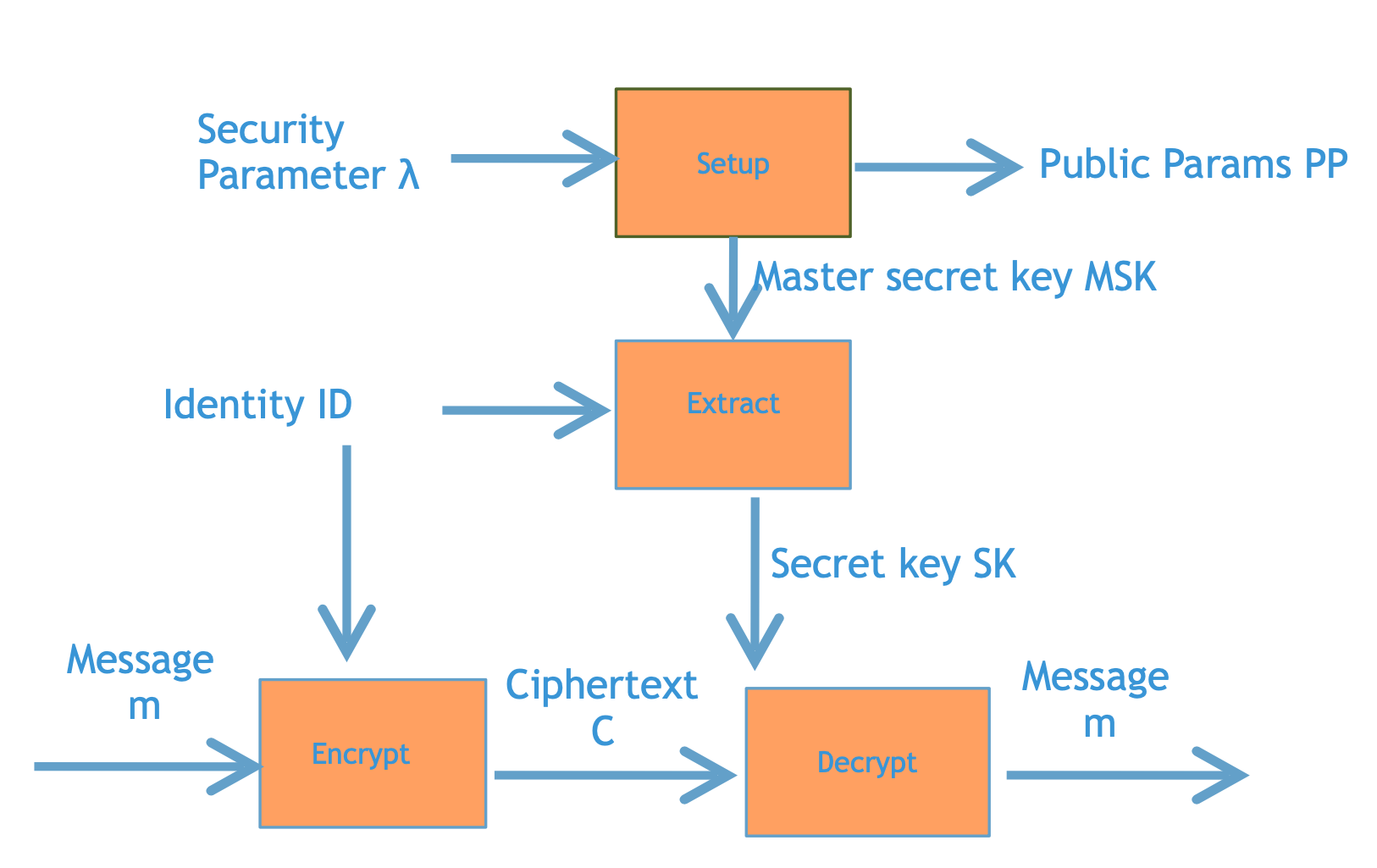
如果放到一张图上来说的话,大概就像上图所述。我们可以看到,一个IBE系统就是把对方的ID作为了加密的时候使用的公钥。对应的在解密的时候,我们通过MSK和ID提取出专门的密钥$SK_{ID}$进行解密。
IBE是一个相对来说比较老的密码学构造了,在将近20年前被提出,并且基于双线性配对已经有了很好的构造。这一期,我们就来看看如何使用Lattice Trapdoor来构造这个系统。
Regev加密系统回顾
首先,我们需要回顾一下Regev Encryption加密系统。我们这里的IBE构造,精髓就基于Regev Encryption的一个变种。
如果大家看过我之前的【初探全同态加密】系列的话,那应该会对基于LWE的Regev加密系统有一定的了解。我们在这里快速的回顾一下:
- $KeyGen$:首先,我们需要创建一个LWE的问题实例,即创建一个问题矩阵$\mathbf{A}$,然后随机选择一个密钥$\mathbf{s}$和噪音$\mathbf{e}$,最后我们计算$\mathbf{b = As + e}$。随后我们输出私钥$sk = \mathbf{s}$,公钥$pk = (\mathbf{A, b})$。
- $Encrypt(pk, \mu \in {0,1})$:我们加密一个bit的方式很简单,只需要随机选择一个blinding factor $\mathbf{r} \in \mathbb{Z}_2^m$,然后计算$c_0 = \mathbf{r}^t \mathbf{A}$,$c_1 = \mathbf{r}^t \mathbf{b} + \lfloor q/2 \rfloor \mu$。随后我们输出密文为$(c_0, c_1)$。
- $Decrypt(sk, ct=(c_0, c_1))$:如果要解密的话,我们只需要计算$c_1 - c_0 \cdot \mathbf{s} = \mathbf{r}^t \mathbf{e} + \lfloor q/2 \rfloor \mu$。因为噪音向量的分布我们控制的很小,所以我们可以直接通过观察结果的值是否小于$q/4$来判断$\mu$是0还是1。
具体的Regev加密的正确性和安全性,可以参见【初探全同态加密】这一专题。
我们之前学到的Regev Encryption的精髓在于,因为LWE问题的困难度,我们可以安全的把密文$x$隐藏在一个看似随机的向量$\mathbf{b}$中。然而作为密钥生成方我们知道LWE问题的解,所以我们可以很轻松的从密文中移除$\mathbf{b}$这一项,剩下原本的原文和一些小范围的噪音。
如果看过【Lattice学习笔记】,想必大家都会知道,既然有基于LWE的系统出现,那么肯定就会有基于LWE的小兄弟——SIS的系统出现。我们能否把这个Regev加密系统转化成基于SIS难度的系统呢?
Gentry,Peikert与Vaikuntanathan在08年的论文GPV08中,对于Regev的加密体系进行了一个细小的变换,得到了一个基于SIS难度的系统——Dual Regev加密系统。具体方案如下:
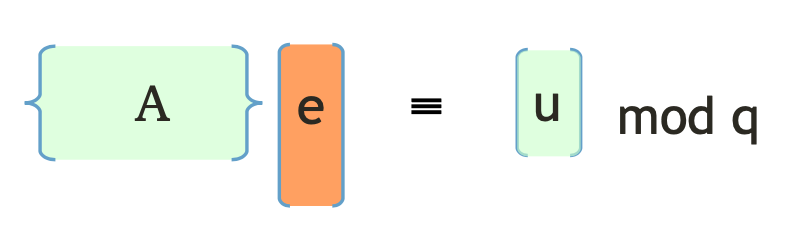
- $KeyGen$:因为Regev的密钥生成是生成一个LWE的实例,我们这里想必就要生成一个SIS的实例了。如同上图所述,我们选取随机的$\mathbf{A}$,和密钥短向量$\mathbf{e}$,计算$\mathbf{u = Ae} \text{ mod }q$。随后我们输出私钥$sk = \mathbf{e}$,公钥$pk=(\mathbf{A, u})$。
- $Encrypt(pk, \mu)$:我们选取一个随机的LWE问题的解$\mathbf{s}$,噪音向量$\mathbf{x}$,和一个单独的噪音值$x$。然后我们计算$c_0 = \mathbf{A}^t \mathbf{s} + \mathbf{x}$,$c_1 = \mathbf{u}^t \mathbf{s} + x + \lfloor q/2 \rfloor \mu$。随后输出$(c_0, c_1)$。
- $Decrypt(sk, ct=(c_0, c_1))$:解密和之前是一样的,我们计算$c_1 - \mathbf{e}^t c_0 = \lfloor q/2 \rfloor \mu + x - \mathbf{e}^t \mathbf{x}$。由于后两项都为噪音分布空间中很小的值,所以我们可以很简单的提取出原文$\mu$来。
Dual Regev模式的精髓在于,在密钥生成的阶段,我们不会生成任何LWE的实例,而这个实例是在加密的过程中被随机选择出来的。相比起Regev是在密钥生成阶段就锁定了唯一的一个LWE实例,而在加密阶段选择一个随机的向量$\mathbf{r}$来增加随机性。
Dual Regev模式的好处在于它的公钥部分$(\mathbf{A, u})$是纯平均随机分布的。因为我们随机的挑选了平均分布的$\mathbf{A}$,并且选择了高斯分布的$\mathbf{e}$,我们知道$\mathbf{u}$一定是呈平均随机分布的!相比起普通Regev模式下的公钥$(\mathbf{A, b})$作为LWE的问题实例,$\mathbf{b}$并不是平均随机分布的!虽然在DLWE假设中,我们假设$(\mathbf{A, b})$是computationally和平均分布相似的,但是在statistical(概率分布)的层面上,$\mathbf{b}$并不是Uniform的。
关于Dual Regev公钥的平均分布看起来没什么用,但是对于IBE系统来说至关重要。为什么这么说呢?这是因为IBE系统中我们要求任何ID都可以当作加密使用的公钥,然而这一特性Dual Regev下公钥的平均随机分布正好是完美契合的,这对于之后的安全性证明帮助非常大。
基于Dual Regev的IBE架构
了解完Dual Regev的具体构造之后,接下来我们就可以尝试基于它来实现IBE了。
我们知道一个IBE系统下,我们需要可以把任意的ID当作公钥进行加密。所以我们需要想办法在密文和密钥中“嵌入”这么个ID的值进去。
在了解怎么做之前,我们再来看一下Dual Regev的精髓在哪里。
我们在选择Dual Regev系统的密钥的时候,就像之前的图上所述,我们需要先选择一个关键的SIS问题实例,即一组$\mathbf{A, e, u}$: $$ \mathbf{Ae} = \mathbf{u} \text{ mod }q $$ 然后我们可以对着这个SIS问题的题面,即$\mathbf{A, u}$进行Regev公钥加密。随后可以根据这个SIS问题的解$\mathbf{e}$,对密文再进行解密。这也就是说,Dual Regev的核心就在于这个SIS问题和它的解。
我们可以把这个idea延伸到IBE上来。如果任何人可以根据要加密的对象的ID来构造一个SIS的问题矩阵$\mathbf{F}{ID}$,那么他们就可以基于这个$\mathbf{F}{ID}$和任意挑选的一个$\mathbf{u}$来进行Dual Regev加密。接下来我们只要搞清楚,拥有ID的这个人如何掌握这么个密钥$\mathbf{e}$使得SIS等式成立,就大功告成了。
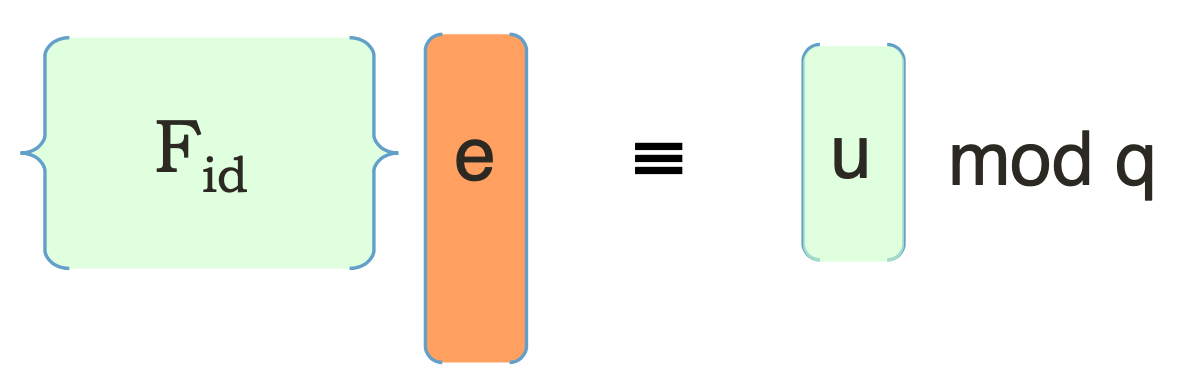
把这个问题用图描述出来,我们发现,其实这种思路的IBE就是把原本随机生成的SIS矩阵$\mathbf{A}$替换成了一个任何人可以efficiently生成的这么一个IBE矩阵$\mathbf{F}_{ID}$罢了。
由于普通的Dual Regev中,我们都是随意的挑选$\mathbf{A}, \mathbf{e}$然后再计算$\mathbf{u}$的,现在我们反了过来:提前计算好了$\mathbf{u}$,并且任何人都可以生成固定的$\mathbf{F}_{ID}$,那么我们怎么才能让拥有ID的人得到一个有效的$\mathbf{e}$满足SIS呢?
是不是非常的有即视感?这个时候,就需要轮到我们的Lattice Trapdoor出场了。
我们上一期学到的Trapdoor,告诉我们我们可以构造一个看似随机的$\mathbf{A}$,但是自带一个“后门”$\mathbf{R}$,让我们可以有效的计算基于$\mathbf{A}$的SIS/LWE单向函数的反函数。这里我们当然也要构造这么一个$\mathbf{A}$,并且想办法嵌入到我们的$\mathbf{F}_{ID}$中。嵌入的方法不同,最后得到的IBE也不同。
下面我们就来看看第一种IBE体系——CHKP10 IBE加密系统。
【CHKP10】IBE加密系统
Cash,Hofheinz,Kitz和Peikert在2010年发表的CHKP10中,给出了一个非常优雅的基于Lattice的IBE构造,我们来看看是怎么实现的。
ID的选择
首先,即然说到了IBE,我们就要先来看看这个ID到底是什么东西。如果Alice想要给Bob发送消息的话,那么这个ID就是一个字符串“Bob”。如果在学校里给别的同学发消息的话,那么这个ID很有可能就是收件人的学号,等等。
因为ID这里有很多种含义,为了方便我们IBE系统的构造,我们就定义ID为一个长度为$l$的二进制字串。因为我们可以把任何字符串或者编号转换为二进制,所以只需要解决二进制下的ID,就等于解决了所有IBE的应用了。
在这里,为了方便我们对于IBE系统的展示和运算,我们定义ID就是一个2 bits的一个数字: $$ \lvert ID \rvert = 2\ ID \in \mathbb{Z}_2^2 $$
公共参数生成
一个IBE系统的第一步就是生成它的公共参数了,即生成我们上文所述的MPK与MSK。
在CHKP10中,我们首先需要使用我们上一期讲到的Trapdoor的方法,生成一个带有Trapdoor $\mathbf{R}$的随机矩阵$\mathbf{A}_0$。随后,对于ID的每一个bit,我们都生成两个随机矩阵$\mathbf{A}_i^0, \mathbf{A}_i^1$。最后,我们再随机选取一个看得顺眼的$\mathbf{u}$,就搞定了。

图上所述的就是当ID为两位的时候,我们一共需要生成6个关键元素:带陷门的$\mathbf{A}_0$,对应每一位随机生成的$\mathbf{A}_1^0, \mathbf{A}_1^1, \mathbf{A}_2^0, \mathbf{A}_2^1$,和一个向量$\mathbf{u}$。
这6个关键元素,就是我们IBE系统的MPK了。同时,$\mathbf{A}_0$的Trapdoor $\mathbf{R}$,就是这个系统的MSK。
生成ID矩阵
当我们进行加密的时候,首先我们需要根据加密的ID计算出对应的$\mathbf{F}_{ID}$以便我们进行Dual Regev加密。当我们拿到了上面生成的公共参数之后,就可以把这些参数根据对应的ID的值组合起来,就可以构成$\mathbf{F}$了。我们举个例子,如果我们加密选择的ID是01的话,那么我们就可以把$\mathbf{A}_0$矩阵和对应每一个bit的$\mathbf{A}i^b$拼接起来: $$ \mathbf{F}{ID} = [\mathbf{A_0} \vert \mathbf{A_1^0} \vert \mathbf{A}2^1] $$ 这样一来,最后会得到一个长条形的$\mathbf{F}{ID}$,我们随后就可以通过它来使用Dual Regev进行IBE加密了。
但是到这里还没有结束。我们知道,Dual Regev的精髓在于我们需要提前知道一个短的密钥$\mathbf{e}$,使得$\mathbf{Ae} = \mathbf{u} \text{ mod }q$。这里也一样,我们需要找到对应的$\mathbf{e}$使得: $$ \mathbf{F}_{01} \mathbf{e} = [\mathbf{A}_0 \vert \mathbf{A}_1^0 \vert \mathbf{A}_2^1] \mathbf{e} = \mathbf{u} \text{ mod }q $$
使用Lattice Trapdoor计算密钥
接下来,我们需要计算出这个ID对应的密钥$\mathbf{e}$。
首先,我们已知了$\mathbf{A}_0$这个矩阵的Trapdoor $\mathbf{R}$,同时其他的两个矩阵$\mathbf{A}_1^0, \mathbf{A}_2^1$是随机生成的。这也就是说,我们需要找到一个长矩阵,并且满足: $$ [\mathbf{A_0} \vert \mathbf{A_1^0} \vert \mathbf{A}_2^1] \begin{bmatrix} \mathbf{a}\ \mathbf{b}\ \mathbf{c} \end{bmatrix} = \mathbf{u} \text{ mod }q $$ 我们需要求解的就是这$\mathbf{a, b, c}$三个部分。解决方案十分简单:我们随机的选择$\mathbf{b}$和$\mathbf{c}$的值,使得整个等式变成: $$ \mathbf{A}_0 \cdot \mathbf{a} = \mathbf{u} - [\mathbf{A_1^0} \vert \mathbf{A}_2^1] \begin{bmatrix} \mathbf{b}\ \mathbf{c} \end{bmatrix} \text{ mod }q $$ 这样一来,求解$\mathbf{a}$就变成了计算基于$\mathbf{A}0$的SIS OWF的反向函数。我们只要使用$\mathbf{R}$来构造$f{\mathbf{A}_0}^{-1}$,然后再计算出$\mathbf{a}$就大功告成。最后,我们输出对应于这个ID的IBE密钥: $$ \mathbf{e} = \begin{bmatrix} \mathbf{a}\ \mathbf{b}\ \mathbf{c} \end{bmatrix} $$ 真正在使用场景中,整个群组中拥有MSK的管理员会计算出这个$\mathbf{e}$并且发给ID为01的人。这样一来这个人就可以解开所有发给01的密文了。
IBE加密
当我们成功的构建$\mathbf{F}_{01}$之后,就可以进行Dual Regev加密了。由于之前讲过了,这里就快速的带过。 $$ Enc(\mu \in {0,1}, ID=01) \rightarrow \ (c0 = \mathbf{F}{01}^t \mathbf{s} + \mathbf{x}, c_1 = \mathbf{u}^t \mathbf{s} + x + \lfloor q/2 \rfloor \mu) $$ 和之前的构造相同,我们选取随机的向量$\mathbf{s}$,和对应的噪音$\mathbf{x}, x$以便完成加密。
IBE解密
解密和之前也是一样的,ID为01的人就可以通过$\mathbf{e}$来计算: $$ c_1 - \mathbf{e}^t c_0 = \lfloor q/2 \rfloor \mu + x - \mathbf{e}^t \mathbf{x} \approx \lfloor q/2 \rfloor \mu $$
CHKP10的安全性论证
以上就是CHKP10的IBE加密体系的全貌了!接下来是最重要的部分,即安全性论证(Security Proof)。
一般讨论类似于IBE一样的加密系统的话,我们的安全性论证一般都会使用一个security game来描述。在这个game中我们作为Challenger,我们的任务是尝试去“挑战”解决一个公认的难题,比如LWE。随后,在这个game中还存在着一个Adversary,它的目标是尝试攻破我们描述的IBE系统。然后整个game可以被描述为,Challenger把想要解决的LWE难题包装成一个IBE的系统,然后让Adversary去尝试攻破它。我们把IBE的构造设置为,如果Adversary可以有效的攻破它,那么我们就可以利用Adversary输出的结果来解决我们想要解决的LWE问题。
这其实就是变相地说,我们可以把LWE问题伪装成一个IBE,进而证明我们提出的IBE的系统的安全性。因为如果这个系统可以被攻破,那么就代表它对应的LWE问题也能被攻破。
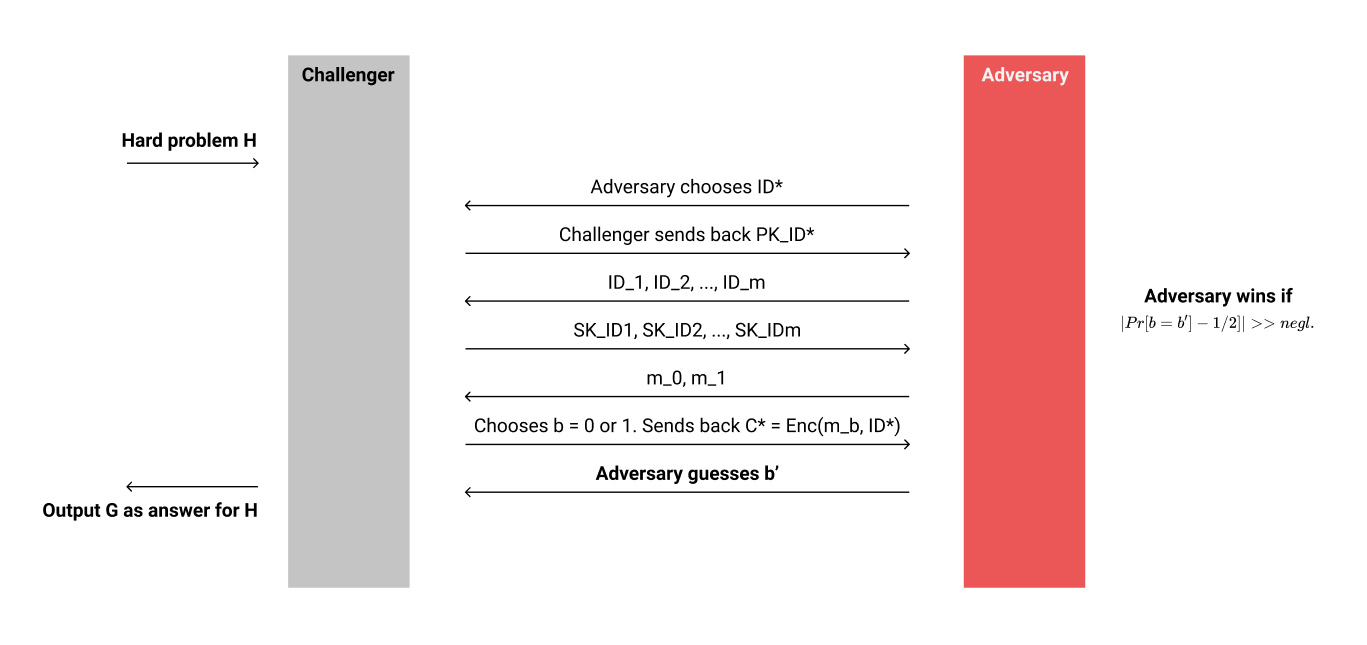
简单的画了个图描述了一下整个security game的大致流程。
- 首先,Challenger会接收到一个困难的问题实例,比如LWE。
- 随后开始IBE系统的构造。我们作为Challenger需要能够回答来自Adversary的一些问题。第一类问题是公钥问题,即Adversary提供任意的ID,我们需要返回过去对应这个ID的IBE加密矩阵$\mathbf{F}_{ID}$。在这类问题中,Adversary需要决定一个它想要破解的ID,即$ID^*$。
- 第二类问题就是密钥问题(Key Queries)。这个过程中,Adversary可以任意的选择合理的ID,只要并不是$ID^*$,我们就要回答对应这个ID的私钥$SK_{ID}$。
- 在Adversary问完问题结束之后,我们的security game进入了最后的阶段。Adversary选择并且提供两段长度相同的密文$m_0, m_1$,然后发送给Challenger。随后Challenger会随机选择一个bit $b \in {0,1}$,然后基于$b$的值构造密文$C^ = Enc(m_b, ID^)$,并且把密文发送给Adversary。
- Adversary需要基于密文,判断并输出$b' \in {0,1}$,尝试猜出我们选择的$b$的值。
- 最后,我们根据Adversary给出的答案,尝试解决一开始得到的困难问题。
由于篇幅原因,我们不会构建完整的一套security game,而是着重于focus在Challenger与Adversary的交互上。观察这个game当中的交互之后,可以总结出几点关键。
IBE安全证明的关键点
首先,第一点我们已经提到过了,就是作为Challenger本身,我们需要能够回答Adversary提出的密钥问题。这也就是说,我们需要有能力可以创建对应的$\mathbf{F}_{ID}$的Trapdoor。
但是需要注意的是,因为我们的目的是为了解决一个困难问题(比如SIS/LWE),所以我们需要把这个问题嵌入到security game当中来。放到IBE的场景中来的话,比较可行的方式就是:我们只能生成一部分(Adversary选择的)ID的密钥。但是对于Adversary一开始决定的$ID^$,我们使用输入进来的困难问题作为它的公钥。这样一来,如果Advesary可以破解基于$ID^$下的Dual Regev的话,那么代表我们也可以利用Adversary来破解构造它的困难问题了。
这一构造意味着什么呢?这代表我们作为Challenger本身并不能知道$ID^*$的密钥。这也间接的要求了我们不能知道整个IBE系统的MSK。但是我们又需要在不知道MSK的情况下任意的构造出Adversary提出的任意其他ID对应的密钥。
在这样的构造下,如果我们可以在不知道MSK和$ID^$的前提下,成功的回答Adversary提出的各种问题,这就意味着这个IBE系统中,除了$ID^$之外的其他ID的加密解密流程,我们就算不知道$SK_{ID^*}$,也可以完全simulate(模拟)出来。
说到模拟的概念,了解零知识的朋友都不陌生了。假如我不知道$SK{ID^*}$,也可以完全模拟出IBE系统里其他ID的transcript(交互信息)的话,那就代表其他的ID下的加密解密的transcript对于$SK{ID^*}$这一消息来说是零知识的!
IBE Transcript Simulation
现在我们的问题明确了:我们需要在不知道$ID^$的前提下,构造其他的ID的密钥,并且仍然保留IBE的正确性。此外,我们还可以基于已知的困难问题,构造一个困难的密文$C^$发给Adversary。
接下来,我们就来看一看构造吧。为了方便演示,我们假设$ID^* = 11$。
首先,因为构造要求,我们知道我们不可能会知道$SK_{ID^}$,这也就代表了我们并不知道MSK,即$\mathbf{A}_0$的Trapdoor。其次,我们想使得$ID^$下的所有密文都基于困难的SIS/LWE问题。基于这两条要求,我们可以随机的选取$\mathbf{A}_0, \mathbf{A}_1^1, \mathbf{A}_2^1$,并且确保这三个矩阵是纯随机的(没有Trapdoor的存在)。
这样一来,我们来看看基于$\mathbf{F}{ID^*}$的IBE加密矩阵: $$ \mathbf{F}{ID^} = [\mathbf{A}_0 \vert \mathbf{A}_1^1 \vert \mathbf{A}2^1] $$ 由于这三个矩阵都是没有Trapdoor的,所以$\mathbf{F}{ID^}$也是没有Trapdoor的。如果Adversary可以破解基于$\mathbf{F}{ID^*}$的Dual Regev,这也就代表它可以破解基于$\mathbf{F}{ID^*}$的SIS/LWE啦。
实现了困难问题这一要求之后,我们再来看一看密钥问题(Key Queries)。为了能够成功的生成其他ID下的SK,解决的方法很简单:我们只需要生成带有Trapdoor的$\mathbf{A}_1^0, \mathbf{A}2^0$就行了。原理很简单,只要我们的$\mathbf{F}{SK}$的构造中有任何一个带有Trapdoor的矩阵,那我们就可以生成整个SK啦。举个例子: $$ \mathbf{F}_{01} = [\mathbf{A}_0 \vert \mathbf{A}_1^0 \vert \mathbf{A}_2^1] $$ 我们可以就利用$\mathbf{A}1^0$的Trapdoor来生成$SK{01}$。
这就是CHKP10 IBE的安全性论证的全貌了。我们回顾一下,整个证明的核心在于两点:
- 我们可以在不知道$SK{ID^*}$的情况下生成其他所有ID的密钥。这代表了就算知道了其他所有ID的密钥,我们也不能还原出$SK{ID^*}$。
- 我们把$ID^*$下的IBE公钥变成了一个纯随机生成(没有Trapdoor)的SIS/LWE矩阵。这样如果存在可以破解我们IBE security game密文的Adversary,我们就可以利用这个Adversary来攻破SIS/LWE。
Q.E.D.
写在篇尾
这一期,我们了解了基于Lattice构造(尤其是Lattice Trapdoor)下的身份加密(IBE)体系。
稍微总结一下这一期的内容:首先我们了解了IBE大概的定义,并且看到了帮助我们构造IBE的Dual Regev加密系统。随后我们看到了CHKP10提出的IBE的结构,随后在最后面我们看到了这一结构的安全证明和对应的security game。
CHKP10下的IBE,虽然构造非常优雅,但是我们不禁会发现一个弊端:用于加密的矩阵$\mathbf{F}_{ID}$太长了。
我们观察可以发现,现在$\mathbf{F}{ID}$的长度,和ID有多少个bits是直接挂钩的。这也就代表了,如果我们要发送消息给一个256bits的地址,我们可能需要构造一个非常非常大的$\mathbf{F}{ID}$来用作IBE加密的矩阵。这一点对于整个IBE体系的实际应用是毁灭性的。
一种对策是我们像之前讨论多项式环下的Ring-SIS/LWE一样,我们把整个问题转化到Ring中,这样可以减少一点矩阵存储和相乘运算的开支。但是在维度上来看,ID和公钥的比例仍然是$O(n)$的增长。我们能否消减这一增长的比例呢?
Agrawal,Boneh与Boyan在2010年同时提出了ABB10的格IBE构造。他们的构造的公钥大小永远都是恒定在$O(1)$的,这一点相比起CHKP10是非常大的突破。
下一期,我们就来看一看ABB10这一更加高效率的IBE构造。
References
本文内容主要参考于IIT Madras的教授Shweta Agrawal的讲座。
- 以太坊协议研究学习小组 - 2026 启动 221 浏览
- 神奇的 Zig、C 和 OpenSSL 184 浏览
- Shamir份额的魔力:BLS门限签名 451 浏览
- zkMesh:2026年1月回顾 443 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 421 浏览
- ZK 编年史:电路(第二部分) 418 浏览
- 有限域之美与力量 (以及 Zig) 513 浏览
- 扳手攻击:发生与预防 549 浏览
- zkEVM 安全性概览 627 浏览
- 基于哈希函数的签名(三):多次签名 701 浏览
- 基于哈希函数的签名(二):少量次数签名 864 浏览
- Zig 签名(Ed25519 和 ECDSA) 1221 浏览

