渐进式荷兰拍卖

概要

• 1. 介绍
• 2. 离散 GDA
  • 1. 动机
  • 2. 机制
  • 1. 计算批量购买价格
• 3. 连续 GDA
  • 1. 动机
  • 2. 机制
  • 1. 计算购买价格
• 4. 代码
• 5. 结论
• 6. 附录
  • 1. 指数价格衰减的离散 GDA 的推导
  • 2. 指数价格衰减的连续 GDA 的推导
  • 3. 脚注

1. 介绍

本文介绍了一种渐进式荷兰拍卖，1 或 GDA，这是一种能够有效销售缺乏流动性市场的资产的机制。

GDA 解决了与 TWAMM 类似的问题，但不依赖于流动性提供者愿意在资产对上进行市场交易。

GDA 的工作原理是将销售分解为一系列荷兰拍卖 (Dutch auctions)——一种从高要价开始，逐渐降低，直到买家出价的拍卖类型。 GDA 允许你一次性购买多个此类拍卖，且具有 gas 效率。

我们为离散 GDA（用于销售 NFT）和连续 GDA（用于销售同质化代币）都提供了方案。我们还包括一个 Python notebook，用于建模该机制的行为，以及一个 参考 Solidity 实现。

2. 离散 GDA

1. 动机

想象一下，Alice 想要出售 10,000 个 NFT 的集合。她不确定她的艺术品的公平价格是多少，所以她不想以固定价格出售它们。

相反，她可能会选择在一次荷兰拍卖中出售所有这些 NFT——从高要价开始，然后逐渐降低，直到所有 NFT 都售出。但是，这样的拍卖可能不是最优的：可能没有足够的买家有兴趣同时购买所有作品。

相反，Alice 可以一次拍卖一个 NFT。例如，她可能会每分钟为她的系列中的一件新作品启动一个新的荷兰拍卖。这将使市场有更多时间为她的艺术品找到一个公平的价格。

离散 GDA 是这种想法的延伸，但由于其数学特性，支持批量购买多个子拍卖，且具有 gas 效率。

2. 机制

离散 GDA 适用于销售 NFT，因为这些 NFT 必须以整数数量出售。 它们的工作原理是为每个被出售的代币举行一次虚拟荷兰拍卖。 这些拍卖的行为与常规荷兰拍卖完全一样，并且能够有效地结算批量拍卖。

在离散 GDA 中，每个拍卖都同时开始，每个后续拍卖都有更高的起拍价。 每次拍卖的价格由价格函数给出，

$p_n(t)$

其中 $n$ 是拍卖的索引，并且 $t$ 是自其开始以来的时间。

各种价格函数可用于 GDA。 一种特别表现良好的公式由以下公式给出：

$p_n(t) = k \cdot \alpha^ne^{- \lambda t}$

在这里，每次拍卖的价格都根据某个衰减常数

$\lambda$

呈指数衰减。 每次拍卖的起拍价都会增加一个固定的比例因子 $\alpha$ 。 第一次拍卖的起拍价由初始价格 $k$ 给出。

1. 计算批量购买价格

给定上述价格函数，我们可以高效地计算批量购买拍卖的成本。

假设 Bob 想要购买某些数量

$q$

的代币。 为此，他将购买 $q$ 个最便宜的拍卖。 如果自拍卖开始以来已经过去了 $T$ 秒，并且到目前为止已经售出了 $m$ 个 NFT，则购买 $q$ 个代币的总价格 $P$ 由下式给出：

$P(q) = \sum_{n=m}^{m + q - 1} p_n(T)$

对于上述价格函数的情况，

$P(q)$

可以有效地计算。 如附录所示， $P(q)$ 的公式为：

$P(q) = \frac{k \alpha^m(\alpha^{q} - 1)}{e^{\lambda T}(\alpha -1)}$

我们可以绘制在单个订单中购买的代币数量与其累计价格的关系图，以获得下图：

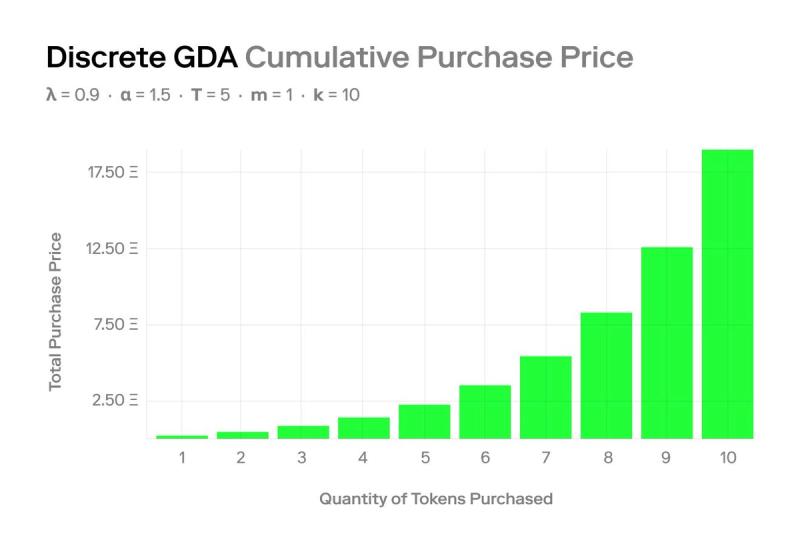
3. 连续 GDA

1. 动机

卖掉了她的 NFT 之后，Alice 现在可能想卖掉一些同质化代币。 一种选择是让她使用上面描述的离散 GDA 机制，以固定大小的批次出售她的代币。

但是，Alice 可能不想像离散 GDA 那样立即提供所有代币进行销售。 例如，她可能正在运行一个以某个恒定速率（例如，每天 360 个代币）出售排放物的协议。

她可以选择不使用离散 GDA，而是选择在一系列标准荷兰拍卖中出售她的代币。 她可以每天运行一次 360 个代币的拍卖，每小时运行一次 15 个代币的拍卖，或者每分钟运行一次 0.25 个代币的拍卖。 同样，基于她持有的拍卖数量，价格影响和 gas 效率之间存在权衡。

连续 GDA 的工作原理是将此过程推向极限，其中拍卖之间的时间间隔接近 0。这意味着销售被分成无限序列的拍卖，每次拍卖都出售数量极小的代币。

事实证明，我们仍然可以以 gas 高效的方式计算任何数量代币的购买价格。

2. 机制

连续 GDA 的工作原理是以恒定的排放率，

$r$

逐步提供更多资产以供出售。 例如，就像我们上面说的那样，Alice 可能对每分钟出售 0.25 个代币感兴趣。

排放物被分解为无限系列的虚拟拍卖。 这些拍卖会随着时间的推移以均匀的速度开始，每次拍卖都以相同的价格开始。

每次拍卖的价格由价格函数给出，

$p(t)$

其中 $t$ 是自其开始以来的时间。 就像在离散 GDA 中一样，可以使用许多不同的价格函数。 一种这样的函数是：

$p(t) = k \cdot e^{- \lambda t}$

与前面的示例一样，价格根据某个衰减常数

$\lambda$

呈指数衰减，而 $k$ 控制起始价格。

1. 计算购买价格

假设 Bob 想要购买某个数量

$q$

的 Alice 出售的代币。 为了购买那么多代币，他需要购买在一段时间内开始的每次拍卖，时长为 $\frac{q}{r}$ 秒。 由于价格随着时间的推移而降低，因此他对最旧的可用拍卖进行出价。

如果最旧的可用拍卖已经有

$T$

秒了，则购买

$q$

个代币的总价格 $P$ 由下式给出：

$P(q) = \int^{T}_{T-\frac{q}{r}} p(t)dt$

这意味着只要计算价格函数的积分成本低廉，我们就可以以 gas 高效的方式计算总购买价格。

使用上述价格函数购买

$q$

个代币的总价格可以在链上有效地计算。 如附录所示，此价格由下式给出：

$P(q) =\frac{k}{\lambda} \cdot \frac{e^{\frac{\lambda q}{r}}-1}{e^{\lambda T}}$

由此我们得到以下价格曲线：

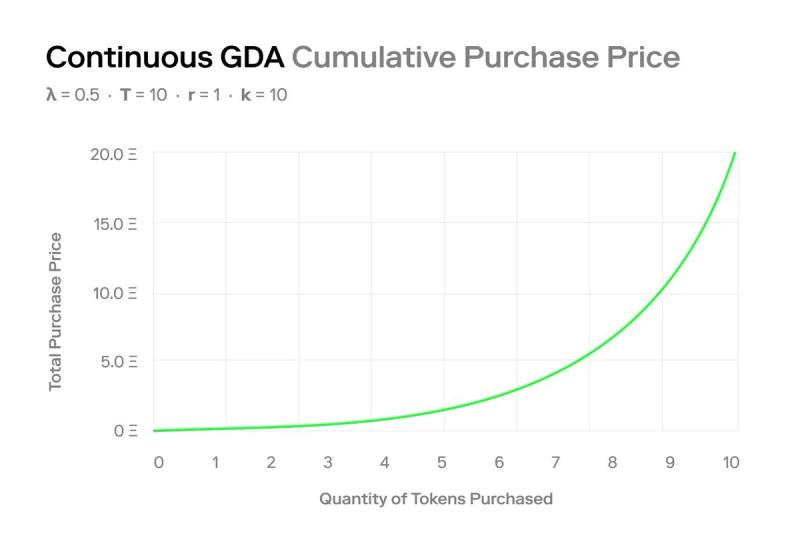
4. 代码

我们提供了一个 用于建模 GDA 的 Python notebook 和一个 参考 Solidity 实现。

5. 结论

GDA 是一种用于销售缺乏流动性市场的同质化和非同质化代币的有用机制。 尽管本文推导了一些有用的价格函数，但我们相信在不同的上下文中可以使用更多价格函数。 我们希望 GDA 在本文描述的那些应用之外的各种应用中都有用。

如果你是一名对实施其中一些概念感兴趣的构建者，请通过 Twitter 与我们联系 @FrankieIsLost, @danrobinson, @_Dave__White_ @andy8052。 我们很高兴收到你的来信。

6. 附录

指数价格衰减的离散 GDA 的推导

$P(q) = \sum_{n=m}^{m + q -1} p_n(T)$

P(q) ∑n=mm+q−1k⋅αne−λt

$P(q) \sum_{n=m}^{m + q -1} k \cdot \alpha^ne^{- \lambda t}$

P(q)ke−λT∑n=mm+q−1αn

$P(q) ke^{-\lambda T}\sum_{n=m}^{m + q -1} \alpha^n$

$P(q) \frac{k \alpha^m(\alpha^{q} - 1)}{e^{\lambda T}(\alpha -1)}$

指数价格衰减的连续 GDA 的推导

$P(q) = \int^{T}_{T-\frac{q}{r}} p(t)dt$

P(q)∫T−qrTk⋅e−λtdt

$P(q) \int^{T}_{T-\frac{q}{r}} k \cdot e^{-\lambda t}dt$

$P(q) \frac{k}{\lambda}\cdot \left( e^{-\lambda(T - \frac{q}{r})} - e^{-\lambda T} \right)$

$P(q) \frac{k}{\lambda} \cdot \frac{e^{\frac{\lambda q}{r}}-1}{e^{\lambda T}}$

3. 脚注

1. 也被称为 澳大利亚拍卖。 ↩

• 原文链接： paradigm.xyz/2022/04/gda...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～