理解 BLS 签名算法

编者注：BLS 签名算法是一种可以实现签名聚合和密钥聚合的算法（即可以将多个密钥聚合成一把密钥，将多个签名聚合成一个签名）。在以太坊未来的 Casper 实现中，有非常多的验证者都要对区块签名，要保证系统的安全性，同时节约存储空间，就需要用到这类签名聚合的算法。

之前的文章中，我介绍了 Schnorr 签名算法和它的优势。现在，我来介绍下 BLS（Boneh-Lynn-Shacham）签名算法以及它相比 Schnorr 的优胜之处。

长话短说，我们已经知道：

ECDSA 签名算法已经足够胜任它的工作，但也仅限于此。它无法做签名聚合或者密钥聚合，因此只能挨个对签名进行验证。在验证多重签名的交易时，此举过于繁琐，我们需要逐个验证所有的签名及其对应的公钥，耗费大量的区块空间和交易费。

Schnorr 签名算法就好多了，它可以把一笔交易中的所有签名和公钥合并成单个签名和公钥，且合并过程不可见（无从追溯这个签名或公钥是否通过合并而来）。另外，可以一次性对合并后的签名做验证，加快了区块验证的速度。当然，该算法也有一些不足:

• 多重签名需要多次（签名者之间的）通信，这对冷钱包来说过于麻烦。
• 聚合签名算法依赖随机数生成器，而不像 ECDSA 那样可以使用指定的随机点（R）
• m-n 多重签名机制比较取巧，需要构建公钥的默克尔树。当 m 和 n 较大时，树所占空间会相当大。
• 无法把一个区块中的所有签名聚合成一个签名

BLS 签名算法可以解决以上问题。它不需要随机数生成器，可以将区块中的所有签名聚合成一个，容易实现 m-n 多重签名，也可以避免签名者之间的多余通信。除此之外，BLS 签名的长度更短（签名为椭圆曲线上的一个点而非两个），是 Schnorr 或 ECDSA 的 2 分之一。听起来完美！那么让我们看看 BLS 签名算法的工作原理。

BLS 签名算法的魔力

进入正题前，我们先来了解两个基础概念，曲线哈希（hashingto the curve，或译作 “哈希成曲线上的点”）和曲线配对（curves pairing）。

曲线哈希

在 ECDSA 和 Schnorr 签名算法中，我们对消息进行哈希计算后，结果（哈希值）是数字。BLS 签名算法则不同，它略微修改了哈希算法，结果对应到椭圆曲线上（的一个点）。最简单的修改是：哈希函数保持不变，将得到的哈希值作为点的 x 值寻找椭圆曲线上的对应点。通常来说（比如比特币所用的曲线），椭圆曲线有 2²⁵⁶ 个点，而 SHA-256 哈希算法的值也恰好是 256 位。不过，一个有效的 x 坐标，会对应一正一负两个 y 坐标（因为（x, y）和（x, -y）都是曲线 y²=x³+ax+b 上的点）。换句话说，新的哈希算法大约有 50% 的概率在曲线上找到 2 个对应点，另 50% 的概率则一个点也找不到（校对注：因为椭圆曲线只有 2^256 个点，如果要让每个哈希值都能找到对应点，椭圆曲线得有 2^257 个点才行）。

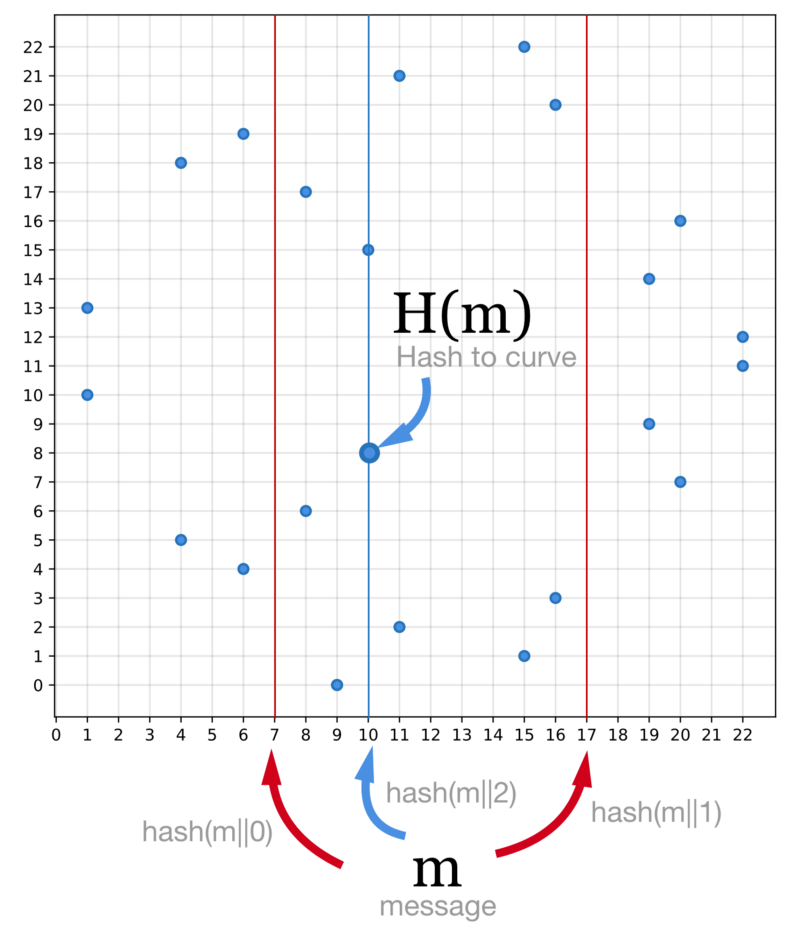
以在模为23的有限域上定义的椭圆曲线 y²=x³+7 为例。只有一半的 x 坐标在曲线上能找到对应点。此例中，我们尝试三次才成功找到对应点。

对消息求哈希时，为确保能在曲线上找到对应的点，可以在消息体后附加一个数，若（寻找对应点）失败则累加该数并重新计算。即如果 hash(m||0) 没有找到对应点，则持续尝试 hash(m||1), hash(m||2) 等，直到找到为止。当找到对应点后，在 2 个点中选择 y 坐标较小的那个作为结果即可。

曲线配对

我们还需要一个特殊的函数，能够把一条（或2条不同的）曲线上的两个点 P 和 Q 映射为一个数：

e(P, Q) → n

此函数还要有一个重要的特性。即对于未知数 x 和两个点 P 、 Q ，无论哪个点乘以 x，结果相同，即

e(x*P, Q) = e(P, x*Q)

如此，除了乘数交换仍能保持等式成立外，更进一步，以下所有的交换都要保持等式成立：

e(a*P, b*Q) = e(P, ab*Q) 
            = e(ab*P, Q) 
            = e(P, Q)^(ab)

我不准备解释这个函数是如何工作的。背后的数学原理相当复杂，如果你想知道所有 “令人厌烦” 的细节，我建议你参考这篇文章。如果你还想深入，可以研读这篇论文，它通篇讲述配对（pairings）理论。当前，我们只要假设这种函数存在，并且不会暴露 x 的任何相关信息。

值得注意的是，配对函数中不能使用任何椭圆曲线（特别是比特币的 secp256k1 椭圆曲线）。我们必须使用非常特殊的曲线（通常出自易于配对的曲线簇），才能保证函数的效率和安全。

BLS 签名方案

现在，所有构建 BLS 签名算法的基础知识已经齐备。我们用 pk 代表私钥，P = pk*G 代表公钥，m 代表要签名的消息。

为了计算签名，先对消息求曲线哈希 H(m) ，再将获取的结果（曲线坐标点）乘以私钥即可：S = pk*H(m)。大功告成！不需要随机数，不需要额外的步骤，仅仅将哈希结果乘以私钥即可。签名结果是一个曲线上的点，用压缩的序列化格式保存，只占 33 个字节。

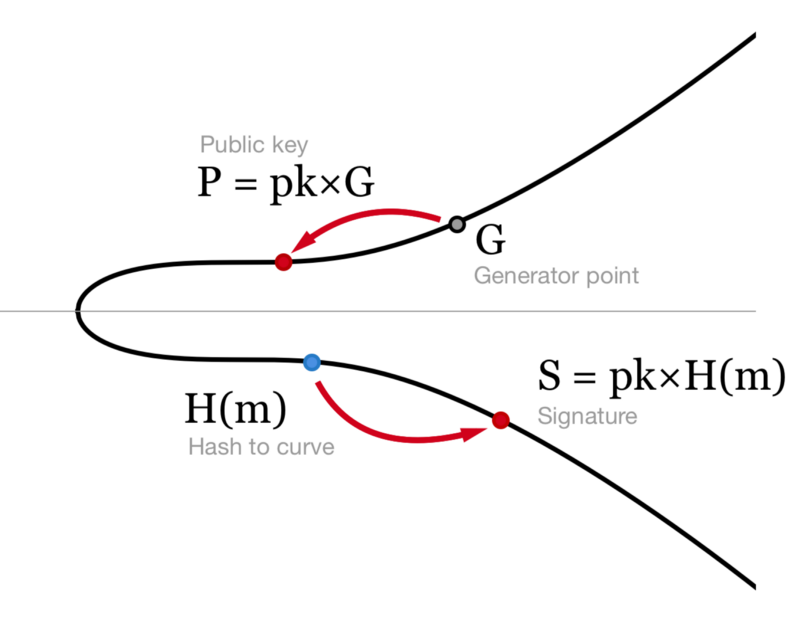
-生成 BLS 签名。将消息的哈希结果乘以私钥即可-

我们可以使用公钥 P 来验证签名，即 e(P, H(m)) = e(G, S) 。这是为什么呢？

如前所述，配对函数的特性使得如下等式成立：

e(P, H(m))  = e(pk*G, H(m)) 
            = e(G, pk*H(m)) 
            = e(G, S)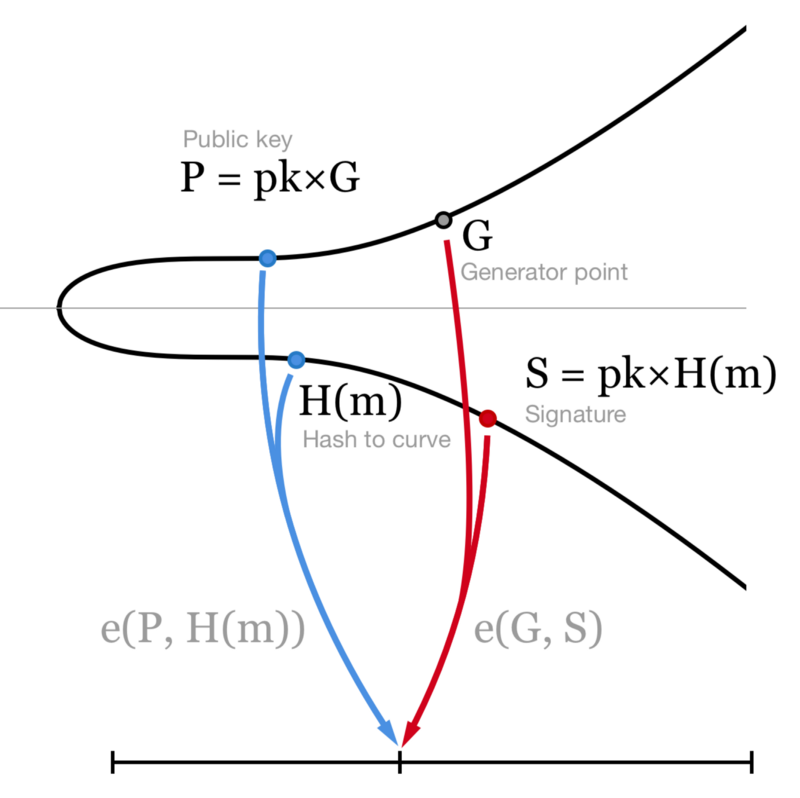

- BLS 签名验证。我们只需验证 公钥和消息的哈希值（曲线上两个点） 与 曲线生成点和签名（曲线上另两个点） 是否映射到同一个数（若是则说明这是一个有效的 BLS 签名）-

这个签名方案优美简单。对于比特币来说，该方案还有以下更棒的特性。

签名聚合

现在让我们把区块中的签名都聚合在一起。假设一个区块中有 1000 笔交易，每笔交易都由 Si（签名），Pi （公钥）和 mi（消息）组成（i 在这里表示序号）。如果这些签名可以被合并，那又何必分开保存呢？毕竟，我们只关心区块中所有的签名（而不是每一个）是否正确。为获得聚合签名，只需要将区块中的所有签名加起来：

S = S1 + S2 +…+ S1000

为验证该区块是否正确，我们需要保证以下等式成立：

为验证该区块是否正确，我们需要保证以下等式成立：

e(G, S) = e(P1, H(m1)) * e(P2, H(m2)) *…* e(P1000, H(m1000))

如果签名都有效，那么该等式的确是成立的：

e(G, S) = e(G, S1+S2+…+S1000) 
        = e(G, S1) × e(G, S2) *…* e(G, S1000) 
        = e(G, pk1×H(m1)) *…* e(G, pk1000×H(m1000)) 
        = e(pk1×G, H(m1)) *…* e(pk1000×G, H(m1000)) 
        = e(P1, H(m1)) × e(P2, H(m2)) *…* e(P1000, H(m1000))

这里我们仍需用到所有的公钥，并计算 1001 次配对函数，好处是，区块中的签名只占 33 字节了。签名聚合可以由矿工在挖矿时完成，节省大量的区块空间。

密钥聚合和 n-n 多重签名

使用多重签名的地址时，我们会对同一笔交易用不同的密钥进行签名。这种情况下，可以和 Schnorr 算法一样使用聚合密钥，把所有密钥和签名聚合成单个公钥和签名。下面我们以 3-3 多重签名方案为例（同理可推导任意数量的多重签名方案）。

一种简单的聚合方法，是把所有的签名和密钥加起来即可。如此，签名聚合结果为 S=S1+S2+S3，密钥聚合结果为 P=P1+P2+P3。可以验证以下等式依然成立：

e(G, S) = e(P, H(m))

因为：

e(G, S) = e(G, S1+S2+S3) 
        = e(G, (pk1+pk2+pk3)×H(m)) 
        = e((pk1+pk2+pk3)×G, H(m)) 
        = e(P1+P2+P3, H(m)) = e(P, H(m))

和 Schnorr 一样，我们也需要杜绝伪造密钥攻击。一种方法是要求每个签名参与者证明它拥有公钥对应的私钥（用私钥给公钥签名）。另一种方法是加入非线性系数，使得攻击无法实施。要做到这一点，聚合不再是简单的将多个密钥和签名相加，而是将它们分别乘以某个系数后再相加：

S = a1×S1+a2×S2+a3×S3

P = a1×P1+a2×P2+a3×P3

公式中签名和密钥的系数，可以通过签名者以及其它所有人的公钥计算得出，公式如下：

ai = hash(Pi, {P1,P2,P3})

举个例子，可以简单的将签名者的公钥和所有人公钥拼接在一起算出系数：

ai = hash(Pi||P1||P2||P3)

此时，上面的验证公式依然成立。虽然多了系数 ai，但计算逻辑未变。

该方案的好处是，无需在设备间进行多轮通信，只需知晓其它签名者的相应信息即可。它可比 Schnorr 算法（需要 3 轮通信）的多重签名方案简单多了。这个方案也不依赖随机性，是一种具有完全确定性的签名算法。

子群多重签名方案（m-n 多重签名）

n-n 多重签名并不常见，我们更倾向使用 m-n 多重签名（比如 2-3 多重签名）。我们不想因为丢失（n 个密钥中的）一个密钥而一无所有。密钥聚合非常适合这种场景。在 Schnorr 签名算法中，我们用公钥组成的默克尔树来实现密钥聚合，这种方式效率不高，但是将将堪用。不幸地是，当 m 和 n 的值变大时，默克尔树的大小会呈指数增长。

BLS 使用了另一种方法，不过略复杂。我们需要一个普通哈希函数 hash(x) （结果为一个数）和一个曲线哈希函数 H(x) 。开始多重签名时，还需要一个初始化过程，这之后，签名者之间就不再需要通信了，只需提供交易签名即可。

举个简单的例子，我们要创建一个 2-3 多重签名，3 个签名存储在不同的设备上（这个例子可以扩展为任意的 m-n 多重签名）。

初始化（生成成员密钥）

用 i = 1,2,3 来表示集合中相应位置的设备，用 pki 表示私钥，用 Pi = pki×G 表示公钥。我们用前面说的方法来聚合公钥：

P = a1×P1+a2×P2+a3×P3, ai = hash(Pi, {P1,P2,P3})

现在，每个设备都需要对每个 i 签名，以证明该 i 是聚合公钥中的一员。将签名聚合后，保存在对应的设备中：

MKi = (a1*pk1)*H(P, i) + (a2*pk2)*H(P, i) + (a3*pk3)*H(P, i)

这个签名被称作“成员密钥”，稍后签名时我们会用到。每个成员密钥都是对消息体 H(P,i) 的 n-n 多重签名，即：

e(G, MKi)=e(P, H(P,i))

因为：

e(G,Mki) = e(G, (a1*pk1)*H(P, i) + (a2*pk2)*H(P, i) 
              + (a3*pk3)*H(P, i))
         = e(G, (a1*pk1 + a2*pk2 + a3*pk3)*H(P, i))
         = e(G*(a1*pk1 + a2*pk2 + a3*pk3), H(P, i))
         = e((G*a1*pk1 + G*a2*pk2 + G*a3*pk3), H(P, i))
         = e(P, H(P,i))

记住这个等式，稍后还会用到。它用来证明某个设备是多重签名中的合法参与者。

签名

假设只用私钥 pk1 和 pk3 给交易签名，我们会生成 2 个签名 S1 和 S3：

S1 = pk1×H(P, m) + MK1, S3 = pk3×H(P, m) + MK3

将它们加起来，聚合成单一的签名和公钥：

(S’, P’) = (S1+S3, P1+P3)

用 P’ 和 S’，是为了强调它们只是由部分签名者参与计算的（公钥和签名），而不像 P 那样是由所有签名者参与计算的（公钥）。为了验证 2-3 多重签名，需证明如下等式成立：

e(G, S’) = e(P’, H(P, m)) * e(P, H(P, 1)+H(P, 3))

上面说过，成员密钥 MK1 和 MK3 是对消息 H(P, 1) 和 H(P, 3) （消息本身由聚合公钥 P 签名）的签名，所以有：

e(G, S’) = e(G, S1+S3)
         = e(G, pk1*H(P, m)+pk3×H(P, m) + MK1 + MK3) 
         = e(G, pk1*H(P, m)+pk3×H(P, m)) * e(G, MK1+MK3)
         = e(pk1*G+pk3*G, H(P, m)) * e(P, H(P, 1) + H(P, 3))
         = e(P’, H(P, m)) * e(P, H(P, 1)+H(P, 3))

证明完毕。比 n-n 多重签名复杂一些，但仍然可以理解。

在比特币中的实现

要在比特币上部署一个 BLS 多签名钱包时，我们需要往某个地址（该地址由聚合公钥 P 生成）打钱。假设我们希望这是一个 2-n 多签名合约，那么可以用比特币的锁定脚本来描述，声明如下：

OP_2 <P> OP_CHECK_BLS_MULTISIG

OP_2 表示需要2个密钥进行签名。这里没有指明总共有 3 个签名，因此它可以表示 2-3 或者 2-100 等不同的多重签名地址。如此，总签名数永远不会暴露。

为了花掉输出（output）地址中的钱，则需要提供 P’ （公钥），S’（签名 ）以及参与签名者的编号（这个例子中是 1 和 3）。解锁脚本如下：

OP_1 OP_3 <P’> <S’>

脚本中有了这些信息，就足够用来验证交易了。其中，OP_1 和 OP_3 告诉我们需要计算的曲线哈希为 H(P, 1) 和 H(P, 3)。

如此，对于任意 m 和 n 的多重签名，我们只需要以下信息：

• 一个用在加锁脚本中的聚合公钥 P
• 一个由部分参与者（m 个）生成的聚合公钥 P’ （用在解锁中）
• 一个聚合签名 S’
• 解锁要求的参与者数量 m

一切简单而优美！

由于比特币地址通常只用一次，需要使用 BIP32 这种密钥推导算法生成新的私钥和地址。因此，每次生成新的私钥时，我们也需要生成对应的成员私钥，我不太喜欢这一点。为避免每次交易后都要初始化生成成员私钥，可以一次性地生成一批（比如 1000 个）成员私钥，毕竟每个私钥只占 32 字节。如此，当 1000 个地址用完后，我们才需要再次进行初始化。

缺点

鉴于大家在评论和 twitter 的提醒，我认识到有些地方我考虑欠周，会让你们误以为 BLS 签名算法是完美的。它并不完美。谢谢你们的提醒！

我完全忽略了配对计算的高复杂度。我们曾认为配对函数 e(P, Q) 既高效又安全，实际上它并不完全是。

配对函数并不那么高效

BLS 签名验证的复杂度要比 ECDSA 高上一个数量级。在验证区块中 1000 笔交易的聚合签名时，仍需要进行 1000 次配对计算，这可能比使用 ECDSA 时（对 1000 个单独签名进行验证）还要慢。唯一的好处在于，可以在区块中放更多笔的交易，毕竟聚合签名只占 32 字节。

与 BLS 不同，Schnorr 验证算法的效率很高，它可以把签名放一起验证，效率是 ECDSA 算法的三倍。这样，问题来了，效率和安全哪个对我们更重要？

想要安全，更难！

配对函数十分复杂，使用不当就会反受其累。一方面，我们希望用高效的配对函数来加快签名验证，另一方面，我们又希望密钥信息暴露越少越好。两者互相矛盾，我们需要异常小心地选择适宜配对的曲线。

有一种针对椭圆曲线加密体系的攻击，叫 MOV 攻击（用攻击发现者 Menezes、Okamoto 和 Vanstone 的名字命名），它能利用配对函数来危害系统安全。所以，使用配对函数必须万分小心。

总结

BLS 签名算法很出色——它能将区块中的签名聚合成单一签名；能进行密钥聚合和 m-n 多重签名（无需额外通信）；能避免使用随机数生成器。这些优点使它显得如此简单优雅。当然，它仍有改进空间，标准化和优化也尚需时日。但我希望有朝一日，它能变得足够好，可以被纳入比特币协议中。这样的话，我们不但能获得它出色的功能，还可享受体积更小、聚合度更强的签名算法带来的好处。

BLS 算法的第一作者 Dan Boneh，目前正投身于对加密货币的研究，这使我异常兴奋。他是一位杰出的密码学家，他所执教的密码学课程也很棒。在这里，我还要推荐下他尚未完成的密码学著作。相信不久的将来，他和他的团队会带来更多针对加密货币的有趣方案和协议改进。

原文链接: https://medium.com/cryptoadvance/bls-signatures-better-than-schnorr-5a7fe30ea716 作者: Stepan 翻译&校对: wuwei & 阿剑

本文由作者授权 EthFans 翻译及再出版。