LossyDAS:数据可用性的有损、增量和对角抽样 - 分片
- 以太坊中文
- 发布于 2024-03-13 12:15
- 阅读 1061
本文探讨了数据可用性抽样(DAS)中的若干关键问题,并提出了三项改进技术:LossyDAS允许在抽样中存在少量缺失,以换取更大的抽样规模;IncrementalDAS逐步增加抽样规模,若测试失败则扩展样本;DiDAS则通过选择行和列不同的样本,优化了二维Reed-Solomon编码网格的抽样效果。这些方法旨在提高DAS的效率和可靠性,尤其是在面对恶意攻击时。
作者: @cskiraly, @leobago, 和 @dryajov,来自 Codex 团队。
本文旨在与社区分享我们关于 DAS 的一些发现。这些内容去年已经与你们中的一些人分享过,作为参考,我们链接了 原始文档。在下面,我们希望提供一个更容易理解的摘要。
TL;DR
- DAS 的一个重要参数是样本大小,即节点下载和验证的段(或列)的数量。允许一些缺失的段,并拥有稍微大一点的样本大小,有时比拥有较小的样本大小但试图不惜一切代价检索样本的所有段更好。我们将这种技术称为 LossyDAS。
- 可以逐渐增加样本大小,如果在测试失败(或未在给定的时间内得出结论)时扩展样本。我们将此策略称为 IncrementalDAS。
- 在选择在 2D Reed-Solomon 编码网格上采样什么时,通常的假设是使用均匀随机选择。我们表明,选择行和列不同的样本,我们称之为 DiDAS(“不同”或“对角线” DAS),提供了概率上更好的结果。它实现起来很简单,而且似乎没有任何缺点。
Intro
分片和 DAS 已经在进行中一段时间了。虽然 最初的论文 和 Danksharding 提案 侧重于 2D Reed-Solomon (RS) 编码,但一些 最近的帖子 提出了过渡性的一维编码。在这篇文章中,我们重点关注抽样及其概率保证的一些方面,并提出了对系统的三个改进。下面描述的技术是为原始 2D RS 编码的情况开发的,但在某种程度上也适用于过渡性提案。
首先,我们介绍用于数据可用性的有损抽样(LossyDAS),它提供了与随机均匀抽样相同的概率保证,增加了误差容限以换取稍微更大的样本大小。
其次,我们讨论 IncrementalDAS,它为开发具有增加样本大小的动态抽样策略提供了基础。
最后,我们介绍用于数据可用性的对角线抽样(DiDAS),该方法改进了对这种特定 2D 纠删码的抽样性能,为最坏情况下的“对抗性”擦除模式提供了比均匀随机抽样更好的性能。
Sampling over the DAS encoding
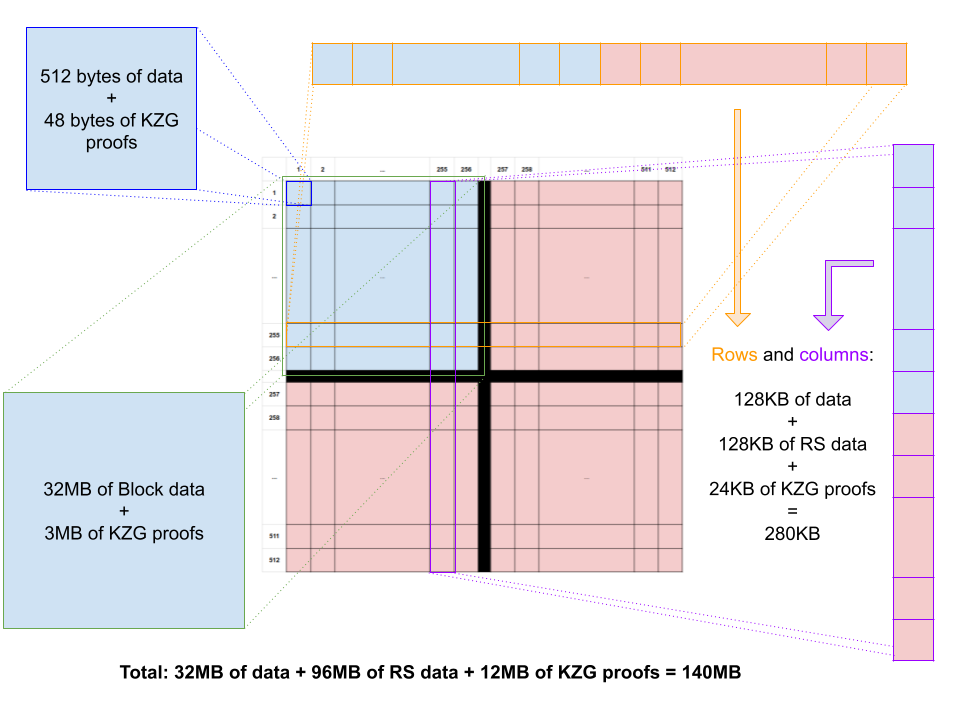
图 1:数据可用性编码结构
图 1 显示了 Danksharding 中提出的 2D 数据可用性编码,使用正方形结构,在两个维度上使用相同的 K=256 和 N=512 的 RS 代码。这意味着如果至少有 K=256 个段可用,则可以完全恢复任何行或列。
在基线抽样过程中,一个抽样节点均匀随机地选择 S 个段,不放回,并尝试从网络下载这些段。如果可以检索所有 S 个段,则它假定该块可用。如果其中至少有一个失败,则它假定该块不可用。
Sample Size and Erasure Patterns
DAS 的一个重要参数是样本大小 S,即节点下载和验证的段的数量。在评估需要多少样本时,重要的是要注意,与简单的 RS 代码相反,多维代码是非 MDS(最大距离可分)的。使用 MDS 代码,可修复性仅取决于丢失的段的数量,但使用非 MDS 代码,它还取决于实际的擦除模式。这意味着,在某些概率下,会发生非平凡的擦除模式。更重要的是,这可能允许恶意行为者在系统中注入精心设计的(对抗性)擦除模式。因此,在分析抽样作为测试时,我们应该区分以下情况:
- 随机擦除,
- 对抗性(例如,最坏情况)擦除模式。
Random Erasures
当考虑网络和存储引起的错误时,随机擦除是一个合理的模型。随机擦除的最简单模型是均匀随机擦除的情况,当假设诚实的行为者时,它相对较好地映射到 DHT 提供的服务,如原始提案中所述。但是,鉴于系统的性质,我们的主要优化目标不是这个,而是最坏情况或对抗性擦除。
Worst-case Erasures
当考虑恶意行为者时,分析最坏情况的场景非常重要。虽然该代码不是 MDS 代码,但我们可以描述什么是最坏情况(或最小大小)的擦除模式。如果我们选择任何 N-K+1 行和 N-K+1 列,并删除这些选定行和列的交集中的所有段(即 512 512 个段中的 257 257 个段),我们阻止任何恢复发生。只有完整的行和不可恢复的行,类似地,只有完整的和不可恢复的列。因此,无法恢复任何行或列,数据丢失。
很容易看出以上是“最坏情况”。首先,观察到这里最坏情况意味着最少数量的缺失段。在我们的上下文中,这也意味着恶意行为者应控制的最少数量的节点/验证器才能实施攻击。在最坏情况下,不应有可能修复行或列。假设存在一种最坏情况的模式,其缺失段的数量少于 (N-K+1) * (N-K+1)。在这种情况下,至少会有一列或一行具有少于 N-K+1 个缺失段。该列/行是可修复的,这与我们的假设相矛盾。
注意:以上证明假设了一个交互式的基于行/列的修复过程。也可以使用多元插值来修复多维 RS 代码,如 此处 讨论的那样。他们论文中描述的证明也适用于我们的情况,确认这些模式是最坏情况的最小大小模式。
显然,任何包含最坏情况擦除模式的擦除模式也是不可恢复的。
Setting the Sample Size
在设置样本大小时,我们感兴趣的是限制不可用块通过测试的概率,换句话说,独立于擦除模式的假阳性 (FP) 率。显然,使用均匀随机抽样,假设擦除模式使块不可恢复,则模式越大,越容易检测到它。因此,研究最小的此类模式,即最坏情况的擦除模式就足够了。此概率可以近似为二项分布,或者 - 更好的是 - 使用具有以下项的超几何分布精确计算:
- 总体大小:N*N
- 总体中的失败状态数:(K+1)*(K+1)
- 段数:S
- 允许的失败数:0
Pr(X=0) = Hypergeom(0; N^2, (N-K+1)^2, S)
此概率显然取决于样本大小 S。事实上,我们的实际问题是:
我们需要多少段才能达到给定的保证级别?
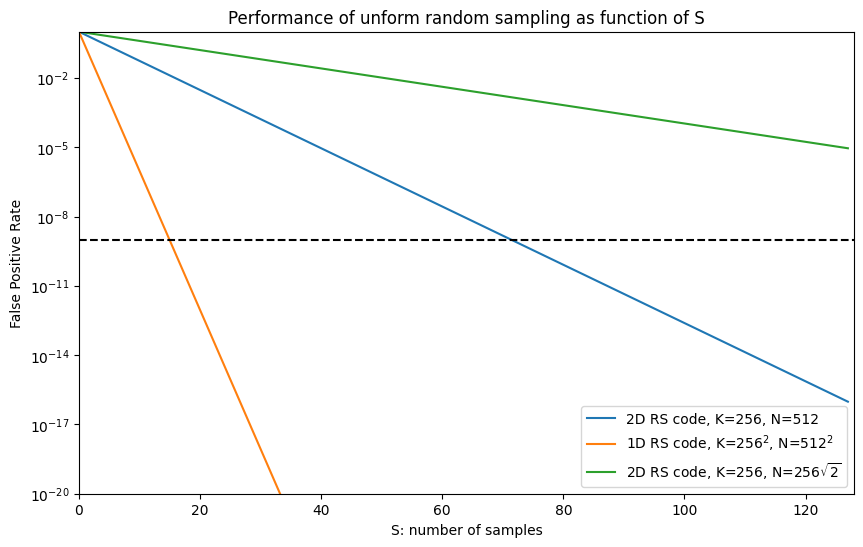
如图 2 所示,如果我们有 2D RS 编码,K=256,N=512,并希望此概率低于 1e-9,则我们需要 S=73 个段。该图还显示了使用具有相同段数和相同扩展因子的 1D RS 代码的理论情况,以及具有较小扩展因子的 2D RS 代码的情况。
 \
das-uniform-sampling863×547 37.8 KB
\
das-uniform-sampling863×547 37.8 KB
图 2:在 DAS 数据结构上进行均匀随机抽样的性能,具有不同的 RS 编码,作为样本大小 S 的函数
What about False Negatives?
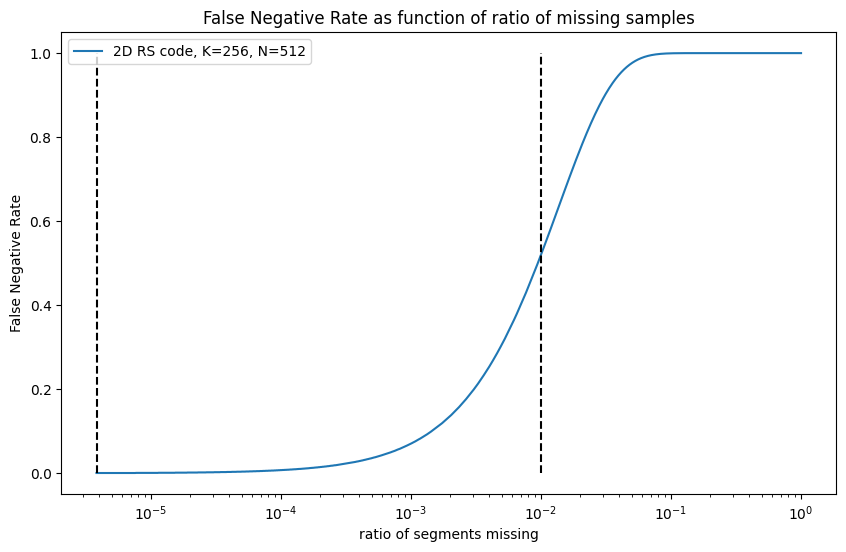
与所有统计测试一样,既有 FP(假阳性:即使块不可用,测试也通过)的情况,也有 FN(假阴性:即使块可用,抽样也失败)的情况。可以使用超几何分布的生存函数来量化假阴性测试的比率,如下所示:
P_{FP} = Pr(\{X>0\}) = Hypergeom.sf(0; N^2, M, S)
其中 M 是擦除模式的大小。
 \
das-false-negative846×552 26.3 KB
\
das-false-negative846×552 26.3 KB
图 3:作为缺失样本函数的假阴性率
例如,如果 512*512 个段中仅缺少 1 个段,则 FN 测试结果的概率为 0.03%。如果缺少 1% 的段(2621 个段),则 FN 测试的概率为 51.9%。
那么,当由于少量段的不可用而导致大量 FN 测试时,此系统如何工作?更具体地说,这里至少有两个导致 FN 情况的问题:
- 在具有大量节点的分布式设置中,总是存在瞬时错误,例如节点关闭、无法访问或遭受网络错误。要求接收所有段意味着我们应该使用可靠的传输机制(例如,TCP 连接,或在失败的情况下进行重传的其他方式),即使这样,我们也需要节点具有相对较高的可用性和良好的网络连接。或者,我们需要协议以冗余方式存储数据并使用多个并行查找来检索数据,就像典型的 DHT 一样,我们仍然可能需要大的冗余和许多检索。
- 正如我们所看到的,要求接收所有段也意味着如果并非所有段实际上都可用,我们的测试中可能会有大量的假阴性。换句话说,当数据在分布式结构中存在一些损失时,测试很容易失败,但它实际上可以作为一个整体重建。虽然我们可以通过复制、重试和修复来避免一些损失,但如果由于前一点而不可能,这可能会非常昂贵。
要了解可以做什么,让我们仔细分析我们到目前为止的基本前提,重点关注几个关键部分:
“当一个节点无法检索 所有 S 个选定的段时,它无法接受该块。”
- “无法检索”:在这种上下文中,“无法检索”实际意味着什么,需要更多关注。这意味着我们尝试、重试,但无法检索。节点应该尝试检索一个段多长时间以及使用什么动态?它是否还应尝试通过使用纠删码进行重建来检索它?我们认为这些网络级别的可靠性技术可能很昂贵,并且在使网络更可靠和选择正确的抽样过程之间存在权衡。
- “所有”:我们真的需要检索所有段吗?要求更多段并允许一些损失不是更有意义吗?
- “S”:如果我们的第一次尝试失败,我们可以动态更改 S,寻找更多样本吗?
要回答“无法检索”意味着什么,我们应该深入研究网络协议的细节。我们将其留给后续帖子。在下面的内容中,我们讨论了其他两种可能性。LossyDAS 解决了是否需要“所有”样本的问题,而 IncrementalDAS 则侧重于使“S”动态化。DiDAS,相反,侧重于以更小的“S”实现相同的概率保证,
LossyDAS:接受部分抽样
我们真的需要样本的所有段吗?如果我们测试更多段,并允许一些损失,会发生什么?事实证明,我们可以使用这些假设来定义测试。
在 LossyDAS 中,就像在原始测试中一样,我们设置目标 FP 概率(即,测试通过的情况,我们认为数据已经发布,但实际上它处于不可修复的状态)。我们寻找 S(样本大小)的最小值,作为以下因素的函数:
- P_{FP}:目标 FP 概率阈值,以及
- M:我们允许在查询的 S 个段中丢失的段数
在计算中,我们使用百分点函数 (PPF),它是 CDF 的逆函数。
图 4:在 LossyDAS 中可以允许的失败次数,同时遵守给定的 FP 阈值
正如我们在图 4 中看到的那样,我们可以稍微多抽样并允许损失,同时保持相同的 FP 阈值。例如,对于 1e-9 的目标 FP,我们可以选择 84 的样本大小并允许 1 个缺失段。或者我们可以选择 103 个段并最多允许 3 个损失。一般来说,代替以 n=73 进行的抽样,大约每增加 10 个段,我们就可以容忍一个额外的缺失段。
实际上,这意味着节点可以尝试下载稍微多一点的段,这已经考虑了潜在的网络问题或其他瞬时错误。
IncrementalDAS:动态增加样本大小
当实际丢失的段太多时会发生什么?我们应该等待这些段被修复、自己修复它们,还是我们可以做其他事情?有人可能会试图争辩说,应该使测试失败,直到修复所有测试的段,否则该块不可用,但是我们整个概率保证系统是建立在确保可修复性(而不是修复)的原则之上的。此外,等待它被修复可能太长,而自己修复可能太昂贵。自然而然地出现的问题是,我们是否可以以某种方式使用不同的样本重新测试。
首先,我们应该澄清,简单地在另一个具有相同 S 的随机样本上进行另一个测试是一个坏主意。那将是“掷Coin直到你喜欢结果”的方法,这显然是错误的。它打破了我们先前设置的 FP 阈值的假设。如果我们进行另一个测试,则应基于我们已经知道的条件概率。这就是 IncrementalDAS 的目标。
在 IncrementalDAS 中,我们的节点根据 LossyDAS 选择第一个目标损失大小 L1,以及相应的样本大小 S(L1)。它请求这些段,允许 L1 损失。如果它收到至少 S(L1) - L1 个段,则测试通过。否则,它使用一些 L2>L1 将样本扩展到大小 S(L2)。通过扩展样本,我们的意思是它选择新样本,使其包含旧样本,它只是选择 S(L2)-S(L1) 个新的随机段。很容易看出我们可以做到这一点,因为我们可以从一开始就使用更大的样本,并且从概率保证的角度来看,这会很好。我们分两步进行抽样的事实并没有改变这一点。显然,该过程可以继续进行,越来越大地扩展样本。L2(以及进一步的扩展)可以根据先前步骤中观察到的实际损失数量来确定。可以使用不同的策略,也可以基于使用的所有其他恢复机制,我们在此处不做详细说明。
DiDAS:避开均匀随机抽样
到目前为止,我们的假设是使用均匀随机抽样来处理纠删码块结构。但是,该代码不是 MDS,因此某些段组合似乎比其他组合更重要。
在测试的基本版本中,我们均匀随机地选择段,而不替换整个正方形。其中一些段可能落在同一行或同一列上,这降低了测试的效率。相反,如果不是基本版本,我们确保使用在不同行和不同列上的段进行测试,那么我们会增加捕获这些最坏情况擦除的可能性。我们将此抽样称为用于数据可用性的不同(或对角线)抽样 (DiDAS)。
注意:我们在此处定义的是无替换抽样的 2D 变体。对角线显然是行和列不同的段选择,但当然还有许多其他可能的选择。从理论的角度来看,在最坏情况的擦除模式下,整个纠删码结构对于行和列排列是不变的。因此,在研究参数时,我们可以假设对角线中的样本和擦除模式的排列。
How much we improve with DiDAS
使用新的抽样方法,从 S 个段中捕获最坏情况擦除的可能性可以表示为两个超几何分布的组合。有关确切的公式,请参见我们的 原始工作文档(Jupyter Notebook)。图 5 显示了在最坏情况擦除模式下两种抽样方法之间的差异。
图 5:均匀随机抽样与 DiDAS 的比较,其中 N=256、K=512 和最坏情况的擦除模式
直观上,对于小 S,差异可以忽略不计:即使我们不强制不同的行和列,抽样的段也最有可能位于不同的行和列上。从这个意义上讲,S=73 仍然相对较小。
对于较大的 S,如图 5 所示,在对数尺度上差异变得显着。但是,我们说的是非常小的概率,并且我们承认,对于当前提出的参数集,这在实践中有多大用处是值得怀疑的。
但是,实现 DiDAS 是很简单的。如果我们将它与 IncrementalDAS 结合使用,则可以帮助减少所需的增量大小。
另请注意,DiDAS 不能超过 S=N,因为没有更多不同的行或列。当 S=512 时,DiDAS 总是发现不可恢复的最坏情况擦除模式,概率为 1。这可能吗?实际上,确实如此,但仅对于先前定义的最坏情况模式,对于 DiDAS 而言,这不是最坏情况。有些擦除模式比最小大小的擦除模式对 DiDAS 更糟。但是,我们的初步结果表明,这些必然是容易检测到的大模式,并且 DiDAS 在这些模式上的性能仍然优于均匀随机抽样。
Acknowledgements
This work is supported by grant FY22-0820 on Data Availability Sampling from the Ethereum Foundation. We would like to thank the EF for its support, and Dankrad Feist and Danny Ryan for the original proposal and the numerous discussions on the topics of the post.
References
[1] Original working document (Jupyter Notebook).
[2] Al-Bassam, Mustafa, Alberto Sonnino, and Vitalik Buterin. “Fraud and data availability proofs: Maximising light client security and scaling blockchains with dishonest majorities.” arXiv preprint arXiv:1809.09044 (2018).
[3] Dankrad Feist. “New sharding design with tight beacon and shard block integration.” blog post, available at
[4] Valeria Nikolaenko, and Dan Boneh. “Data availability sampling and danksharding: An overview and a proposal for improvements.” blog post, available at
[5] From 4844 to Danksharding: a path to scaling Ethereum DA
- Full DAS Sampling Analysis
- Improving DAS performance with GossipSub Batch Publishing
- FullDAS: towards massive scalability with 32MB blocks and beyond
- Accelerating blob scaling with FullDASv2 (with getBlobs, mempool encoding, and possibly RLC)
- 原文链接: ethresear.ch/t/lossydas-...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 0
- 分类: 以太坊
- 标签: 数据可用性抽样 DAS 分片 Reed-Solomon编码 LossyDAS IncrementalDAS DiDAS
- Zero 链: 技术定位报告 215 浏览
- 区块链 101:数据处理 1424 浏览
- 以太坊 Fusaka 升级带来了哪些改进 3612 浏览
- Fusaka更新 - 面向Blob用户的信息 1151 浏览
- 宁静阶段 0 37 浏览
- 精简以太坊 1412 浏览
- Blob公证人:用于扩展DA的分片分布式Blob发布设计 1212 浏览
- 区块链Layer 1与Layer 2可扩展性解决方案 868 浏览
- 2025年将PeerDAS推向主网之路 979 浏览
- Additive FFT:背景 1672 浏览
- DAS和分片Blob Mempool的新设计 - 分片 1329 浏览
- DAS和分片Blob内存池的新设计——分片 1344 浏览

 \
das-structure960×720 62 KB
\
das-structure960×720 62 KB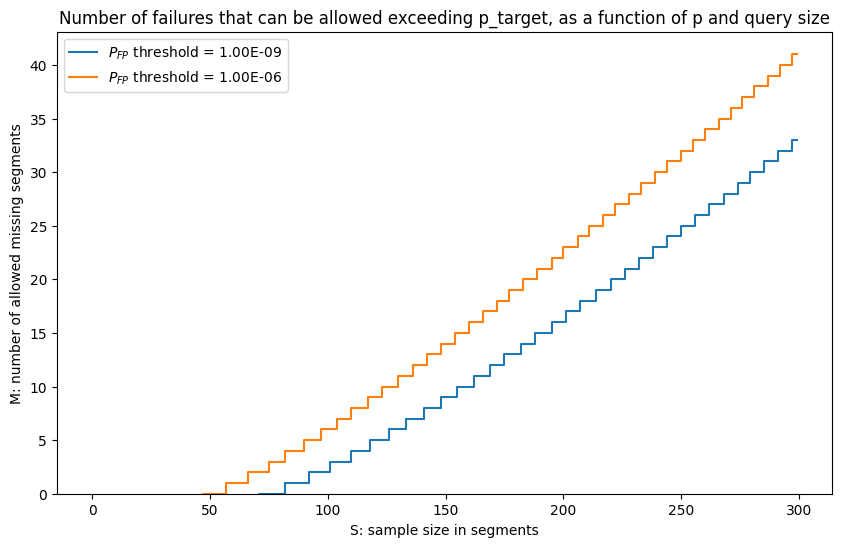 \
das-lossydas841×547 24.9 KB
\
das-lossydas841×547 24.9 KB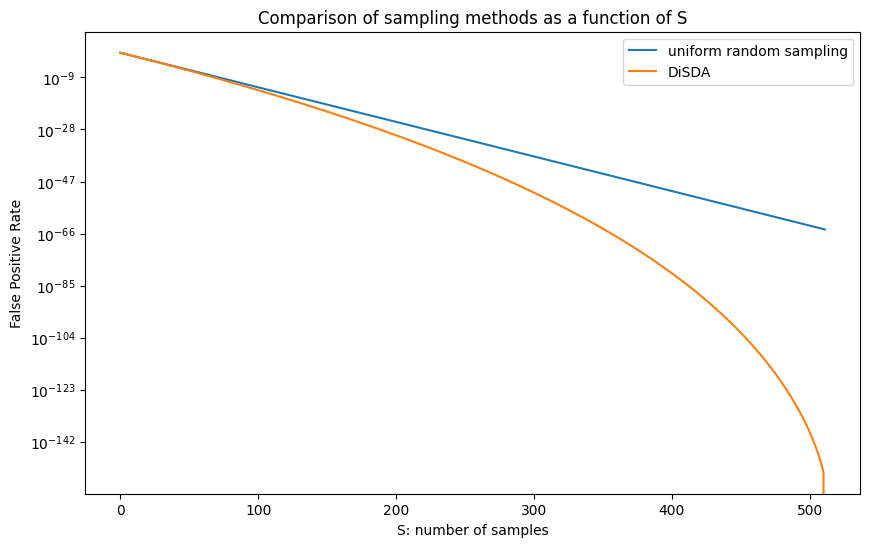 \
das-didas870×547 30.1 KB
\
das-didas870×547 30.1 KB
