大规模共识的签名合并 - 密码学
- 以太坊中文
- 发布于 2023-11-11 21:36
- 阅读 1036
本文深入探讨了在大规模共识系统中使用的签名聚合技术,特别关注了以太坊的Proof-of-Stake(PoS)区块链如何通过签名合并(Signature Merge)方案来解决bitfield合并问题。
大规模共识的签名合并
作者:George Kadianakis, Dmitry Khovratovich, Zhenfei Zhang, Mary Maller
\cdot
特别感谢 Jeremy Bruestle, Vitalik Buterin, Srinath Setty 和 Arantxa Zapico!
\cdot
在这篇文章中,我们专注于为权益证明区块链执行大规模签名聚合的工具。
我们首先在以太坊共识协议的背景下提出位域合并问题。为了解决这个问题,我们引入了一种名为签名合并的新签名聚合技术,并演示了如何在以太坊中使用它。然后,我们通过递归 SNARK 和去中心化证明,使用携带证明数据 (PCD) 技术提供了三种签名合并的实例化。除了这些方法之外,我们还强调了与 PCD 构造的可扩展性相关的开放研究挑战。最后,我们提供初步的性能评估,让读者了解这些方案的预期效率。
简介
权益证明 (PoS) 系统本质上是开放的投票系统,验证者需要达成共识。在这些共识系统中,加密签名充当选票。验证者通过签署同一消息公开表明他们的同意。
我们希望未来的 PoS 系统能够以大规模运行,可能需要数百万选民,正如以太坊的 单Slot最终性 方案所要求的那样。在如此庞大的 P2P 系统中,优化这些签名的收集方式至关重要。
签名聚合
签名聚合方案允许多个签名合并为一个。即使有大量的验证者,聚合也能显著减少系统的通信和验证开销。一个著名的此类方案是 BLS 签名方案。
使用 BLS,可以轻松聚合签名,但跟踪签名者的身份需要另一层表示——这就是以太坊使用位域的地方。这些位域充当一种“参与者列表”,标记验证者中哪些人已签署消息。位域是参与者列表的二进制表示:索引 i 处的 “1” 表示索引 i 处的验证者已签署消息。
了解参与者的身份对于以太坊共识至关重要,因为 罚没、质押奖励 和 非活动泄漏。
位域合并问题
考虑一个签名聚合系统,其中一个 收集器 实体需要聚合两个聚合签名及其位域。聚合签名很容易,但合并位域可能很棘手。
例如,考虑两个位域:110 和 010。合并它们并不像求和数字那么简单。后者将导致 120,这是一个非二进制值,并且在网络上发送的成本要高两倍。
此外,BLS 验证者必须知道在验证期间签名已被聚合了多少次,以便她可以计算正确的验证密钥。也就是说,120 背后的聚合签名与 110 背后的签名具有不同的验证密钥。
共识中的位域合并问题
当在树的上部聚合已经聚合的签名时,在 基于树的聚合拓扑 中会遇到上述问题,如 Horn 提案 中所讨论的那样。
这个问题也可以在 基于 Gossip 的聚合拓扑 中看到,其中聚合以混乱的非确定性方式传播,如下图所示,Vitalik 过去曾建议过。对于具有大量验证者但联网节点数量较少的网络,基于 Gossip 的聚合可能比基于树的结构更有效:在这种情况下,如果 Alice 有 1000 个验证者,她可以用权重为 1000 的已填充位域启动协议,而无需任何事先的通信。此外,基于 Gossip 方法的非结构化属性可以允许更友好的隐私聚合协议。
由于带宽是 P2P 系统的基本扩展因素,我们希望继续使用位域来表示参与,因为使用更重的表示会给网络层带来更大的压力。
我们将累积两个位域并生成位域的操作称为 合并。
在这篇文章中,我们提出了 签名合并 方案来解决位域聚合问题,以及使用 SNARK 的三种可能的实例化。
签名合并方案
签名合并 (SM) 方案 支持递归合并签名及其位域,同时仍然允许从中提取签名者集。在本节中,我们介绍 SM 方案的接口,并在 附录 A 中展示了如何在以太坊的上下文中使用它。
按照 [GV22] 的步骤,SM 方案在功能上与经典的签名聚合方案相似,但它们引入了 Merge、MergeVerify 和 GetSigners 算法。
此外,MergeVerify 函数不接受特定的验证密钥作为输入。相反,它具有对 PKI 系统的 Oracle 访问权限,可以使用用户的索引或参与位域查询以检索验证密钥。每次调用 Keygen 时,都会更新 PKI 系统。
最后,GetSigners 方法返回一个位域,其中包含所有参与签名者的索引。
一个 签名合并 (SM) 方案 具有以下算法:
-
Setup(1^\lambda) \rightarrow pp: 输出公共参数 pp,这些参数隐式地提供给所有算法
-
Keygen(1^\lambda, \text{PKI}) \rightarrow (\text{sk}, \text{vk}, k): 为用户生成秘密签名密钥和公共验证密钥,并将公钥注册到 \text{PKI}。还在 \text{PKI} 系统中返回用户的索引 k。
-
Sign(\text{sk}, m) \rightarrow \sigma: 接收签名密钥 sk 和消息 m 作为输入,并计算签名 \sigma
-
Verify(\text{vk}, \sigma, m) \rightarrow 0/1: 接收验证密钥 \text{vk}、消息 m 和签名 \sigma 作为输入,并返回签名是否有效。
-
Aggregate ^\text{PKI}(m, \{ ( \sigma_i, k_i ) \}_i) \rightarrow \pi : 聚合算法接收一系列带有用户 PKI 索引 k_i 的签名 \sigma_i 作为输入,并输出一个合并的签名 \pi。它还可以访问 PKI 系统,该系统可以查询以检索任何验证密钥。
-
Merge ^\text{PKI}(m,\{ \pi_i \}_i) \rightarrow \pi: 合并算法接收一系列合并的签名 \pi_i 作为输入,并输出一个合并的签名 \pi。它还可以访问 PKI 系统,该系统可以查询以检索任何验证密钥。请注意,
Merge允许我们组合合并的签名 \pi_i,而无需知道任何底层单个签名 \sigma_i。 -
MergeVerify ^\text{PKI}(m, \pi) \rightarrow 0/1: 合并的签名验证算法接收消息 m 和合并的签名 \pi 作为输入,并输出签名是否有效。它还可以访问 PKI 系统,可以查询以检索任何验证密钥。
-
GetSigners ^\text{PKI}(\pi) \rightarrow b: 给定一个合并的签名 \pi,返回一个位域,对应于所有参与签名者的索引。
请注意,合并的签名的大小必须与签名者的数量成线性关系,否则 GetSigners 方法将无法恢复合并签名的所有签名者,从而违反了不可压缩性。
如果 \pi 的大小最小,我们说签名合并方案是 轻量级的:它仅为 PKI 系统的每个用户使用一个位。在这篇文章中,我们只关注 轻量级签名合并 方案。
签名合并方案的安全性
SM 方案的安全性定义类似于聚合方案。令 i 表示诚实签名者的索引。如果任何多项式时间对手都无法生成验证 (m, \pi) 使得 b = \mathbf{GetSigners}^\text{PKI}(\pi) 并且 b 的第 i 位等于 1 (b_i = 1),除非方 i 先前已签署 m,则 SM 方案是不可伪造的。
签名合并实例化
在接下来的章节中,我们将提供递归 SNARK 和 PCD 的入门知识,然后通过不同的递归 SNARK 范例,介绍三种不同的方法来实现签名合并方案。
使用递归 SNARK 的携带证明数据
递归 SNARK 是一种密码学证明系统,其中 SNARK 验证者足够简洁,可以在另一个 SNARK 电路内部进行评估。这种“嵌套”可以重复执行,从而允许将多个证明聚合为一个。
当与 携带证明数据 (PCD) 范例 结合使用时,我们可以开始将参与位域视为签名合并系统的主要对象。位域(在上图中描述为 m_i)始终与关联的证明(描述为 \pi_i)一起传输。接收者可以验证该证明,并确信该位域是一系列有效签名验证和位域合并的产物。
方法 1) 递归 STARK
在本节中,我们将介绍一个简单的 签名合并 方案 基于递归 STARK。
该方法基于递归 STARK 电路,该电路使用签名或其他 STARK 及其关联的位域。该电路验证接收到的每个签名和 STARK,并合并其位域。电路的输出是合并的位域和 STARK 证明。
虽然这不是我们建议的方法中最有效的方法,但它是概念上最简单的方法,并且还提供后量子保证。
在这里,STARK 是多项式方程的基于哈希的证明,该方程对特定的计算进行编码。递归 STARK 的特殊之处在于,该计算包含其他 STARK 的验证。因此,合并步骤包括以下内容:
- 使用其自己的位域验证传入的 STARK 证明。
- 创建一个 STARK 证明,证明传入的证明有效,并且其位域的并集等于所声称的结果。此步骤需要构建许多对整个计算跟踪进行哈希处理的 Merkle 树,即验证 STARK 并联合位域。
- 发布 STARK 证明,其中包含刚刚构建的 Merkle 树中的多个打开。
递归 STARK 电路
使用一个简单而精简的基于哈希的 签名方案(例如 Winternitz)而不是 BLS,我们引入以下递归 STARK 关系:
- 公共输入:所有公钥的根 R、公共位域 b、消息哈希 m
- 私有输入:具有 N 个位域的 N 个 STARK,以及可选的签名以及参与者索引
- 语句: - 递归 STARK 验证:对于所有 1 \le i \le N,第 i 个提供的 STARK 是此语句的有效 STARK,它使用第 i 个位域以及相同的 R 和 m
- 签名验证:如果提供了签名,请检查它是否是 m 的有效签名,其公钥位于公钥树中由参与者索引定义的位置,该树以 R 为根
- 位域联合:公共位域是 STARK 中所有位域的联合,其中为我们具有单独签名的每个 m 索引填充 1
上面的电路被非正式地描述,以演示递归的工作方式(观察输入如何与输出匹配)。
方法 2) 递归 Halo2(原子累积)
与完全递归相比,计算上更便宜的方法是使用像 原始 Halo 构造 这样的原子累积方案。
这里的方法与完全递归类似,因为我们仍然在 SNARK 内部验证证明,但 Halo 方法对证明者来说更轻量级:Halo 仅在 SNARK 内部实现了验证者的轻量级部分,同时 推迟 任何昂贵的操作。这些操作会被推迟到递归链的末尾。
Halo2-IPA
最初的 Halo 论文是基于 Sonic 算术化方案编写的,但我们可以将该协议调整为基于现代 Plonkish 的方案,并使用 IPA 多项式承诺来执行最终的多项式消失参数。这正是 zcash 使用 halo2 所做的事情,但我们也需要它来支持延迟递归。
请注意,在 halo2 中,验证者最昂贵的操作是验证 IPA 打开。使用 Halo 中的技术,我们可以推迟验证 IPA 打开证明时所需的昂贵的链上 MSM。在每个递归步骤中,我们都会延迟此昂贵的操作,并将其累积到 累加器 中。最后,当我们需要将证明传递给下一个人时,该人必须验证证明和累加器。
此外,我们还需要调整该方案以实现携带证明数据,但幸运的是 “来自累积方案的携带证明数据” 论文提供了一个我们可以用于基准测试的构造。
Halo PCD 电路
现在让我们更深入地了解 Halo PCD 电路的样子。对于本节,我们将考虑验证两个证明的递归电路,本质上允许使用二叉树结构进行 PCD。
该电路接收两个元组 (\pi_0, acc_0, z_0) 和 (\pi_1, acc_1, z_1) 作为输入。其中 (\pi_0, acc_0) 是第一个 IPA 证明及其累加器,而 z_0 对应于电路的有用输入。例如,z_0 可以看作是一个元组 (\sigma_0, b_0),其中 \sigma_0 是一个可选签名,b_0 是一个位域。
请注意,在 Halo2 中,整个证明系统都会简化为单个 IPA 证明。还请注意,证明和累加器都具有相同的形式:它们都是 IPA 证明。
我们的 PCD 电路有两个任务:
- 廉价地验证证明和累加器 (\pi_0, acc_0) 和 (\pi_1 ,acc_1),同时将昂贵的 MSM 操作累积到 acc_{out} 中。
- 给定输入 z_0 和 z_1,执行有用的计算函数 F:
- 如果提供了签名,则验证签名。
- 返回所提供位域的并集。
你可以在下面看到电路的非正式表示:
请注意,在现实生活中,电路可能看起来有所不同。例如,也许电路不输出累加器,它只是检查其有效性,并且累加器是在电路外部计算的。
方法 3) 折叠(拆分累积)
另一方面是最新的折叠工作。折叠允许我们用更简单的 折叠验证器 替换昂贵的链上 SNARK 验证器。这显著降低了递归的证明者的计算开销,因为实际上没有在电路内部进行证明验证。
折叠过程处理对特定结构 \mathcal{S} 的证明 W 和实例 U。原始 Nova 中的 结构 是一组定义 R1CS 关系的矩阵;后来,这在 Hypernova 中推广到 CCS(更高阶的约束),在 Protostar 中推广到多项式方程。证明 是一组满足结构方程的值(即 Nova 中的 R1CS 约束),而 实例 是对证明的承诺以及一些元数据。我们注意到,实际结构并不完全是 R1CS,而是一种更通用的 松弛 R1CS,其中引入了某些误差项。
实际的折叠是一种从l个输入证明W_1,\ldots, W_l计算 折叠证明W_{folded} 的过程,然后从相同的证明计算交叉项T,最后从输入实例U_1,\ldots, U_l和T计算 折叠实例U_{folded}。整个过程以挑战-响应的方式完成,这保证了 W_{folded} 只有在对于每个 i 存在一个满足 U_i 的 W_i 时才满足 U_{folded}。
为了制作 IVC,证明者创建一个电路 \mathcal{S}',该电路既包含折叠过程的最后一步(这不依赖于证明大小),又包含有用的计算 F,以及一些额外的哈希步骤,这些步骤将实例和 IVC 输入-输出绑定在一起。然后,提交到此电路的证明 W',以便创建一个新的实例 U'。在要求要折叠的实例具有相同的结构,即 \mathcal{S}'=\mathcal{S} 之后,可以在 IVC 的下一步中将 U' 与 U 折叠。
折叠方案具有最小的递归开销,但它们也面临着各种开放的研究问题,我们将在下面讨论。
将 Nova 转移到 PCD
原始论文中描述的 Nova 专为 IVC 链状计算而定制。相比之下,签名合并需要一个 PCD 图状结构,其中的节点接受来自其他节点的任意证明,而没有明确的全局顺序。
调整适用于 PCD 的 Nova 需要我们在电路 \mathcal{S} 中引入一个额外的实例-证明对。这将导致更复杂的 S 以及折叠额外对所需的更多约束。
Paranova 项目 先前已提出相同的方法,指出它允许使用二叉树结构进行 PCD。
最小化曲线周期
折叠和递归 Halo2 都要求我们在电路内部计算椭圆曲线运算。这可以使用非本地算术或使用曲线周期来完成。大多数项目都依赖曲线周期,因为非本地算术比普通算术昂贵许多数量级。
然而,使用曲线周期会导致 一个复杂的系统,因为需要在两条曲线上生成证明,并且需要正确地链接和验证它们。
Cyclefold 的最新工作在我们的 PCD 环境中特别有用,因为它可以降低第二条曲线上的复杂性。使用 Cyclefold,第二条曲线仅用于辅助标量乘法,而无需执行任何 IVC/PCD 操作。
哈希公共输入
折叠电路必然包含 IVC 的输入和输出的哈希以及折叠实例。由于链上哈希相对昂贵,我们需要一种进一步压缩输入的方法。
折叠查找
同样,由于二进制分解过于昂贵,我们寻求一种实现查找以加速 OR 运算的方法。问题在于查找变元需要某些多项式方程的支持,而大多数折叠方案不支持开箱即用的此类方程。我们研究了将查找集成到(Hyper)Nova 中的可能方法,同时对定义和证明的影响最小。
证明大小管理
为了执行折叠,聚合器需要每个折叠实例的完整证明。对于 PCD,这使得每个输入实例的证明至少与 PCD 步进函数的证明一样大。在我们的例子中,它是对两个 1 mln 位输入执行 OR 运算的证明,这至少需要 3 mln 位证明,或 12 K 场元素。折叠运算需要多次标量乘法,总计为 10-20K 个证明元素。总而言之,PCD 折叠证明者从两个发送者中的每一个接收 2-3 MB 的数据作为证明。
深入研究签名合并电路
在本节中,我们将深入研究上述所有方法共有的一些与 SNARK 相关的主题。
上述所有方法都具有相似的功能:我们正在处理 验证签名 并且还 计算位域并集 的 SNARK 电路。在本小节中,我们将更详细地讨论在 SNARK 内部执行这些操作。
在 SNARK 内部验证签名
我们需要选择一个易于在 SNARK 内部验证的签名方案。我们假设要签名的消息是恒定大小(约 256 位),是公共值的哈希,并且对于每个聚合过程都不同。鉴于所有方法中的递归开销至少是几次标量乘法,我们可以从以下变体中进行选择:
- Schnorr 类签名:一种简单的基于离散对数的方案,只需要在电路内部进行一次椭圆曲线标量乘法。类似的方案基于 ECDSA 签名。
- 原像证明。在此,签名是密钥 k 知识的证明,该密钥被哈希以获得公钥 K= H(k),其中 H 是一些哈希函数。实际消息是证明过程中上下文的一部分。证明方法选择为签名聚合方法的原生方法,即 Halo-IPA 的 IPA、递归 STARK 的 STARK 和折叠。成本主要由证明方法决定,但也取决于签名中使用的哈希函数,该哈希函数不应太昂贵。
- 加密密钥证明。此方法类似于前一种方法,其中公钥 K 是在密钥 k 上加密某些常量(例如 0)的加密结果,即 K = E_k(0)。实际签名可能是也可能不是加密的结果,例如 FAEST 方案。
虽然签名方案的选择最初看起来很重要,但实际上重要性较低,因为在所有递归 SNARK 构造中,链上 SNARK 验证器控制了该方案的性能。
使用查找的位域并集
获取两个位域并集的过程是一个简单的逻辑运算,但是它不能很好地转换为算术电路的语言。
一种简单的方法是将位域分解为位,然后分别处理每一位,确保两个输入位与输出位匹配。这意味着我们必须花费 O(logd) 个约束,其中 d 是位域的大小。
这似乎是使用查找变元的完美环境,它使我们可以将多个位块放在一起,并为每个块花费一个约束。
考虑一个大小为 2^5 的两个位域的所有可能的 OR 输出的查找表。这意味着我们可以将位域分成五个位的块,并使用查找协议来执行并集。
管理电路大小
重要的是要观察电路的大小如何影响上述方法。电路越大,递归验证它就越痛苦。
还值得注意的是,在许多签名聚合协议中,该协议将首先合并微小的位域,然后再移动到越来越大的位域。因此,如果我们只需要为我们使用的东西付费 就好了:在处理小位域时使用小电路尺寸。
这可以通过 使用多个电路 来实现:由于输出位域的大小是公开的,因此证明者始终可以选择最适合输入位域大小的电路。这在基于树的聚合协议中可以很好地工作,在该协议中,位域大小和证明者是已知的。
另一种方法是 分块证明的语句:而不是处理完整的位域,而是每次处理较小的块,并在需要时生成多个证明。在协议开始时,证明者将处理小电路并生成单个证明,但是随着协议的进行并且位域的增长,证明者将需要为每个位域生成多个证明,因此递归开销将增加。
性能评估
在本节中,我们旨在让你了解所讨论方案的性能预期。
重要的是要注意,在没有完全实现这些方案的情况下获得精确的数据具有挑战性,尤其是在存在尚未解决的问题的情况下。
我们首先在下表中提供概述,然后分别研究每个方案。
Merge 成本 |
MergeVerify 成本 |
通信开销 | |
|---|---|---|---|
| 递归 STARK | 糟糕 | 非常好 | 糟糕 |
| 递归 Halo2 | 还可以 | 还可以 | 良好 |
| 折叠 | 良好 | 还可以 | 非常糟糕 |
性能评估:递归 STARK
虽然在没有实现的情况下很难获得递归 STARK 方案的合理基准,但在本节中,我们将介绍 RISC0 团队提供的基准数据,该团队正在将 STARK 递归用于其他应用程序。
虽然 RISC0 基准肯定有用,但值得指出的是,专门为我们的用例设计的自定义电路将使我们能够调整系统的各种参数(例如,哈希函数、有限域,安全参数等),而实际数字可能会大相径庭。
在附录 B 中,我们提供了一个正在进行中的草案,该草案采用公式化方法来评估递归 STARK 的证明者的性能。
Merge 成本
就 API 而言,在本节中,我们将考虑 签名合并方案 的 Merge() 函数的成本(即将两个位域合并在一起)。
RISC0 证明者当前花费 2.5 秒在电路内部递归验证 2 个 STARK。这有效地允许上述电路中的 N = 2,并启用二进制“证明树”结构,该结构在 PCD 应用程序中很常见。
RISC0 系统旨在实现 100 位的安全性,并且证明者的大部分时间都花费在哈希处理整个证明上。上面的数字来自配备 Nvidia A4000 GPU 的证明者,这是一种验证者通常没有的专用硬件。
RISC0 团队认为,通过进一步优化其 GPU 实现和算法,他们可以在未来几年内将证明者的速度提高多达 4 倍(可能会使 Merge 的成本降至一秒以下)。
RISC0 的电路正在证明 RISC0 VM 指令,而我们的电路正在验证签名和合并位域。通过与 RISC0 团队的讨论,我们认为底层应用程序并不那么重要,因为大型 STARK 验证器电路控制了证明者的性能。
MergeVerify 成本
超级快!几毫秒。
通信开销
STARK 的证明大小约为 300kb(取决于安全参数),这非常大。
性能评估:递归 Halo2
在本节中,我们将考虑大小为 100 万位的参与位域。这意味着可以使用 2^{12} 个字段元素来表示它们。我们估计最终电路的大小约为 d = 2^{16},因为它至少需要处理两个输入位域。
Merge 成本
该方案中的证明者时间是执行有用计算(即,合并位域或验证签名)所花费的时间,以及递归验证所提供的任何证明所花费的时间。
有用计算的证明者时间:
- 签名验证: 200-2000 个 R1CS/(低阶 Plonkish) 门
- 位域并集:
- 纯:2^{21} 门(2 度)用于二进制分解,2^{20} 门用于并集运算。
- 使用查找:每个 8x8 按位 OR 1 个门:120K 个门和大小为 64K 项的表。
递归开销(本质上是 “来自累积方案的携带证明数据” 论文第 5.1 节的算法 \mathbb{P} 的运行时):
- 所有证明和累加器的延迟 IPA 验证(\pi_0, acc_0, \pi_1, acc_1):
- 4 \cdot 2 \cdot logd = 4 \cdot 2 \cdot 16 = 128 ECMULs
- 4 \cdot 2 \cdot logd = 128 ECADDs
- 4 \cdot logd = 64 哈希
最后,让我们计算总递归电路大小:
- 假设一个 8 位的预处理查找表,则位域并集电路可以在 2^{20-8} = 2^{12} 个约束内实现。
- 使用 Jellyfish 的自定义门,每个 ECMUL 需要 300 个 plonkish 约束,每个 poseidon 哈希需要 200 个 plonkish 约束。延迟 IPA 验证电路可以在 51200\approx 2^{16} 个约束内实现。
因此,递归电路大小估计为 2^{16} 个约束。
使用 Pallas/Vesta 曲线,可以在高端桌面上大约 1.6 秒内证明这样的电路。如果我们要使用 GPU,则可以在 0.35 秒内执行证明。
MergeVerify 成本
就 API 而言,签名合并方案 的 MergeVerify() 函数对应于累加器的决策器功能。
决策器需要执行两个 MSM,曲线的每一侧一个。MSM 的大小等于电路的大小,即如果我们使用查找,则为 2^{16}。
使用一台体面的现代笔记本电脑,可以在大约 200 毫秒内执行每个 MSM,或者使用高端 m6i.8xlarge AWS 实例大约在 51 毫秒内执行每个 MSM。
通信开销
Halo 方法的通信开销基本上归结为发送 Halo2 证明和累加器。这是大小的非正式细分:
- Halo2 证明大小:
- 对于每个证明列:
- 承诺(G 点)
- 随机元素的打开值(1 个字段元素)
- IPA 打开证明(2 log n 组元素,1 个字段元素)
- 累加器大小:
- 承诺(G 点)
- 随机元素的打开值(1 个字段元素)
- IPA 打开证明(2 log n 组元素,1 个字段元素)
其中 n 是电路大小(在我们的例子中约为 2^{16})。
总而言之,通信开销取决于电路结构(证明列数)。我们认为实际的通信开销将在 5kb 到 15kb 之间,其中后一个数字是针对具有 13 个证明列的电路。
性能评估:折叠
证明对折叠 PCD 方案的性能进行评估是最具挑战性的任务,这主要是由于围绕折叠和分布式证明者的 PCD 存在未解决的研究问题。
在以下部分中,我们提供了初步评估以启动评估过程。
Merge 成本
Merge 操作由两项任务控制:
- 计算交叉项——大小为 C 的 MSM,电路大小。
- 计算折叠过程的证明的实例——相同大小的 MSM。
所以本质上是 2n 大小的 MSM。
运行有用的计算函数 F 的成本将取决于折叠查找方案的最终效果如何。
MergeVerify 成本
验证折叠的证明是否满足折叠的实例本质上是另一个 n 大小的 MSM。
通信开销
如“证明大小管理”部分所述,我们预计需要发送给下一个证明者的证明大小约为 2-3MB,对于一百万位的位域来说,与其他方法相比,这是巨大的。
未来的工作
我们欢迎对以下问题的贡献:
- 为三种方法中的任何一种方法编写 PCD 电路的详细规范
- 实施三种方法中的任何一种方法,以便我们可以获得更精确的基准
- 解决折叠部分中提出的开放研究问题
- 在以太坊签名聚合拓扑上做更多的工作
如果你有兴趣从事上述工作,请联系我们!
附录 A:在以太坊中使用签名合并方案
考虑一个基于 Gossip 的聚合方案:
聚合协议的开始(签名阶段):
- Alice 使用
Sign()创建一个签名,并将其发送给 Bob。
聚合协议的下一阶段(聚合阶段):
- Bob 使用
Verify()验证签名 - Bob 收到了一堆签名,并使用
Aggregate()创建一个合并的签名 \pi - Bob 将 \pi 发送给 Charlie
聚合协议的下一阶段(合并阶段):
- Charlie 使用
MergeVerify()验证合并签名 - Charlie 收到了一堆合并签名,并使用
Merge()创建一个合并签名 \pi - Charlie 将 \pi 发送给 Dave
[合并阶段重复...]
聚合的最后阶段(发布到区块):
- Dave 将他最好的合并签名 \pi 发送到全局主题(使用
GetSigners()的权重来选择最佳签名) - 提议者 Peter 监控全局主题并找到最佳合并签名
- 他使用
MergeVerify()验证它,并将其放在区块上 - 他使用
GetSigners()将奖励分配给参与的验证者
附录 B:STARK 递归的性能估计
对于给定的安全级别 \lambda,令 \phi{\lambda}(m) 表示验证一个 STARK 所需的哈希调用次数,该 STARK 用于计算对 64 位哈希函数 Rescue/Poseidon 的 m 次调用(它们具有相似的 witness 大小)。那么证明大小等于 32\phi{\lambda}(m) 字节。用于检查单个 STARK 证明的验证电路然后计算 \phi_{\lambda}(m) 个哈希。为了递归 N 个 STARK 并保持验证电路大小不变,我们需要
N\phi_{\lambda}(m) <m
来自 Starkware specification 的图 7 表明 \phi_{100}(m)\leq 150 \log_2 m。因此,我们需要 m 使得 \frac{m}{\log_2 m}>150N。对于 N=2,我们可以选择 m=2^{12} 并且 \phi_{100}(m)\approx 1500。
- 每个 slot 坚持 8192 个签名 post-SSF:如何以及为什么
- 基于格的签名聚合
- 完全递归的 SNARK 电路 - “Play to Earn” 的救星
- Orbit SSF:对 solo-staking 友好的用于 SSF 的验证器集管理
- 具有循环和螺旋终结性的 Vorbit SSF:验证器选择和分配
- 原文链接: ethresear.ch/t/signature...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊:应用层开放思维,不弃核心原则 45 浏览
- 理解区块级访问列表 89 浏览
- 以太坊 2029 Strawmap 傻瓜指南 96 浏览
- 以太坊:构建去极权化的数字庇护所 164 浏览
- Orca Whirlpools 对比 Uniswap V3 — ImmuneBytes 127 浏览
- 十年账户抽象,终获解决 152 浏览
- 争分夺秒:构建以太坊的后量子防御 210 浏览
- Vitalik: 以太坊量子抵抗路线图 200 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 260 浏览
- 介绍 strawmap,一份由 EF 协议推出的概念路线图 299 浏览
- 深入探究 ENSv2 架构 299 浏览
- BLS 签名的微妙之处 183 浏览
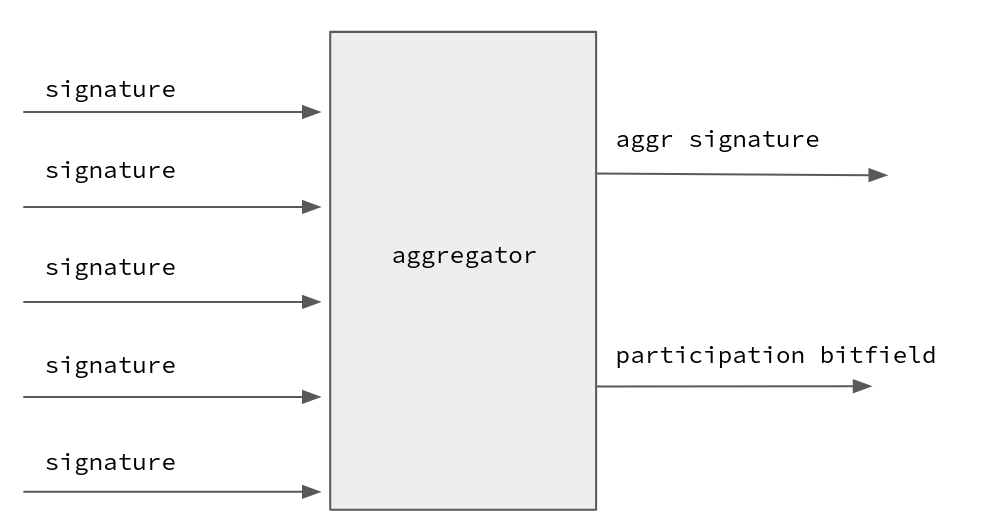 \
image.png992×522 11.9 KB
\
image.png992×522 11.9 KB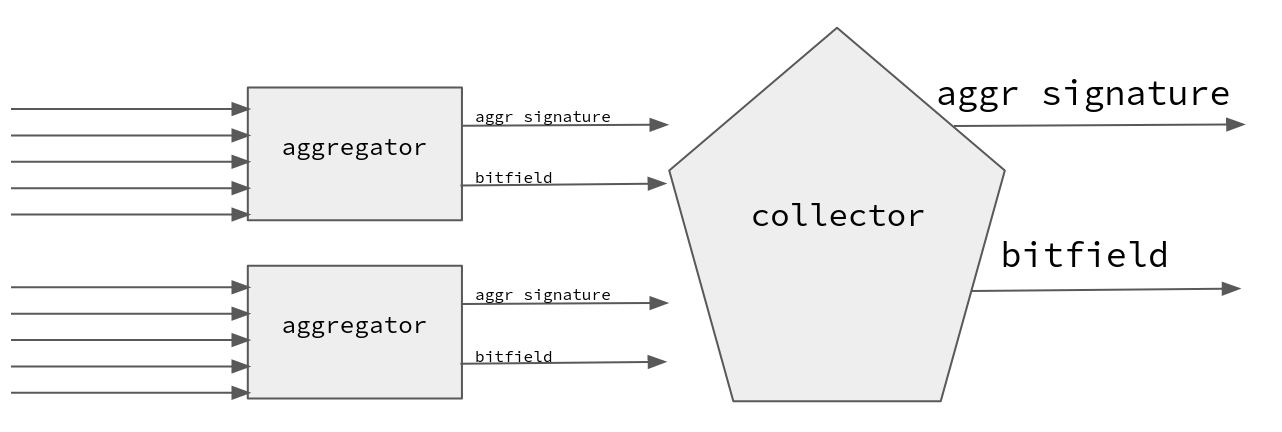 \
image.png1282×432 18.6 KB
\
image.png1282×432 18.6 KB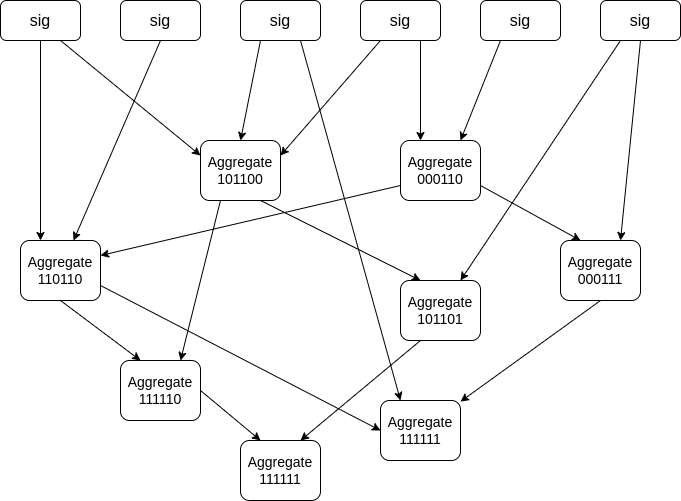 \
681×501 34.4 KB
\
681×501 34.4 KB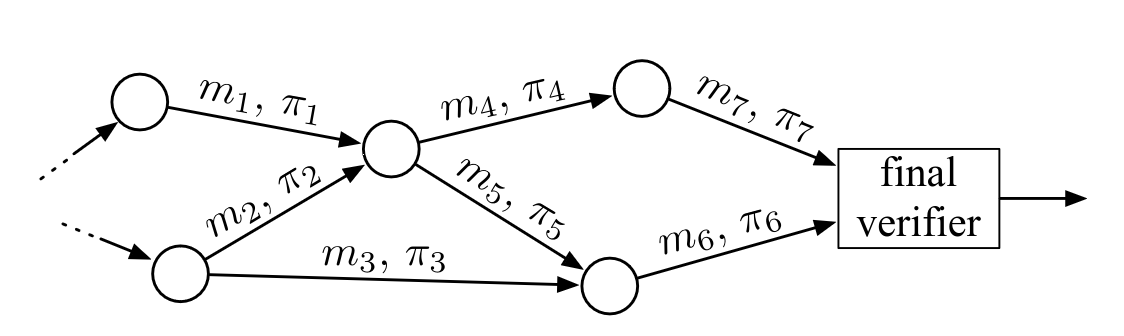 \
image1124×336 20.1 KB
\
image1124×336 20.1 KB \
image.png1364×490 10.9 KB
\
image.png1364×490 10.9 KB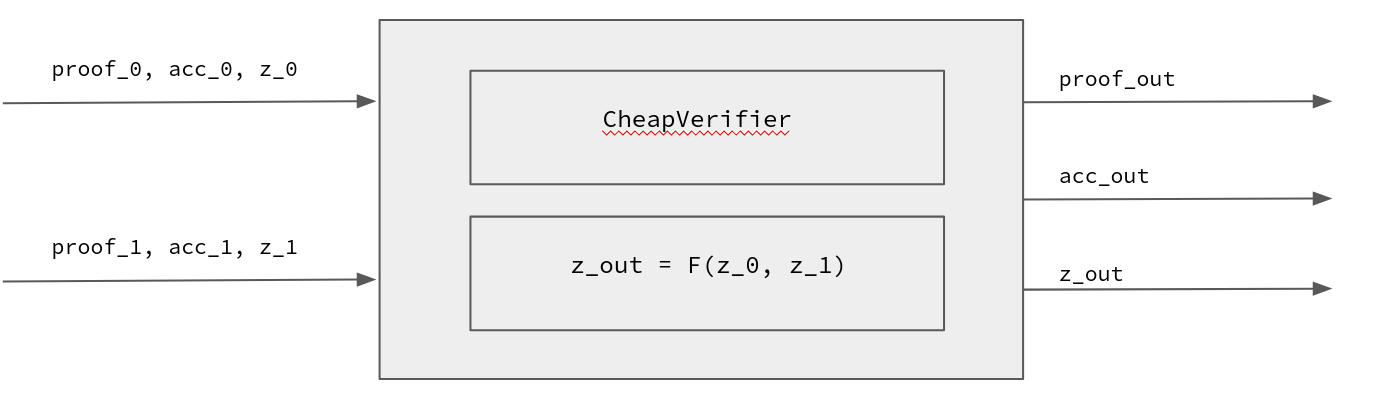 \
image.png1376×400 21.6 KB
\
image.png1376×400 21.6 KB
