问问中本聪…为什么是RIPEMD160和SHA-256？以及为什么是RIPEMD160？

询问中本聪……为什么选择 RIPEMD160 和 SHA-256？以及为什么选择 RIPEMD160？

中本聪过度设计了比特币，使其超级安全

我坚信中本聪是一位技术高超的人，拥有密码学和网络安全研究背景。 因此，比特币组件的技术选择经受住了现代破解的考验。 我不太关心加密货币对我们的社会是好是坏（这由我们的社会、政府和市场来决定），而且我从未拥有过任何比特币，但我确实坐下来思考中本聪创造的惊人的密码学机器。

因此，在 2009 年 1 月 3 日，中本聪启动了这台机器，创造了一个新的数字世界——一个在数学上健全的世界。 它不太关心过去的纸质方法和手写签名——并带来了全新的安全级别。 总的来说，网络安全领域没有多少东西可以在不以某种方式崩溃的情况下运行超过 16 年。 为此，中本聪基本上过度设计了一切，并且知道一个单一的缺陷会使整个基础设施崩溃——并且永远无法恢复。 当你从银行里丢了所有的钱时，你不会再带着你的钱去第二次！

虽然工作量证明方法已被证明是一个重要的弱点（不是因为选择的方法，而是由于能源的浪费），但密码学结构已被证明是完全稳健的。 我明白量子计算机可能会改变这一点，但目前，它是一台已经运行了大约 14 年而没有任何重大故障的引擎。

我们不太可能知道中本聪为什么为比特币选择他们所做的事情，但这可能是计算机科学史上最伟大的突破之一。 为此，中本聪有一个梦想，即任何地方的任何人都只需生成一个随机的 256 位数字（他们的私钥）并将其存储在钱包中。 他们可以创建私钥的 ECDSA 签名以生成公钥，然后对该公钥进行两次哈希以生成公共标识符。 然后，每当使用私钥签署交易时（使用 ECDSA 签名），公共标识符将用于证明这是拥有唯一私钥的人……真是天才！

没有数据库或注册密钥！ 没有 PKI（公钥基础设施）！ 没有数字证书（呸！）。 只有纯粹的密码学、椭圆曲线数学和数字哈希的所有美妙之处！ 哦，还有一个Merkle树和一些区块，只是为了确保它超级值得信赖。

让我们问中本聪一些问题……

但是，有很多问题要问……除了中本聪实际上是谁。 首先是为什么中本聪进行了两次哈希，为什么中本聪选择了 RIPEMD160 而不是 SHA1（SHA1 也具有 160 位的哈希值），以及为什么中本聪同时选择了 SHA2 和 RIPEMD160？ 正如我们将发现的那样，中本聪创造了一些完全过度设计的安全性，但旨在为比特币交易产生有效的解决方案。 在一个我们经常看到最低安全级别的世界里，中本聪真的竭尽全力使比特币（几乎）牢不可破。

因此，在我们开始分析之前，让我们看看如何生成比特币 ID：

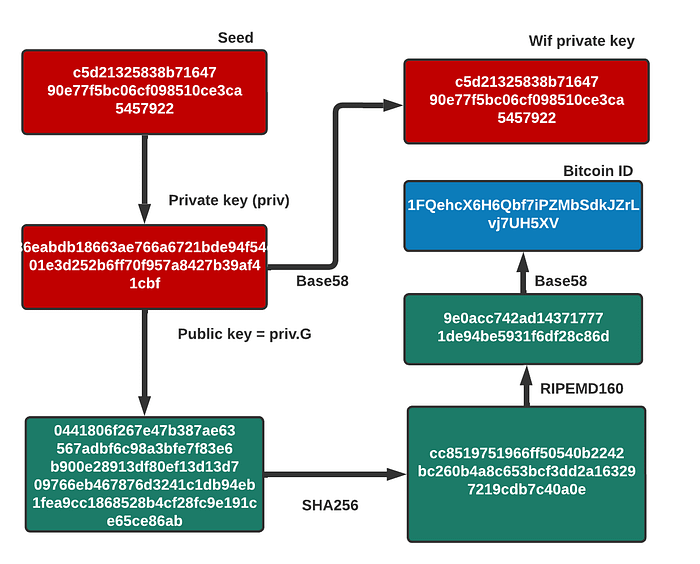
当 Bob 进行比特币交易时，他将使用 ECDSA 使用他的私钥 (priv) 对交易进行签名。 这会产生一个 (r,s) 的签名。 然后可以从中提取 Bob 的公钥，并检查签名。 我们还可以采用 SHA-256 哈希，然后采用 RIPEMD160 哈希来生成钱包 ID，然后检查钱包 ID 是否与签名匹配。

我稍后会解释其中的每个元素，但在我们这样做之前，我们需要看看中本聪选择两个哈希的原因：防止长度扩展攻击。

长度扩展攻击

在我们深入研究所使用的哈希方法之前，让我们看一下哈希的一个问题：长度扩展攻击。 最初的哈希方法通常基于 Merkle-Damgård (MD) 结构。 基于 MD 结构，Ron Rivest 创建了 MD5 哈希方法，并在行业中得到广泛采用。 它的工作原理是采用静态初始化向量 (IV)，然后将其输入到一个单向函数 (f) 中，以及消息块。 我们将此输出输入到下一阶段，依此类推，直到我们到达末尾的消息填充：

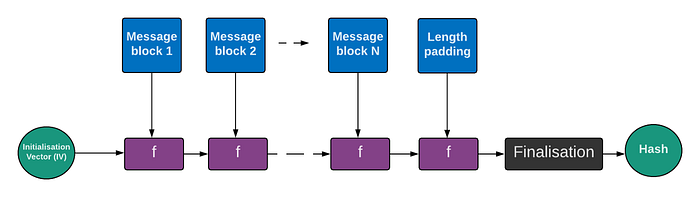
单向函数 (f) 通常会压缩数据，并产生比输入更少的比特。 不幸的是，MD 结构有很多弱点，其中最严重的一个是长度扩展攻击。 通过这种攻击，攻击者 (Eve) 可以获取未知消息的哈希，然后添加其他数据以生成新的有效哈希。

因此，Bob 可以获取他和 Alice 知道的密码的哈希值（“qwerty123”），然后附加一条消息（“hello”）以生成：

H(Password || Message)

其中 “||” 标识将一个字符串附加到另一个字符串。 因此，当 Bob 向 Alice 发送消息时，她将在消息前添加共享密码，并生成相同的哈希值。 这样，Bob 就证明了消息并且他知道秘密密码。 这是一种消息认证码 (MAC)，用于验证 Bob 知道共享密钥和消息。 但是，MD 方法是有缺陷的，因为 Eve 可以获取已知消息的先前哈希值，然后附加一条新消息以生成：

H(Password || Original Message || New Message)

这样，Eve 不知道密码，但仍然可以生成有效的哈希，并将她的消息添加到其中。 代码的概述是 [ here]:

import hashpumpy
import hashlib
import sys
password=b'password'
message= b'message'
addition = b'addition'
if (len(sys.argv)>1):
  password=(sys.argv[1]).encode()
if (len(sys.argv)>2):
  message=(sys.argv[2]).encode()
if (len(sys.argv)>3):
  addition=(sys.argv[3]).encode()

## Compute a previous hash for H(Password || Message)
# 为 H(Password || Message) 计算先前的哈希值
m = hashlib.sha1()
m.update((password+message))
rtn=m.hexdigest()
print ("Previous hash: ",rtn)
## Compute a  hash for H(Password || Message || Addition)
# 计算 H(Password || Message || Addition) 的哈希值
rtn = hashpumpy.hashpump(rtn, message, addition, len(password))
print ("New hash: ",rtn[0])
print ("New message: ",rtn[1])
m = hashlib.sha1()
m.update(password+rtn[1])
rtn=m.hexdigest()
print ("Computing new hash (password+newdata): ",rtn)
#计算新哈希值（密码+新数据）：

文本为 “addition” 的消息 “message” 的示例运行是 [ here]:

Previous hash:  22583ca8f00efff6296b4b571b9c2e1bcf22a99a
New hash:  dd448d0874b738ca1b85bc00e151fbf16393ce4a
New message:  b'message\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00xaddition'Computing new hash (password+newdata):  dd448d0874b738ca1b85bc00e151fbf16393ce4a

在这种情况下，H(Password || “message”) 的哈希值为 ‘22583ca8f00efff6296b4b571b9c2e1bcf22a99a’，Eve 现在可以使用它来生成新的有效哈希，而无需知道密码。 我们可以看到，Eve 可以在消息中生成一些额外的字节，然后添加一条新消息并创建一个有效的哈希。

RIPEMD160 和长度扩展攻击

就其本身而言，RIPEMD160 容易受到长度扩展攻击。 通过这种方式，我们可能会将一个秘密值 (k) 附加到一条已知消息 (m)，然后生成一个消息身份验证码：

ℎ =RIPEMD_160( 𝑚 || 𝑘)

然后，如果我们知道 h 以及 m 和 k 的长度，那么 Eve 就可以轻松地计算出另一个哈希值 h’：

ℎ′=RIPEMD_160( 𝑚 || 𝑝 || 𝑧)

其中 p 定义了一个众所周知的位字符串，并且 Eve 可以选择她想要的任何 z 值。

比特币密钥

那么，为什么中本聪为比特币选择 RIPEMD160 和 SHA-2？

首先，让我们看看私钥和比特币地址是如何创建的。 对于比特币，我们最初为私钥 (s) 生成一个随机的 256 位值，然后创建一个 ECDSA 签名以生成公钥 (vk)：

sk = ecdsa.SigningKey.from_string(s.decode('hex'), curve=ecdsa.SECP256k1)
vk = sk.verifying_key

接下来，我们使用 SHA256 对 ECDSA 公钥进行哈希，然后使用 RIPEM160 再次进行哈希：

ripemd160 = hashlib.new('ripemd160')
ripemd160.update(hashlib.sha256(s.decode('hex')).digest())

最后，我们使用 Base58 将输出转换为公共标识符。

那么，为什么中本聪进行了两次哈希？

嗯，双重哈希当然使比特币地址的生成非常安全，因为几乎不可能将比特币地址反转回公钥，然后再反转回私钥。

那么，为什么中本聪使用 RIPEMD160？

嗯，SHA256 生成一个 256 位的哈希值，而 RIPEMD160 生成一个 160 位的哈希值。 与 SHA-1 一样，160 位的哈希长度不足以完全保护。 但是，在这种情况下，我们具有 SHA-256 的强大安全性，然后应用 RIPEMD160。 160 位的地址使比特币 ID 具有更短的地址。 为此，我们有——在 ‘1’ 标识符之后——33 个 Base58 字符：

186FdYTQQbU7KvaLrsticTgPzv6wfgpc8G

每个 Base58 字符支持大约 5 位，我们最终得到 160 位作为标识符。

因此，这是 160 位的可能原因，但为什么我们使用 RIPEMD160 而不是 SHA-1（SHA-1 也具有 160 位的哈希值）？

编码

RIPEMD 是一种 128 位、160 位、256 位或 320 位的加密哈希函数，由 Hans Dobbertin、Antoon Bosselaers 和 Bart Preneel 创建 [1]。 它用于 TrueCrypt，并且是开源的。 160 位版本被视为 SHA-1 的替代方案，并且是 ISO/IEC 10118 的一部分 [ 理论]。

以下定义了生成比特币密钥的编码 [ here]。 在这种情况下，我们使用 RIPEMD160 哈希来创建公钥：

import ecdsa
import random
import hashlib
b58 = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz'
def privateKeyToWif(key_hex):
    return base58CheckEncode(0x80, key_hex.decode('hex'))

def privateKeyToPublicKey(s):
    sk = ecdsa.SigningKey.from_string(s.decode('hex'), curve=ecdsa.SECP256k1)
    vk = sk.verifying_key
    return ('\04' + sk.verifying_key.to_string()).encode('hex')

def pubKeyToAddr(s):
    ripemd160 = hashlib.new('ripemd160')
    ripemd160.update(hashlib.sha256(s.decode('hex')).digest())
    return base58CheckEncode(0,ripemd160.digest())
def keyToAddr(s):
 return pubKeyToAddr(privateKeyToPublicKey(s))
def base58encode(n):
    result = ''
    while n > 0:
        result = b58[n%58] + result
        n /= 58
    return result
def base58CheckEncode(version, payload):
    s = chr(version) + payload
    checksum = hashlib.sha256(hashlib.sha256(s).digest()).digest()[0:4]
    result = s + checksum
    leadingZeros = countLeadingChars(result, '\0')

    return '1' * leadingZeros + base58encode(base256decode(result))
def base256decode(s):
    result = 0
    for c in s:
        result = result * 256 + ord(c)
    return result
def countLeadingChars(s, ch):
    count = 0
    for c in s:
        if c == ch:
            count += 1
        else:
            break
    return count
private_key = ''.join(['%x' % random.randrange(16) for x in range(0, 64)])
print 'Private key: ',private_key
# 私钥
pubKey = privateKeyToPublicKey(private_key)
print '\nPublic key: ',pubKey
# 公钥
print '\nWif: ',privateKeyToWif(private_key)
print '\nAddress: ',keyToAddr(private_key)
# 地址

一个示例运行是：

Private key:  97c5a919495d4869c11e0872480939c0a81bfe3674767a2e3e2c66490b6113a8

Public key:  04ece141ea5eaa448cd5cabf7f4aeef7a529f5b140fb4e6d2840a142a9325f09801c844db4067b39a1a9cdb96d41f98c6abaf6f9f11cbe4793954b0f08e9e1e951
Wif:  5Jy8PwjawKaJASM2zsracU5cHEQ9FhHtq5cMrTrpKwsPsQjjyeN
Address:  186FdYTQQbU7KvaLrsticTgPzv6wfgpc8G

OpenSSL 已经放弃了对 RIPEMD160 的支持，这会阻止 Hashlib 使用它。 在这种情况下，我们可以使用 Pycryptodome 来实现：

from Crypto.Hash import RIPEMD160
s="Hello"

h = RIPEMD160.new()
h.update(s.encode())
print (h.hexdigest())

RIPEMD160

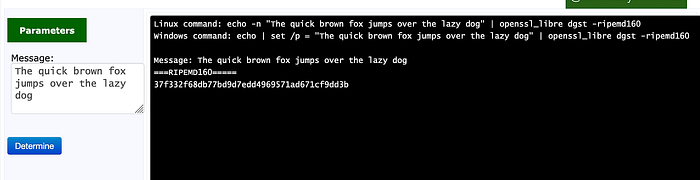
虽然 OpenSSL 已经放弃了 RIPEMD160，但 Libre OpenSSL 仍然支持它。 RIPEMD 的一个测试向量是：

RIPEMD-160("The quick brown fox jumps over the lazy dog") =
 37f332f68db77bd9d7edd4969571ad671cf9dd3b

使用 Libre OpenSSL 的实现如下：

https://asecuritysite.com/hash/ripemd

这是 JavaScript 实现 [ here]:

结论

我很感激这是一篇很长的文章，但它需要如此，才能展示中本聪的比特币方法做得有多好。 对于 RIPEMD160 的选择，中本聪希望尽可能小的公共 ID。 对于 RIPEMD160 而不是 SHA-1，中本聪可能想要混合哈希方法——以防 SHA-1 和 SHA-256 被破解。

中本聪梦想、分析、设计和实施，然后退一步观看机器运转——并且没有为此获得额外的荣誉。 总的来说，比特币远非完美，但它打破了常规，开始了网络安全和信任的重建——以它本应被创建的方式。

Bill Buchanan - 比特币的密码学：密钥的哈希方法

参考文献

[1] Dobbertin, H., Bosselaers, A., & Preneel, B. (1996, February). RIPEMD-160: A strengthened version of RIPEMD. In 国际快速软件加密研讨会(pp. 71–82). Berlin, Heidelberg: Springer Berlin Heidelberg.

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～