零知识证明 - 深入理解ZoKrates
- Star Li
- 发布于 2019-07-24 15:10
- 阅读 18717
2018年 Jacob Eberhardt和Stefan Tai两位德国柏林工业大学博士生,提出了链下计算/链上验证的处理框架,并提供了在以太坊上的整个框架的工具链。链下计算/链上验证的思想很早就有,但是能提供比较完善的工具链的实属难得。目前ZoKrates使用zk-SNARK算法实现零知识证明。
2018年 Jacob Eberhardt和Stefan Tai两位德国柏林工业大学博士生,提出了链下计算/链上验证的处理框架,并提供了在以太坊上的整个框架的工具链。链下计算/链上验证的思想很早就有,但是能提供比较完善的工具链的实属难得。目前ZoKrates使用zk-SNARK算法实现零知识证明。
本文介绍ZoKrates的思想,工具链的使用以及源代码导读。
链下计算/链上验证
传统区块链整个交易或者计算(Tx)的内容都是存储在区块链上,并且每个节点都需要执行整个交易或者计算。ZoKrates将计算移到链下,并生成证明,链上只需要验证证明是否正确,从而确认相应的计算。链下计算/链上验证的方式有一些好处:1)提供隐私的能力 2)降低链上数据存储 3)减少链上的计算量。
传统的区块链和ZoKrates的区别如下图所示:
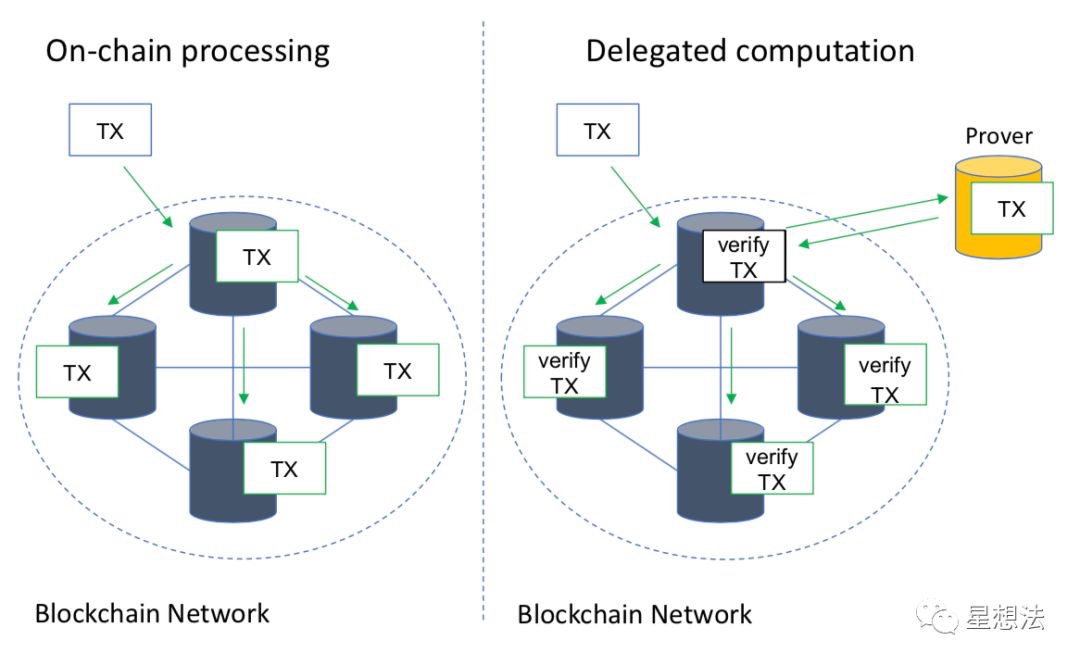
ZoKrates工具链
使用ZoKrates工具链可以很方面地提供某种计算的证明,整个流程由如下的步骤(命令)组成:
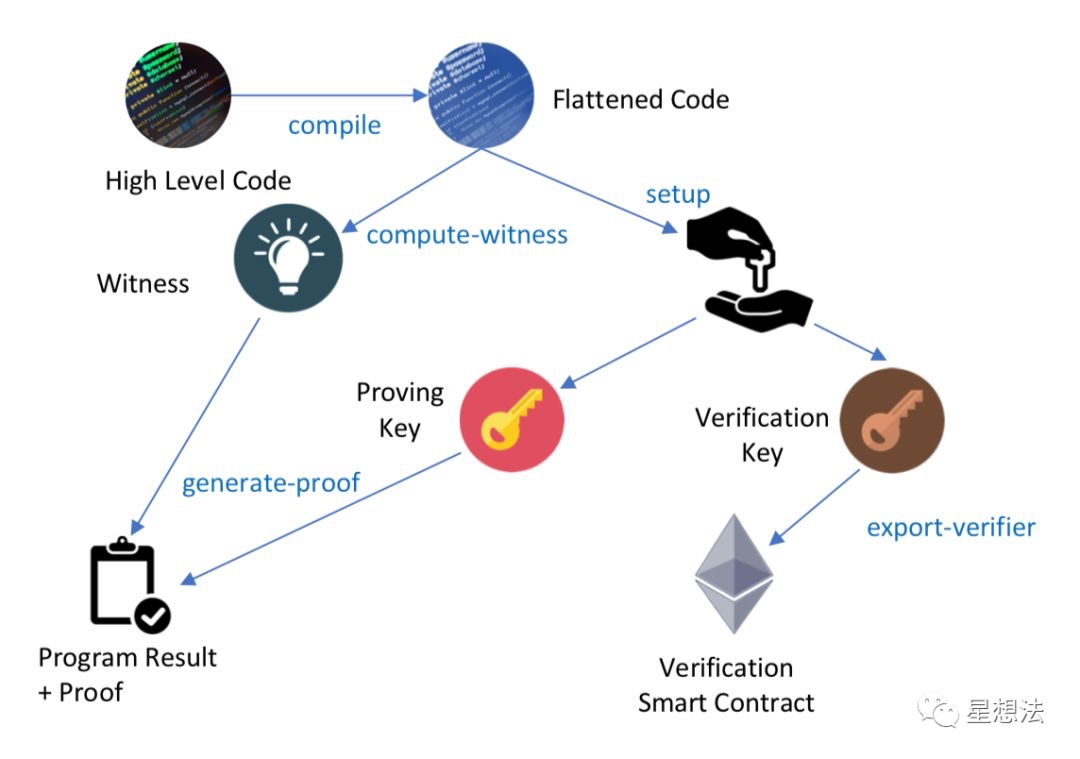
1. compile - 编译电路。对于想证明的计算,需要设计和开发电路。ZoKrates采用DSL(Domain Specific Language)描述电路。ZoKrates也提供了一些常用的电路库(SHA256,椭圆曲线的计算等等)。
2. setup - 设置。对于每个电路,在生成证明之前,必须setup一次,生成CRS。
3. compute-witness - 生成witness。在提供了private/public输入的情况下,ZoKrates自动根据电路计算出对应的witness。
4. generate-proof - 生成证明信息。
5. export-verifier - 导出验证工具。比如在以太坊上,export-verifier可以导出可在以太坊上部署的证明验证合约。
从电路的DSL描述,最后到生成以太坊上的智能合约的流程,如下图:
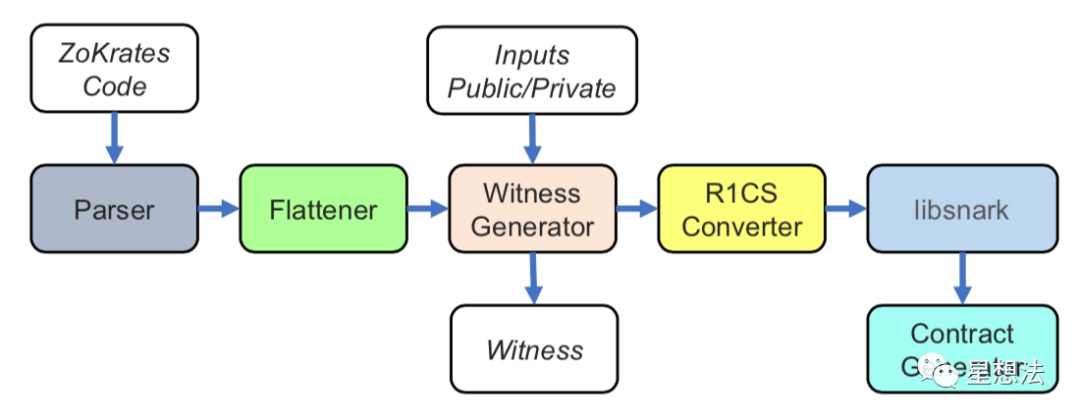
DSL电路示例
ZoKrates给出了详细的电路描述和编译的说明,可以查看链接。
如下的电路是最简单的DSL电路描述,判断a的平方是否等于b,等于返回1,不等于返回0:
def main(private field a, field b) -> (field):
field result = if a * a == b then 1 else 0 fi
return resultfield是DSL电路的基本数据类型。一个field代表一个整数,范围[0, p-1],其中p为大的质数。field前面加上关键词private,说明这个field的数据是private的,属于“witness”。电路的描述文件以.code为后缀。
ZoKrates源代码导读
本文中使用的ZoKrates源代码的最后一个commit信息如下:
commit 87312a55e94055f14f95afeaa2790783d79a1ee5 Author: schaeff thibaut@schaeff.fr Date: Sun Jun 23 13:35:03 2019 +0200
remove invalid test case
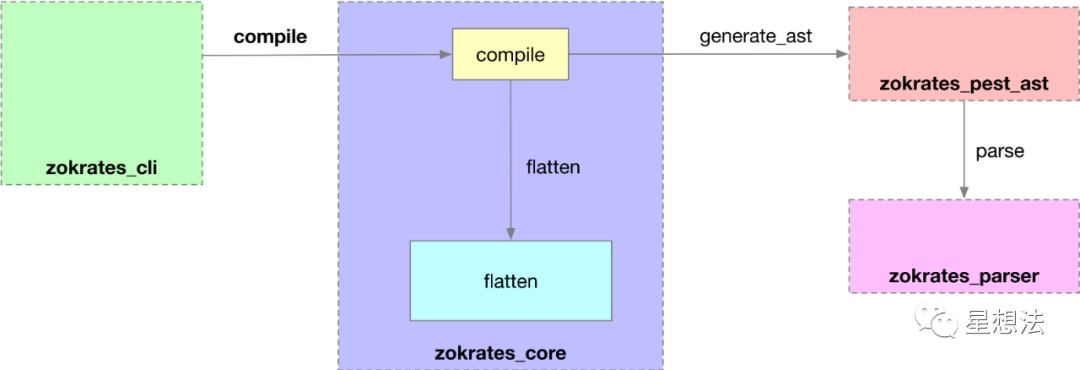
整个ZoKrates的源代码的目录如下图:

zokrates_cli:命令行接口实现。
zokrates_fs_resolver: 文件系统解析。
zokrates_parser: .code电路代码解析。
zokrates_pest_ast: 解析电路为AST(Abstract Syntax Tree)。
zokrates_stdlib: 一些预实现的电路(比如,sha256函数,pedersen hash函数,ecc相关计算)。
zokrates_core: zokrates的核心逻辑代码。解析.code电路,调用bellman相关接口,实现电路的生成,proof的生成和验证。
简单的说,ZoKrates的逻辑分为三部分:CLI代码,电路的解析(pest/ast)以及调用bellman生成电路/证明。以下从CLI命令行为起点,解析逻辑相关的代码。
compile命令
compile命令编译.code描述的电路:
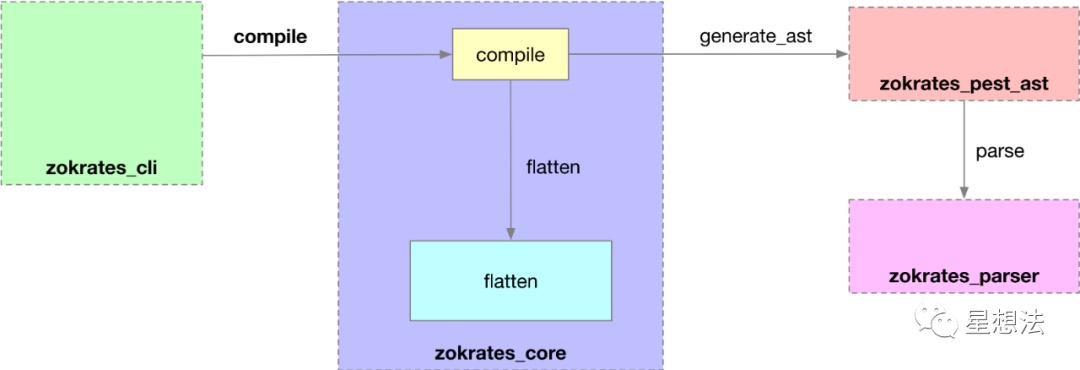
./zokrates compile -i sample.code编译的逻辑在zokrates_core/src/compile.rs模块的compile_aux函数中。
通过zokrates_parser模块解析.code电路。电路程序的语法定义在zokrates_parser/src/zokrates.pest文件中。也就是说,电路程序使用pest库进行语法解析。进行语法解析后,通过zokrates_pest_ast模块生成ast(语法树)。最后再通过flatten模块,将电路“拍平”。最后编译后的程序,用FlatProg表示(定义在zokrates_core/src/flat_absy/mod.rs):
pub struct FlatProg {
/// FlatFunctions of the program
pub functions: Vec>,
}
pub struct FlatFunction {
/// Name of the program
pub id: String,
/// Arguments of the function
pub arguments: Vec,
/// Vector of statements that are executed when running the function
pub statements: Vec>,
/// Typed signature
pub signature: Signature,
}也就是说,一个电路程序由一个个的FlatFunction构成,每个FlatFunction中包含参数以及一系列的FlatStatement(R1CS表达式)。解析完成的电路程序会存放在临时文件中(当前目录下的output文件中)。
setup命令
setup命令生成CRS。
./zokrates setupZoKrates提供几种零知识证明的方案:PGHR13, G16和GM17。默认采用G16的方案。
核心逻辑在zokrates_core/src/proof_system/bn128/g16.rs的setup函数中。
通过zokrates_core/proof_system/utils/bellman模块,调用bellman库中的generate_random_parameters函数生成随机数,并算出对应的CRS数据。注意,在生成CRS数据之前,需要synthesize电路生成R1CS。
compute-witness命令
compute-witness命令,指定输入参数,生成满足电路R1CS限制的所有变量对应的值。如下是示例电路对应的compute-witness的命令,示例电路对应的a为337,b为113569:
./zokrates compute-witness -a 337 113569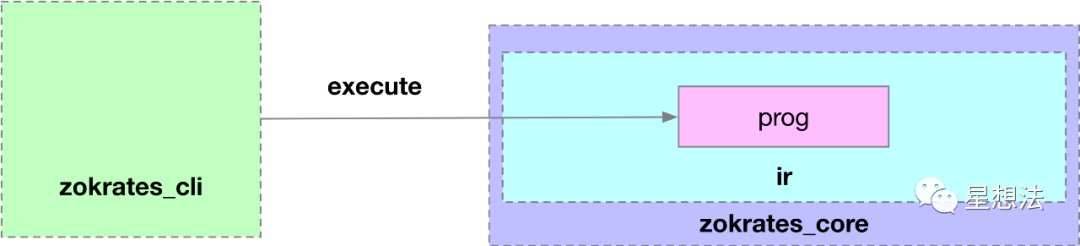
核心逻辑在zokrates_core/src/ir/interpreter.rs的execute函数中。获得满足电路的所有变量的值,就是“执行”一下电路逻辑,记录相应变量的值即可。
generate-proof命令
generate-proof命令,使用compute-witness生成的witness信息,以及setup生成的CRS数据,生成proof证明。
./zokrates generate-proof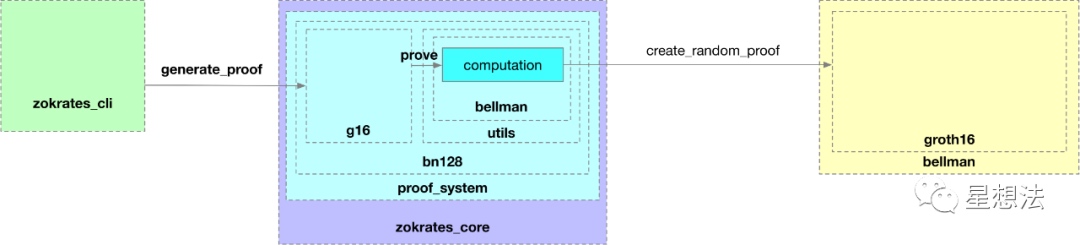
核心逻辑在zokrates_core/src/proof_system/bn128/g16.rs的generate_proof函数中。调用bellman库的create_random_proof生成证明。
export-verifier命令
export-verifier命令,导出以太坊上可以部署的验证证明的智能合约。
./zokrates export-verifier核心逻辑在zokrates_core/src/proof_system/bn128/g16.rs的export_solidity_verifier函数中。在g16.rs中,定义了一个Groth16证明验证的模版程序(其中一部分如下):
function verifyingKey() pure internal returns (VerifyingKey memory vk) {
vk.a = Pairing.G1Point();
vk.b = Pairing.G2Point();
vk.gamma = Pairing.G2Point();
vk.delta = Pairing.G2Point();
vk.gammaABC = new Pairing.G1Point[]();
}这个模版程序定义了一些“宏变量”(vk_a, vk_b, vk_gamma, vk_delta等等)。export-verifier函数,针对当前的电路以及CRS信息,替换相应“宏变量”,生成真实的验证电路的智能合约。
总结:
ZoKrates提出了链下计算/链上验证的处理框架,并提供了在以太坊上的整个框架的工具链。ZoKrates使用zk-SNARK算法实现零知识证明。ZoKrates的工具链,极大地降低了在以太坊上实现链下计算/链上验证的逻辑的门槛。只需要使用DSL语言编写电路,就能使用ZoKrates工具库实现链下计算,同时可以导出以太坊上对应的智能合约,实现对应电路的证明验证。
本文作者 Star Li,他的公众号星想法有很多原创高质量文章,欢迎大家扫码关注。

学习中如遇问题,欢迎到区块链技术问答提问,这里有老师为你解惑。
- 民主事物的再思考:构建共识发现工具 57 浏览
- Zero 链: 技术定位报告 160 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 159 浏览
- 以太坊 2029 Strawmap 傻瓜指南 224 浏览
- 不实的断言:攻破 6 个 zkVMs 157 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 286 浏览
- 零知识编年史:群 233 浏览
- 为比特币的量子抗性研究基于哈希函数的签名方案(一) 259 浏览
- 以太坊执行层优化:状态树与虚拟机 387 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 281 浏览
- 首次 ZK 攻击发生,且出乎意料 290 浏览
- Vitalik: 以太坊量子抵抗路线图 262 浏览

