Switchboard集成：统计数据的隐藏风险

预言机

为了确定上下文，理解两种价格来源之间的区别至关重要：外部数据预言机和链上协议。

外部数据预言机，如 Chainlink、Pyth、Switchboard，通常由一个提供外部数据的提供者网络组成，这些数据以 feed 的形式呈现，同时遵守严格的规则以确保数据被认为是有效的。每个提供者提交他们的观察结果（例如，ETH/USD 价格），预言机系统使用各种方法组合这些提交，从而得出一个最终值。

相比之下，链上来源，如 AMM 池数据、TWAP 或其他，直接源于智能合约，这些合约公开数据供其他协议使用。

预言机网络通常被认为比其链上对应物更安全，因为它们通常更难操纵，但这是有代价的：信任。

信任的架构

现代预言机系统采用各种机制来确保数据的可靠性。去中心化预言机网络不是依赖单一来源，而是聚合来自多个独立数据提供者的信息。这个聚合过程至关重要。在传统金融中，像交易所这样单一的可信实体可能会提供官方价格。在 DeFi 中，任何单个数据源都可能被破坏或仅仅是不正确。通过结合多个来源、财务激励和统计方法来过滤掉异常值，预言机旨在提供稳健、抗操纵的数据 feed。

隐藏的复杂性

虽然预言机解决了将外部数据引入链上的问题，但它们引入了自身的复杂性和潜在的漏洞。预言机数据被处理、聚合和验证的方式可能会产生不易察觉的细微的攻击途径。

在最近的一次审计中，我们发现，表面上合理的数学方法在价格聚合中可能潜藏着重大的漏洞。其中一个问题涉及对统计方法的错误应用，虽然表面上看起来很稳健，但实际上可以被利用。

Switchboard 价格 Feeds

Switchboard 价格 feeds 可以被 permissionlessly 部署，并公开详细的实时信息和/或配置选项，开发者可以使用这些信息来定义定价机制。

价格 feed 管理员可以定义配置参数，例如最大允许方差、陈旧程度和/或提交被认为是有效的所需的最小响应数。这些参数直接影响报告价格的可靠性，并且可以通过 PullFeedAccountData struct 在链上访问。

每个参数都为开发者提供了对准确性要求的精细控制，并发挥着独特的作用：

• max_variance 字段确保只接受具有可接受的统计一致性的提交，从而过滤掉潜在的异常值或操纵企图。
• min_responses 和 min_sample_size 强制要求足够数量的独立预言机提交为每次价格更新做出贡献，从而防止少数潜在被破坏的预言机扭曲结果的情况。
• max_staleness 参数确保价格的新鲜度，这对于快速移动的市场至关重要，在这些市场中，陈旧的数据可能导致重大损失。

为了访问价格，开发者可以读取 submissions 字段，该字段返回 32 个最新的价格提交，或者读取 result 字段，该字段返回当前结果的统计信息：均值、方差、标准差、范围、样本数等。

均值、中位数和标准差

在深入研究漏洞之前，让我们先弄清楚一些对这个问题至关重要的基本统计概念：

均值 (平均值)

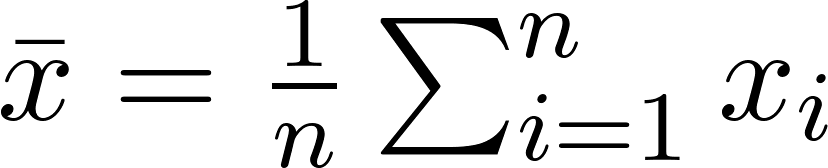
均值是所有值的总和除以值的个数，也称为平均值。

Example:
Prices [100, 102, 104, 106, 108]
Mean = (100 + 102 + 104 + 106 + 108) / 5 = 104

均值平等地考虑每个值，使其对极端值敏感。单个异常值可以显著改变均值，但是样本越多，异常值的影响就越小。

中位数 (中间值)

中位数是将所有数字按顺序排列时的中间值。对于奇数个值，它是中心值。对于偶数个值，它是两个中心值的平均值。

Example:
Prices [100, 102, 104, 106, 108]
Median = 104 (the middle value)

Example with outlier: [100, 102, 104, 106, 500]
Median = 104 (still the middle value, unaffected by the outlier)

中位数忽略极端值，只关注分布的中心。这使得它对操纵更“稳健”。

标准差 (离散程度)

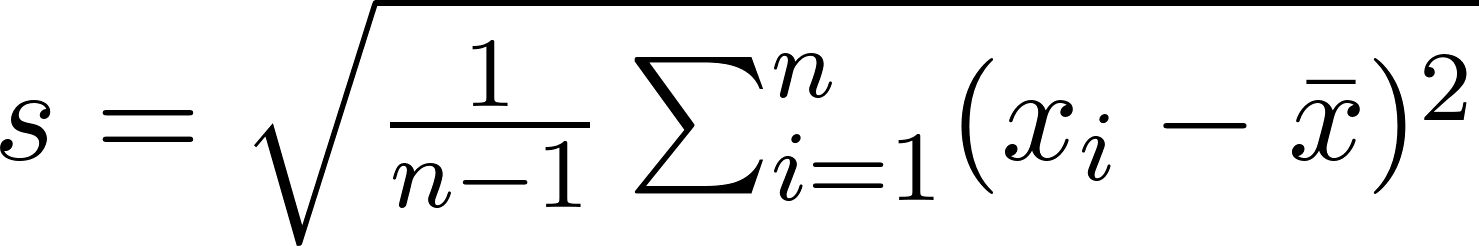
标准差衡量值与均值之间的离散程度。小的标准差意味着值聚集在均值附近；大的标准差表示分散范围广。

Example:
Prices [100, 102, 104, 106, 108]
Mean = 104
Deviations from mean: [-4, -2, 0, 2, 4]
Standard deviation ≈ 2.83

Example with outlier: [100, 102, 104, 106, 200]
Mean = 122.4
Standard deviation ≈ 38.85

至关重要的是，标准差是相对于均值而不是中位数计算的。它衡量所有值与均值的平均距离，使其对异常值高度敏感。当我们关注公式时，尤其如此：我们观察到总和的每一项都是平方的：因此，异常值与均值的距离越高，它就越被夸大。

错误 #1：混淆中位数和标准差

我们观察到标准差被错误地应用到中位数。由于以下原因，这种方法在数学上是不一致的：

标准差衡量的是围绕均值的离散程度，而不是中位数：由此产生的置信区间缺乏可靠的数学基础，并且可能提供关于价格范围的具有误导性的安全感。这些统计数据属于不同的数学框架：中位数是一种对异常值具有抵抗力的稳健统计量，而标准差则不是。这源于标准差公式中的误差项对异常值高度敏感，因为均值和样本点之间的差异是平方的：

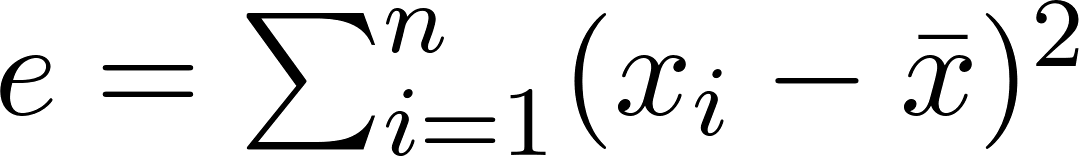
样本点与均值的距离越大，它在最终结果中的权重就越大。

让我们检查一个真实的预言机场景，其中包含五个 ETH 价格提交（以美元计）。

场景 1：正常预言机提交

Submissions: [2000, 2005, 2015, 2020, 2025]
Mean = (2000 + 2005 + 2015 + 2020 + 2025) / 5 = 2,013
Median = 2015 (middle value)
Standard Deviation = 9.27

在这种场景中，中位数和均值非常接近，都准确地表示了真实价格。虽然将标准差应用于中位数在数学上是不正确的，但是如果两个值都足够接近，引入的误差可能可以忽略不计。

场景 2：一个异常值

Submissions: [2000, 2005, 2015, 2020, 2200] (Attacker submits an extreme value: 2025 is replaced by 2200)

Mean = (2000 + 2005 + 2015 + 2020 + 2200) / 5 = 2048 (Shifted by approximately 2%)
Median = 2015 (Still the middle value, demonstrating robustness)
Standard Deviation = 84.3 (Massively inflated)

尽管中位数成功地识别了 2015 的真实市场价格，但标准差计算被中位数忽略的同一异常值破坏了。这造成了根本上的不一致：价格估计是准确的，但是不确定性范围变得毫无意义。

这种场景是我们在整个审查过程中影响最大的场景，因为该实现将标准差用作终止开关：如果该值大于允许的最大值，则预言机将恢复。这允许控制发布者的攻击者报告足够高的价格来 DoS 预言机，这反过来会 DoS 市场，从而阻止清算或提款，直到问题解决。虽然使用中位数来防止此类事件的想法是有效的，但是标准差的使用取消了所需的结果。

场景 3：附加提交

让我们考虑一个中位数可能更容易受到操纵的特定场景：

Submissions: [1995, 2000, 2005, 2015, 2020, 2025] (Attacker submits an additional value)
Mean = (1995 + 2000 + 2005 + 2015 + 2020 + 2025) / 6 = 2010 (Shifted by approximately 0.1%)
Median = 2007.5 (Shifted by approximately 0.5%)
Standard Deviation = 10.80

此场景表明，中位数并非普遍比均值更稳健。当攻击者可以添加新的提交而不是替换现有的提交时，中位数的漏洞取决于样本大小和分布。对于小的偶数样本，策略性地放置异常值可能会比均值更显着地改变中位数（在极少数情况下）。

错误 #2：无效的分布假设

我们还观察到置信区间的错误应用，导致对价格的错误假设。然后，该区间用于计算价格边界 [p - c; p + c]，其中 p 是中位数价格，c 是置信区间。

置信区间是一个值范围，提供了一个估计，即总体参数（如均值或比例）可能落在何处：

• 它表示为一个区间（例如，95% 置信区间：45 到 55）
• 置信水平（通常为 90%、95% 或 99%）告诉我们，如果我们多次重复抽样过程，此类区间包含真实参数的频率
• 95% 置信区间意味着，如果我们从不同的样本构建 100 个此类区间，则大约 95 个区间将包含真实的总体参数

置信区间被广泛用于科学研究中，以报告实验和研究的结果。研究人员不是只报告点估计，而是提供置信区间来显示测量的精度和不确定性。

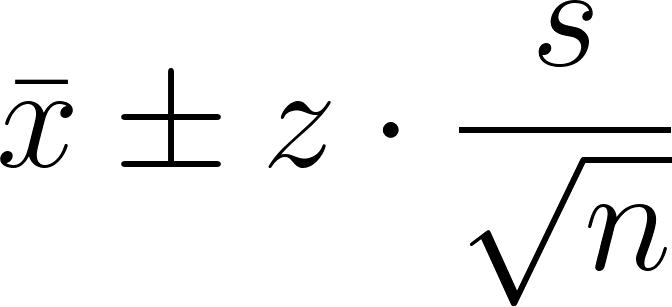
Z 是所需置信水平的临界 Z 值（例如，95% 时为 1.96），s 是标准差，n 是样本大小。这是关于使用样本来估计总体均值，并表示该估计的不确定性。假设你获取了 100 名学生的成绩样本，然后进行计算：

• 样本均值：x̄ = 72

• 样本标准差：s = 8

那么95% 置信区间是：那么95% 置信区间是：

x̄ ± z · (s / √n) = 72 ± 1.96 · (8 / √100) = 72 ± 1.568

因此，该区间是 [70.43, 73.57]

回到我们的预言机，这隐含地假设：

• 预言机价格提交遵循正态分布。
• 样本大小足以应用中心极限定理。
• 提交是独立且同分布的。

正态分布假设有效的典型阈值为 n ≥ 30。对于样本数量低于该值的 feeds，使用置信区间会失去统计意义，这对于大多数 Switchboard feeds 来说都是如此。

我们发现，使用此统计工具将允许攻击者轻松操纵价格边界。根据操作，估计的下限或上限用作操作价格：目的是确保始终有利于协议。

然而，正如场景 2 中所证明的，标准差计算的二次性质使其对小样本量的异常值特别敏感。每个偏差项在公式中都是平方的，因此极端值具有指数级更大的影响（2 倍异常值的影响变为 4 倍，3 倍变为 9 倍，等等）。

这种数学性质意味着单个恶意发布者可以显著提高标准差，从而扩大置信区间，并可能操纵协议使用的价格边界。在极端情况下，这可能会导致强制清算等场景。

以下代码段说明了所有问题：

fn get_oracle_price(
    result: &OracleResult,
    max_uncertainty_bps: u32,
) -> Result<(i128, i128), &'static str> {
    let median = result.median_price;
    // Issue #1: No sample size validation - assumes normal distribution regardless
    // 问题 #1：没有样本大小验证 - 无论如何都假设正态分布
    // Issue #2: Mixing median with standard deviation (mathematically incorrect)
    // 问题 #2：将中位数与标准差混合（数学上不正确）
    let confidence_interval = result.std_dev * 196 / 100; // 1.96 multiplier
    // 1.96 乘数

    // Issue #3: Check uncertainty derived from std dev against a limit, allowing for easy DoS
    // 问题 #3：根据限制检查从标准差导出的不确定性，从而可以轻松进行 DoS
    let uncertainty_pct = (confidence_interval * 10000) / median;
    if uncertainty_pct >= max_uncertainty_bps as i128 {
        return Err("Price uncertainty exceeds maximum allowed");
        // 返回错误：“价格不确定性超过允许的最大值”
    }

    // Issue #4: Compute min/max bounds allowing for price manipulation (bounded by the uncertainty check)
    // 问题 #4：计算允许价格操纵的最小/最大界限（受不确定性检查的限制）
    let min_price = median - confidence_interval;
    let max_price = median + confidence_interval;

    Ok((min_price, max_price))
}

‍

替代方法

考虑到预言机环境的限制（非正态分布、小样本量以及对异常值抵抗力的需求），我们可以探索更合适的统计方法来处理价格不确定性。这些约束要求使用稳健的统计方法，无论分布假设如何，都能保持其有效性，并且即使在单个数据点被破坏或操纵时，也能保持稳定。

最小和最大价格

Switchboard feeds 返回一个 submissions 字段，其中包含所有单独的价格提交。可以使用多种定义价格范围的替代方法：

1. 使用中位数位置 n-1 和 n+1 的提交。这些值很难操纵，因为过度操纵它们会导致它们的位置与 n-2 或 n+2 提交交换，我们可以假设这些提交仍然非常接近真实价格。
2. 使用 MAD（中位数绝对偏差），这是一种类似于标准差的度量，但适用于中位数并且对异常值具有抵抗力。然后可以对其进行调整，以用于围绕均值构建边界。

不确定性阈值

中位数绝对偏差 (MAD)是一种对异常值具有弹性的统计离散程度度量。然后可以将该测量值与阈值进行比较，该阈值应根据analyzed 资产的波动率来确定：

1. 稳定币： 以非常稳定的价格为特征。
2. BTC、ETH、Altcoins：通常在市场高波动期间不如 memecoins 波动。
3. 其他（例如，Memecoins）：表现出非常高的波动。

异常值检测和过滤

在计算价格范围或不确定性阈值之前，应识别出明显的异常值提交并将其从计算中排除。MAD 可用作稳健的异常值检测机制：

1. 从所有提交计算初始 MAD
2. 将异常值识别为符合以下条件的提交：|submission - median| > k × MAD
3. 删除异常值并从清理后的数据集重新计算中位数和 MAD
4. 使用清理后的数据应用价格范围

‍

结论

我们探索的漏洞揭示了现代 DeFi 中的一个重要挑战：随着协议变得越来越复杂，新的攻击媒介可能会从细微的统计不一致中出现。中位数与标准差混合的特定案例表明，数学上合理的各个组件在组合时可能会产生安全问题。

随着 DeFi 的不断成熟，统计学、密码学和经济学的交叉点将需要跨学科的专业知识。理解这些细微的相互作用是构建下一代弹性金融基础设施的关键。

如果你的协议使用预言机并依赖于统计过滤、置信范围或聚合逻辑，那么值得对该层给予额外的关注。这些不仅仅是边缘情况，它们是我们看到的成熟协议中常见的故障模式。好消息是：使用正确的视角，它们通常很容易在成为实际问题之前被发现和修复。

需要审查你的预言机逻辑或聚合层吗？请求报价以开始与我们的团队合作。我们专注于那些在标准测试中不会出现但在真实对抗条件下很重要的漏洞。

• 原文链接： adevarlabs.com/blog/swit...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～