Solana 上浮点运算的一种优雅替代方案
- Adevar labs
- 发布于 2025-08-01 20:19
- 阅读 838
本文探讨了在Solana区块链上构建去中心化借贷协议SolVault时,使用浮点数计算清算惩罚所面临的确定性问题。由于浮点数在不同硬件架构上可能产生不同的结果,违反了区块链的确定性原则。文章提出使用泰勒级数近似法作为替代方案,以实现安全、确定且性能高效的清算惩罚计算,从而保障协议的偿付能力和安全性。
场景:SolVault 的抵押品风险定价
假设你正在构建 SolVault,一个在 Solana 上的去中心化借贷协议。你的协议需要计算清算罚金,这些罚金会根据不同抵押品类型的风险进行调整。风险越高的资产需要更高的罚金,以保护协议。
以下是它的工作原理:
- 用户存入各种代币作为抵押品进行借款
- 每种抵押品类型都有一个基于波动性和流动性的风险评分
- 清算罚金随着风险呈指数级增长,以阻止冒险行为
- 罚金公式确保协议在市场压力期间的偿付能力
挑战在于使用基于风险的模型计算清算罚金:
liquidation_penalty = min_penalty × risk_multiplier^(volatility_score)这种指数关系产生了适当的激励。例如:
- 低风险资产(稳定币):最低罚金
- 中等风险资产(SOL、ETH):适度罚金
- 高风险资产(小市值币):显著罚金
- 指数曲线确保罚金随着风险适当调整
当 risk_multiplier 为 1.5 且 volatility_score 为 3.0 时,罚金乘数为 1.5^3.0 = 3.375×,使罚金为最低罚金的 3.375 倍。
浮点数的困境
自然的实现方式是使用 Rust 的 powf 函数:
pub fn calculate_liquidation_penalty_v1(
asset_config: &AssetConfig,
market_conditions: &MarketConditions,
) -> f64 {
let base_penalty = asset_config.min_penalty_percent;
let risk_factor = asset_config.risk_multiplier;
let volatility = market_conditions.calculate_volatility_score();
// Exponential scaling based on current volatility
// 基于当前波动性的指数缩放
let penalty_multiplier = risk_factor.powf(volatility);
let final_penalty = base_penalty * penalty_multiplier;
// Cap at maximum allowed penalty
// 限制在最大允许罚金
final_penalty.min(asset_config.max_penalty_percent)
}虽然这在测试中完美运行,但它有一个微妙的问题:powf 函数在不同的硬件架构上可能会返回略有不同的结果。 Rust 文档指出,精度可能会相差大约 10-16,这可能看起来微不足道,但如果在 SVM 中以相同的方式实现,它们可能会违反 Solana 对确定性执行的要求。
确定性:区块链不可打破的约定
要理解为什么浮点数运算在链上如此危险,首先必须理解确定性这一不容置疑的原则。在计算机科学中,确定性 算法是指在给定特定输入的情况下,总是产生相同输出并经过相同状态序列的算法。在区块链的背景下,这一原则被提升为不可打破的约定。它规定,去中心化网络中的每个验证者在处理同一笔交易时,必须得出完全相同的结果状态。
一个强大的区块链心理模型是分布式确定性状态机的模型。整个账本的当前状态、所有账户余额、所有存储的数据,都是一个巨大的、达成共识的状态。交易是一种输入,它导致机器转换到新的状态。为了使网络保持共识,每个节点必须独立地计算这种状态转换,并得出相同的结果。如果一个节点计算出新的账户余额为 100,而另一个节点计算出为 101,则共识就会被打破。该链无法继续进行,因为没有单一的事实来源。
为什么浮点数会打破约定
浮点数与确定性背道而驰。 IEEE 754 浮点算术标准虽然无处不在,但并不保证在不同的硬件架构,甚至同一编译器或软件库的不同版本之间,产生逐位相同的的结果。CPU 的浮点单元 (FPU) 的实现方式或 LLVM 编译器(Solana 使用的编译器)处理操作的方式的微小差异都可能导致精度和舍入方面的细微差异。
在一个验证者的 Intel CPU 上产生 1.000000001,而在另一个验证者的 AMD CPU 上产生 1.000000002 的计算表示共识失败。虽然这种差异看起来很小,但在一个建立在加密确定性之上的系统中,不存在“足够接近”的概念。输出必须完全相同。值得庆幸的是,在 Solana 上,所有浮点运算都在所有节点上以相同的方式进行模拟,因此,消除了打破共识的风险。但是,由于这种模拟,性能会受到很大影响。
Solana 的官方立场和性能损失
Solana 文档警告不要使用浮点数,并指出链上程序仅支持 Rust 浮点运算的有限子集。任何尝试使用不支持的运算都会在部署时导致“无法解析的符号错误”。
更重要的是,即使是支持的浮点运算也会带来显着的性能损失。 由于它们不是以原生方式处理的,必须通过 LLVM 的浮点内置函数在软件中进行模拟,因此它们比基于整数的运算消耗更多的计算单元 (CU)。
开发人员一直在与每笔交易 200,000 CU 的计算预算作斗争,选择低效的运算会限制程序的功能。
性能差异并非微不足道。如表 1 所示,根据 Solana 程序库数学测试,基本的浮点运算可能比等效的 u64 运算贵 20 多倍。
表 1:计算单元成本:Solana 上的整数运算与浮点运算
Solana 指令成本表
| 操作 | u64 指令 | f32 指令 | 成本乘数 (f32/u64) |
|---|---|---|---|
| 乘法 | 8 | 176 | 22x |
| 除法 | 9 | 219 | ~24x |
| 数据来源:Solana 官方文档和性能测试。 |
该表显示,使用浮点数效率极低,消耗了交易可用计算预算中不成比例的一部分。
DeFi 困境:清算风险案例研究
回到我们的 SolVault
liquidation_penalty = min_penalty × risk_multiplier.powf(volatility_score)在此公式中:
- min_penalty 是基本清算罚金(例如,5%)
- risk_multiplier 是一个像 1.5 这样的值,表示此资产的风险比基线高多少
- volatility_score 是一个基于当前市场条件的 1 到 5 之间的动态值
- 结果决定了在清算期间扣押借款人多少抵押品作为罚金
此计算使用 powf,将由处理清算交易的每个 Solana 验证者独立执行。
不变量检查:协议的安全网
强大的借贷协议建立在称为“不变量”的数学断言的基础上。 这些是在每笔交易结束时必须保持为真的检查,以确保协议的偿付能力和逻辑一致性。 清算的关键不变量是:
total_collateral_value >= total_debt_value * min_collateral_ratio这确保了协议保持足够的超额抵押。 此外,清算交易必须满足:
penalty_collected + debt_repaid <= collateral_seized_value
如果这些检查失败,程序将设计为 panic 并回滚交易。 这是一种安全机制,可防止协议抵押不足或允许不公平的清算。
触发器:被一个 Lamport 夺走的生命
这里 powf 的非确定性造成了灾难。 考虑一个波动性资产,具有:
- risk_multiplier = 1.8
- volatility_score = 3.2
当不同的验证者计算 1.8^3.2 时,有些可能会得到 4.7829672… 8,而另一些验证者由于其浮点硬件或软件堆栈的细微差异,计算出 4.7829672… 9。 请注意,一个值以 8 结尾,另一个值以 9 结尾。
现在想象一个关键的清算场景:
- 一个拥有 1,000,000 lamports 抵押品的位置需要清算
- 需要偿还的债务是 700,000 lamports
- 一个验证者计算出 penalty = 47,829 lamports
- 另一个验证者计算出 penalty = 47,830 lamports (高 1 lamport)
当清算人试图准确扣押 747,829 lamports(债务 + 罚金)时,该交易在某些验证者上成功,但在另一些验证者上失败,因为罚金计算为 47,830。 不变量检查 penalty_collected + debt_repaid <= collateral_seized_value 失败了 1 lamport。
级联效应
其后果是直接的和严重的:程序 panic,并且清算被回滚。 但这不仅仅是一笔失败的交易:
-
清算僵局:如果由于非确定性计算而无法清算该头寸,它将保留在系统中,并且可能随着市场状况的恶化而进一步资不抵债。
-
协议破产:由于无法清算高风险头寸,协议会累积坏账。
-
预言机漏洞利用:老练的攻击者可能会通过制作在某些验证者上“无法清算”的头寸来利用非确定性,从而在受到清算保护的同时操纵系统。
-
传染风险:其他依赖 SolVault 进行借贷或接受其收据代币作为抵押品的协议开始以有关协议偿付能力的错误假设进行运营。
安全港:使用泰勒级数进行确定性近似
鉴于 powf 的明显危险,开发人员需要一种安全且确定性的替代方案来计算分数幂。 虽然大多数链上数学的标准是使用像 spl-math 这样的定点库,但它们的内置幂函数(如 checked_pow)通常需要整数指数,从而在工具方面留下了空白以用于分数指数。
解决方案不在于找到 powf 的完美复制品,而在于使用确定性的近似值。 其中一种特别有效的方法是泰勒级数展开。
使用多项式进行逼近
泰勒级数的核心思想是用一个简单的确定性多项式来近似一个复杂的非线性函数,在本例中是 xy。 多项式只是具有整数幂的项的总和,可以使用仅加、减和乘的基本算术运算来计算。 这些是可以链上使用定点数学以确定性和有效方式执行的运算。
对于函数 f(x)=xy,围绕 x=1 展开的泰勒级数提供了一个极好的近似值,特别是当 x 接近 1 时,这在 DeFi 中很常见,用于表示小的增长因子(例如,1.001)。
可视化解决方案的安全性
对这种近似方法的分析揭示了它对链上环境的适用性。 以下图表对函数 xy 进行了建模,说明了泰勒级数近似相对于 DeFi 相关领域的精确数学函数的行为:范围为 [1, 1.1] 的底数 x(增长因子)和范围为 的指数 y(时间/费用因子)。
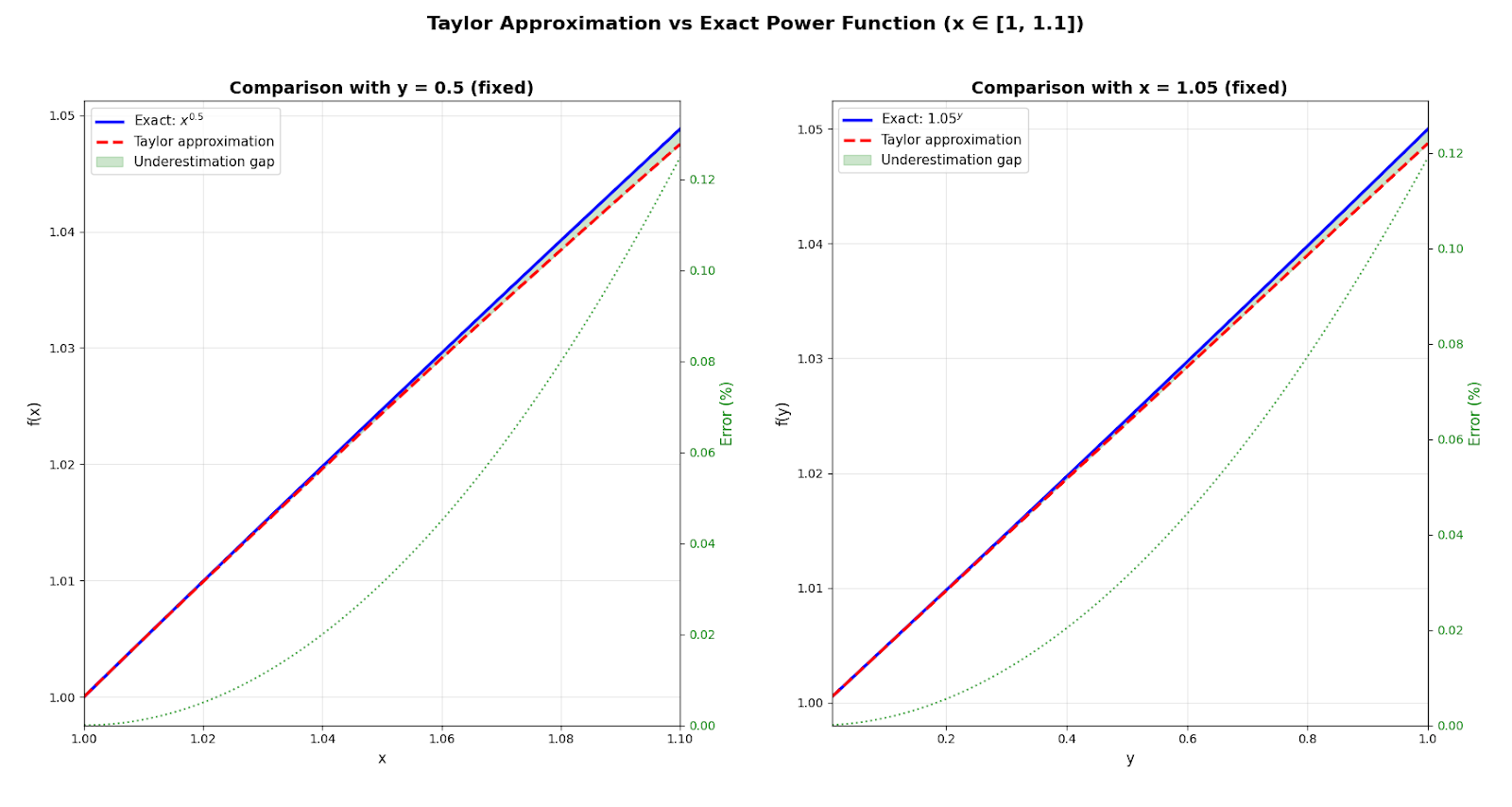
图 1:固定指数(左)和固定底数(右)的泰勒近似(红色)与精确幂函数(蓝色)的比较。 请注意持续的“低估差距”。
如图 1 所示,泰勒近似值(橙色线)紧密跟踪精确值(蓝色线)。 更重要的是,它始终保持在精确值以下。 这种“低估差距”不是缺陷; 它是该近似值最关键的安全功能。
误差热图提供了此行为在整个感兴趣域中的全面视图。
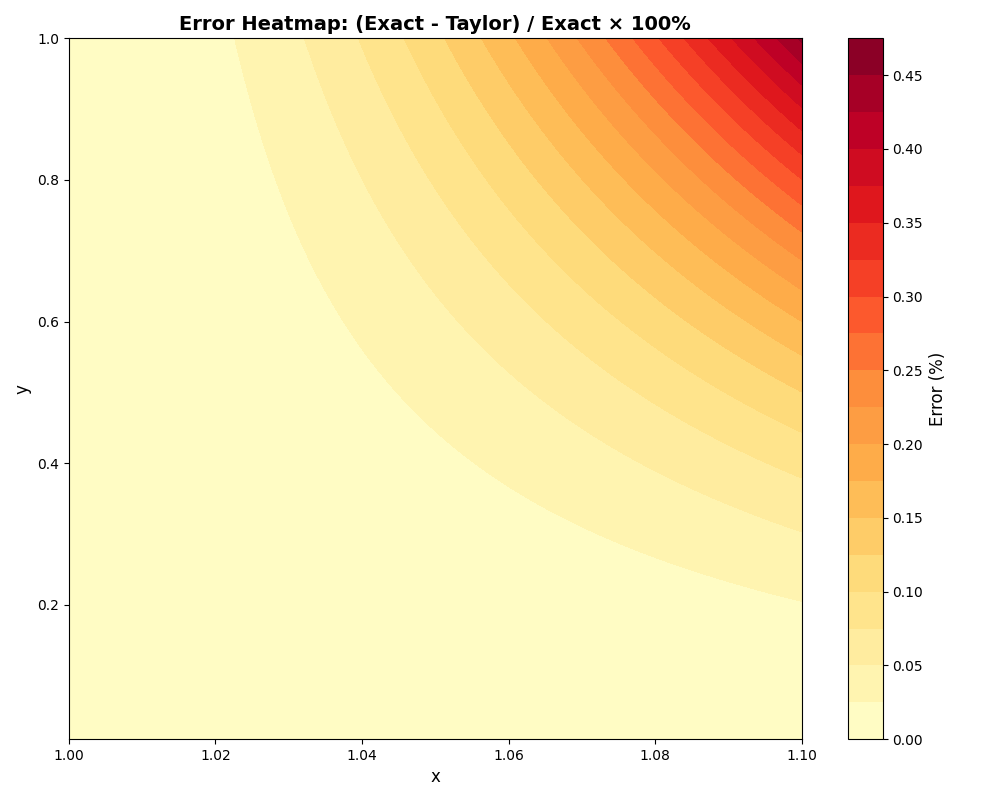
图 2:可视化泰勒近似值相对误差的热图。
图 2 中的热图可视化了近似值的百分比误差。 整个地图都以红色阴影(表示负误差)表明该近似值始终低估真实值。 误差也是有界且可预测的,在此域内的最大误差约为 0.45%,平均误差仅为 0.05%。
这种持续的低估代表了“安全失败”的慎重选择。 在金融软件中,主要有两种类型的错误:损害协议的错误和损害用户的错误。
- 过度贷记用户(例如,给予他们过多的收益)会耗尽协议的资金,从而损害协议。 这可能导致破产,这种失败会影响所有用户。
- 贷记不足用户(例如,给予他们略微较少的收益)对该个人用户不利,但可以保护整个系统的完整性和偿付能力。
通过保证它永远不会过度贷记用户的收益,泰勒级数近似系统地优先考虑协议的偿付能力,而不是完美的用户级别精度。 这将近似值从简单的数学工具转变为为对抗性链上环境量身定制的强大的风险管理策略。 它鼓励开发人员进行范式转变:不要寻求完美复制链下数学,而是应该设计可证明安全的近似值,这些近似值符合协议的特定风险状况和可接受的误差范围。
结论
一个简单的一行代码解决方案来解决复杂的数学问题的诱惑是强大的。 然而,在区块链上,这种简单性可能具有欺骗性和危险性。 浮点数和依赖于它们的函数(如 powf)是不安全的,并且会产生显着的性能损失。 Solana 的开发人员在选择数学工具时必须慎重且持高度怀疑态度。 默认方法必须始终是基于整数的定点数学。 对于更复杂的函数(如分数指数),前进的道路不是寻求完美复制链下行为,而是设计和实现可证明安全的近似值,例如泰勒级数。 此方法提供的结果不仅是确定性和高效的,而且还采用了“安全失败”属性进行工程设计,该属性优先考虑协议的偿付能力和安全性。
最终,构建强大的系统等同于构建可预测的系统。 SVM 的约束不是要规避的限制; 它们是实现信任、安全性和可靠性(拥有实际价值的去中心化应用程序)的非常重要的功能。 在 Adevar Labs,我们将数学视为安全边界。 如果你依赖细微的近似值、定点算术或自定义不变量,那么值得对该逻辑进行审查。
安全发布!
参考文献
-
确定性算法 - 维基百科,访问于 2025 年 7 月 2 日
-
确定性在区块链中意味着什么? - Nervos Network,访问于 2025 年 7 月 2 日
-
限制 | Solana,访问于 2025 年 7 月 2 日
-
Solana 和 Rust 中的算术和基本类型 - RareSkills,访问于 2025 年 7 月 2 日
-
Solana 算术:构建金融应用程序的最佳实践 - Helius,访问于 2025 年 7 月 2 日
- 原文链接: adevarlabs.com/blog/fee-...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 洞察:Layer 1 & Layer2 链 - 2026年1月 47 浏览
- Busha 上的 Solana 支持贷款:尼日利亚加密用户的实用指南 45 浏览
- SVM内部:sBPF JIT安全缺陷和内存泄漏 45 浏览
- Solana的区块构建之战 120 浏览
- 如何使用 Kora 在 Solana 上启用 Gasless 交易 224 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 306 浏览
- 深度解析:Solana 开发者 - 2025 282 浏览
- Gatekeeper 介绍:Helius 边缘网关 444 浏览
- Polymarket交易手册 424 浏览
- Solana 2025 年第四季度更新:度过低迷期 315 浏览
- 质押和链上信贷市场之间的微妙张力 368 浏览
- Solana将击败传统金融 TradFi ,方法如下 343 浏览

