第四卷：CoinJoin匿名性的交叉攻击

螺旋通讯分为五个系列，涵盖了从毛绒玩具到深奥的、深奥的极客内容。不喜欢其中一个？跳过它，老兄。直接滚走就行了。

The Scroll #4：CoinJoin 匿名性的交叉攻击

之所以称为 The Scroll，是有原因的。比特币巫师……大量文字……

由 @not_nothingmuch 撰写

这不仅是我们迄今为止最长的 The Scroll 版本，也可能是我们发布过的最长的文档。但是，你知道吗？这是有充分理由的：如果你想了解比特币隐私，这一点真的、真的非常重要。

以下内容由 Spiral 的比特币巫师 @not_nothingmuch 撰写。与 The Scroll 系列的前一篇文章 一样，这篇文章也伴随着并详细阐述了一个 视频演示。

订阅

以对抗性的思维思考“二十问”

在研究隐私时，将去匿名化视为一种游戏很有用。我们设想一个可以访问某些信息的对手，它试图正确地猜出在一组候选人中，谁对系统中的某个事件负责。为了防止对手获胜，我们需要让它不断猜测，这可能意味着限制其对信息的访问，或者使用随机性来增加其成功所需的信息量。

来源：猜猜是谁？1979 年版……开箱和概述

许多读者会熟悉游戏“猜猜是谁？”。这个游戏可以被描述为两个“ 二十问”游戏的轮流组合。在“二十问”中，你秘密地从给定的集合中选择一个元素，你的对手试图通过问你最多 20 个是非题来正确地猜出它。在“猜猜是谁？”中，双方轮流对战，先猜对的一方获胜。“猜猜是谁？”中的元素集合是固定的，由 24 个卡通人物组成，他们具有各种不同的特征，例如他们的头发颜色或风格。每个角色都有一个唯一的名称，可以明确地识别他们。

是非题的答案可以用一个位来表示：1 或 0。20 个位可以用二进制表示 0 到 1,048,575 范围内的任何整数，即 2²⁰-1。如果一个集合可以被完全排序，则集合中的每个元素都可以通过其在顺序中的编号位置进行索引，从而唯一地标识它。因此，20 位可以唯一地寻址超过一百万个元素中的一个。

虽然 2²⁰ 是可以使用 20 个是非题的答案唯一标识的集合的最大元素数量，但在现实世界中，20 个答案通常包含的信息少于该数量。对于大多数集合和问题组合，事情几乎肯定不会完美地排列，并且并非每个问题都会独立于其他问题来平分候选元素。有些问题的答案可能存在偏差。有些问题的答案可能与其他问题的答案相关。

假设你总是问“你的角色名称是否在 [剩余角色名称的中位数] 之前按字母顺序排列？”而不是问“你的角色是否戴眼镜？”。这是一个 二分查找，它将最大化每个问题的答案的信息量：在每个步骤中，中间名称划分剩余的字符集，并且该问题消除两个一半中的一个。重复地将剩余的候选对象减半将尽可能快地缩小搜索范围，只需要对数数量级的步骤，这比线性扫描（即逐一检查：“是 Alice 吗？不是？Bob 怎么样？……”）快得多。

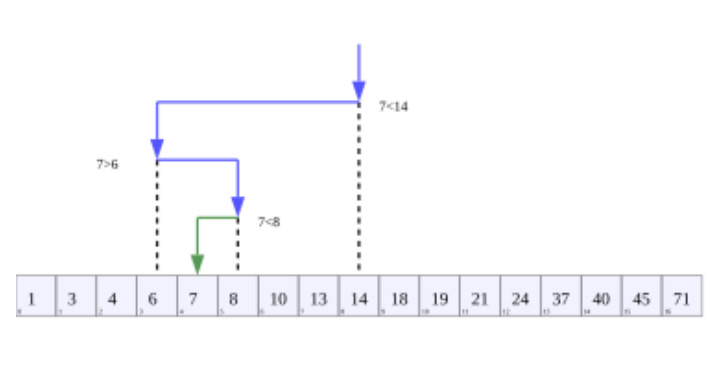来源：二分查找 - 维基百科

请记住，如果你是为了赢得比赛，那么游戏的重点不是从你的对手那里获得最多的信息，而是成为第一个猜对的人，并且事实证明，最大化每个答案的信息实际上 不是最佳策略，至少在诚实地玩游戏时是这样。同样，当使用游戏来研究隐私时，必须假设对手根据其偏好是理性的；很容易意外地为略微不正确的结果进行优化。对手正在努力获胜。

最后，假设不再假设玩家是诚实的。应该很明显，一个人可以undetectably1作弊，而不是在一开始就选择集合的一个元素然后诚实地回答，而是可以始终给出留下最大数量剩余候选者的答案来响应每个问题。因此，自适应选择的答案可以最大限度地降低对手获得有用信息以赢得游戏的速率。在这种所谓的拜占庭环境中，最佳策略不再与玩家诚实时的策略相同。在这里，对手的最佳反应将是坚持二分查找，这限制了自适应游戏的优势。

自适应的“猜猜是谁？”非常无聊，类似于如果你注意的话，井字游戏应该总是以平局结束。准确地说，正如我们将在下一节中看到的那样，有 4.58 位的的信息可以从你的最大对抗对手那里提取出来，并且游戏的规则可以用来迫使对手提交这些位。这意味着第一个玩家总是可以在五个问题后获胜。此类游戏中的答案记录应始终由均匀随机位组成2；任何其他情况都会让对手获得优势。不幸的是，使用这种自适应或添加随机性的隐私保护措施很难构建和理解，因此实际的隐私软件通常比这些玩具示例更难分析。

衡量匿名性

香农熵

“猜猜是谁？”中答案的 信息内容，也称为香农熵，量化了学习它有多么令人惊讶。例如，如果你已经发现对手的角色是秃顶，那么得知他们没有黑发并不会让你感到惊讶，并且此答案不包含任何其他信息。这并不令人惊讶，因为在被告知之前，你可以推断出拥有黑发的概率为零。

假设候选集合中还剩下两个选项；这基本上是掷Coin，两个选项中的任何一个都应该同样可能，因此同样令人惊讶。得知它是选项 A 会告诉你它不是 B，同样，得知它不是 B 会告诉你它一定是 A，因此只需要一个是或否的问题，1 位信息，即可消除所有不确定性。

该值可以从概率分布中计算出来，在本例中，概率分布是 伯努利分布，其中 p=1/2。

首先，计算每个案例概率的以 2 为底的对数的否定式，或者等效地先反转概率并跳过否定式：

−log2⁡(p)=log2⁡(1p)

在这两种情况下

log2(2)=1.

然后，通过将这些值乘以它们对应的概率来缩放这些值，作为一种加权平均值，从而为每种情况贡献 ½ 位。这些项的总和（在本例中为 1）是分布的香农熵。

这也适用于超过两种结果的情况。如果你通过询问“是 [随机角色的名字] 吗？”来开始游戏，那么你很可能只会学习到

124log2⁡(24)≈0.191

如果答案为“否”，则为几位信息。

此时，log₂(23) ≈ 4.52 位量化了你对 23 个同样可能的剩余可能性的剩余不确定性。另一方面，如果你幸运地猜对了，你将学习到完整的 log₂(24) ≈ 4.58 位信息，因为不会有任何不确定性。

只需要不到 5 位即可缩小到 24 个字符中的一个。10 位可以识别 1024 个中的一个。正如我们之前看到的，20 位可以识别大约一百万个中的一个。

香农熵具有足够的通用性，可以量化非均匀分布。并非所有名称都同样流行，因此一个有趣的问题是 一个名称中包含多少熵？链接的帖子估计美国姓氏大约有 15 位。根据 另一篇论文，美国的名字包含大约 10-11 位。这些估计值意味着每个全名最多有 26 位，但请记住，像 John Smith 这样的常见名称包含的信息少于不常见的名称。唯一寻址整个美国人口需要 29 位。

截至撰写本文时，世界人口正在缓慢但肯定地接近 2³³ 人。33 不是一个很大的数字。出生日期中有多少位？仅仅是年龄？某人的 居住城市？IP 地址？最喜欢的电影？浏览器的 canvas 实现？邮政编码？他们词汇中的单词，或他们标点符号的特殊性？这些都是棘手的问题。与这些游戏和现代密码学不同，在这些游戏中，秘密是随机的并且最好是短暂的，我们无法随机化、过期或轮换我们在现实生活中识别属性。

此外，这种个人识别信息通常会在我们的生活中因必要和有时不必要和无意地泄露。我们经常不得不信任与我们互动的人不要透露这些信息，无论是与第三方共享还是意外泄露。也许这与我们必须信任他人的生命没有什么不同，例如医生或专业司机和飞行员。但是，当然，当我们涉及到我们的个人数据时，就信任的必要性而言，这无法相提并论。

熵视角下的匿名性

增强隐私的系统允许用户隐藏在人群中。例如，如果你观察到从 Tor 出口节点到你的服务器的连接，据你所知，可能是数千个 Tor 用户中的一个建立了该连接。非正式地，给定一个去匿名化对手已经观察到的某个事件，也许是通过拦截网络中两个节点之间传输的消息，特定用户的匿名集指的是该事件可能归因于的一组潜在用户。如果匿名消息的接收者被认为是对手，那么他们从一组候选发送者中做出的最佳猜测就是发送者的匿名集。如果这个假设的系统是完全匿名的，那么除了接收者之外，任何用户都同样有可能发送该消息。

两篇有影响力的论文同时发表，提出了用匿名集的熵来衡量匿名性：Claudia Díaz、Stefaan Seys、Joris Claessens 和 Bart Preneel 的 衡量匿名性的方向 和 Andrei Serjantov 和 George Danezis 的 匿名性的信息论度量方向。这些作品从对手无法比偶然更好地从匿名集中猜出正确用户的假设出发，推广到一个考虑了该集合上非均匀概率分布的模型。两者都提出了用熵位来量化匿名集大小。

当匿名集完全对称时，只有均匀分布才有意义，因此将匿名集大小转换为位只是计算 log₂(n) 的问题，其中 n 是集合的大小。例如，集合中 1024 个等概率元素在其分布中具有 10 位的熵。

当分布不均匀时，分布的熵会减少。例如，如果正面或反面都是可能的，但是正面有 ¼ 的概率，反面有 ¾ 的概率，那么该分布的总熵仅为

14log2⁡(4)+34log2⁡(43)=142+340.415...=0.811...

位，而不是完整的位。这可以量化概率分布中表示的不确定性；与公平Coin相比，翻转这枚弯曲Coin的结果相对不确定。

香农熵是整个 熵定义系列 的一个特例。它描述了从可能消息上的概率分布中提取的消息（是或否的答案，或更一般地）中的平均信息内容。更保守的估计可能会使用 最小熵，它只考虑最高概率的元素，而不是计算算术平均值，从而量化最坏的情况。在这篇文章中，我们将坚持使用香农熵。有关熵视角更深入的讨论和更细致的解释，Paul Syverson 的 为什么我不是熵论者 值得一读。

交叉点

在 k-匿名性：一种保护隐私的模型 中，Latanya Sweeney 回顾了她之前的一些结果作为动机，这些结果表明了对“匿名化”数据的重新识别。单独来看，与条目关联的数据集中的每个属性，例如出生日期，可能似乎几乎没有透露该条目的主题。但就像游戏中的是或否问题，只需要对数的信息量，换句话说，令人惊讶的少量属性的组合通常足以进行重新识别：

例如，该研究中的一个发现是，美国 87% 的人口（2.48 亿中的 2.16 亿）具有可能使他们独一无二的报告特征，仅基于 {5 位邮政编码、性别、出生日期}。显然，包含有关这些个人的此类信息的数据发布不应被视为匿名。

粗略估计，5 位数字的字符串将具有 log₂(10⁵) ≈ 16.6 位的最大熵，但邮政编码的数量少于此，log₂(4.3 x 10⁴) ≈ 15.4，并且请记住，人口并非均匀分布在邮政编码中，因此 13.8 将是 更好的估计。在大多数情况下，性别字段通常包含略多于 1 位的信息，因为即使表示非二元性别，大多数条目也将是男性或女性。也就是说，具有非二元值的条目将比该条目的主题揭示更多 1 位的信息。如果没有查看年龄分布，也很难估计出生日期。

忽略 2 月 29 日并假设均匀分布的生日和 2 位数的出生年份，则熵将为 log₂(365 x 10²) ≈ 15.1。同样，可以获得更 现实的估计，即 14.9 位。总而言之，更保守的估计总计约为 29.7 位。为了进行比较，当时美国人口均匀分布的熵为 log₂(248 x 10⁶) ≈ 27.9 位，或 log₂(342 x 10⁶) ≈ 28.4 位，并具有最新的 数据。

该论文中的下图对于任何花时间学习 SQL 中什么是“内连接”的人来说，可能看起来很熟悉。它说明了一个不同的例子，其中 Sweeney 使用相同的字段将医疗记录链接到选民登记列表，从而确定了时任马萨诸塞州州长 William Weld 在“匿名化”医疗数据集中的特定记录：

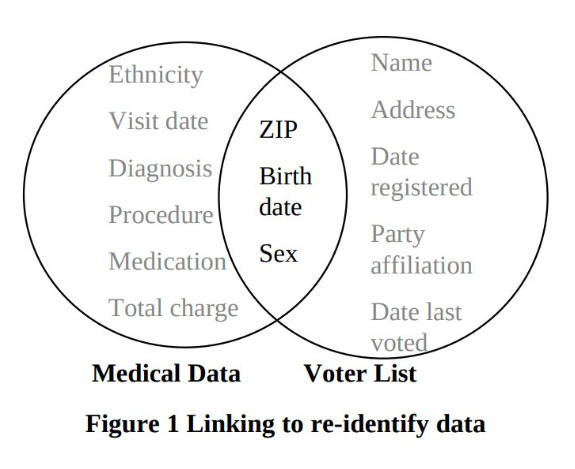来源：k-匿名性：一种保护隐私的模型

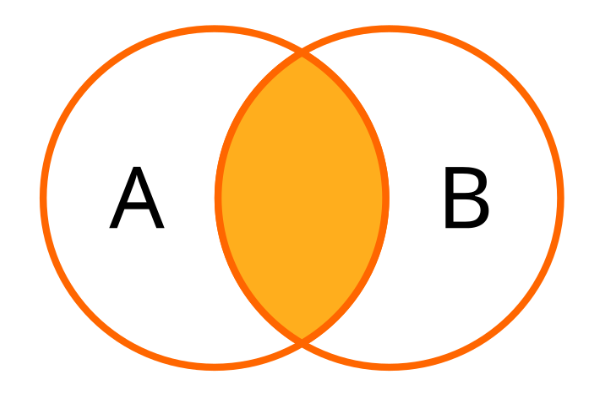来源：文件：SQL Join - 07 A Inner Join B.svg - Wikimedia Commons

这种维恩图，用两个重叠的圆圈表示两个集合，并高亮显示重叠的部分，通常表示两个集合之间的交集。集合是元素的无序集合，例如数据库中的行、数字或任何可以用数学方式定义的东西。两个集合的交集是两个集合中都存在的元素的集合。因此，例如，在选民登记列表中，我们可能会讨论所有邮政编码为 12345 的条目的子集，以及所有出生日期为 1970 年 1 月 1 日的条目的集合。这两个子集的交集是邮政编码为 12345 且 出生日期为 1970 年 1 月 1 日的条目的子集。在州长的情况下，在属性值与他在选民登记列表中的属性匹配的条目的子集中，只有一个条目。

对于具有不同结构的数据集，存在一个小问题：如果我们将它们视为行集合，那么它们的交集将始终为空，因为这些行将具有不同的形状。当计算两个数据库表的内部连接时，只有两个表中都存在的列的值在某种意义上通过指定 JOIN ON a.zip = b.zip AND a.dob = a.dob 或不太可移植的 USING(zip, dob) 语法来交叉，但这些交叉值与它们来自的行相关，因此链接两个数据集的整体结构更复杂。请注意，Sweeney 的图描绘了数据集列的交集，强调了更主要的问题，即“匿名化”数据集中包含的属性无意中与其他公开可用的数据集的属性具有非空的交集。

在 k-匿名性模型的应用方面，该论文中描述的用于匿名化数据集的过程已经不再受欢迎，因为在 Aloni Cohen 的题为 对去识别防御的攻击 的后续工作中发现了一些弱点。k-匿名性的中心思想是确保对于属性的每种可能组合，都至少有 k 行包含数据中的每种特定组合，这表明需要 log₂(k) 的额外信息位才能从其全等条目中识别出一个条目。建议用于确保这种情况发生的去识别程序是以数据相关的方式编辑或概括，例如，从出生日期中删除日期，保留年份和月份，甚至仅保留年份（如果这还不够）。Cohen 的工作表明，低估隐私的脆弱性是多么容易，因为即使丢弃信息直到每种组合都有 k 个，编辑过程本身也会泄漏有关未编辑数据集统计的信息。这种泄露，即使非常微妙，不仅会随着时间的推移而累积，而且通常会复合。使用位来计算隐私损失（这是一个对数刻度）可能有助于更好地理解隐私通常呈指数级衰减的速率。

交叉攻击

在混合网络中，例如 Mixmaster 或最近的 Katzenpost 或 Nym 3，参与者通过一系列中继发送消息，并且每个中继在将消息中继到下一个跃点之前对消息进行洗牌。全局被动攻击者可以观察所有节点接收的所有消息。Onion 加密用于确保混合前后消息不可链接，因此如果至少有一个中继是诚实的，则攻击者无法区分来自洗牌批次的任何单个消息。

然而，随着时间的推移，仍然可以观察到活动模式，事实上，这是不可避免的。混合网络上的统计披露攻击 由 George Danezis 和 Andrei Serjantov 建立在先前的基础上，该基础已经考虑了在尝试将发送者链接到混合网络上的接收者时，可能接收者的集合的交集。该论文中描述的攻击允许攻击者通过交叉攻击目标用户在传输消息的时间间隔内接收消息的所有用户的集合来推断目标用户最有可能与之通信的接收者集合。请注意，在我在这里提出的问题公式中隐藏了一个组合爆炸：输出范围覆盖接收者的所有可能子集，对于 n 个接收者的集合，共有 2ⁿ 个。即使对于几十个用户的 n，这也是一个难以处理的组合数量。这项工作的主要成果是一种有效的近似技术，它使这些类型的交叉攻击更加实用。

CoinJoin 匿名性的交叉攻击

在他们的论文 当 cookie 遇到区块链：通过加密货币进行网络支付的隐私风险 中，Steven Goldfeder、Harry Kalodner、Dillon Reisman 和 Arvind Narayanan 描述了两个独立但相关的攻击。也许更重要的是，他们还通过清楚地展示隐私泄漏如何复合，为更广泛的隐私脆弱性提出了一个令人信服的案例。

在比特币中，coin 的匿名集的一个自然定义是可以 plausibly merged 该 coin 的 wallet clusters 集合（参见 前几篇 文章）。如果候选集群超过一个，则匿名集是非平凡的，在这种情况下，合并将取决于获得额外的信息。新的交易可能会引入不确定性，从而需要为无法合并到任何现有集群的输出创建新的集群（尚未）。另一方面，新的交易和链外信息也可以消除不确定性并促进集群的合并。最常见的是，如果多输入启发式被认为对这种新交易有效，那么输入 coin 的集群将被合并。然而，正如我们之前看到的，存在许多启发式方法，其中一些方法非常准确。

假设 Alice 收到一些比特币到一个由她控制的钱包中。有些可能是从交易所提取的（大概带有 KYC 信息）。也许一个朋友还了她午餐费。也许她卖掉了她的车。在进行了几次交易后，Alice 意识到她的交易历史对所有人可见，并且很容易解释，但很快她将需要进行不是一个，而是两个独立的交易，并且比她迄今为止所依赖的具有更强的隐私保证。

在了解了一些关于隐私的知识后，Alice 决定使用一个支持 CoinJoin 的钱包。通过几次 CoinJoin 交易，她花费了她现有的 coin，获得了显然具有非平凡匿名集的替换 coin。在 CoinJoining 之前，她的钱包可能可以聚集。在 CoinJoining 之后，她现在拥有的每个 UTXO 都无法分配给任何特定集群，因为其他用户的钱包集群也隐含在各种 CoinJoin 交易中。

CoinJoin 隐私背后的直觉是，由于属于不同用户的多个输入用于创建看起来都相同的输出，因此无法将任何一个输出链接到特定的输入。这有点类似于混合网络，其中每个 CoinJoin 交易都是一个中继，而混合的“消息”就是 coin 本身。这种类比非常简单，在实现 CoinJoin 时存在许多导致其崩溃的复杂情况，但我们将在这篇文章中忽略这些细微差别，并相信 Alice 选择的 CoinJoin 钱包，并假设 Alice 始终可以成功地将一个输入花费到每个 CoinJoin 中，并且这会导致她与 CoinJoin 其他参与者的资金的完美混合。在这些假设下，如果 CoinJoin 交易中存在 k 个等效输出，并且输入存在 k 个单独的集群，那么创建此交易时，每个输出的匿名集应具有 log₂(k) 位的熵。

CoinJoin 后聚类

现在为论文中描述的第一次攻击做好了准备。这种攻击之所以成为可能，是因为在商家网站上包含了第三方资源，例如支付处理器的 javascript。假设用于该交易的支付地址透露给第三方，那会将 Alice 的网络会话链接到她的链上交易。该论文发表于 2017 年，因此与网络相关的泄漏的细节现在已经过时了，但此担忧背后的原则与以往一样重要。

Alice 使用她的一个 CoinJoin UTXO 进行第一次需要隐私的交易。假设没有语义泄漏（例如与购买相关的账单地址）或元数据泄漏（也许她 使用 Tor 广播），此交易应保留 Alice 从先前的 CoinJoin 交易中获得的隐私。如此处所绘制的，那将是 1 位的价值。输入或输出的颜色表示已分配给它们的集群。Alice Coin 在红色中，梯度表示模糊性：

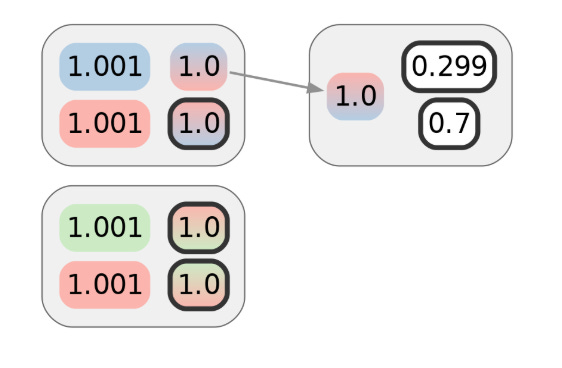
虽然第一笔交易本身并没有透露太多信息，但假设 Alice 进行了另一笔交易。假设它与不同的商家进行交易，但该商家使用的支付处理器与第一个商家相同。天真地看，下图代表了 Alice 支付交易的隐私，并且攻击者需要 2 位的额外信息，每笔交易 1 位，才能将它们都归因于 Alice 的集群：

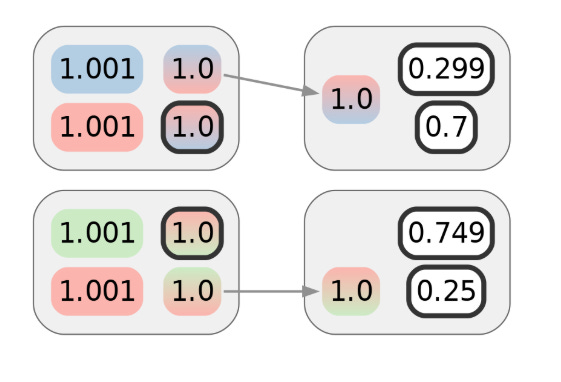
尽管 Alice 希望这与第一笔交易不可链接，但她可能没有意识到她的网络浏览活动正在被跟踪。该论文表明，这种跟踪不仅是可能的，而且甚至在实践上可行，并且可以向第三方透露即使链上显示它们不相关，也可以群集这两笔交易。在视觉上，我们可以用其他颜色表示这种聚类：

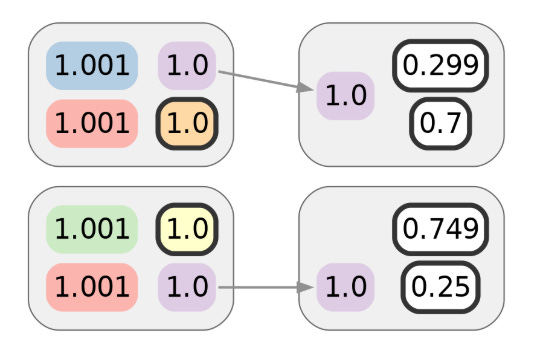
正如论文中所讨论的，网络跟踪只是促进聚类的信息可能泄露的众多方式之一。例如，网站漏洞可能会导致购买记录公开，即使在几年之后也是如此。在至少 一个例子 中，旨在保护受害者的法律诉讼最终通过不适当地揭露有关客户链上交易的信息而使他们受到更多伤害。上一篇关于钱包聚类历史的文章提供了几个额外的例子。

特别是在 CoinJoin 的上下文中，发生这种链接的典型方式是，混合后支付交易的找零输出随后以某种方式进行 CoinJoin，从而导致可以通过对输入进行聚类来链接它们。这也被称为有毒找零问题4，如下图所示。请注意，白色并不代表单个集群，而只是在此示例中缺少聚类信息。

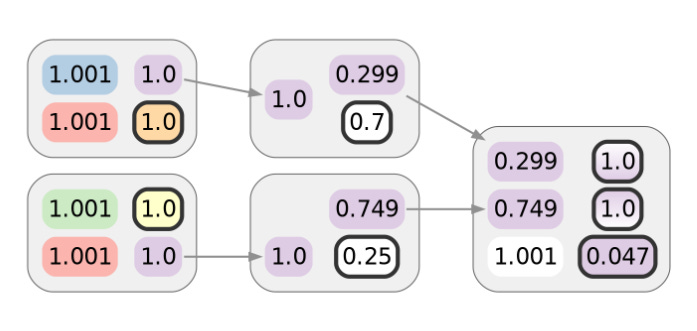
如果所谓的“无需信任”CoinJoin 协议的协调者是恶意的，那么即使 尝试进行 CoinJoin 也可能会链接交易，即使这在链上并不明显。其后果与论文中描述的攻击相同，除了 CoinJoin 协调者还可以假装某些参与者未能及时提交其签名，从而主动但秘密地或至少可以否认地中断回合以获取更多的聚类信息。

交叉前置集群

对 Alice 来说不幸的是，故事并没有就此结束。该论文接下来表明，鉴于这种混合后交易的链接，无论如何得知这种聚类的，对 CoinJoin 交易本身隐私的交叉攻击也成为可能。

就好像攻击者在玩“猜猜是谁？”一样，给定一个支付交易，它试图猜测资金的来源。考虑每个 CoinJoin 交易的输入集。每个花费的 coin 都被分配给某个集群。Alice 参与的每一个 CoinJoin 交易都有一个可链接到 她的 一个集群的输入。此类交易的隐私源于与大量其他无关集群的链接。掌握了混合后交易将多个 CoinJoin 输出链接在一起的知识，攻击者可以计算关联集群集合的交集。一个随机的个人用户参与了 Alice 参与的 每一笔 交易的情况有多常见？那么超过一个用户呢？不太常见。假设交集包含一个唯一的集群，这种情况通常最终会发生。在这种情况下，攻击者将能够将 Alice 的交易相互链接，并将其与 CoinJoin 之前的交易历史链接起来，从而有效地撤销混合。

从视觉上看，这结合了之前图表的推断。对于最后两张图表中紫色集群中的每个 coin，我们可以交叉前一张图表中描绘的梯度中的颜色集合：

{红色，绿色}∩{红色，蓝色}

只有 Alice 的红色集群在交集中，因此可以将紫色集群合并到红色集群中。不仅 Alice 的集群合并了，由于此示例仅有两个用户 CoinJoin 交易，因此其余集群也可以通过消除过程与它们的前代合并，因此在这个特定的例子中，Alice 的可链接支付也可能会对假设的 Bob 和 Carol 进行去匿名化：

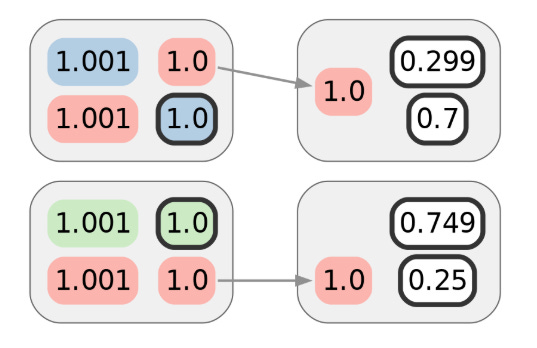
这表明，即使 CoinJoin 的功能像一个完美的混合器（实际上并非如此，但这将在以后的文章中讨论），混合后交易隐私的不足还会破坏之前 CoinJoin 交易的隐私，并且速度比直觉上认为的要快得多。连接比特币交易的图结构包含大量可供去匿名化攻击者使用的信息。

隐私问题通常被轻描淡写，可能是因为在预防甚至控制隐私泄露的挑战面前存在失败主义态度。希望人们的意识能够提高，事情能够像前几十年在密码学领域那样发展，无论是停止使用弱“出口”加密算法 “export” crypto，还是时间侧信道 起初大多被忽视，但现在人们普遍认为它们在实践中可以被利用，并且不考虑它们的实现被认为是不安全的。也就是说，在密码学中，通过优先选择临时密钥而不是长期密钥，或者至少定期轮换长期密钥，我们有更多的机会来限制意外暴露的危害，这始终更具挑战性。可悲的是，在隐私方面，我能想到的最接近轮换密钥的类比是证人保护计划，这是一项相当极端且代价高昂的措施，而且远非完美有效。

在未来的文章中，我们将探讨现实世界中 CoinJoin 隐私面临的一些挑战，以及如何解决第三方的交叉攻击，以及如何处理包含在威胁模型中的不受信任的交易对手。

• 原文链接： spiralbtc.substack.com/p...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～