Schorr 签名基础篇

椭圆曲线密钥体制

在secp256k1上，私钥只是介于0和${2}^{256}$之间的标量整数值。这个数字有多大呢？举个例子，这大概就是宇宙中有多少个原子数量，所以我们有一个巨大沙箱可以玩。

在secp256k1曲线上有一个特殊的点，叫做G，它是“原点”或者“基点”。公钥是通过在曲线上G点自相加k次，来计算出来的ka ，这是标量乘法的定义，写为：
$P=kG$

Schorr 签名

有效的数字签名是提供签名的人知道与消息相关联的公钥对应的私钥，或者他们已经解决了离散对数问题的证据。这一点是数学上保证的， 创建签名的流程通常为：

1 生成一个机密的一次性数字（称为nonce），r。

2 创建公钥R from r（其中$R=r*G$）。

3 将以下内容发送给您的收件人Bob—您的消息（m）、R和公钥（P=k*G）。实际签名是通过对以上所有公开信息的组合进行哈希运算来创建的，以创建一个质询e：
$e=H(R||P||m)$
这里||表示连接，H代表散列函数，使e的范围应该与私钥的范围相同。在我们的例子中，我们需要返回一个256位的数字，所以SHA256是一个不错的选择。现在使用您的私钥构造签名：
$s=r+ke$
s代表签名结果，e值Bob也可以计算，因为m,R,P值Bob均已知，且hash函数Bob也已知

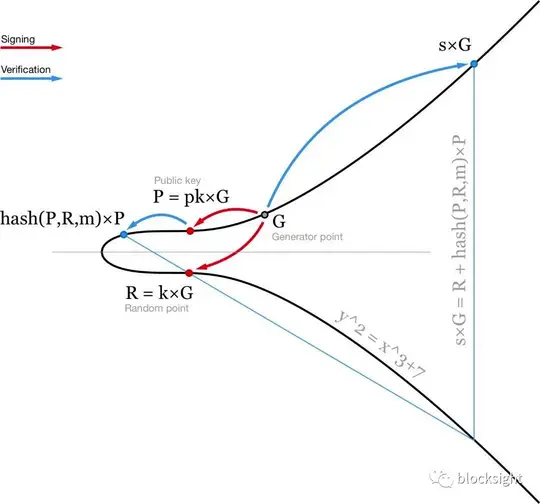
但是他不知道你的私钥k,也不知道nonce r，验证签名过程推理如下:
$sG=(r+ke)G =rG+keG=rG+kGe$
替代$R=rG$,$P=kG$， $sG=R+Pe$, Bob已知R，P，s,e,可计算$sG=R+Pe$验证等式是否成立。

以上过程可用下图表示;

Schnorr 签名中为何要引入随机数r

若不引入随机数r，则直接对消息m做如下签名运算：
$e=H(P||m)$
结果为 $s=ek$我们依然可以验证正确性：$sG=ekG=e(kG)=eP$

看起来好像没什么问题，但是问题出现了:
任何人都能够计算出来私钥数值，$k=s/e$
在加入nonce的情况下，要计算出私钥，必须运算$k=(s-r)/e$ , r是未知的，所以没有切实可行的办法来计算，只要选取的随机数r选取过程中足够随机。

Schnorr签名被认为是随机预言模型中可证明安全的最简单的数字签名方案。它能有效地生成短签名。它被2008年2月到期的美国专利4995082所覆盖。在密码学中，随机oracle是一个oracle（理论上的黑盒），它用从其输出域中统一选择的（真正的）随机响应来响应每个唯一的查询。如果查询重复，则每次提交该查询时，它都以相同的方式响应。

换句话说，随机预言是一个随机选择的数学函数，也就是说，将每个可能的查询映射到其输出域的（固定的）随机响应的函数。