L2 - zkSync证明聚合
- Star Li
- 发布于 2021-05-06 17:25
- 阅读 5565
Matter-Labs开源了PLONK算法的验证电路,能实现多个PLONK证明的聚合证明。聚合电路证明某个证明可验证,并且验证使用的VK是正确的。注意的是,PLONK算法验证的最后一步(配对函数)并没有在电路中验证,而是依赖智能合约进行验证。
PLONK算法虽然只需要一次初始设置,但是证明的计算复杂度相对Groth16算法更高。PLONK算法的好处,远不止初始设置这么简单,因为任何电路都可以共用初始设置,PLONK算法本身的验证逻辑也可以使用初始设置。也就是说,基于PLONK算法可以构建算法验证的电路,从而基于PLONK算法可以证明PLONK算法的证明。
Matter-Labs开源了PLONK算法的验证电路,能证明多个PLONK证明,相关代码链接如下:
https://github.com/matter-labs/recursive_aggregation_circuit
代码量相对比较小,一切从RecursiveAggregationCircuit的synthesize函数开始。
synthesize函数
synthesize的逻辑相对清晰。整个电路实现了如下的功能:
1/ 电路“验证”所有需要证明的proof是否正确
2/ 验证“验证”proof对应的vk是否是指定的那些vk(存储在智能合约)
3/ 打包(packing)所有的公开输入信息(使用sha256算法)
整个逻辑如下图所示,图中的1/2/3就是对应的功能。
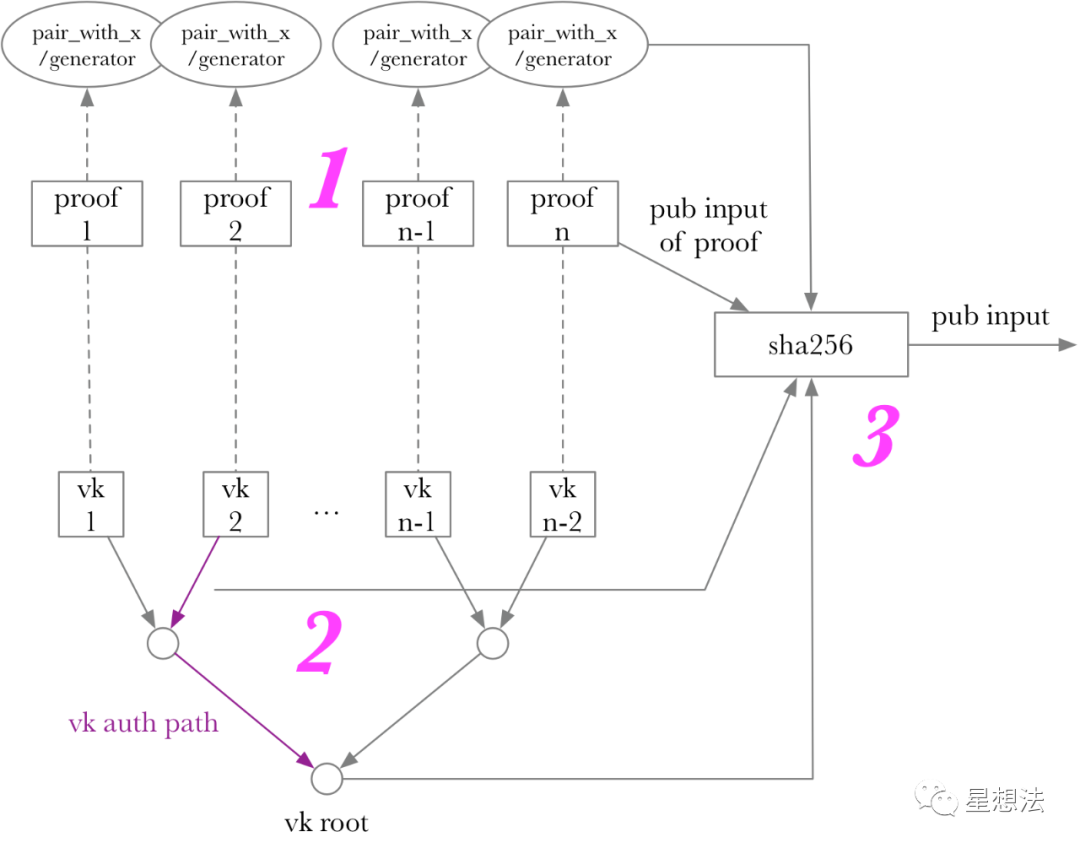
步骤2/3比较简单易懂。核心在步骤1。aggregrate_proof函数实现电路验证某个proof是否正确。
let mut pairs_for_generator = vec![];
let mut pairs_for_x = vec![];
for proof_idx in 0..self.num_proofs_to_check {
let proof = &proof_witnesses[proof_idx];
let vk = &vk_witnesses[proof_idx];
let [pair_with_generator, pair_with_x] = aggregate_proof::<_, _, T, CS::Params, P, _, _>(
cs,
self.transcript_params,
&proof.input_values,
&vk,
&proof,
&self.aux_data,
self.rns_params,
)?;
pairs_for_generator.push(pair_with_generator);
pairs_for_x.push(pair_with_x);
}验证后输出两个结果:pair_with_generator 和 pair_with_x。
查看PlonK算法的验证逻辑的最后可以发现,验证的最后一步是验证两个配对函数:
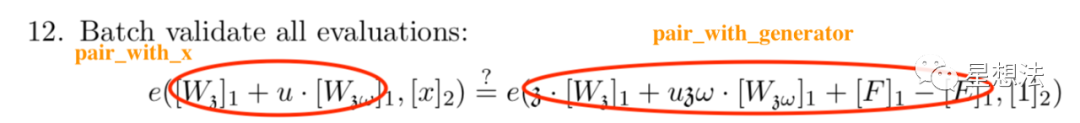
左边的配对函数的g2部分是x,右边的配对函数的g2部分是1(generator)。查看aggregate_proof的函数发现,该“验证”电路,并不验证配对函数的结果是否相等。所以,“验证”电路并没有完整的验证。
aggregate_proof证明了pair_with_generator 和 pair_with_x计算正确。感兴趣的小伙伴可以自行查看该函数。在获得了所有证明的pair_with_generator 和 pair_with_x后,“聚合”在一起。
为了防止攻击,“聚合”采用随机因子:
let mut sponge = StatefulRescueGadget::<E>::new(self.rescue_params);
for w in fs_witnesses.into_iter() {
sponge.absorb_single_value(cs, w, self.rescue_params)?;
}
sponge.pad_if_necessary(self.rescue_params)?;
let aggregation_challenge = sponge
.squeeze_out_single(cs, self.rescue_params)?
.into_allocated_num(cs)?;绑定proof信息生成随机信息。aggregation_challenge就是随机因子,记作c。
let mut scalars = vec![];
scalars.push(aggregation_challenge.clone());
let mut current = aggregation_challenge.clone();
for _ in 1..self.num_proofs_to_check {
let new = current.mul(cs, &aggregation_challenge)?;
scalars.push(new.clone());
current = new;
}每个pair_with_generator/x前面的系数是c^n。在获得相应点对应的系数后,最后做一次multiexp,将多个点“聚合”在一起。
let pair_with_generator = WP::multiexp(
cs,
&scalars,
&pairs_for_generator,
None,
self.rns_params,
&self.aux_data,
)?;
let pair_with_x = WP::multiexp(
cs,
&scalars,
&pairs_for_x,
None,
self.rns_params,
&self.aux_data,
)?;整个过程示意如下:
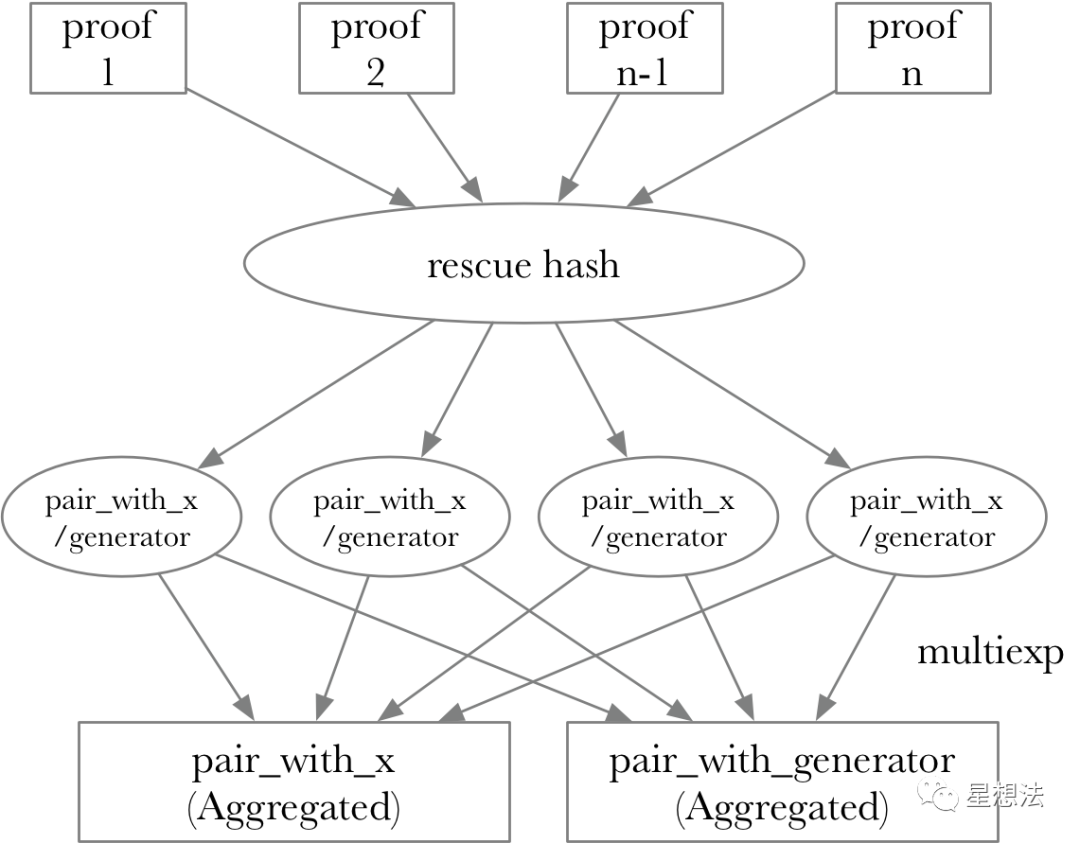
通过这种方法,原本每个proof都需要进行配对函数的验证计算,变成了一次配对函数的验证计算。特别注意的是,配对函数的验证并不是在电路中验证的,这部分的验证在“智能合约”中检查。查看contract/PlonkCore.sol文件的verify_recursive函数:
function verify_recursive(
Proof memory proof,
VerificationKey memory vk,
uint256 recursive_vks_root,
uint8 max_valid_index,
uint8[] memory recursive_vks_indexes,
uint256[] memory individual_vks_inputs,
uint256[16] memory subproofs_limbs
) internal view returns (bool) {
(uint256 recursive_input, PairingsBn254.G1Point[2] memory aggregated_g1s) = reconstruct_recursive_public_input(
recursive_vks_root, max_valid_index, recursive_vks_indexes,
individual_vks_inputs, subproofs_limbs
);
assert(recursive_input == proof.input_values[0]);
(bool valid, PairingsBn254.G1Point[2] memory recursive_proof_part) = aggregate_for_verification(proof, vk);
if (valid == false) {
return false;
}
// aggregated_g1s = inner
// recursive_proof_part = outer
PairingsBn254.G1Point[2] memory combined = combine_inner_and_outer(aggregated_g1s, recursive_proof_part);
valid = PairingsBn254.pairingProd2(combined[0], PairingsBn254.P2(), combined[1], vk.g2_x);
return valid;
}该函数通过aggregate_for_verification函数检查提交的聚合proof本身是否正确。在聚合正确的基础上,调用PairingsBn254.pairingProd2检查“聚合”过的pair_with_x/generator是否正确。
到此,可以看出,这是一种”聚合“证明验证电路,能”部分“验证多个基于PlonK算法的证明。看懂了synthesize函数,再看证明的接口函数就比较容易理解:create_recursive_circuit_vk_and_setup和proof_recursive_aggregate_for_zksync。感兴趣的小伙伴可以自行查看。
电路的核心是电路的验证,PlonK算法的验证都是基于“点”的运算。该电路是如何证明一个椭圆曲线上的点的运算是核心中的核心。
点运算证明
点运算的电路实现在franklin-crypto库的src/plonk/circuit/curve/sw_affine.rs文件中:
pub fn multiexp<CS: ConstraintSystem<E>>(
cs: &mut CS,
scalars: &[Num::<E>],
points: &[Self],
bit_limit: Option<usize>
) -> Result<Self, SynthesisError> {电路证明multiexp采用的是NAF查表法。scalar从高到低的每个bit上点算出来后,double-add。MultiexpTable就是NAF建立的映射表。
有趣的是,在Fq上的点(AffinePoint)的表示:
pub struct AffinePoint<'a, E: Engine, G: CurveAffine> where <G as CurveAffine>::Base: PrimeField {
pub x: FieldElement<'a, E, G::Base>,
pub y: FieldElement<'a, E, G::Base>,
pub value: Option<G>,
}
pub struct FieldElement<'a, E: Engine, F: PrimeField>{
// this is kind-of normal UintX limbs
pub binary_limbs: Vec<Limb<E>>,
// we can not multiply by power of modulus of our base field E,
// so we keep only one single limb
pub base_field_limb: Term<E>,
pub representation_params: &'a RnsParameters<E, F>,
pub value: Option<F>,
}
pub struct Limb<E: Engine> {
pub term: Term<E>,
pub max_value: BigUint,
}为了在Fr上能模拟Fq上的点,Fq上的点分成多个Limb。每个Limb都有单独的变量(Variable)。具体的点的运算以及Multiexp的电路证明,感兴趣的小伙伴可以查看相关代码。
总结:
Matter-Labs开源了PLONK算法的验证电路,能实现多个PLONK证明的聚合证明。聚合电路证明某个证明可验证,并且验证使用的VK是正确的。注意的是,PLONK算法验证的最后一步(配对函数)并没有在电路中验证,而是依赖智能合约进行验证。
<img src="https://img.learnblockchain.cn/pics/image-20210506202627638.png" alt="image-20210506202627638" style="zoom:50%;" />
- 洞察:Layer 1 & Layer2 链 - 2026年1月 65 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 71 浏览
- 来自 Tomasz 的更新 208 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 283 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 398 浏览
- Vitalik: 重新评估以太坊 Layer2 384 浏览
- Layer2战争:为何模块化区块链是2026年Web3的未来 1623 浏览
- 区块链扩容 1855 浏览
- 不同类型的区块链 2546 浏览
- 第十六章. 以太坊扩容 2266 浏览
- Arbitrum Nitro v3.9.0 版本发布 1018 浏览
- 2025年的零知识证明(ZKP):简明完整指南 3107 浏览

