区块链中的数学 -盲签名(Blind Signature)
- blocksight
- 发布于 2021-05-16 14:21
- 阅读 13872
盲签名可以看成结合普通签名的变种,实现特殊的应用。RSA方案简单易解,实际代码工程是要有额外一些处理的,可能需要填充等。
写在前面
上一篇介绍了sigma协议的扩展,我们看到窥探出签名机制的发展一些线索,虽然签名已经介绍了很多常用算法,但还有一些特殊应用场景的签名没有提及,例如盲签名,区块链隐私项目Monero用到的环签名等,不同的是,这些不是独立,自成体系的,而是依赖于之前签名基础,套件等组合变换等实现。
本文重点介绍盲签名机制,虽然目前在区块链中暂时还没看到应用,如果你看到请告诉我!
盲签名(Blind Signature)
盲签名与一般的数字签名不同,一般的数字签名思想是产生一串仅发送者能够产生的别人无法伪造的数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。不同的是,盲签名的签名者是不知道其所签名消息的具体内容,仅在未来某一时刻(以公证人的身份)证明签名的真实性。
具备以下性质:
- 签名者对其签名的消息是不可见的(这就是“盲”的含义),即签名者不知道他所签名消息的具体内容。
- 签名消息不可追踪,即当签名消息被公布后,签名者无法知道这是他何时/哪次的签署的。
注意这里省略了一般签名的性质(不可伪造性和不可抵赖性)。
盲签名流程
一般签名过程的角色只有一个签名者,但是盲签名中不能是同一个角色,因为原始消息必须由另外一个提供者进行盲化处理,称为签名消息的接收者。总体过程:
- 接收者首先将待签数据进行盲变换,把变换后的盲数据发给签名者。
- 经签名者签名后再发给接收者。
- 接收者对签名再作去盲变换,得出的便是签名者对原数据的盲签名。
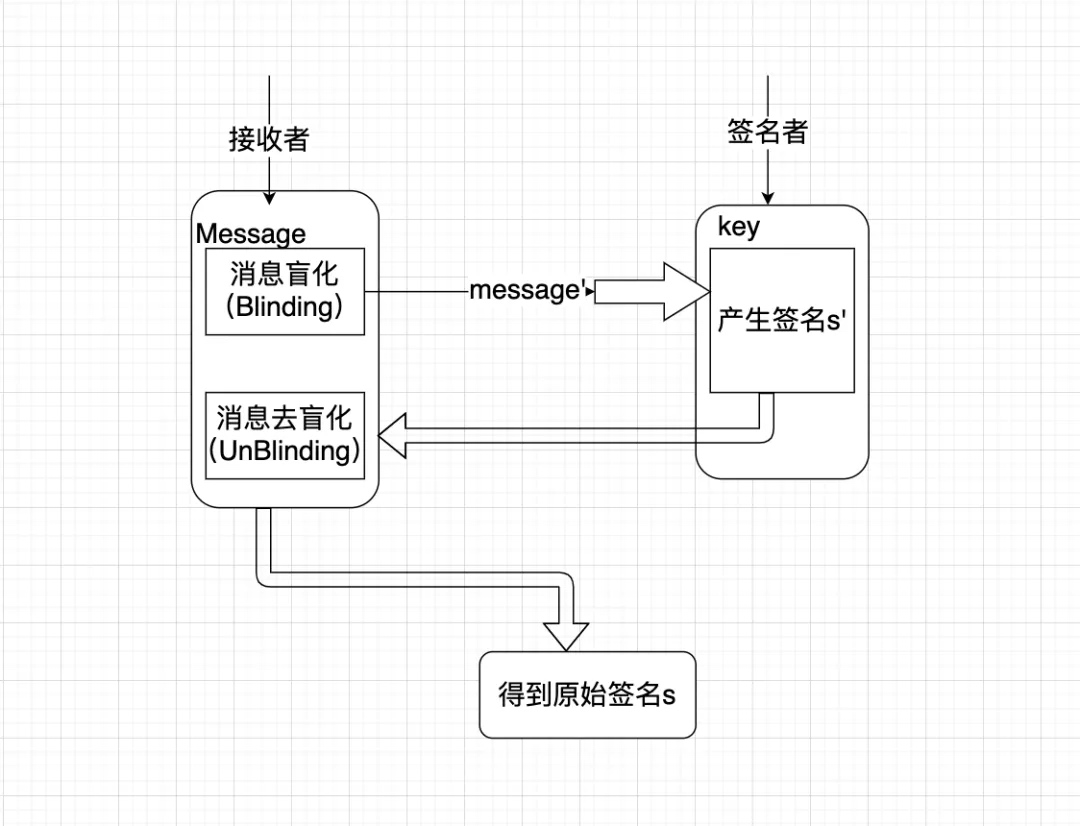
流程上要保证满足盲签名的两条性质,必须使签名者事后看到盲签名时不能与盲数据联系起来。
具体工程实现可以多种,下面介绍与RSA结合的方案!
RSA盲签名原理
假设A是接收者,B是签名者,私钥d, 并公开RSA公钥(n,e), A让B盲签消息m,流程:
- A选取盲因子r,计算$m' = m * r^e\ mod\ n$
- B对m'进行签名$m'^d=(m * r^e)^d\ mod\ n$
- A去盲得到原始签名 $s =m'^d * r^{-1}=m^d\ mod\ n$
易证其正确性,不再赘述(关于RSA详细内容参考历史文章)!
小结
盲签名可以看成结合普通签名的变种,实现特殊的应用。RSA方案简单易解,实际代码工程是要有额外一些处理的,可能需要填充等。
好了,下一节继续介绍Monero项目用到的环签名原理!
原文链接:https://mp.weixin.qq.com/s/gjmWhFVBpVrbW_wCd7UucA 欢迎关注公众号:blocksight
相关阅读
区块链中的数学 - sigma协议OR Proof&签名 sigma协议的扩展--OR proof
区块链中的数学-sigma协议与Fiat-Shamir变换 sigma协议与Fiat-Shamir变换
区块链中的数学 - 何谓零知识证明? 何谓零知识证明
区块链中的数学 - RSA累加器的非成员证明 RSA Accumulator非成员证明以及区块链应用
区块链中的数学 - Accumulator(累加器) 累加器与RSA Accumulator
区块链中的数学 - Kate承诺batch opening Kate承诺批量证明
区块链中的数学 - 多项式承诺 多项式知识和承诺
区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享
区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺
区块链中的数学 - 不经意传输 不经意传输协议
区块链中的数学 - RSA算法加解密过程及原理 RSA加解密算法
区块链中的数学 - BLS门限签名 BLS m of n门限签名
区块链中的数学 - BLS密钥聚合 BLS密钥聚合
Schorr 签名基础篇 Schorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- 以太坊协议研究学习小组 - 2026 启动 250 浏览
- 神奇的 Zig、C 和 OpenSSL 199 浏览
- Shamir份额的魔力:BLS门限签名 469 浏览
- zkMesh:2026年1月回顾 449 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 424 浏览
- ZK 编年史:电路(第二部分) 422 浏览
- 使用 Ecash 票据的谨慎日志合约 368 浏览
- 有限域之美与力量 (以及 Zig) 518 浏览
- 扳手攻击:发生与预防 560 浏览
- zkEVM 安全性概览 638 浏览
- NUT-00:符号、使用方法与术语 421 浏览
- 基于哈希函数的签名(三):多次签名 714 浏览

