剖析DeFi借贷产品之Compound：合约篇
- Keegan小钢
- 更新于 2021-06-15 20:58
- 阅读 9125
理解了Compound合约才能真正理解Compound的业务
前言
概述篇 简单介绍了 DeFi 和借贷的一些现状，以及 Compound 的一些核心概念和产品逻辑，最后介绍了 Compound 的整体架构，其中，智能合约是最核心的模块。
我们都知道，智能合约部署到链上并开源之后，就向全世界公开了自己的代码，如果存在漏洞那可能会酿成灾难性的损失，所以对智能合约的安全性要求非常高。而很多项目都是基于 Compound 做的修改，那么，做技术的人都应该知道，对现有项目的修改，改得越多，越容易引入 BUG，所以，改之前，最好是先熟悉 Compound 的代码实现。而且，熟悉程度越高，改动时，引入 BUG 的概率越低，另外，改动越少，引入 BUG 的概率也越低。要明白，简单就是美。
接下来，就跟随我的脚步来学习 Compound 的那些智能合约吧。
先避坑
当老板对你说：我们准备也搞 DeFi 借贷产品了，你去调研一下借贷龙头产品 Compound 的技术。你会从哪开始着手研究呢？
有些小伙伴就会开始找到 Compound 在 Github 上的开源项目，以下就是它的合约项目地址：
然后就会按照上面的 README.md 文档说明开始进行安装、部署，力求能把项目跑起来。如果真的这么做了，那就已经踩错坑了，一开始研究的方向就错了。我先直接告诉你结论，Compound 的 Github 工程项目是很难跑起来的，不要在工程化这块浪费时间。如果真的要尝试，那时间不要超过一天，即是说，如果一天内不能把工程项目跑起来，那就放弃这条路，迅速转向正确的方向。
正确的方向应该是直接研究它的合约代码。
接着我来解释下为什么。首先，当我们需要基于一个已有项目开发自己的同类产品时，不修改代码是不可能的，那如果不了解代码的话又如何修改？如何才能保证不会改出 BUG ？其次，从产品层面来说，也是需要清楚核心业务的内部逻辑的，存取借还的实现逻辑是怎样的？借款利率和存款利率怎么算的？利息怎么算的？怎么清算的？另外，前端也需要知道存取借还等需要调用哪个合约的哪个函数？展示的数据又要从哪查？等等。这些才是调研一个项目时要核心解决的问题，而要解决这些问题，关键就是要熟悉其代码实现，而且要熟悉到很多细节层面。
工程化的层面，只是为了解决部署问题而已。而部署合约，有很多种方式，不用工程化的框架也可以，用 Remix 也同样可以部署合约。如果你花了大半个月的时间终于把项目跑起来了，接着，老板、产品经理、前端技术开始问你上面的那些问题，你一个都答不上来，那就开始尴尬了。
所以，跳过工程化，直接去研究它的合约代码吧，这才是核心。
梳理合约关系
开始研究一个项目的合约代码时，第一步要做的应该是先梳理清楚合约之间的关系，可以用类图的方式进行整理。以下就是我梳理出来的合约关系图：
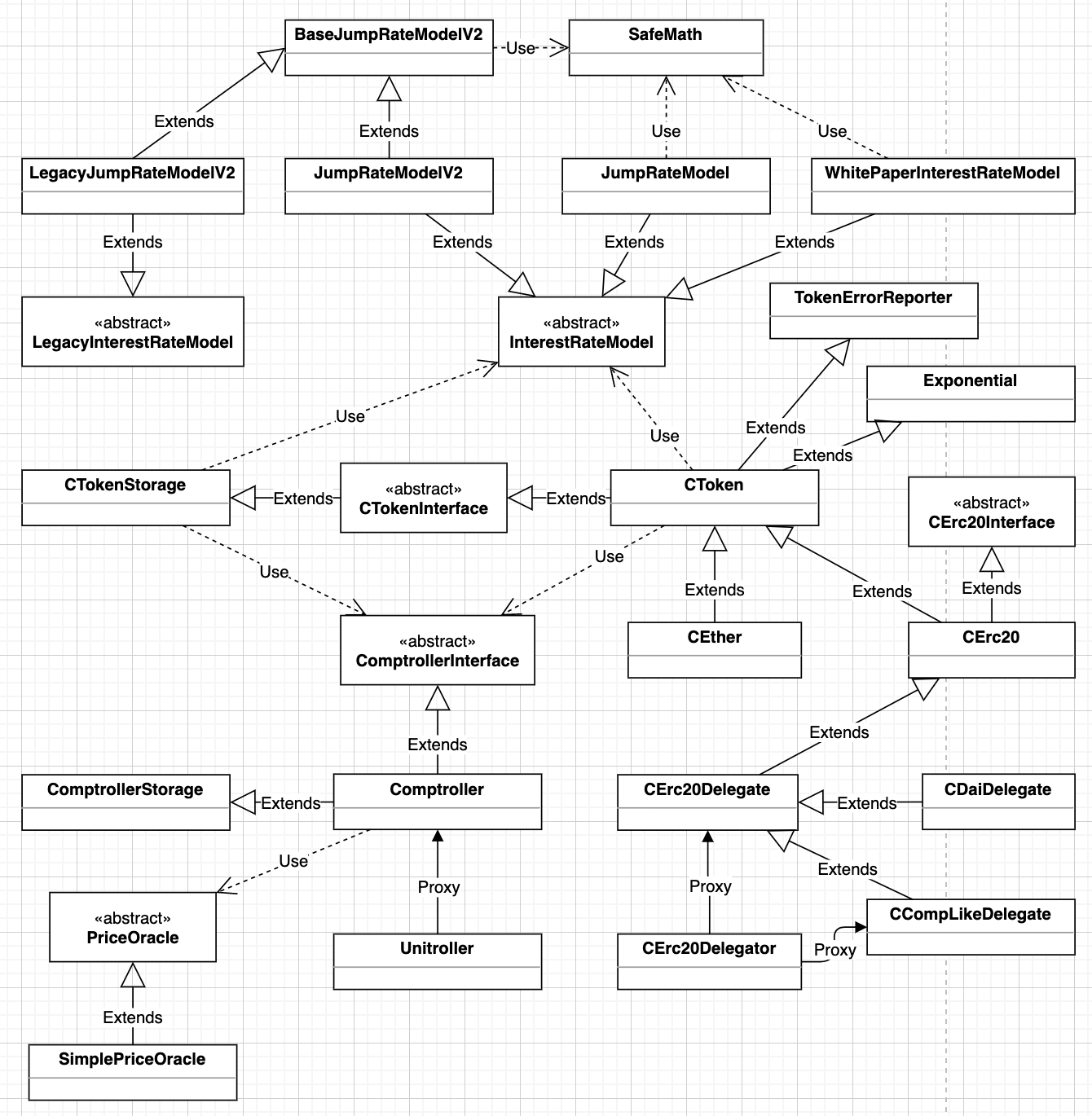
以上的合约关系图中，没包含治理合约。治理属于独立的板块，初期并不需要关心，所以可以先不管。
合约文件虽然有点多，但涉及核心业务的其实可以分为四个模块：
- InterestRateModel：利率模型的抽象合约，JumpRateModelV2、JumpRateModel、WhitePaperInterestRateModel 都是具体的利率模型实现。而 LegacyInterestRateModel 的代码和 InterestRateModel 相比，除了注释有些许不同，并没有其他区别。
- Comptroller：审计合约，封装了全局使用的数据，以及很多业务检验功能。其入口合约为 Unitroller，也是一个代理合约。
- PriceOracle：价格预言机合约，用来获取资产价格的。
- CToken：cToken 代币的核心逻辑实现都在该合约中，属于抽象基类合约，没有构造函数，且定义了 3 个抽象函数。CEther 是 cETH 代币的入口合约，直接继承自 CToken。而 ERC20 的 cToken 入口则是 CErc20Delegator，这是一个代理合约，而实际实现合约为 CErc20Delegate 或 CCompLikeDelegate、CDaiDelegate 等。
下面，对每个模块再分别深入讲解。
InterestRateModel
我们来看看 InterestRateModel 合约的代码：
pragma solidity ^0.5.16;
/**
* @title Compound's InterestRateModel Interface
* @author Compound
*/
contract InterestRateModel {
/// @notice Indicator that this is an InterestRateModel contract (for inspection)
bool public constant isInterestRateModel = true;
function getBorrowRate(uint cash, uint borrows, uint reserves) external view returns (uint);
function getSupplyRate(uint cash, uint borrows, uint reserves, uint reserveFactorMantissa) external view returns (uint);
}其实就是定义了利率模型的接口，但因为声明了一个常量 isInterestRateModel 用来标明这是一个利率模型合约，所以没用 interface 声明，而用 contract，定义成抽象合约。Compound 的很多接口都是采用这种方式定义的。
该接口只定义了两个函数，getBorrowRate() 和 getSupplyRate()，分别用来获取当前的借款利率和存款利率。但这两个利率不是年化率，也不是日利率，而是区块利率，即按每个区块计算的利率。
直线型
而具体的利率模型实现有好几个，WhitePaperInterestRateModel 是最简单的一种实现，也是我前一篇文章所说的直线型的利率模型。所谓的直线，其实是借款利率的，其计算公式为：
y = k*x + by 即 y 轴的值，即借款利率值，x 即 x 轴的值，表示资金使用率，k 为斜率，b 则是 x 为 0 时的起点值。
理解了这条公式之后，我们再来看代码就会很好理解那些值的含义了。先来看看构造函数：
constructor(uint baseRatePerYear, uint multiplierPerYear) public {
baseRatePerBlock = baseRatePerYear.div(blocksPerYear);
multiplierPerBlock = multiplierPerYear.div(blocksPerYear);
emit NewInterestParams(baseRatePerBlock, multiplierPerBlock);
}构造函数有两个入参：
- baseRatePerYear：基准年利率，其实就是公式中的 b 值
- multiplierPerYear：其实就是斜率 k 值
构造函数的实现中，blocksPerYear 是一个常量值，表示一年内的区块数 2102400，是按照每 15 秒出一个区块计算得出的。将两个入参分别除以 blocksPerYear，就分别得到了区块级别的基准利率和区块斜率。
那公式中的 b 值和 k 值都初始化好了，x 值即资金使用率则是动态计算的，计算公式为：
资金使用率 = 总借款 / (资金池余额 + 总借款 - 储备金)
utilizationRate = borrows / (cash + borrows - reserves)其代码实现如下：
function utilizationRate(uint cash, uint borrows, uint reserves) public pure returns (uint) {
// Utilization rate is 0 when there are no borrows
if (borrows == 0) {
return 0;
}
return borrows.mul(1e18).div(cash.add(borrows).sub(reserves));
}其中，mul(1e18) 是为了将结果值扩展为对应的精度整数。
那么，借款利率的实现也很容易理解了，代码如下：
function getBorrowRate(uint cash, uint borrows, uint reserves) public view returns (uint) {
uint ur = utilizationRate(cash, borrows, reserves);
return ur.mul(multiplierPerBlock).div(1e18).add(baseRatePerBlock);
}其中，div(1e18) 则是因为 ur 和 multiplierPerBlock 本身都已经扩为高精度整数了，相乘之后精度变成 36 了，所以再除以 1e18 就可以把精度降回 18。
最后，存款利率又是如何计算的呢？请看代码：
function getSupplyRate(uint cash, uint borrows, uint reserves, uint reserveFactorMantissa) public view returns (uint) {
uint oneMinusReserveFactor = uint(1e18).sub(reserveFactorMantissa);
uint borrowRate = getBorrowRate(cash, borrows, reserves);
uint rateToPool = borrowRate.mul(oneMinusReserveFactor).div(1e18);
return utilizationRate(cash, borrows, reserves).mul(rateToPool).div(1e18);
}整理一下就可得到计算公式为：
存款利率 = 资金使用率 * 借款利率 *（1 - 储备金率）
supplyRate = utilizationRate * borrowRate * (1 - reserveFactor)至此，直线型的利率模型，合约内容就这么多了，还是非常容易理解的。
下面，我们来剖析拐点型的利率模型。
拐点型
拐点型主要有过两个版本的实现，JumpRateModel 和 JumpRateModelV2，目前，曾经使用 JumpRateModel 的都已经升级为 JumpRateModelV2，所以我们就直接研究 JumpRateModelV2 即可。
回想下拐点型的图形，基本特征就是在拐点前的借款利率是一条直线，拐点后则是另一条斜率高得多的直线。
资金使用率没超过拐点值时，利率公式和直线型的一样：
y = k*x + b而超过拐点之后，则利率公式将变成：
y = k2*(x - p) + (k*p + b)其中，k2 表示拐点后的直线的斜率，p 则表示拐点的 x 轴的值。因此，需要初始化的参数有 4 个：b、k、k2、p，分别对应了构造函数中的几个入参：baseRatePerYear、multiplierPerYear、jumpMultiplierPerYear、kink。而几个 PerYear 入参对应的就有几个 PerBlock 变量，和前面一样，就不重复说明了。
那理解了上面的计算公式，我们来看看获取借款利率的代码实现：
function getBorrowRateInternal(uint cash, uint borrows, uint reserves) internal view returns (uint) {
uint util = utilizationRate(cash, borrows, reserves);
if (util <= kink) {
return util.mul(multiplierPerBlock).div(1e18).add(baseRatePerBlock);
} else {
uint normalRate = kink.mul(multiplierPerBlock).div(1e18).add(baseRatePerBlock);
uint excessUtil = util.sub(kink);
return excessUtil.mul(jumpMultiplierPerBlock).div(1e18).add(normalRate);
}
}如果这都还不理解代码实现，请结合公式多看几遍。
而存款利率的计算公式则和直线型的一样，没有变化。因为存款利率是随着借款利率而变的，所以斜率其实也跟随着借款利率而变化。
CToken
CToken 合约管理着 cToken 代币，也管理着借贷的资金池，所以 CToken 的核心地位毋庸置疑。
CToken 合约只是个基类合约，没有构造函数，且还声明了几个抽象函数，由上层合约来实现。上层合约主要分两类，一类是用来处理 ETH 的 CEther 合约，该合约也是用户交互的入口合约；一类是用来处理 ERC20 的 CErc20 合约。在早期版本中，CErc20 也是用户交互的入口合约，但后来做了调整，CErc20 移除了构造函数，改为了初始化函数，增加了 CErc20Delegate 作为其上层合约，而且还增加了 CErc20Delegator 来代理 CToken，作为 cToken 的入口合约。
简而言之，ETH 的 cToken 交互入口是 CEther 合约，仅此一份；而 ERC20 的 cToken 交互入口则是 CErc20Delegator 合约，每种 ERC20 资产都各有一份入口合约。
代理合约很重要，可实现数据与逻辑的分离，是保证 CToken 合约可升级的基础。使用代理合约后，用户对目标合约的所有调用都通过代理合约，代理合约会将调用请求重定向到目标合约中。请看下图：
CErc20Delegator 就对应于图中的 Proxy Contract，而 CErc20Delegate 则对应于 Logic Contract。这种代理模式的基本原理主要是用到了 delegatecall 函数，若想深入理解可实现合约升级的代理模式，可查看此文章：https://blog.openzeppelin.com/proxy-patterns/。
每个 cToken 合约初始化时至少需要指定几个重要参数：
- underlying：标的资产合约，每种 cToken 都对应于每种标的资产
- comptroller：审计合约，所有 cToken 都会使用同一个审计合约
- interestRateModel：利率模型合约，每种 cToken 都有各自的利率模型合约
其中，comptroller 和 interestRateModel 是可以更换的，当两者存在升级版本时，就可以分别调用 _setComptroller(newComptroller) 和 _setInterestRateModel(newInterestRateModel) 更换为升级后的合约。
存取借款等核心业务的入口函数则主要有以下几个：
- mint：存款，之所以叫 mint，是因为该操作会新增 cToken 数量，即 totalSupply 增加了，就等于挖矿了 cToken。该操作会将用户的标的资产转入 cToken 合约中（数据会存储在代理合约中），并根据最新的兑换率将对应的 cToken 代币转到用户钱包地址。
- redeem：赎回存款，即用 cToken 换回标的资产，会根据最新的兑换率计算能换回多少标的资产。
- redeemUnderlying：同样是赎回存款的函数，与上一个函数不同的是，该函数指定的是标的资产的数量，会根据兑换率算出需要扣减多少 cToken。
- borrow：借款，会根据用户的抵押物来计算可借额度，借款成功则将所借资产从资金池中直接转到用户钱包地址。
- repayBorrow：还款，当指定还款金额为 -1 时，则表示全额还款，包括所有利息，否则，则会存在利息没还尽的可能，因为每过一个区块就会产生新的利息。
- repayBorrowBehalf：代还款，即支付人帮借款人还款。
- liquidateBorrow：清算，任何人都可以调用此函数来担任清算人，直接借款人、还款金额和清算的 cToken 资产，清算时，清算人帮借款人代还款，并得到借款人所抵押的等值+清算奖励的 cToken 资产。
以上，每一步操作发生时，都会调用 accrueInterest() 函数计算新的利息。该函数的实现逻辑主要如下：
- 获取当前区块 crrentBlockNumber 和最近一次计算的区块 accrualBlockNumberPrior，如果两个区块相等，表示当前区块已经计算过利息，无需再计算，直接返回。
- 获取保存的 cash（资金池余额）、totalBorrows（总借款）、totalReserves（总储备金）、borrowIndex（借款指数）。
- 调用 interestRateModel.getBorrowRate() 得到借款利率 borrowRate。
- 如果 borrowRate 超过最大的借款利率，则错误退出，否则进入下一步。
- 计算当前区块和 accrualBlockNumberPrior 之间的区块数 blockDelta，该区块数即是还未计算利息的区块区间。
- 根据以下公式计算出新累积的利息和一些新值：
- simpleInterestFactor = borrowRate * blockDelta，区块区间内的单位利息
- interestAccumulated = simpleInterestFactor * totalBorrows，表示总借款在该区块区间内产生的总利息
- totalBorrowsNew = interestAccumulated + totalBorrows，将总利息累加到总借款中
- totalReservesNew = interestAccumulated * reserveFactor + totalReserves，根据储备金率将部分利息累加到储备金中
- borrowIndexNew = simpleInterestFactor * borrowIndex + borrowIndex，累加借款指数
- 更新以下值：
- accrualBlockNumber = currentBlockNumber
- borrowIndex = borrowIndexNew
- totalBorrows = totalBorrowsNew
- totalReserves = totalReservesNew
- 发射 AccrueInterest() 事件。
另外，存取借还时，还会调用 comptroller 对应的 XXXAllowed() 函数进行审计。比如，mint() 函数对应调用 mintAllowed() 函数。
Comptroller
Comptroller 是一个审计合约，顾名思义，主要职责就是对存取借款等核心业务进行审查和校验，查看 ComptrollerInterface 定义了哪些函数就可以看出来，审计函数主要有：
- mintAllowed()：是否允许存款
- redeemAllowed()：是否允许取款
- borrowAllow()：是否允许借款
- repayBorrowAllowed()：是否允许还款
- liquidateBorrowAllowed()：是否允许清算
- seizeAllowed()：是否允许清算抵押物
- transferAllowed()：是否允许转账
另外，对应于以上每个函数，接口中还分别定义了对应的 Verify() 函数，比如 mintVerify()、redeemVerify() 等，但这些 Verify() 函数在 Compound 目前的实现中并没做任何实质性的操作。
借贷市场上要支持哪些资产的存借，也是在 Comptroller 设置的，通过调用 _supportMarket(CToken) 函数进行设置。支持的市场会存储到以下两个数据结构中：
/**
* @notice Official mapping of cTokens -> Market metadata
* @dev Used e.g. to determine if a market is supported
*/
mapping(address => Market) public markets;
/// @notice A list of all markets
CToken[] public allMarkets;用户还可以选择对存入的资产开启或关闭作为抵押品，对应的函数则是：
- enterMarkets(address[] memory cTokens)
- exitMarket(address cTokenAddress)
enterMarkets 可以将指定的多个 cToken 作为抵押品，对应地就可增加用户的可借额度。exitMarket 则可以将指定 cToken 从抵押品列表中移除，但是，如果用户存在借款时，exitMarket 的资产价值不能超过借款价值。用户的抵押品列表会存储在 accountAssets 中：
mapping(address => CToken[]) public accountAssets;其中，address 为每个用户的钱包地址。
而下面这个函数则可以获得用户的资产状况：
/**
* @notice Determine the current account liquidity wrt collateral requirements
* @return (possible error code (semi-opaque),
* account liquidity in excess of collateral requirements,
* account shortfall below collateral requirements)
*/
function getAccountLiquidity(address account) public view returns (uint, uint, uint) {
(Error err, uint liquidity, uint shortfall) = getHypotheticalAccountLiquidityInternal(account, CToken(0), 0, 0);
return (uint(err), liquidity, shortfall);
}其中，返回的 liquidity 表示剩余的可借额度，它是用户的抵押物总价值（乘以抵押因子后的价值）sumCollateral 和总债务 sumBorrowPlusEffects 的差额。当这个差额为正数时，则 liquidity = sumCollateral - sumBorrowPlusEffects，此时 shortfall 为 0；而差额为负数时，则 liquidity 为 0，shortfall = sumBorrowPlusEffects - sumCollateral，此时表示用户债务已经超过了清算门槛，已经可以被清算。
每个市场的抵押因子也是在 Comptroller 中设置的，通过 _setCollateralFactor(CToken cToken, uint newCollateralFactorMantissa) 函数进行设置。
而且，计算用户资产状况时，需要用到价格预言机 PriceOracle，Comptroller 也提供了函数用来设置所使用的价格预言机：
function _setPriceOracle(PriceOracle newOracle) public returns (uint) {
// Check caller is admin
if (msg.sender != admin) {
return fail(Error.UNAUTHORIZED, FailureInfo.SET_PRICE_ORACLE_OWNER_CHECK);
}
// Track the old oracle for the comptroller
PriceOracle oldOracle = oracle;
// Set comptroller's oracle to newOracle
oracle = newOracle;
// Emit NewPriceOracle(oldOracle, newOracle)
emit NewPriceOracle(oldOracle, newOracle);
return uint(Error.NO_ERROR);
}PriceOracle
价格预言机是 DeFi 借贷产品中必不可少的组成部分，前面提到的获取用户资产状态的函数 getAccountLiquidity() 中，计算用户的抵押物价值和债务价值都需要通过价格预言机读取到各种代币的市场价格。
接口层面，PriceOracle 定义了最小化接口，很简单，请看代码：
contract PriceOracle {
bool public constant isPriceOracle = true;
function getUnderlyingPrice(CToken cToken) external view returns (uint);
}就只有一个常量和一个函数，常量 isPriceOracle 只是为了方便检验这是一个 PriceOracle，getUnderlyingPrice() 则会根据 cToken 获取对应的标的资产的价格。
而具体的实现，Compound 使用的是自己的一套价格预言机 Open Price Feed。其机制中有三种角色：Reporter、Poster、View。Reporter 主要是由 CEX、DEX 来承担，主要职责是对一些交易对的币价用自己的私钥进行签名并公开出去，Poster 则负责将 Reporter 已签名的数据发布到链上，View 才是 DApp 实际应用的合约，可以由多个 Reporter 任意组合而成。
Compound 使用的实现类为 UniswapAnchoredView，只使用了一个 Reporter 的签名数据，Coinbase 的价格数据，而任何人都可以充当 Poster 调用该合约的 postPrice() 函数将 Reporter 的价格数据发布到链上。不过有一点需要注意，Coinbase 所签名的价格数据并不是很实时的价格，根据 Compound 官方文档所说的，每隔几分钟才签发一次数据的，所以价格也是滞后几分钟的。postPrices() 函数的声明如下：
function postPrices(bytes[] calldata messages, bytes[] calldata signatures, string[] calldata symbols)UniswapAnchoredView 还提供了一个通用的获取 USD 价格的函数：
function price(string memory symbol) external view returns (uint)最后，自然也实现了 PriceOracle 接口所定义的函数：
function getUnderlyingPrice(address cToken) external view returns (uint)不过，Compound 的这套预言机，因为数据源只有 Coinbase 一家，所以存在被攻击的风险，去年 11 月底就因为攻击者短时操纵了 Coinbase 上 DAI/USD 的价格，使其一度暴涨超 30%，导致 Compound 上的抵押资产大规模被清算。所以，价格预言机的数据源最好是集成多家，采用加权平均法计算得出。
总结
Compound 的合约虽然看起来比较多，但核心业务的其实就那么几个，这几个理解透了，也就搞懂 Compound 的很多业务逻辑细节了。另外，Compound 的很多设计都挺值得学习的，比如它所使用的代理模式，比 OpenZeppelin 所提供的实现简单得多。
不过，也因为限于篇幅原因，很多代码细节无法深入讲解，有兴趣的小伙伴可以私下再找我交流细节问题。
下一篇，我将和大伙聊聊 Subgraph。
扫描以下二维码即可关注公众号（公众号名称：Keegan小钢）
