Paradigm CTF-回文子串
- bixia1994
- 发布于 2021-07-23 19:34
- 阅读 4293
如何更好的节省Gas费用呢?本文提到了5种方法
本题目是Paradigm的CTF系列中挺有意思的一道题,它模仿了leetcode中125. 验证回文串这道题目,通过给定输入,让你判断输入的字符串是不是回文子串,实现用solidity来刷Leetcode,伟大的Samczsun!
目前作者正在找智能合约相关的工作,希望能跟行业内人士多聊聊 🐟 。如果你觉得我写的还不错,可以加我的微信:woodward1993
题目分析
我们先简单看下什么是回文:
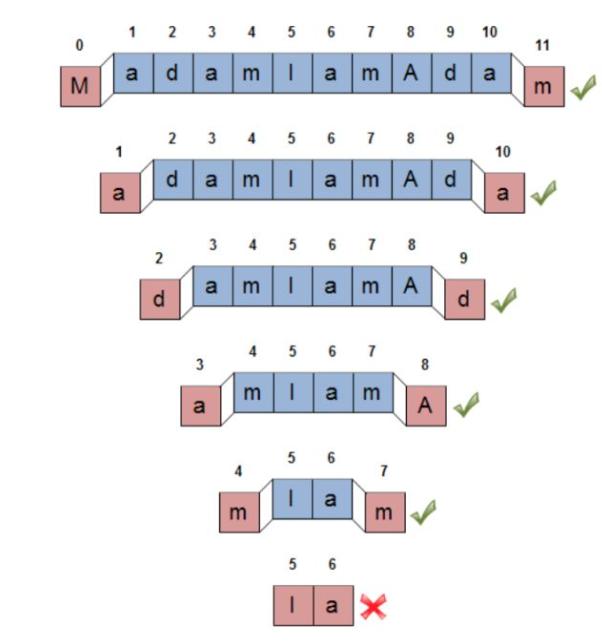
回文就是从左到右读和从右到左读都是一样的字符串成文回文。最经典的解决回文子串的方法是双指针法,如下图所示:
只要left指针和right指针所指的内容不一致,则返回false。直到两个指针相遇,即left < right(这里可以不用取等号,因为奇数时,留下唯一一个肯定是回文)
:one: 定义左右指针
分别定义左指针left,指向字符串左边第一个元素;右指针right指向字符串右边第一个元素
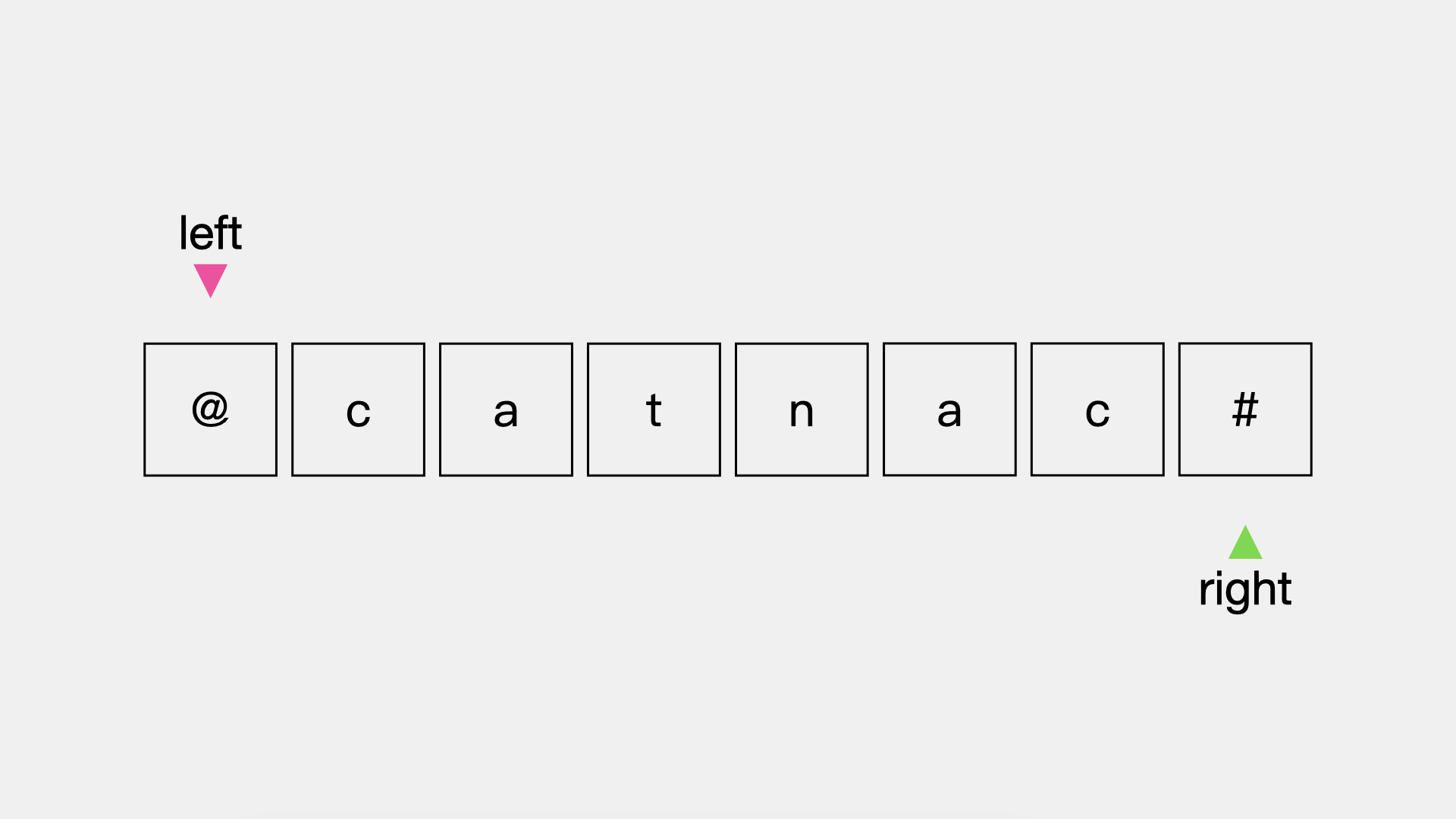
:two:移动指针
这时指针left指向的字符”c“与指针right指向的字符”c“是一样的。left需要向右移动一位。同理,指针right也应向左移动一位。
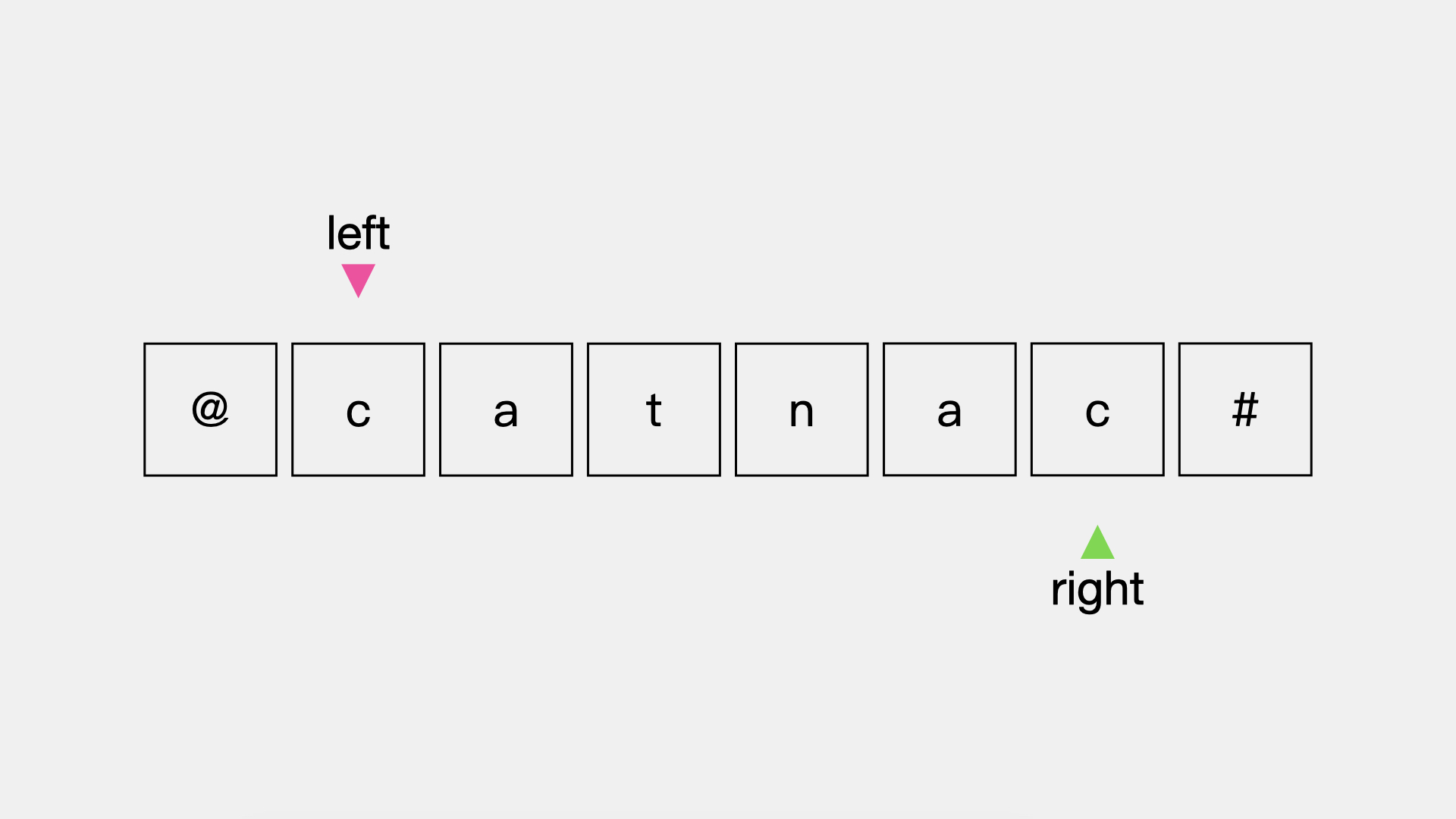
:three:判定退出
指针left指向的字符”t“与right指向的字符”n“是不同的,也就是说字符串"@CaTnAc#"不是回文串。至此,即使有剩余的字符也就不需要考虑了
测试用例:
我们再来看看他的测试用例有哪些:
testcases = {
"": True,
"a": True,
"ab": False,
"aba": True,
"paradigm": False,
"tattarrattat": True,
}思路:
其实该题的难点在于输入参数的判断。:muscle: 真正的判断是否为回文的逻辑是很清晰的。
参数判断 :muscle:
当通过函数test(string)来输入参数如:"aba"时,其aba会被编码为:
0xf9fbd554 => 函数选择器
0000000000000000000000000000000000000000000000000000000000000020 => 动态类型string的编码head
0000000000000000000000000000000000000000000000000000000000000003 => tail[0] 字节长度
6162610000000000000000000000000000000000000000000000000000000000 => tail[1] "aba"的字节数组因为string是一个动态类型,其在编码时,先编码head,在编码tail。head中的内容是tail部分距离该head所占位点的偏移量,是一个相对值。
$$ \mathtt{head}(X_i) = \mathtt{enc}(||head(X1) ... head(X{k-1}) tail(X1) ... tail(X{i-1})||) $$
$$ tail(X_i) = enc(X_i) $$
对于字符串string,其在编码tail时,
- 先转换成字节数组 “aba” => 0x616261
- 得到字节数组的长度 len(0x616261) = 0x03
- 将字节数组左对齐 0x616261 =>0x6162610000000000000000000000000000000000000000000000000000000000
故在结合上head部分,对应的偏移量是0x20, 故test(string)输入参数为aba时的编码如上。
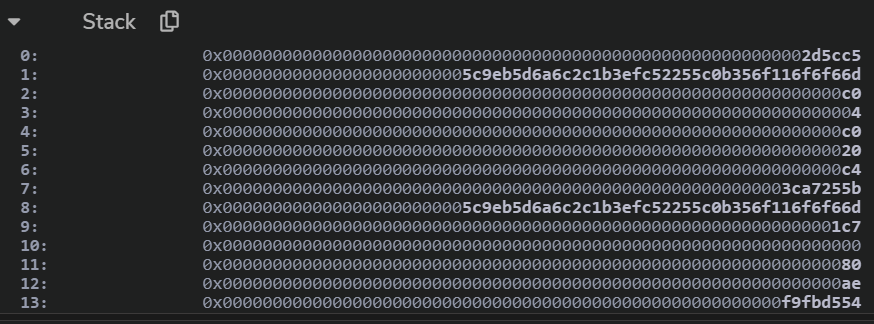
当通过staticcall调用时,其栈情况和内存情况如下:
$\mathtt{gas}=2d5cc5$, $\mathtt{to}=5c9eb5d6a6c2c1b3efc52255c0b356f116f6f66d$, $\mathtt{In offset}=C0$, $\mathtt{Insize}=04$,$\mathtt{Outoffset}=C0$,$\mathtt{OutSize}=20$
那么我理解的calldata应该为:0x3ca7255b
而0x3ca7255b正好是keccak("fwd()")的函数选择器, 故实际上这里的staticcall函数调用的是Challenge合约的fwd()方法。应该返回的是fwd合约的地址:6f16a4f343b671b610476c5dcb740e4c5afcbac1,
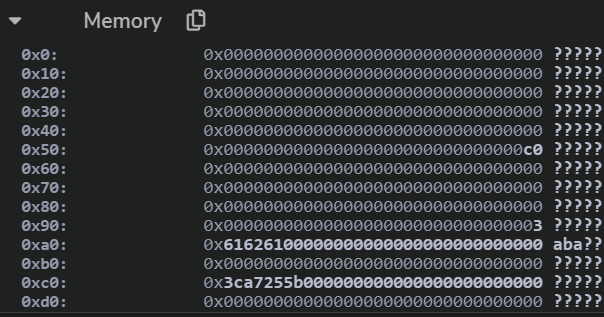
calldata=> 我们发现calldata前面差4位,其是从[04:C4]
xxxxxxxx00000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000000000c0
0000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000003
6162610000000000000000000000000000000000000000000000000000000000
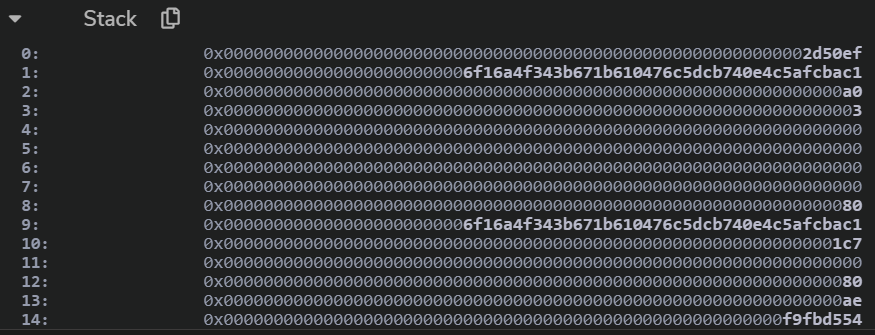
3ca7255b第二次staticcall,此时已经拿到了fwd的合约地址
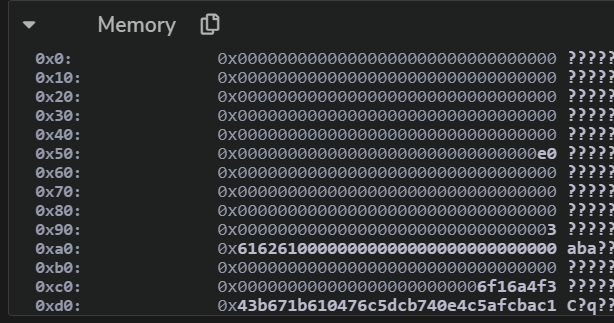
$\mathtt{gas}=2d50ef$, $\mathtt{to}=6f16a4f343b671b610476c5dcb740e4c5afcbac1$, $\mathtt{In offset}=a0$, $\mathtt{Insize}=03$,$\mathtt{Outoffset}=00$,$\mathtt{OutSize}=00$ 此时的calldata是0x616261, 然后就进入了我们自定义的回文逻辑中。
回文逻辑
{
//要比较的字符串在calldata中,其是一个只读的数据结构,需要首先拷贝到内存A中
calldatacopy(0x00, 0x00, calldatasize())
//初始化两个指针,left指向首位A,right指向末位(A+calldatasize()-1)
let left := 0x00
let right := sub(calldatasize(),1)
//比较指针left,right指向的值,如果不等就return false。如果相等,就left++, right--, 直到不满足left < right的条件
//注意mload(left)时,会从left处连续读出32个字节作为left_r的值,但实际上我们只需要头部的一个字节,故需要将其向右侧移动248位。故left_r := shr(248, mload(left))
for {} lt(left, right) {} {
let left_r := shr(248,mload(left))
let right_r := shr(248,mload(right))
if iszero(eq(left_r, right_r)) {
mstore(0x00, 0)
return(0x00, 0x20)
}
left := add(left,0x01)
right := sub(right, 0x01)
}
//最后return true回去
mstore(0x00, 1)
return(0x00, 0x20)
}我们对比下标准答案:
{
let i := returndatasize()
let m := shr(selfbalance(), calldatasize())
let e := sub(calldatasize(), selfbalance())
for {} and(
eq(shr(248, calldataload(i)), shr(248, calldataload(sub(e, i)))),
lt(i, m)
) {i := add(i, selfbalance())} {}
mstore(callvalue(), eq(i, m))
return(callvalue(), 0x20)
}可以发现标准答案有如下特点,其帮助节约大量Gas费用:
- 使用returndatasize()来代替 push1 0x00
- 使用selfbalance()来代替 Push1 0x01
- 使用calldataload(ptr)来代替 mstore(), mload(), 减少一次内存拷贝,直接使用calldataload
- 使用 i == len(calldata)/2 来判定是否成功,如果相等则返回True,如果不等,则返回False。而不是上面写的分别return True和return False
我们根据上述特点,改进一下我们的代码:
{
//要比较的字符串在calldata中,其是一个只读的数据结构,需要首先拷贝到内存A中
//初始化两个指针,left指向首位A,right指向末位(A+calldatasize()-1)
let left := returndatasize()
let right := sub(calldatasize(),selfbalance())
//比较指针left,right指向的值,如果不等就return false。如果相等,就left++, right--, 直到不满足left < right的条件
//注意mload(left)时,会从left处连续读出32个字节作为left_r的值,但实际上我们只需要头部的一个字节,故需要将其向右侧移动248位。故left_r := shr(248, mload(left))
for {} lt(left, right) {} {
let left_r := shr(248,calldataload(left))
let right_r := shr(248,calldataload(right))
// 不匹配,return false 回去
if iszero(eq(left_r, right_r)) {
mstore(0x00, 0)
return(0x00, 0x20)
}
left := add(left,0x01)
right := sub(right, 0x01)
}
//最后return true回去
mstore(0x00, 1)
return(0x00, 0x20)
}节省GAS
利用EVM 的OPCODE来节省Gas消耗的几点建议:
技巧1:用环境变量和区块变量替换常数
这个技巧的应用是为了优化官方解决方案中常量0和1的使用。如上所示,returndatasize()和callvalue()替换了常量0,而selfbalance()替换了常量1。通过这种方法,0和1的使用达到了每次使用1字节的最佳效果。选择returndatasize()和selfbalance()来替换常数的原因是,前者总是0(在任何函数调用之前),而后者通常是我们可以控制的。请记住,平衡表是以wei计算的。其他变量如chainid()或number()也可能被利用,但一般来说用处不大。
技巧2:push一次,dup多次
对于其他经常使用的常量,不能由环境或区块变量来呈现,把它们推到堆栈中(例如,PUSH2 0x9453),然后每当使用它们时,就重复它们(例如,DUP1),以节省(至少)每个额外使用的1个字节。
技巧3:利用特殊操作码的优势
使用强大的操作码,如ADDMOD、MULMOD、BYTE来简化算术操作。例如,为了得到x的第一个字节,使用byte(0, x)而不是shr(248, x)来节省1个字节。如果不需要改变输入的数据,可以考虑用calldataload将其推入堆栈,而不是用calldatacopy推入内存,然后再用mload推入堆栈。
提示4:通过重复使用变量的旧拷贝来避免POP
我们选择在对输入数据进行索引(第三部分)之前将i增加1(第二部分),以避免浪费旧的拷贝。在正常情况下,编译器倾向于在更新一个变量后弹出它的旧拷贝。
0010 DUP1 [i i size]
0011 CALLDATALOAD [data[i] i size]
...
0020 DUP1 [i i size]
0021 SELFBALANCE [1 i i size]
0022 ADD [i+1 i size]
0023 SWAP1 [i i+1 size]
0024 POP [i+1 size]然而,利用旧的dup会让我们节省一个POP和一个DUP。
0010 DUP1 [i i size]
0011 SELFBALANCE [1 i i size]
0012 ADD [i+1 i size]
0013 SWAP1 [i i+1 size]
0014 CALLDATALOAD [data[i] i+1 size]
...提示5:利用执行错误来恢复交易
与明确使用REVERT操作码相比,EVM中的执行错误具有同样的效果,即在不返回任何数据的情况下进行还原。最常见的方式是通过0xfe,也叫INVALID指令,它只有1个字节长。如果你想根据一个特定的条件进行还原,可以使用JUMPI跳到一个不是JUMPDEST的偏移量进行还原。
pc instruction stack
---- -------------- ----------------------------------
0000 CALLDATASIZE size
0001 RETURNDATASIZE size 0
0002 JUMPDEST
0003 DUP1 size i i
0004 SELFBALANCE size i i 1
0005 ADD size i i+1
0006 SWAP1 size i+1 i
0007 CALLDATALOAD size i+1 data[i]
0008 DUP2 size i+1 data[i] i+1
0009 DUP4 size i+1 data[i] i+1 size
000A SUB size i+1 data[i] size-i-1
000B CALLDATALOAD size i+1 data[i] data[size-i-1]
000C XOR size i+1 xor
000D RETURNDATASIZE size i+1 xor 0
000E BYTE size i+1 byte
000F RETURNDATASIZE size i+1 byte 0
0010 JUMPI size i+1 // revert 如果byte != 0,则revert
0011 DUP2 size i+1 size
0012 DUP2 size i+1 size i+1
0013 LT size i+1 cont
0014 PUSH1 0x02 size i+1 cont 0x02
0016 JUMPI size i+1 //
0017 STOP size i+1最后:
pragma solidity 0.8.0;
import "./Setup.sol";
contract Exploit {
constructor(Setup setup) payable {
setup.challenge().deploy(hex"3660006000376000600136035b80821015604357815160f81c815160f81c8082141515603057600060005260206000f35b60018401935060018303925050505b600c565b600160005260206000f35050");
payable(setup.challenge().fwd()).transfer(1);
payable(setup.challenge().rev()).transfer(1);
}
}
- # Kyber Exploit 数学取整分析 902 浏览
- paradigm ctf 2022 - Hint finance 4330 浏览
- Sudoswap是如何节省gas的 5149 浏览
- HACK Reply XCarnival 4690 浏览
- gymdefi hack 5565 浏览
- APE 空投 5008 浏览
- Paraluni Hack Reply 4756 浏览
- ERC721A 算法分析与设计 9053 浏览
- MasterChef 2 6180 浏览
- masterChef learning 6243 浏览
- Compound简化版v2 4955 浏览
- Simplified Compound Protocol Design 4513 浏览

