Vitalik：受信任初始化的原理是什么?

来源 | vitalik.ca

作者 | Vitalik Buterin

翻译 | 双花 (@doublespending)

校对 | ECN

编者注：

数据可用性采样 (data availability sampling) 是 Dankshading 的关键部分，为实现这一密码协议，需要使用 KZG 仪式对数据可用性证明方案所需要的参数进行初始化。

因此，KZG 受信任初始化是实现 EIP-4844 (proto-danksharding) 和完整版 Danksharding 的重要前提条件。

除此之外，其他密码学协议如 ZK-SNARKs 领域也需要有受信任初始化阶段。

本文介绍了受信任初始化的运作原理以及其验证过程。

推荐阅读：

《Vitalik: Proto-Danksharding FAQ》

《大幅简化的新分片设计》

《分片 + 数据可用性采样》

必要的背景知识：elliptic curves and elliptic curve pairings。另请参阅：Dankrad Feist's article on KZG polynomial commitments。(中文版：KZG多项式承诺)

特别感谢 Justin Drake、Dankrad Feist 和 Chih Cheng Liang 的反馈和评审。

许多密码协议尤其是在数据可用性采样和 ZK-SNARKs 领域都依赖于受信任初始化。受信任初始化仪式是一个用于生成一批数据的一次性流程。后续，每次运行某些密码协议时都必须使用这些数据。生成这些数据需要一些秘密信息； “信任”来源于这样一个事实，即必须由某个人或某组人来生成这些秘密，使用秘密来生成数据，然后发布数据并销毁这些秘密。然而，一旦生成了数据并销毁了秘密，仪式创建者就不需要进一步的参与。

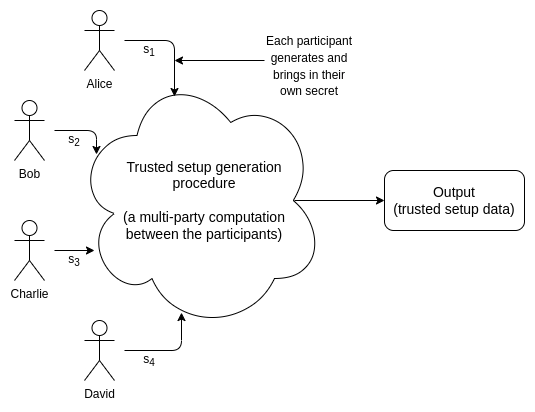
受信任初始化有很多类型。在主流协议中最早使用的受信任初始化的实例是 2016 年的 Zcash 启动仪式。这个仪式非常复杂，而且需要多轮的通信交互，因此只能有六名参与者。彼时彼刻，每个使用 Zcash 的人都必须相信六名参与者内至少有一名是诚实的。新式协议一般会使用 powers-of-tau 初始化技术，其遵循 1-of-N 信任模型，N 值通常为数百。也就是说，数百人一起参与生成数据，只需其中一人是诚实的并且不公开秘密就能保证最终输出的安全性。实践上，像这样的执行良好的受信任初始化通常被认为是“足够接近于去信任”的。

本文将介绍 KZG 初始化如何运作及其工作原理，以及受信任初始化协议的未来。任何精通代码的人都可以随意地浏览以下代码实现：https://github.com/ethereum/research/blob/master/trusted_setup/trusted_setup.py.

Powers-of-tau 初始化是怎样的？

powers-of-tao初始化由两系列的椭圆曲线点组成，如下所示：

[$G{1}$, $G{1}s$,$G_{1}s^{2}$...$G{1}*s^{n{1} -1} ]$

[$G{2}$,$G{2}s$ , $G_{2}s^2$...$G{2} *s^{n{2}−1}$]

$G{1}$ 和 $G{2}$是两个椭圆曲线群的标准生成元；在 BLS12-381 中，$G{1}$占用 48 字节（压缩形式）， $G{2}$占用 96 字节。$n{1}$, $n{2}$分别是初始化输出的$G{1}$, $G{2}$生成点列的长度。一些协议要求 $n{2}=2$，另一些协议要求 $n{1}$和 $n{2}$的值都较大，一些协议属于中间情形（例如，当前的以太坊数据可用性采样方案要求 $n{1}=4096$ 和 $n_{2}=16$）。$s$ 是用于生成点列的秘密值，使用后需要销毁。

为了对多项式 $P(x)= {\textstyle \sum{i}c{i}x^{i} }$生成 KZG 承诺，我们简单选取一个线性组合$ {\textstyle \sum{i}c{i}S{i} }$ ，其中 $S{i}=G{1} *s^{i}$（受信任初始化中的椭圆曲线点列）。初始化中的 $G{2}$用于验证我们所承诺的多项式的值；我不会在此讨论验证流程的细节，更多的细节参见 Dankrad 的文章。

直观地说，受信任初始化提供了什么价值？

从更深层次理解这里面到底发生了什么，以及受信任初始化为何能够提供这些价值。多项式承诺使用大小为 $O \left ( 1 \right )$的对象（单个椭圆曲线点）对一段大小为 $N$ 的数据进行承诺。我们可以用简单的 Pedersen 承诺来做到这一点：只需将 $S{i}$的值设置为 $N$ 个不相关的随机椭圆曲线点，然后如前所述对 ${\textstyle \sum{i}^{}} c{i}S{i}$多项式进行承诺。实际上，这正是 IPA 证明所做的。

然而，任何基于 IPA 的证明都需要 $O\left ( N \right )$ 时间来验证，有一个不可避免的原因：使用基点 $\left [ S{0},S{1}...S{i} ...S{n-1} \right ]$ 对多项式 $P\left ( x \right )$ 生成的承诺会对应于使用基点 $ \left [ S{0},S{1}...\left (S{i}*2\right ) ...S{n-1}\right ]$ 的另外一个多项式。

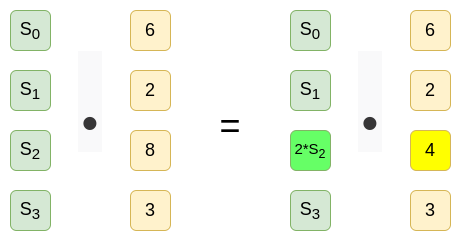
在一组基点下对多项式 $$3x^{3} +8x^{2} +2x+6$$ 的一个有效承诺等效于另一组基点下对多项式 $$3x^3+4x^2+2x+6$$ 的一个有效承诺。

如果我们想对某些命题生成基于 IPA 的证明（例如，该多项式在 $x=10$ 时等于$3826$），该证明在基于第一组基点时应当验证通过，而在基于第二组基点时应当验证失败。因此，无论验证流程如何，都无法避免以某种方式考虑每一个 $S_{i}$值，因此不可避免地需要 $O\left ( N \right )$ 时间。

然而，如果有受信任初始化的话，点间存在着隐藏的数学关系。可以保证任意两个相邻点之间有着相同的因子 $s$ 使得 $S{i+1}=s*S$。如果 $\left [ S{0},S{1}...S{i}...S{n-1} \right ]$ 是有效的初始化输出，“被篡改的输出” $\left [ S{0},S{1}...\left (S{i}*2 \right ) ...S_{n-1} \right ]$是无效的。因此，我们不需要 $O\left ( N \right )$ 的计算量；相反，我们利用这个数学关系就可以在 $O\left (1\right)$时间下验证我们需要验证的任何东西。

然而，数学关系必须保密：如果 $s$ 已知，那么任何人都可以提出一个表示众多不同多项式的承诺：如果 $C$是$ P(x)$ 的承诺，那么它也是 $\frac{P\left ( x \right )*x }{s} $或 $P\left ( x \right ) -x+s$或许多其他多项式的承诺。这将完全破坏所有多项式承诺应用的根基。因此，虽然在某个时间点上必须存在一些秘密值 $s$，让 $S_{i}$值之间的数学联系成为可能，从而实现高效验证，但是 $s$ 也必须被销毁。

多方受信任初始化如何运作？

单个参与者进行初始化是很简单的：只需选择一个随机值 $s$，并使用 $s$ 值生成一系列椭圆曲线点。但单个参与者的受信任初始化是不安全的：你必须信任某个特定的人！

解决方案是多方受信任初始化，其中“多”指的是很多参与者：超过 100 人是正常的，对于较小计算量的初始化方案，可能会超过 1000 人。以下是多方 powers-of-tau 初始化的工作原理。

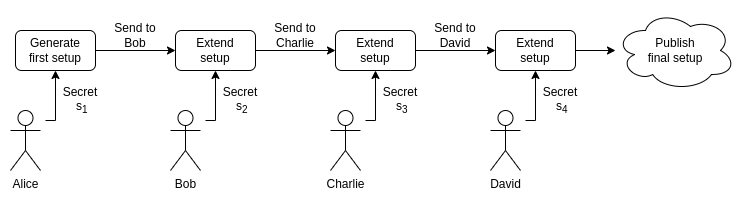
以一个已有的初始化输出为切入点（注意，你不知道s的值，你只知道一系列的椭圆曲线点） $\left [ G{1},G{1}s,G_{1}s^{2}...G{1}*s^{n{1}-1} \right ]$ $ \left [ G{2},G{2}s,G_{2}s^{2}...G{2}*s^{n{2}-1} \right ]$

现在，选择你自己的随机秘密值 tt。计算：$ \left [ G{1},\left ( G{1}s \right ) t,\left ( G{1}s^{2} \right )t^{2}...\left ( G{1}s^{n_{1}-1} \right )t^{n{2}-1} \right ]$ $\left [ G{2},\left ( G{2}s \right ) t,\left ( G{2}s^{2} \right )t^{2}...\left ( G{2}*s^{n{2}-1} \right )*t^{n_{2}-1} \right ]$

请注意，这相当于：

$\left [ G{1},G{1}\left ( st \right ) ,G{1}\left ( st^{2} \right ) ...G{1} \left ( st^{n{1}-1} \right ) \right ]$ $\left [ G{2},G_{2}\left ( st \right ) ,G{2}*\left ( st^{2} \right ) ...G{2} *\left ( st^{n_{2}-1} \right ) \right ]$ 也就是说，您已经创建了一个秘密值 $s∗t$ 相对应的有效初始化输出！你永远不会把你的秘密值 $t$ 给到之前的参与者，同时之前的参与者也不会把他们的秘密值 $s$ 给到你。只要任意一个参与者是诚实的，并且没有透露他那部分的秘密值，那么组合起来的秘密值就不会被泄露。特别地，有限域具有这样的性质：如果你知道 $s$ 但不知道 $t$，并且 $t$ 是被安全随机地生成的，那么你对 $s∗t$ 的值一无所知！

验证受信任初始化

为了验证每个参与者确实参与了受信任初始化，每个参与者都可以提供这样一个证明，包括 (i) 他们收到的点 $G{i}∗s$ 和 (ii) $G{2}∗t$，其中 $t$ 是他们引入的秘密值。这一系列的证明可用于验证最后的初始化输出将所有的秘密值组合起来 (与之相反的是，最后一个参与者只是舍弃了前面的值，并输出了仅由他自己秘密值生成的初始化结果，他可以自行保留这个秘密值，从而在任何使用该初始化输出的协议中欺诈)。

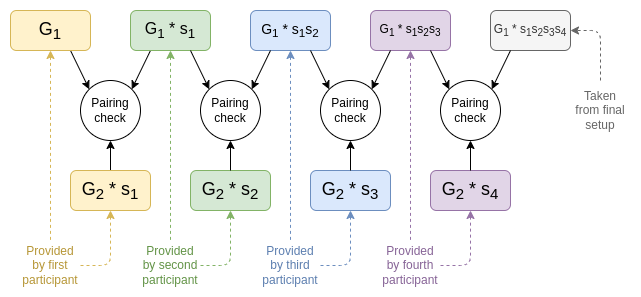
$$s{1}$$ 是第一个参与者的秘密值，$$s{2}$$ 是第二个参与者的秘密值，以此类推。在每个步骤中的配对检查验证了每个步骤的初始化输出确实源自前一步骤初始化输出以及参与者在当前步骤中已知的新秘密值的组合。

（译者注：配对的特性 $e(G{1}*s{1}, G{2}*s{2}) = e(G{1}*s{1}s{2}, G{2})$）

每个参与者都应该在一些公开可验证的媒体（例如个人网站、来自其 eth 地址的交易、推特）上披露他们的证据。请注意，这个机制并不能阻止某些人声称参与了某个阶段，而实际上是另外的人（假设其他人已经透露了他们的证据），但通常会认为这不成问题：如果有人愿意就参与的情况撒谎，他们也会愿意就秘密的删除情况撒谎。只要公开声称参与的人中至少有一人是诚实的，那么初始化就是安全的。

除了上述检查以外，我们还想验证初始化中的所有椭圆曲线点的幂次都是正确的（即，它们是相同秘密值的幂）。（译者注，即椭圆曲线可以表示为序列 $Gs^{i-1}$ ）为此，我们可以进行一系列配对校验，验证 $e\left ( S{i+1},G{2} \right ) =e\left ( S{i},T{1} \right )$（其中 $T{1}$ 是初始化中 $G{2}s$ 的值）。这验证了每个 $S{1}$ 和 $S{i+1}$之间的因子与 $T{1}$T和 $G{2}$之间的因子相同。然后，我们可以在 $G{2}$侧执行相同的操作。（译者注，即验证 $e(T{i+1}, G{1})=e (T{i}, S{1})$ )（其中 $S{1}$是初始化中 $G_{1}s$的值）

然而，这需要很多次配对，成本很高。相反，我们采用随机线性组合 $L{1}= {\textstyle \sum{i=0}^{n{1}-2}} r{i}S{i}$ ，及相同线性组合移动一位的结果：$L{2}= {\textstyle \sum{i=0}^{n{1}-2}} r{i}S{i+1}$ 。我们使用单个配对校验来验证它们是否匹配得上：$e(L{2}，G{2})=e(L{1}，T{1})$

我们甚至可以将 $G{1}$侧和 $G{2}$侧的校验过程结合在一起：除了如上所述计算 $L{1}$ 和 $L{2}$ ，我们还计算 $L{3}= {\textstyle \sum{i=0}^{n{2}-2}} q{i}T{i}$ ($q{i}$是另一组随机系数）和 $L{4}= {\textstyle \sum{i=0}^{n{2}-2}} q{i}T_{i+1}$，然后验证 $e\left ( L2，L3\right)=e \left ( L1，L4\right)$。

拉格朗日形式的受信任初始化

在许多用例中，你不太愿意使用系数形式的多项式（例如 $P\left( x \right)=3x^{3}+8x^{2}+2x+6$，你更愿意使用点值形式的多项式（例如 $P(x)$ 是在域 $[1,189,336,148]$ 模 337 的值为 $\left [19,146,9,187 \right ]$ 的多项式）。（译者注：此处的逻辑是，n 次多项式需要 n+1 个点来进行确定，点值形式其实指的是$P(1)=19,P(189)=146$，如此类推）点值形式有很多优点（例如，您可以在 $O(N)$ 时间内进行多项式的乘法，某些情况下的除法运算），你甚至可以把它用在 $O(N)$ 时间内求值。特别地，数据可用性采样要求 blobs 使用点值形式进行表示。

为了处理这些情况，通常可以便捷地将受信任初始化转换为点值形式。这让你能得到点值（上面的例子中为 $[19,146,9,187]$），并直接使用它们来计算承诺值。

使用快速傅里叶变换（FFT）是最为便捷的手段，但是要将曲线点而非数值作为输入进行传递。我将避免在此重复对FFT进行详细的解释，但这里有一个实现；FFT 实际上并不难。

受信任初始化的未来

Powers-of-tau 并不是唯一的受信任初始化方案。其他一些（实际上或潜在）值得注意的受信任初始化方案包括：

• 旧版的 ZK-SNARK 协议中使用的更为复杂的初始化方案（例如，参见此处)有时仍会被使用（特别地，Groth16)，因为它验证成本会比 PLONK 更低。

• 一些密码协议（例如，DARK) 依赖于隐阶群，群中元素不知道进行多少次乘法运算才能得到零元素。目前存在着完全无信任的版本（请参阅：class groups)，但目前为止，最高效的版本使用的是 RSA 群（$x $的幂 mod $n=pq$，其中 $p$，$q$未知）。遵循 1-of-n 信任假设的受信任初始化方案是 可能的，但实现起来非常复杂。

• 如果/当 不可区分混淆变得可行时，许多依赖于它的协议将会涉及：某人创建和发布一个混淆程序，该程序使用内部的隐藏秘密来执行某些操作。这就是受信任初始化流程：创建者需要持有秘密值来创建程序，而且之后需要把秘密值删除。

密码学仍然是一个快速发展的领域，受信任初始化的重要性很容易会改变。采用 IPA 和 Halo 式思想的技术方案可能会被改进到让 KZG 变得过时和不必要的程度，或者在十年后量子计算机让基于椭圆曲线的所有方案都变得不可行，届时我们将不得不使用无需受信任初始化基于哈希的协议。KZG 改良得更快，或者出现一个依赖于另一种受信任初始化的全新密码学领域都是有可能的。

在一定程度上，受信任初始化是必要的，重要的是要记住，并非所有受信任初始化都水平相当。176 个参与者比 6 个更好，2000 个更佳。相比于要求运行一个复杂软件包，成本小得可以在浏览器或手机应用上进行的受信任初始化仪式（例如，ZKopru 初始化就是基于Web应用）能够吸引多得多的参与者。理想情况下，每个仪式都应当让参与者运行多个独立构建的软件实现，并且运行在不同的操作系统和环境之上，以减少共模故障的风险。参与者只需一轮交互的仪式（如powers-of-tau）远远优于多轮交互的仪式，这既是因为能够支持更多参与者，也是因为编写多个实现会更加简单。理想情况下，仪式应该是通用的（一个仪式的输出能够支持大量协议）。这些都是我们可以并应当继续钻研的事情，以保证受信任初始化尽可能的安全可靠。

特别感谢 ECN 社区翻译志愿者 @doublespending 对本文的翻译贡献。

ECN的翻译工作旨在为中国以太坊社区传递优质资讯和学习资源，文章版权归原作者所有，转载须注明原文出处以及ethereum.cn，若需长期转载，请联系eth@ecn.co进行授权。

本文首发于：https://www.ethereum.cn/Technology/how-do-trusted-setups-work