密码学：后量子密码学中的模数是多少？
- ChinaDeFi 去中心化金融社区
- 更新于 2022-11-16 15:47
- 阅读 1669
公钥加密的旧篇章即将结束，新篇章即将开启。在20世纪70年代末完成的工作对我们很有帮助，但现在我们面临着量子计算机会打破这些方法的威胁。
只要是从事网络安全或安全软件开发的人，就都可能已经了解过公钥加密以及在20世纪70年代末和80年代前后创建的方法。现在我们可能需要学习更多的理论，因为我们所学的方法可能会受到量子计算机的威胁。
如果想开始学习这些新方法，那就有必要往下读了。
(mod p) 运算
在传统的公钥加密中，我们使用一个模数来创建有限域。虽然这听起来很复杂，但实际上这是一个非常简单的概念。对于有限域，我们引入一个模数，它通常是一个素数。对于素数，我们从整数除法中确定余数，然后取余数作为结果。例如，如果素数为17，我们将得到 0 到 16 范围内的输出值：
5 (mod 17) = 6 19 (mod 17) = 2 100 (mod 17) = 15
(mod p)运算的伟大之处在于，我们仍然可以进行加减乘除，并最终得到相同的结果，例如：
15 (mod 17) +100 (mod 17) = (15+100) (mod 17) = 13 15 (mod 17) 100 (mod 17) = (15100) (mod 17) = 4
在离散对数中，我们经常使用Diffie Hellman方法，我们选择一个共享素数 (p) 和一个共享生成器值 (g)，并计算：
A = g^x (mod p) B = g^y (mod p)
交换A和B，共享密钥为：
K = A^y (mod p)
之所以有效，是因为：
K = A^y (mod p) = (g^x)^y (mod p) = g^{xy} (mod p)
在RSA方法中，我们使用模数(N)。对于加密，我们有：
C = M^e (mod N)
要破译：
M = C^d (mod N)
在这种情况下，N是两个素数的乘积，RSA 的优势在于分解模数 (N) 的难度。椭圆曲线方法也使用一个素数(p)的模数，其中我们有：
y² =x³ + ax + b (mod p)
这将我们在椭圆曲线上使用的点的值限制在 0 和 (p-1) 之间。
多项式
但是，量子计算机将破解RSA、椭圆曲线和离散对数，那么后量子密码学中的模数相当于什么？我们可以使用格加密，这涉及到我们使用多项式值来表示我们的位串。
如果我们有一个值19，它可以表示为10011和一个多项式值：
x⁴+x+1
67可以用1000011表示，并且是一个多项式：
x ⁶+ x +1
如果我们把这两个多项式相加，我们得到：
( x⁴ + x +1)+( x ⁶+ x +1)= x ⁶+ x ⁴+1+1
因为我们使用的是 Base 2，所以 1+1 等于 0，因此我们得到：
( x⁴ + x +1)+( x ⁶+ x +1)= x ⁶+ x ⁴
同样的道理也适用于添加相同的幂，例如:
x⁴ + x⁴ = 0 x⁴ + x⁴ + x⁴ = x⁴
以此类推。
在格密码中，我们用多项式进行加，减，乘，除。一个运算可能有一个x³+x+1的多项式，和一个x²+1的秘密多项式，然后将它们相乘得到一个结果。为了恢复原来的值，我们可以除以秘密多项式。
但是，我们如何将多项式的最大幂限制在有限域内呢？就像我们用传统的公钥方法那样，我们用一个模数，然后除以模数，保留余数。
有限域的模数
有限域或Galois域(GF)具有有限数量的元素，并且阶数等于素数 (GF(p)) 或素数的幂 (GF(2^ p ))。例如，GF(2^n)有2^n个元素，它的元素被称为二元多项式(其中多项式因子的系数要么为零，要么为一个值)。为了将多项式减少到给定的大小，我们使用一个模数多项式，它除以输出值。对于GF(128)，我们可以使用x ⁷+ x +1 的模数。
让我们举个例子：
a = x³ + x ²+1
b = x ⁶+ x ⁴+ x ³+1
当我们相加时，得到：
a + b = x ³+ x ²+1+ x ⁶+ x ⁴+ x ³+1= x ⁶+ x ⁴+ x ²
现在，我们把它们相乘：
a × b =( x ³+ x ²+1)×( x ⁶+ x ⁴+ x ³+1)= x⁹ + x ⁷ + x ⁶+ x ³+ x ⁸+ x ⁶+ x ⁵+ x ²+ x ⁶+ x ⁴+ x ³+1= x ⁹+ x ⁸+ x ⁷ + x ⁵+ x ⁴+ x²+1
我们现在用这个值除以模数。在此例中，对于 GF(128)，模数是x⁷ + x +1：
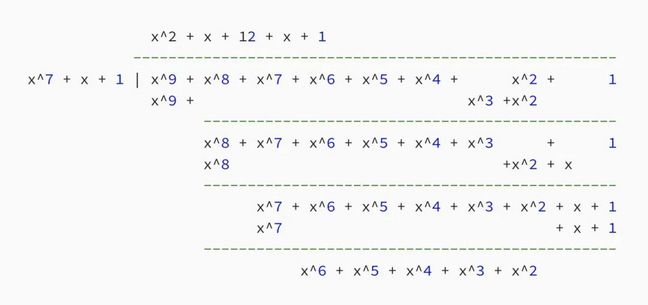
对于GF(128)， a×b的结果如下：
a × b = x ⁶+ x ⁵+ x ⁴+ x ³+ x ²
在Sage中：
示例运行：
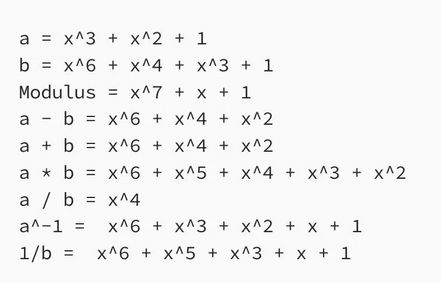
如果我们现在使用 GF(256) ：
示例运行：
我们可以看到，在Sage中GF(256)的默认模数为：
x ⁸+ x ⁴+ x ³+ x ²+1
我们可以在 Sage 中使用列出默认模值：
给出了：
不可约多项式
就像公钥加密中的素数一样，我们需要一个不能被任何数整除的多项式。为此，我们使用一个不可约多项式。不可约多项式的例子有：
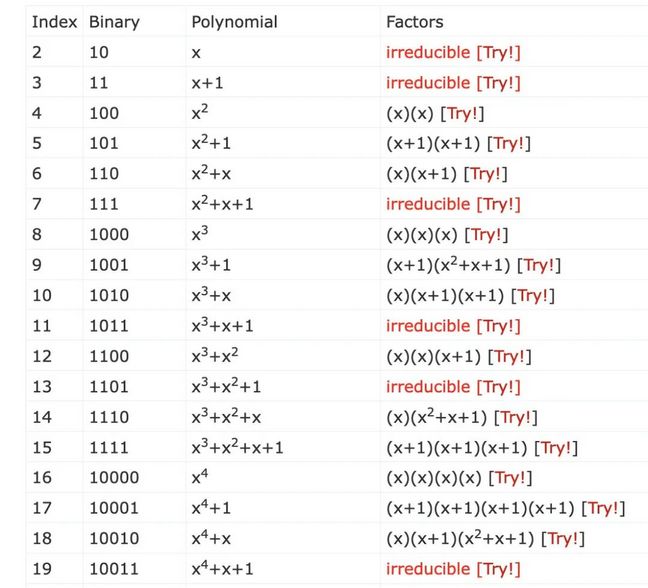我们的不可约多项式是x、x²、x²+x+1 和 x³+x²+1。它们等价于我们在传统公钥加密方法中使用的素数，并类似于(mod p)运算。一种常用的方法是 x⁸+x⁴+x³+x+1，用于AES加密。在Sage中，我们可以定义自己的模数，例如：
k.<x>= GF(2^8, modulus=x^8+x^4+x^3+x+1)<x>= GF(2^8, modulus=x^8+x^4+x^3+x+1)如果我们有y = x ⁵+ x ³+ x ²+1 的输入值 101101，我们乘以h = x ⁴+ x +1，我们得到：
r = yh = (x⁵+x³+x²+1) × (x⁴+x+1)然后我们可以创建以下Sage代码：
\# Rijndael finite field
k.<x>= GF(2^8, modulus=x^8+x^4+x^3+x+1)
y = (x^5+x^3+x^2+1)
h= (x^4+x+1)
r=y*h
print(f"(x^5+x^3+x^2+1) * (x^4+x+1)= {r} ({r.integer_representation()})")当运行时，我们会得到的结果：
$ sage 1.sage
(x^5+x^3+x^2+1) * (x^4+x+1)= x^7 + x^4 + 1 (145)现在可以除以我们的不可约多项式，得到原来的值：
\# Rijndael finite field
k.<x>= GF(2^8, modulus=x^8+x^4+x^3+x+1)
y = (x^5+x^3+x^2+1)
h= (x^4+x+1)
r=y*h
r2=r/h
print(f"{r}/ (x^4+x+1)= {r2} ({r2.integer_representation()})")
得到的结果：
$ sage 1.sage
x^7 + x^4 + 1/ (x^4+x+1)= x^5 + x^3 + x^2 + 1 (45)
我们可以看到乘法，除法，加减法，这些运算都是可逆的。
结论
公钥加密的旧篇章即将结束，新篇章即将开启。在20世纪70年代末完成的工作对我们很有帮助，但现在我们面临着量子计算机会打破这些方法的威胁。事实上，我们开发的方法从来都不是真正可证明的难题——它们只是在传统计算机中难以破解。所以，让我们来看看多项式，模和格的奇妙世界。
关于
ChinaDeFi - ChinaDeFi.com 是一个研究驱动的DeFi创新组织，同时我们也是区块链开发团队。每天从全球超过500个优质信息源的近900篇内容中，寻找思考更具深度、梳理更为系统的内容，以最快的速度同步到中国市场提供决策辅助材料。
