区块链中的数学 -- 蒙哥马利模乘

写在前面

在模运算计算中，蒙哥马利模乘（通常称为蒙哥马利乘法）是一种执行快速模乘的方法。它是由美国数学家彼得·蒙哥马利于1985年提出的. 有过实际工程经验的同学都知道，当整数规模达到一定程度（比如大于200为，$2^{200}$ ）,传统取熵求模运算会非常慢，瓶颈在于昂贵的除法运算。这也是蒙哥马利模乘出现的历史背景，凡事必有因！

蒙哥马利模乘算法关键是依赖于一种称为蒙哥马里形式(Montgomery form)的数字的特殊表示。效率高主要是因为避免了昂贵的除法运算。蒙哥马利形式采用一个常数R>N（N是要模的数），该常数与N互素，蒙哥马利乘法中唯一需要的除法是除以R。可以选择常数R，实际上R总是选2的次方，因为2的次方的除法可以通过位移位实现。这样除以R就容易了，大大提高了算法的速度。

相关概念

设N表示正整数模。商环$Z/NZ$由模N的剩余类组成，也就是说，它的元素是形式为 $a+kN,k \in Z$ 其中a的范围跨越整数。每个剩余类都是一组整数，因此该集合中任何两个整数的差都可以被N整除。对应于a的剩余类表示为a。剩余类的相等称为同余，并表示为

$a=b\ mon\ N$

在计算机上存储整个剩余类是不可能的，因为剩余类有无限多的元素。相反，同余数作为代表进行存储。通常，这些代表是整数a，其中$a \in [0,N-1]$. 如果a是一个整数，则a的表示形式写为a mod N。在写同余时，通常用它表示的余数类来标识一个整数。根据此约定，上述等式写为 a ≡ b mod N。例如  N = 17，5 = 22 mod 17, 22在模17运算下的剩余类代表是5.

Note: 前面提到了商环，之前的文章详细介绍了群的性质。环是带有两种运算的代数结构， 比群要满足更多的性质。商环简单理解是将已有环划分成几个不相交的集合， 类似于商群的性质。详细内容可自行学习。

接下来说下蒙哥马利模乘算法的核心：蒙哥马利形式(Montgomery form)

Montgomery form 蒙哥马利形式

选取一个与N互素的整数R， 如果 a 和 b 是范围 [0, N-1] 内的整数, 蒙哥马利形式表示如下： a' = a R mod N b' = b R mod N

假设 N = 17，R = 100。数值 3、5、7 和 15 的蒙哥马利形式分别是 3' = 3 * 100 mod 17 = 11，5' = 5 * 100 mod 17 = 7，7' = 7*100 mod 17 = 3，和 15' =  15 * 100 mod 17 = 4。 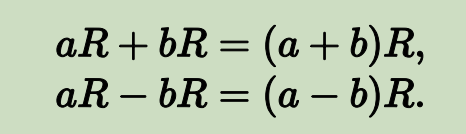蒙哥马利形式中的加法和减法与普通模加法和模减法相同，这是由于分配律的原因：因为 gcd(R, N) = 1，乘以 R 是在加法群 $Z/NZ$ 上的同构映射。例如，(7 + 15) mod 17 = 5，这在蒙哥马利形式中变为 (3 + 4) mod 17 = 7。加减法相对简单，在蒙哥马利形式下进行乘除法更复杂。普通的 aR 和 bR 的乘积不表示 a 和 b 的乘积，因为它多了一个因子 R。

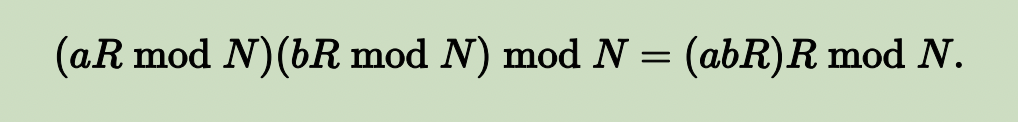
在蒙哥马利形式中计算乘积需要去除额外的因子 R。虽然除以 R 是便宜的，但中间乘积 (aR mod N)(bR mod N) 并不可被 R 整除，因为模运算已破坏了这个性质。因此，例如，在模 17 中，使用 R = 100，7 和 15 的蒙哥马利形式的乘积是 3 和 4 的乘积，即 12。由于 12 不能被 100 整除，需要额外的工作来去除额外的因子 R。去除额外的因子 R 可以通过乘以一个整数R的逆 R' 来实现，使得 RR' ≡ 1 (mod N)，也就是说，R' 的剩余类是 R 对模 N 的模反元素。然后，在模 N 下进行运算。

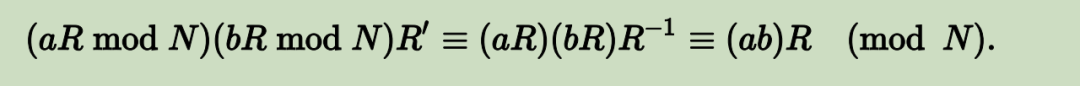
整数 R' 的存在是基于 R 和 N 互质的假设。有办法计算出R'（参照之前系列文章）。这表明可以在蒙哥马利形式下进行乘法运算。因此，一种直接的算法是将 aR mod N、bR mod N 和 R' 视为整数相乘，并对模 N 进行约简。例如，a =3, b= 4,要在模 17 中以蒙哥马利形式相乘 ≈ 和 15，同样使用 R = 100，计算 3 和 4 的乘积得到 12，可以预先算 R' = 8。将 12 乘以 8 得到 96，并对模 17 进行约简得到 11。这正是预期的数值 3 的蒙哥马利形式。\ (a * b)R * R' mod N = (ab)R' mod N   = 3 * 4 * 8 mod 17 = 11 = 3'（3的Montgomery form）

REDC algorithm

尽管上述算法是正确的，但由于需要乘以 R' 并除以 N，它比标准表示中的乘法运算慢。蒙哥马利约简，也称为REDC算法，是一种同时通过 R' 计算乘积并更快地对模 N 进行约简的算法，比起朴素方法更加高效。与传统的模约简专注于使数值小于 N 不同，蒙哥马利约简专注于使数值更容易被 R 整除。它通过添加一个选择的小倍数的 N 来实现，该倍数被选择为抵消模 R 的余数。将结果除以 R 得到一个更小的数。这个数值比较小，几乎等于模 N 的约简值，而计算模 N 的约简只需要最后的条件性减法。因为所有的计算都只使用 R 而不是 N 进行约简和除法，所以该算法比通过除法进行朴素模约简更快。

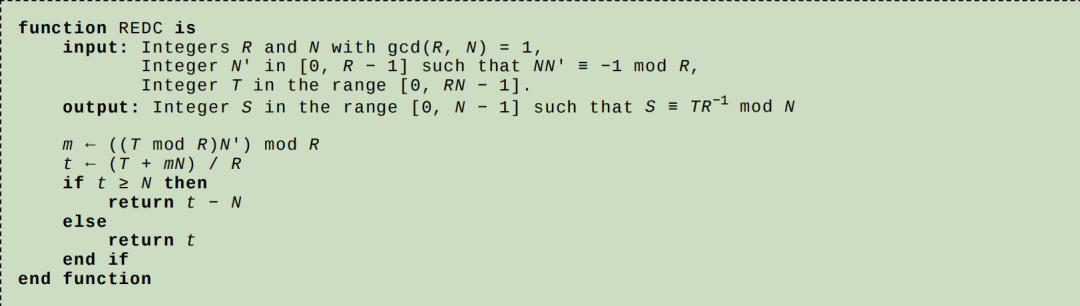
要验证这个算法的正确性，首先观察到 m 被选择得恰好使得 T + mN 可以被 R 整除。一个数可以被 R 整除当且仅当它对模 R 同余于零，我们有以下关系式：

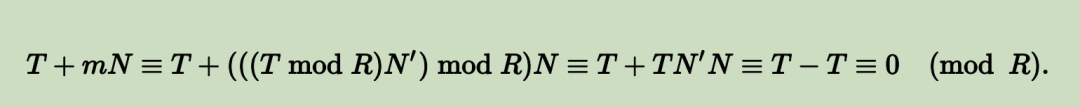
因此，t 是一个整数。其次，输出结果要么是 t，要么是 t - N，两者都与 t 对模 N 同余。因此，为了证明输出结果对模 N 同余于 $TR^{-1}$，只需证明 t 同余于 $TR^{-1}$。在模 N 下，t 满足以下关系式：

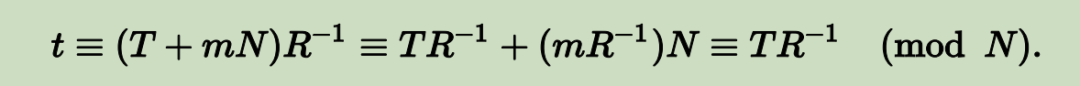
因此，输出结果具有正确的剩余类。第二，m 在 [0, R-1] 范围内，因此0 < T + mN < (RN - 1) + (R - 1)N 。因此，t 小于 2N，并且由于它是一个整数，所以 t 落在 [0, 2N - 1] 的范围内。因此，将 t 缩减到所需范围内最多需要一次减法运算，因此算法的输出落在正确的范围内。

使用REDC算法计算模17下的7和15的乘积，首先转换为蒙哥马利形式，并将其作为整数相乘得到12，如上所述, 使用R = 100，N = 17，N' = 47和T = 12来应用REDC算法。\ 第一步将m设置为12 ⋅ 47 mod 100 = 64。\ 第二步将t设置为(12 + 64 ⋅ 17) / 100。注意到12 + 64 ⋅ 17等于1100，正如预期的是100的倍数。t被设置为11，小于17，因此最终结果是11，与前面部分的计算一致。

作为另一个例子，考虑以R = 10, 计算7 ⋅ 15 mod 17的乘积。使用扩展欧几里得算法，计算出-5 ⋅ 10 + 3 ⋅ 17 = 1，因此N' = -3 mod 10 = 7。7和15的蒙哥马利形式分别为70 mod 17 = 2和150 mod 17 = 14。它们的乘积28是REDC的输入T，由于28 < RN = 170，满足REDC的假设条件。运行REDC，将m设置为(28 mod 10) ⋅ 7 mod 10 = 196 mod 10 = 6。然后计算28 + 6 ⋅ 17 = 130，因此t = 13。因为30 mod 17 = 13，这是3 = 7 ⋅ 15 mod 17的蒙哥马利形式。

Arithmetic in Montgomery form

在蒙哥马利形式下，许多与模 N 相关的操作同样适用。加法、减法、取反、相等比较、乘以一个不在蒙哥马利形式下的整数以及与 N 的最大公约数等操作都可以使用标准算法完成。雅可比符号可以计算为

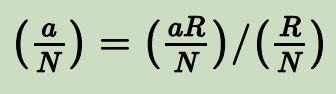
当 R > N 时，大多数其他算术操作可以用 REDC 表示。这个假设意味着两个模 N 的代表元的乘积小于 RN，这正是 REDC 生成正确输出所必需的准确假设。特别地，aR mod N 和 bR mod N 的乘积是 REDC((aR mod N)(bR mod N))。乘法和 REDC 的组合操作通常被称为蒙哥马利乘法。转换为蒙哥马利形式是通过计算 REDC((a mod N)( $R^2$ mod N)) 完成的。\ 从蒙哥马利形式转换出来是通过计算 REDC(aR mod N) 完成的。aR mod N 的模反元素是 REDC((aR mod N)$^{-1}(R^3$ mod N))。模幂运算可以使用平方法进行，将初始乘积初始化为 1 的蒙哥马利表示，即 R mod N，并将乘法和平方步骤替换为蒙哥马利乘法。

Montgomery arithmetic on multiprecision integers 多精度

大多数密码学应用需要数位数达到几百甚至几千位。这样的数值太大，无法存储在单个机器字word中。通常，硬件执行的是对某个基数 B 取模的乘法，因此进行更大的乘法运算需要组合多个小乘法。基数 B 通常为 2，REDC 算法要求对模 R 的乘积进行计算，通常 R > N，以便使用 REDC 计算乘积。然而，当 R 是 B 的幂时，有一种 REDC 变体只需要对机器字大小的整数进行乘积计算。假设正的多精度整数以小端方式存储，即 x 存储为数组 x[0]，...，x[ℓ - 1]，满足对于所有 i，0 ≤ x[i] < B，且 x = ∑ x[i] Bi。算法从一个多精度整数 T 开始，并一次一个字进行约简。首先，添加适当的 N 的倍数，使得 T 可被 B 整除。然后，添加 N 的倍数，使得 T 可被 B^2 整除，依此类推。最终，T 可被 R 整除，在除以 R 后，算法与 REDC 在计算 t 后处于相同位置。

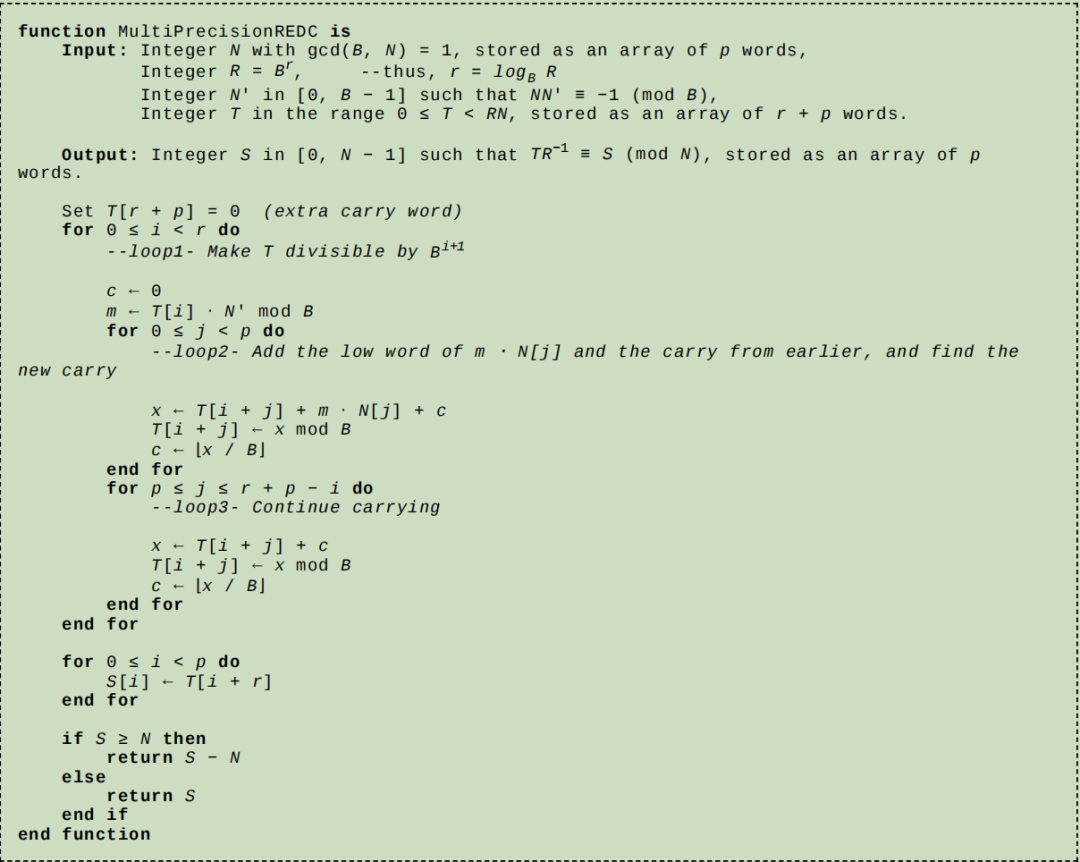
最后的比较和减法是通过标准算法完成的。上述算法之所以正确，基本上和 REDC 算法的正确性原因相同。每次进入 i 循环时，选择 m 使得 T[i] + mN[0] 可被 B 整除。然后将 mNBi 添加到 T 中。 由于这个量在模 N 下等于零，添加它不会影响 T 对模 N 的值。如果 mi 表示在循环的第 i 次迭代中计算的 m 的值，则该算法将 S 设置为 T + (∑ mi Bi)N。由于 MultiPrecisionREDC 和 REDC 产生相同的输出，这个和就等于 REDC 算法会选择的 m。T 的最后一个字，T[r + p]（因此 S[p]），仅用于存储进位，因为初始约简结果将限制在 0 ≤ S < 2N 的范围内。因此，如果预先知道 R ≥ 2N，可以完全避免这个额外的进位字。在典型的二进制实现中，这等价于说如果 N 的位数小于 R 的位数，则可以避免该进位字。否则，进位将为零或一。根据处理器的不同，可以将这个字存储为进位标志位，而不是一个完整的字。

可以将多精度乘法和 REDC 结合为一个单独的算法。这个组合算法通常被称为蒙哥马利乘法。具体实现有成熟算法库可以使用，不再赘述。

小结

本文主要基于维基百科内容，做了修改和阐述，其中蒙哥马利形式体现了数学中常用的映射的思想。一个代数集合上不容易处理的问题， 通过同态（同构）两手段，映射到另一个集合上，后者处理完成，才反射回去， 看似曲线救国，实则加速救国！！

参考：https://en.wikipedia.org/wiki/Montgomery_modular_multiplication

感谢关注， 欢迎讨论！！！

本文首发于：https://mp.weixin.qq.com/s/fDSbugVHzRNJPcsy4JGtDg