安全可靠 - 深入了解 STARK 安全系统

原文：Safe and Sound – A Deep Dive into STARK Security

译者：W3.Hitchhiker

STARK 完整安全性的深度分析

TL;DR

• 非交互式 STARK 来源于交互式预言机证明 (IOP) ，并在随机预言机模型中编译成非交互式证明。
• 这篇文章解释了 ethSTARK 文档的最新更新，其中对随机预言机模型中 ethSTARK 协议的安全性进行了全面而具体的分析。

STARK 安全性详解

STARK 证明系统（可扩展的透明知识论证）是一个强大的计算完整性工具：它允许以一种无信任的方式验证在公共数据上执行的计算的正确性。在这篇文章中，我们将深入探讨 STARK 证明所提供的安全性，对其进行定义，并探索证明方案安全性的技术。

(详情请阅读 ethSTARK 文档（1.2 版）第 6 节，以及 Block 等人就此主题所做的重要而全面的独立工作）。

我们的安全分析要达到什么目的？我们希望防止对 STARK 系统的"成功攻击"，这种攻击是由虚假陈述和 STARK 验证者接受的针对该（虚假）陈述的 STARK 证明引起的。由于虚假陈述是很危险的，而且它们可能以各种规模和形式出现，因此我们希望能够安全地防范所有虚假陈述。任何虚假陈述，即使是微不足道的 1+1=3，只要与 STARK 验证者接受的 STARK 证明相结合，就会被视为对系统的成功攻击。(有密码学背景的人可能有兴趣知道，STARK 还满足更强的安全概念，如知识可靠性，但为了简单起见，这篇文章将重点讨论更简单的可靠性）。

我们如何正式定义 STARK 系统的安全性？我们通过分析"可靠性误差"来实现。"卡考性误差"大致衡量了攻击者构建一次成功攻击所需的预期"成本"（即为一个虚假陈述找到一个 STARK 证明，但该虚假陈述仍被 STARK 验证者接受）。从数学上讲，可靠性误差是一个函数 e(t)，它的输入是时间参数"t"，代表攻击者为发起攻击所愿意花费的计算时间，输出则是攻击者攻击成功的概率（为虚假陈述找到令人信服的证明）。随着攻击者愿意花费的"成本" t 的增加，其成功概率也会增加。

到目前为止，我们已经将 STARKs 的安全性定义为一个函数 e(t)，这与你们在加密推特上讨论安全性的方式不同。在推特上，你可能会听到这样的说法："该方案有 96 比特的安全性"。这种说法如何转化为我们对安全的定义？对此没有统一的答案，因为人们对"x 比特安全性"的理解略有不同：

严格解释的话，对于在 1 和 2⁹⁶之间的任何 t，可靠性误差为 e(t) ≤ 2⁹⁶。这意味着任何运行时间不超过 2⁹⁶的攻击者成功的概率很小，小于 1/2⁹⁶，即小于十亿分之一乘以十亿分之一。

一种更宽松、或许也更常见的解释是，96 比特的安全性意味着对于任意 t都有，t/e(t) ≥ 2⁹⁶的情况。这意味着成功概率与运行时间成（反）线性关系。例如，如果攻击者的运行时间为 2⁸⁶，则其成功概率最多为 1/2 ¹⁰。

在本文中，我们将讨论第二种方案。

从 IOP 到具有 96 比特安全性的 STARK

那么，我们如何证明一个方案具有 96 比特的安全性呢？要回答这个问题，我们需要了解 STARK 的高层结构。STARK 由三个主要部分组成：IOP（交互式预言机证明）、默克尔树和 Fiat-Shamir 哈希；我们将重点讨论的部分是 IOP。一旦指定了这些组件，我们就可以将它们编译成 STARK。以下，我们将详细介绍这些组件、它们是什么以及如何将它们组合在一起。

我们要审查的第一个组件是 IOP：IOP 类似于标准的交互式证明，即证明者和验证者进行多轮交互（我们仅限于公共币协议，即验证者只向证明者发送随机挑战）。在 IOP 中，验证者不会完全读取证明者的信息，而是从每条证明者信息中抽取少量比特。这就是后来编译的 STARK 的简洁性所在。

有了 IOP，如何从中构建 STARK？证明者的信息可能很长（实际上，它们比计算本身还要长）。为了压缩信息，我们使用默克尔树。默克尔树是一棵二进制哈希树，其中每个叶节点代表 IOP 中的一个查询或一个答案。树根是整个信息的承诺。当验证者想要读取信息中的特定位置时，证明者会提供该位置的值和验证路径。验证者就可以使用该路径来验证该值是否正确。IOP 验证者只从证明者信息中读取少量位置信息。因此，使用默克尔树可以实现简洁的协议（通信量小）。

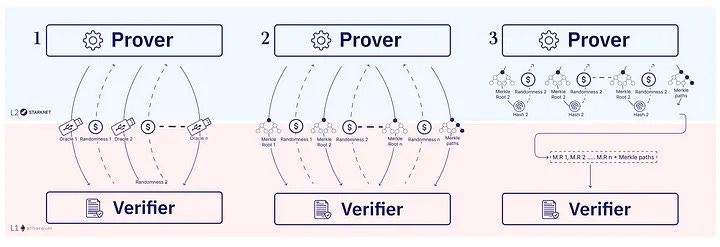
压缩轮次

我们可以选择交互式 STARK，但为了简化生成 STARK 的过程，我们通常会选择非交互式 STARK，这样验证者在构建 STARK 时就无需等待外部信息。事实上，这是目前所有 STARK 系统的部署方式，也是 ethSTARK 协议的构造方式。非交互式 STARK 也是透明 SNARK 的一种特例（透明意味着无需可信设置即可实例化；这也被称为 "Arthur Merlin 协议 "或"公共硬币 IOP"）。为此，最后一步是应用 Fiat-Shamir 算法将各轮压缩为一条信息，我们称之为 STARK 证明。Fiat-Shamir 转换是将交互式协议转换为非交互式协议的方法。验证者在"与哈希函数对话"时模拟交互式协议。为了得出第 i 轮的随机挑战，验证者对第 i 轮之前的部分副本进行散列，并将输出解释为下一个挑战。

这就确保了验证者在挑战生成后无法更改自己的回答。然而，作弊验证者有了一些新的策略途径，这是交互式 IOP 所没有的。验证者可以通过修改最后一条验证者信息来重新生成验证者的挑战，这样就会有新的记录，从而产生新的挑战。事实证明，IOP 的标准可靠性概念不足以证明 Fiat-Shamir 转换的安全性。

例如，一个有 96 轮的 IOP，并向验证者添加如下"hack"：如果验证者随机性的第一比特在 96 轮中每一轮都是 0，那么验证者就会接受（无需查看任何证明）。我们可以看到，在验证者中加入这一 hack 技术只会给 IOP 的可靠性误差增加 1/2⁹⁶ 的项。然而，经过 Fiat-Shamir 转换后，攻击者可以轻松修改验证者信息，确保每个哈希值都以 0 开头，从而在很短的时间内破解系统。请放心，这种可怕的情况只是一个理论上的例子，并不适用于已部署的 STARK。那么，让我们来看看为什么我们的 STARKs 始终是安全的？简而言之，我们将证明攻击者最多运行 t 步，攻击成功的概率为 e(t) ≤ t / 2⁹⁶。详情如下。

IOP 和逐轮可靠性

STARK 的安全性取决于其底层 IOP。但是，一个 IOP 具有 96 比特的安全性意味着什么呢？按照标准定义，IOP 的可靠性误差为 1/2⁹⁶：这意味着任何攻击者（无论运行时间长短）骗过验证者的概率最多为 1/2⁹⁶。然而，正如我们所讨论的，IOP 可靠性只是三个部分中的一个，这不足以让从所有三个步骤中编译出来的 STARK 获得 96 比特的安全性。取而代之的是，假设 STARK 有 96 比特逐轮可靠性误差（有时也使用一个被称为状态恢复可靠性的类似定义），那么编译后的 STARK 的安全性就得到了证明。

直观地说，逐轮可靠性是指每一轮都有 96 比特的安全性，而不仅仅是整个协议。更详细地说，逐轮可靠性是指存在一个谓词，它能获取协议的部分记录，并告诉我们这个记录是否是"欺骗性的"： “空记录”不是"欺骗性的"，而完整记录则是"欺骗性的"，当且仅当验证者接受它时。最后，对于任何不是"欺骗"验证者的部分文字记录，在下一轮中该文字记录变成"欺骗性的"的概率最多为 1/2⁹⁶。如果存在这样一个具有这些特性的谓词，我们就说该协议具有 96 比特逐轮可靠性（该谓词不要求可有效计算）。

在许多情况下，只分析 IOP 的可靠性，而不分析其逐轮可靠性。诚然，我们很难想到 IOP 具有标准可靠性而不具有逐轮可靠性的例子（人为制造的例子除外）。不过，在推导具体的安全边界时，两者之间的差异可能会出现，因为每个比特都很重要。因此，要推导出严密而具体的边界，就必须对 IOP 的逐轮可靠性进行严密分析。这正是我们对 FRI 协议和作为 STARKs IOP 基础的 ethSTARK IOP 所做的工作。分析本身远非小事，也超出了本篇文章的范围。利用新的分析方法，我们可以为我们的证明设置精确的参数。

逐轮可靠性确实为我们提供了所需的保证。证明者可以多次重新生成挑战，但我们知道，在任何一轮中，生成 "欺骗性"记录的概率都是 1/2⁹⁶。因此，如果验证者的时间为 t（以哈希调用次数来衡量），那么它最多可以尝试 t 次来获得 "欺骗性的"文本，这就将其成功概率限制

e(t) ≤ min{t /2⁹⁶,1} 。

添加所有错误项

最后，要使所有这一切成立，我们需要确保验证者无法篡改默克尔树。我们可以证明，只要证明者在哈希函数中没有发现碰撞，它就无法在默克尔树中作弊。攻击者使用 t 次调用（随机哈希函数）找到碰撞的概率至多为 min{t²/2ˢ,1}，其中 s 是哈希函数的输出长度（这是"生日悖论"造成的）。这就是为什么我们要设置哈希函数的长度为所需安全性的两倍。因此，如果我们有一个输出长度为 192 比特的哈希函数和一个逐轮可靠性为 96 比特的 IOP，我们就能得到一个编译后的 STARK，其稳健性误差为 e(t) = t /2⁹⁶ + min * {t² / 2¹⁹²,1}.。特别是，由于我们用来定义安全性的函数 t/e(t)满足不等式 t/e(t) ≥ t/(t /2⁹⁶ + min{t² / 2¹⁹²,1}), 而这个不等式的右边在 t=2⁹⁶ 时达到最小值，对于这个 t 值，我们有 t/e(t) ≥ 2⁹⁵，因此这种方案拥有 95 比特的安全性。

总结

总之，STARK 提供了一种功能强大的方法，可用于以无信任的方式验证在公共数据上执行的计算的正确性。STARK 的安全性通常用"可靠性误差"来衡量，它表示攻击者成功提供虚假陈述并用证明说服验证者的概率。要达到理想的安全等级（如 96 比特），底层 IOP 必须满足逐轮可靠性，确保每一轮都能保持较高的安全等级。我们分析了 SATRK 所依据的 IOP 的逐轮可靠性，从而得出了具体的安全界限。

-- 声明：本文内容仅供参考、交流，不构成任何投资建议。若存在明显的理解或数据的错误，欢迎反馈。

本文内容系 W3.Hitchhiker 原创，如需转载请标明出处。

商务合作：rex@w3hitchhiker.com

官网：https://w3hitchhiker.com/

W3.Hitchhiker 官方推特：https://twitter.com/HitchhikerW3