Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分

本文翻译自https://medium.com/@med456789d/uniswap-insights-part-2-of-6-568632aa4d8，原系列标题为 Uniswap v3 Math Insights ，共有六部分，此为第二部分。

为了让更多人可以访问和了解关于 Uniswap V3 投资的有用信息，我们翻译了系列文章，让中文读者对 Uniswap V3 机制和投资策略选择有更深入的理解。在阅读本翻译同时，可以随时参考原文以获取更多详细信息。

在第 1 部分中，我们着眼于寻找资金效率的边界。在本文中，我们将探讨当我们对价格持乐观或悲观态度时的边界。最后，我们将通过构建多个流动性提供（LP）位置来确定优化收益的方法，并借助 desmos 的帮助。

简而言之：

1. 通过倾向性的资本效率边界来选择一个价格范围的 方向性偏差 。

2. 将 LP 范围切分成 多个 LP 仓位，形成一个直方图 。

3. 节省燃气费用。将 LP 仓位一个放在另一个上面，而不是排成一排，以减少 LP 仓位的数量。

4. 使用 desmos 来将 LP 仓位与您自己的分布相匹配。

1. 选择方向性偏差

回想一下，在第 1 部分，我们通过将 LP 范围设置为 +/-84% 来解决了在平衡资本效率的同时最大化 LP 范围的方法。但是，84％ 边界方法不旨在优化收益，且并不适用于当投资者预测到流动池的代币将可能价格上涨的情况（因为 +/-84% 是对称的）。让我们通过简单地添加参数 “a” 来调整我们的边界，以适应价格方向性偏差（此处，参数 “a” 位于价格的上界分母与下界分子是一样的效果）。

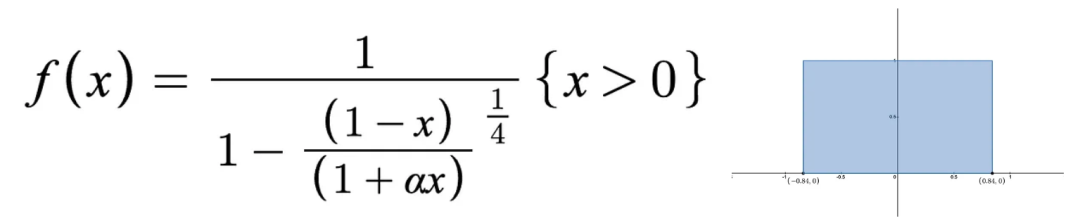参数 alpha 允许我们偏斜我们的 LP 仓位的效率边界

为了看到之前提到的原始 84％边界，我们设置 a=1，即上图蓝色的部分。如果我们认为收益将上升两倍而不是下降，我们将 a=2。请参见下面 a=[0…3]的可视化效果。

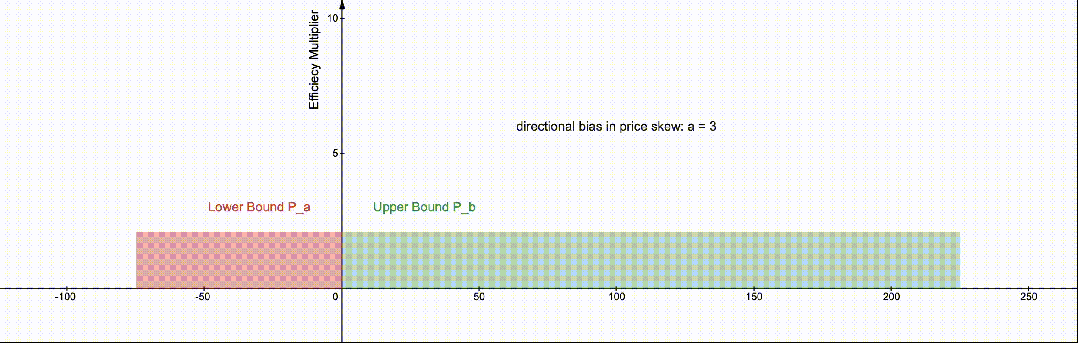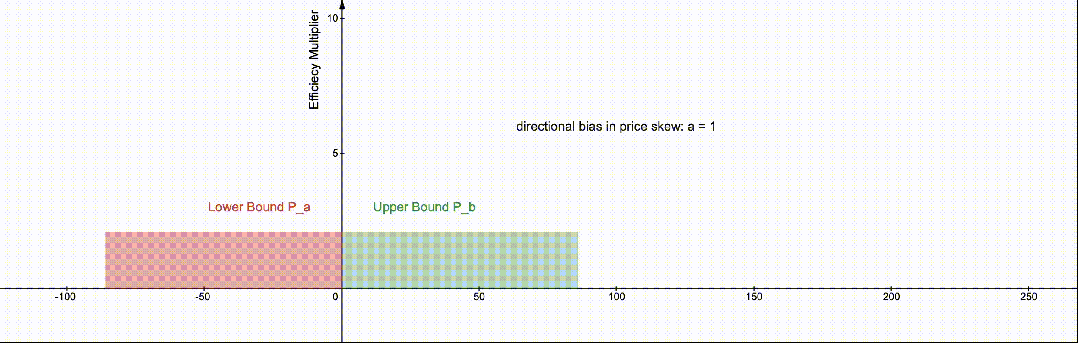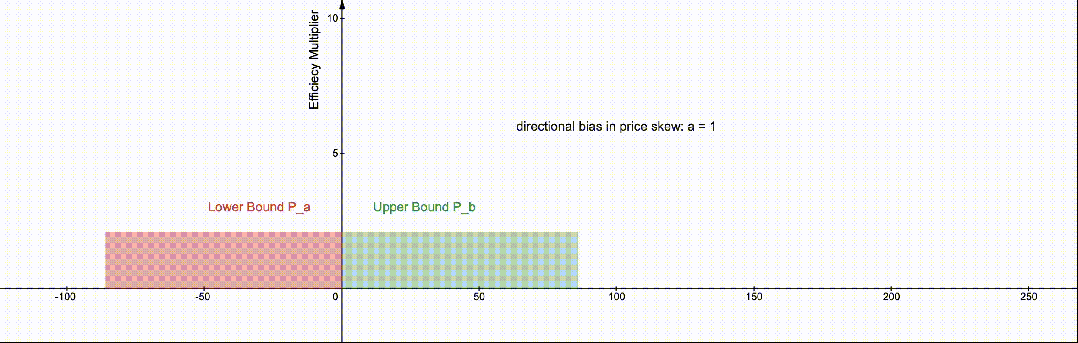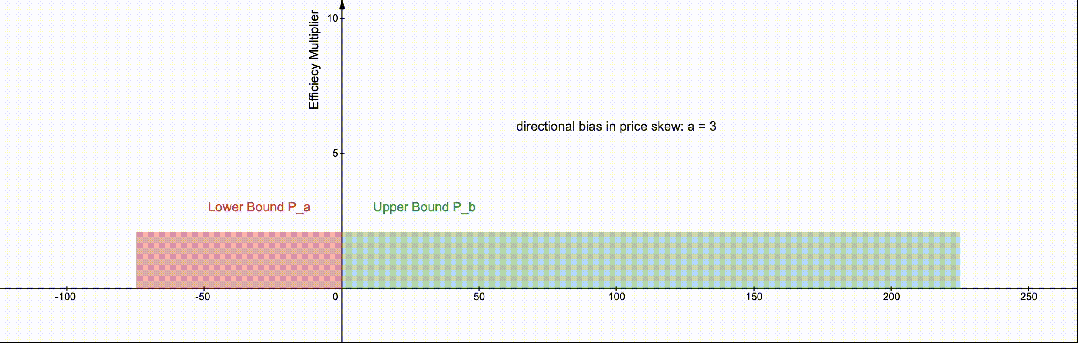随着我们对价格的方向性观点的提高，我们的 LP 位置的最佳效率边界的百分比也会发生变化。

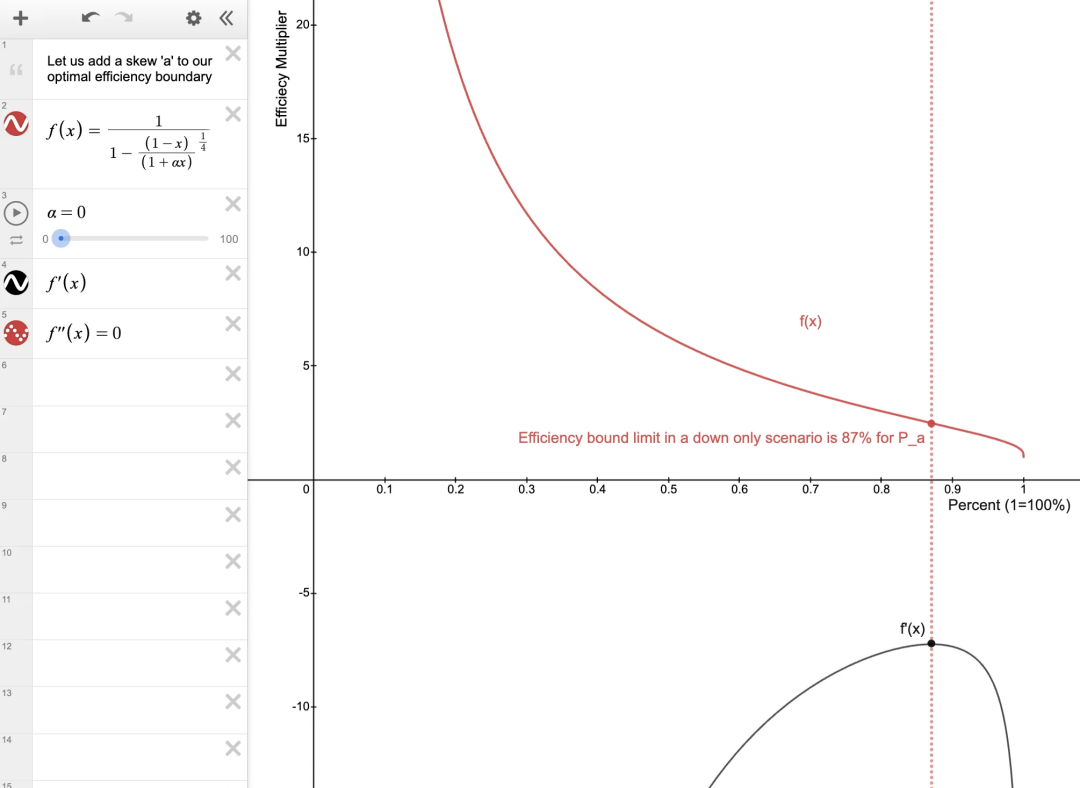
如果我们认为价格只会下跌，我们可以将 a 设置为 0，甚至可以发现 87％的下限价格成为资本效率的最大边界。提供当前价格比率之外的流动性效率较低。

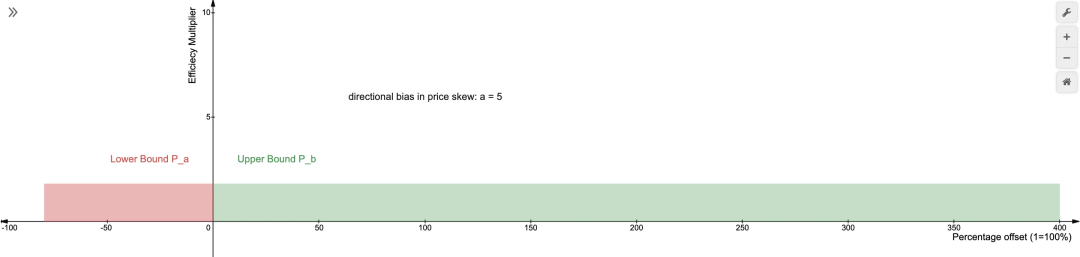
当我们将偏差增加到 5 时，我们的最佳峰值会向下移动到较低边界的 80％，而上边界则会向上移动至 5x80％ = 400％。

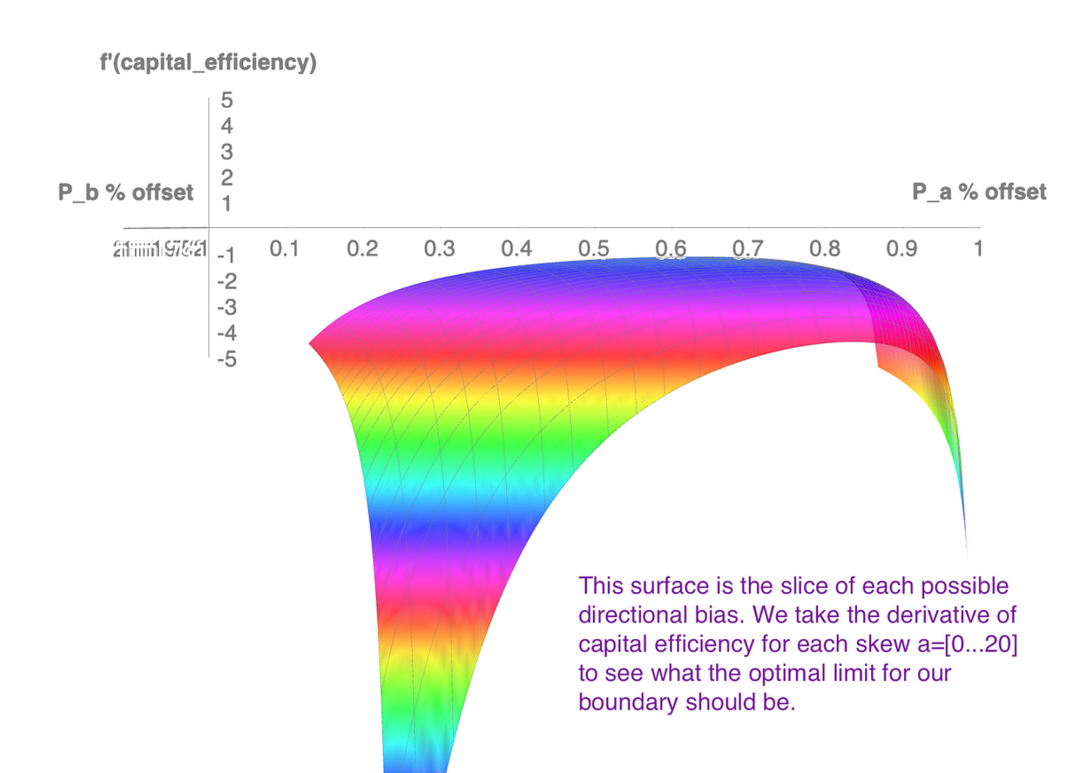
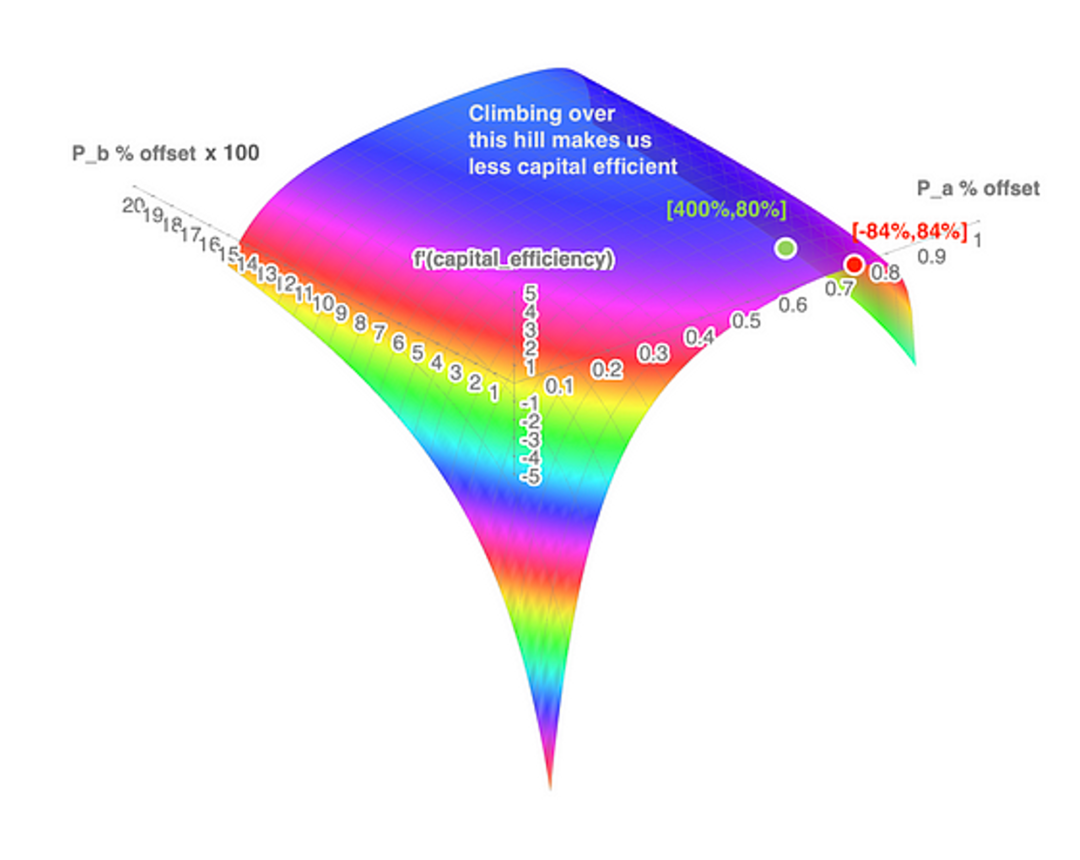
在二维平面上可视化每种可能方向偏差的边界非常困难，但是如果我们为资本效率的导数创建第三个轴，我们可以看到它在三维中的峰值位置（我们将参数 a 算入头寸范围的上下边界，并且将其作为平面的 x、y 轴，资本效率的导数作为 z 轴）。

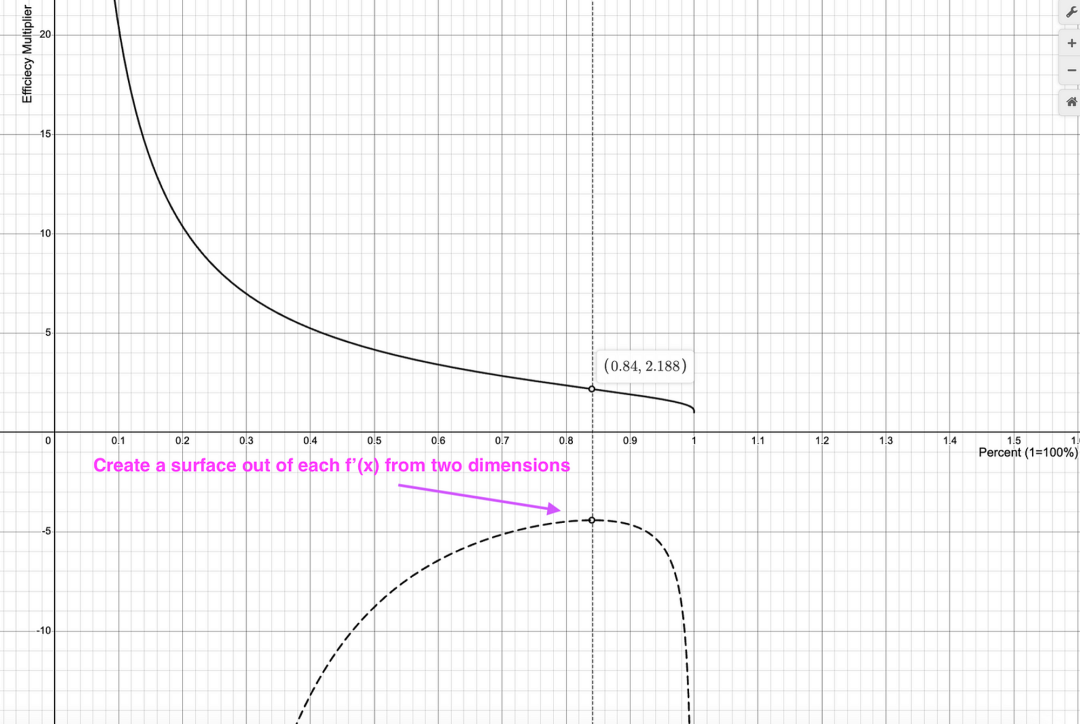
我们也可以在红点和绿点上找到 +/-84％ 和 -80％/ + 400％ 。
f’(capital_efficiency)的交互式3D表面：https://www.math3d.org/dxHSLpaZZ

主要观点是，将下限 p_a 设置为低于 87％ 会略微低效。对于乐观主义者而言，重要的是，下限（p_b）并不那么敏感于偏差。在偏差为 10（您认为每 1％ 下跌价格可能上涨 10％）的情况下，仍然有 77％ 的下限。

根据我们对价格可能变动的乐观程度或悲观程度， 我们可以使用 Desmos 工具来调整我们的效率边界： https://www.desmos.com/calculator/0l7i8kmukx 。 在偏斜范围之外提供流动性会减少资本的有效利用。

寻找边界的另一种方法

请注意，也可以根据选择投入到池中的资本量的少多来解决最大范围的问题。 我们可以反向解决资本效率问题。 例如，如果一个人有 100 美元的投资组合，他可能只想冒险投入 20 美元的资本，将其余 80 美元存入收益固定的国债中。资本效率目标 “E” 变为 20 = 5。考虑到偏差 a=2，边界应该是多少？

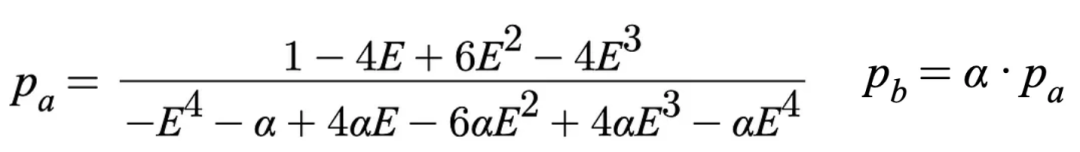可以通过已知 y（资本效率）来解决查找价格边界的方程式中的 x

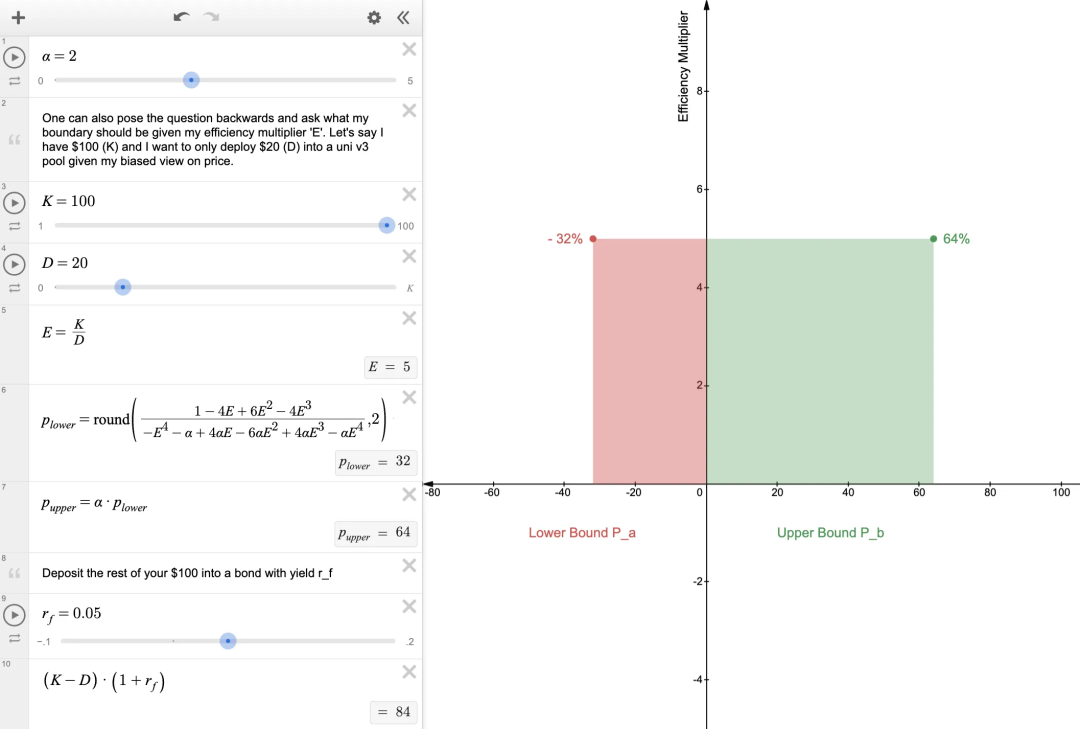当资本效率为5，我们得到从先前的例子中的 -32％ 和 +64％

我也提供了一个可用于计算效率边界的工具：https://www.desmos.com/calculator/a8kt8g6kia

无论使用哪种方法来查找边界，现在可以在这些边界内工作以进一步优化。

好了，我们该如何做？现在来到有趣的部分。我们要切割我们的 LP 位置！

“我们要切割LP位置”-Jerry Seinfeld-

2. 将范围切成多个 LP 位置

第 1 部分分说到，随着时间的推移，价格有扩散的趋势。这意味着，价格比率随时间的变化并不符合矩形做市范围的形状。也就是说，价格分布在入场价格周围扩散，就像这样：

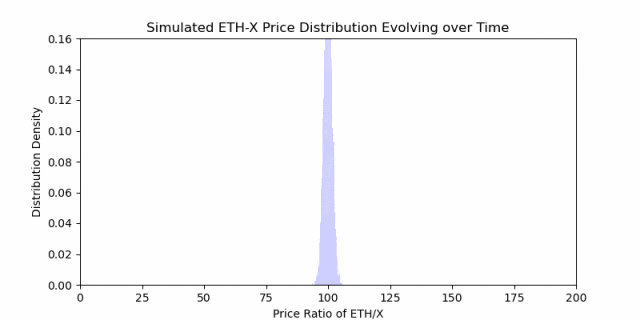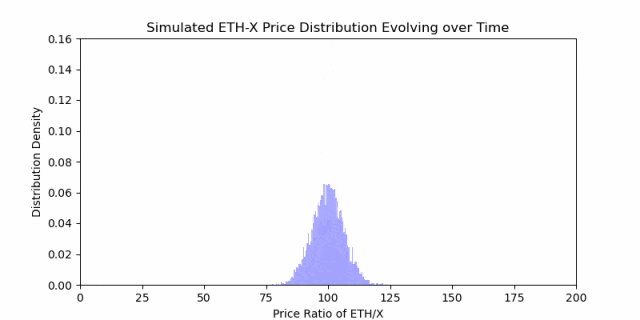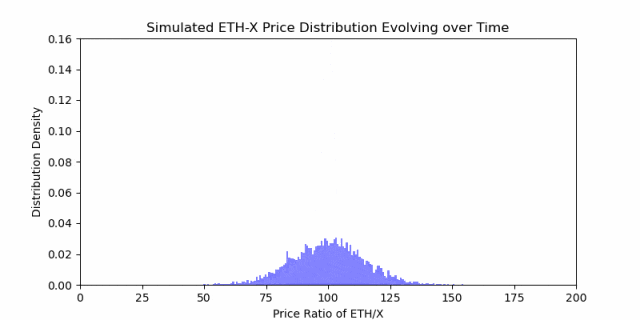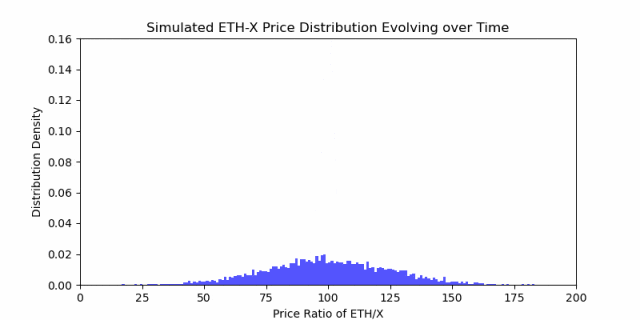价格变动可以看作一个随机过程，其随着时间的推移最终会分散开来。单个矩形不是捕获收益的最佳选择。

随着我们远离起始价格，我们需要调整矩形形状。最简单的方法是将矩形 LP 范围分成多个范围，并使它们适合于分布内部。LP 位置将是效率边界内的积分。

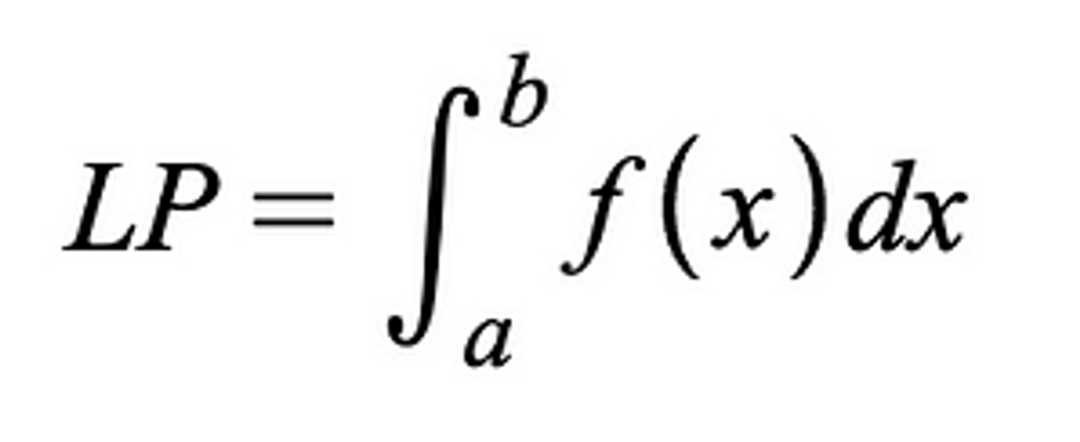我们使用 Riemann 积分将下限价格和上限价格之间的区域相加，而 Desmos 则为我们完成所有计算

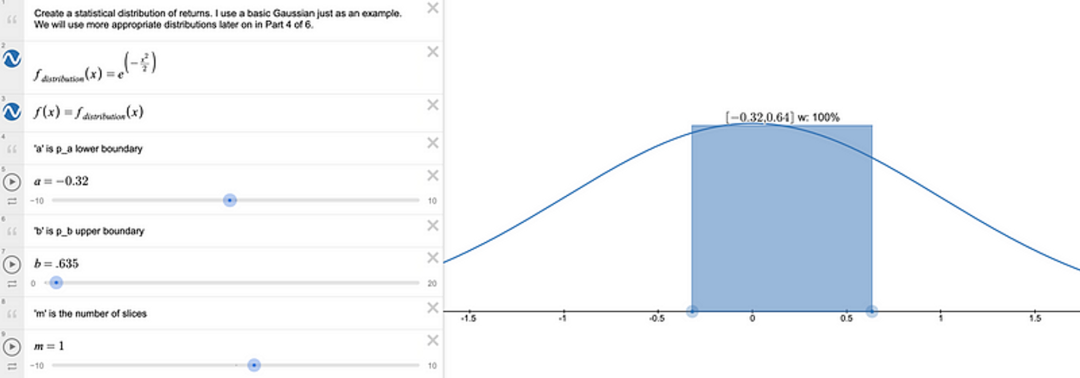我们使用之前示例中的 -32% 和 +64%，资本效率设定为 5，偏斜度设定为 2

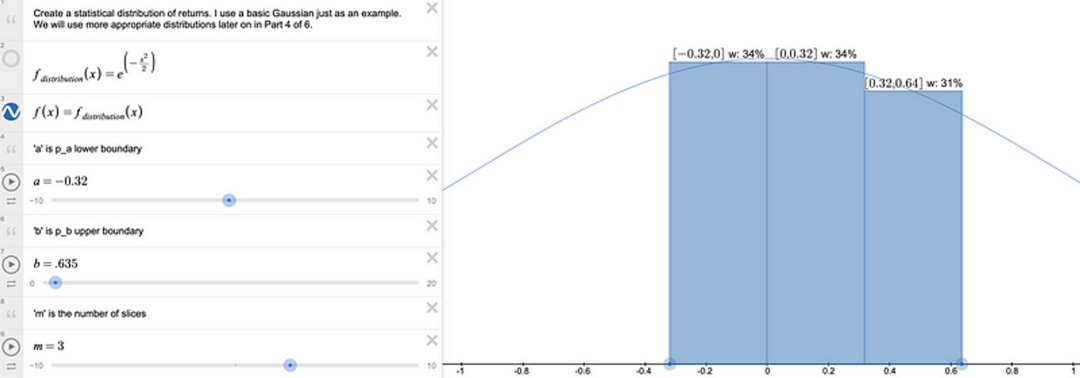可以使用交互式工具，链接在这里：https://www.desmos.com/calculator/nab8lx6cbi。高斯分布不应被用于处理异常值，我们将在将来讨论更合适的分布。

注意我们是如何创建了三个 LP 仓位，并赋予它们三个权重的。一个 LP 仓位会根据在 desmos 链接中定义的范围和权重来分配资金。但是，这种方法可以通过垂直切片（使用 Lebesgue 积分方法而不是 Riemann）来改进。

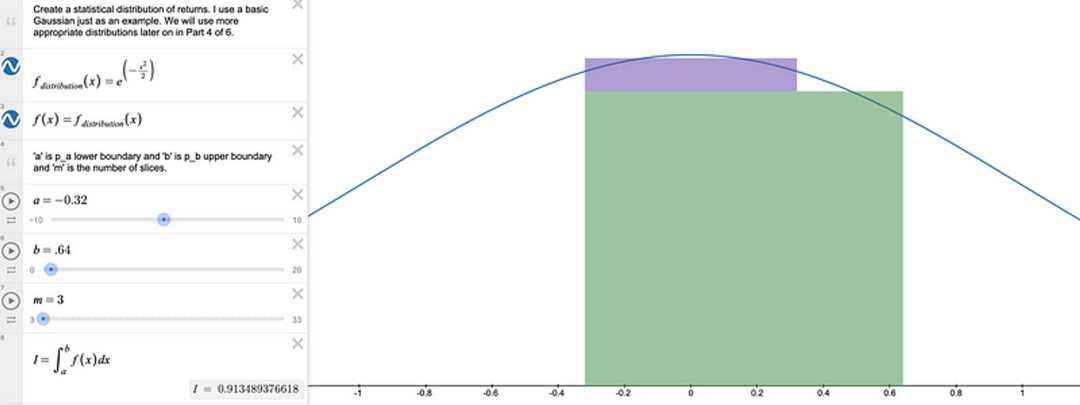Lebesgue 方法并不那么简单，但可以减少燃气费用和 LP 仓位的数量。我们将在第 6 部分详细讨论应该将 LP 仓位切片多少次

请注意，高斯分布只是一个基本的示例分布，不代表实际世界中的某些分布。您可以尝试将更复杂的分布插入到 f(x) 中。但请注意，实际世界与示例有所不同：

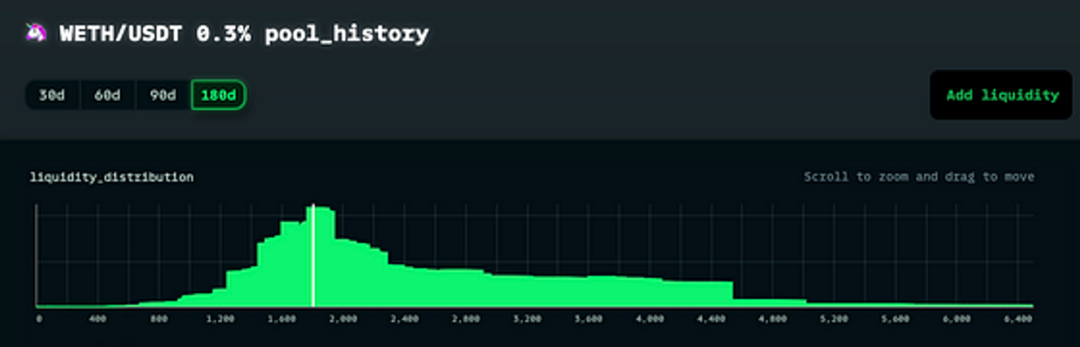
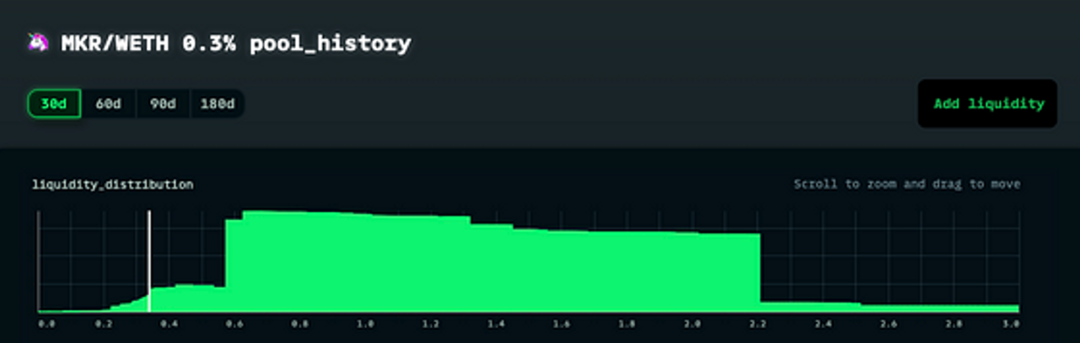MKR/ETH 请注意偏斜，我们需要使用不对称方法来捕捉这种偏斜

为了捕捉这些高级分布，我们需要了解更多关于流动性指纹并将在第 3 部分中继续使用不对称的对数 Laplace 分布。

• 如果您觉得这个内容有教育意义，请随时关注这只刺猬的 Twitter 账号：@CK_2049

  免责声明：请注意，为了努力弥合中英文信息差，这篇文章从 Medium 上翻译而来，详细的英文原文请查阅以下链接。我们也欢迎您关注我们的账号 zelos-research。
  本研究仅供一般信息目的。Uniswap 基金会很慷慨地赞助了这次私人研究的出版。它不构成投资建议或买卖任何投资的建议或招揽，并且不应用于评估做出任何投资决策的优点。不应依赖它作为会计、法律或税务建议或投资建议。本文反映了作者当前的观点。这些意见可能会随时更改而不进行更新。

相关链接

原文链接：https://medium.com/@med456789d/uniswap-insights-part-2-of-6-568632aa4d8
关注 zelos-research：https://medium.com/zelos-research
我们的 github 仓库：https://github.com/orgs/zelos-alpha/repositories

推荐阅读

Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分
Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分