Plonky2 = Plonk + FRI

Plonky2由Polygon Zero团队开发，实现了一种快速的递归SNARK，据其团队公开的基准测试，2020年，以太坊第一笔递归证明需要60s生成，而于今Plonky2在 MacBook Pro上生成只需 170 毫秒。

下面将逐步剖析Plonky2。

1. 整体构造

每个零知识证明系统都由两部分构成。第一个是编写算术电路，第二个是多项式承诺方案。

Plonk2第一部分采用Plonk + custom gates (TurboPlonk)，第二部分没有选择KZG等典型的SNARK承诺方案，而是使用FRI承诺，一种与STARK相关的承诺方案。之所以选择FRI是因为：

• FRI不需要椭圆曲线，也就没有non-native arithmetic

• 可以使用Small Field

• 没有Trusted Setup

• 抗量子

此外在证明生成方面，FRI还提供一个别具趣味的选择：通过减少FRI rate、增加查询次数，可以快速生成证明，但生成的证明非常大，相反，通过增加FRI rate、减少查询次数，生成证明相对较慢，但生成的证明非常小。

2. Goldilocks Filed

   $P = 2 ^{64} - 2^{32} +1$

Plonky2使用Goldilocks Filed，很明显，这个域足够小，只有64位，可以直接用无符号64-bit表示，则这个域可以在CPU上进行非常高效的算术运算，如

• 将128位数取模p的操作非常廉价，如对应乘法操作，设x,y都是64bit，则 $x \cdot y$ 是128bit，

  具体实现代码见reduce_128

• 32bit的MulAdd操作不会溢出，如x,y,z都是32bit，$x \cdot y + z$ 不会溢出

单就域而言，使用64位的Goldilocks域比使用256位的KZG Commitment快40倍。

3. Starky

Starky与Plonk2具有相同的域哈希函数，但是没有计算比较重的算术，所以编写ZKVM使用Starky而不是Plonk2，Plonk2主要用于生成递归证明，因此Starky与Plonk2各自具有其独特的优势，可相互补充，具体来说，Starky为每个交易并行生成证明，然后交付Plonk2递归生成证明。

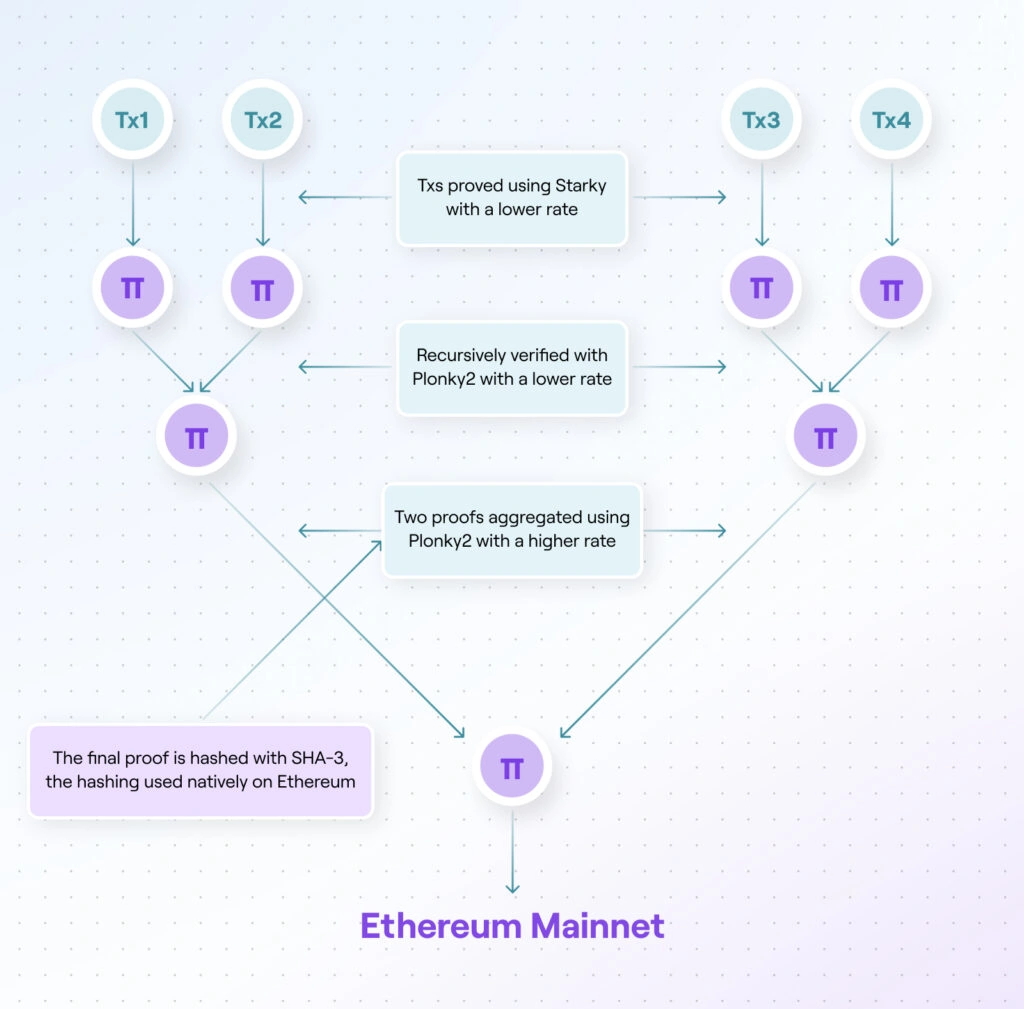
在上图递归的中间层，我们目标是快速生成证明，而不需要担心proof的大小，在最后一层，也就是生成根proof的那一层，这个proof 需要发送到L1层，如果proof很大，gas费势必很高，所以最后一层使用Plonk2 with a higher rate，中间层使用Plonk2 with a lower rate。