uniswap v2

恒定乘积 x * y = k

无手续费计算

用x兑换y，求用Δx能兑换多少y x y = k = (x + Δx) (y - Δy)

(y - Δy) = $\frac{x * y}{x + Δx}$

Δy = y - $\frac{x * y}{x + Δx}$

Δy = y * ( 1 - $\frac{x}{x + Δx}$)

Δy = y * ($\frac{x + Δx - x}{x + Δx}$)

Δy = y * ($\frac{Δx}{x + Δx}$)

用x兑换y，想要Δy 需要多少x x y = k = (x + Δx) (y - Δy)

x + Δx = $\frac{x * y}{y - Δy}$

Δx = $\frac{x * y}{y - Δy}$ - x

Δx = x * ($\frac{y}{y - Δy}$ - 1)

Δx = x * $\frac{y - (y - Δy)}{y - Δy}$

Δx = x * $\frac{Δy}{y - Δy}$

有手续费计算

用x兑换y，求用Δx能兑换多少y 其中千分之997的Δx能用于兑换, 剩下的千分之3存储到流动性池子中, 做为流动性提供奖励。设可用于兑换的系数叫做β x y = k = (x + Δxβ) * (y - Δy)

(y - Δy) = $\frac{x y}{x + Δxβ}$

Δy = y - $\frac{x y}{x + Δxβ}$

Δy = y ( 1 - $\frac{x}{x + Δxβ}$)

Δy = y ($\frac{x + Δxβ - x}{x + Δx*β}$)

Δy = y ($\frac{Δxβ}{x + Δx*β}$)

Δy = y ($\frac{Δx \frac{997}{1000} }{x + Δx * \frac{997}{1000} }$)

Δy = y ($\frac{Δx 997 }{1000 x + Δx 997 }$)

用x兑换y，想要Δy 需要多少x 同样的公式, 求Δx x y = k = (x + Δxβ) * (y - Δy)

x + Δxβ = $\frac{x y}{y - Δy}$

Δxβ = $\frac{x y}{y - Δy}$ - x

Δxβ = x ($\frac{y}{y - Δy}$ - 1)

Δxβ = x $\frac{y - (y - Δy)}{y - Δy}$

Δxβ = x $\frac{Δy}{y - Δy}$

Δx $\frac{997}{1000}$ = x $\frac{Δy}{y - Δy}$

Δx = x $\frac{Δy}{y - Δy}$ $\frac{1000}{997}$

Δx = x $\frac{Δy 1000}{(y - Δy)*997}$

提供流动性

首次次提供流动性 lp = $\sqrt{x * y} - 1000$

后续提供流动性 lp = min($(\frac{Δx}{x}lp)$ , $(\frac{Δy}{y}lp)$)

如果在首次添加流动性时不减1000会有导致什么问题 例如: 首次添加币对 1wei weth 和 1wei wbtc 计算出lp = 1wei (最小单位) 这时再向pair合约中转入1000个weth和10个wbtc，然后调用sync()同步数据 此时1wei流动性代表了1000个weth和10个wbtc

这时如果有其他用户想添加流动性，只能存入大于1000weth或10个wbtc(计算出来的lp不能比1wei再小了)。这样该币对的门槛就太高了,如果被用来攻击会导致整个协议无法使用。

如果在首次添加流动性时将1000个lp转移走，这时如果还想上面的攻击，存入1001 wei的x 和 1001 wei的y，然后再向pair合约中存入1000个weth和10个wbtc，这时只有$\frac{1001-1000}{1001}$的资产属于你，将损失$\frac{1000}{1001}$的资产。所以初次添加流动性时计算出来的lq越大，损失的lq越小 比如初次铸造1000000个lq损失的$\frac{1000}{1000000}$将忽略不计。

为什么要将lp转给address(0)而不是require(lp > 1000)呢 uniswap v2要解决的问题是强制初次添加的流动性产生的lp要足够多，这样才会给后面的用户机会去添加流动性。如果只是require lp > 1000判断，攻击者还是可以的达到上述攻击，比如存入1001 wei个x和1001 wei个y，然后存入1000000个weth和10000个wbtc，这样其他用户添加流动性时最小也要$\frac{1000000}{1000}$个weth，这样只是成本多了但是没有损失，因为这1000个lp都是他自己的。

交易滑点

当有多个交易并发成交时，导致当前价格不准确，会产生滑点。 比如交易前eth 100usdt/个，但本次交易前有其他交易用usdt兑换了10000个eth，导致池子中的eth价格提升至102usdt/个。本来打算用1000u兑换eth，能兑换10个eth，实际只兑换了9.8个。 在swap过程中会有amountOutMin参数来限制输出结果，防止滑点过大造成损失。 在uniswap-interface 计算滑点 calculateSlippageAmount test case如下:

// tokenAmount = 100, 200是万分之200，结果就是100±(100 * 2%)
expect(calculateSlippageAmount(tokenAmount, 200).map(bound => bound.toString())).toEqual(['98', '102'])

默认的滑点是50/10000

// default allowed slippage, in bips
export const INITIAL_ALLOWED_SLIPPAGE = 50

流动性代币质押

在uniswap v2中提供了质押lp token赚取收益的活动，目的也是为了让用户提供更持久的流动性。具体收益计算如下图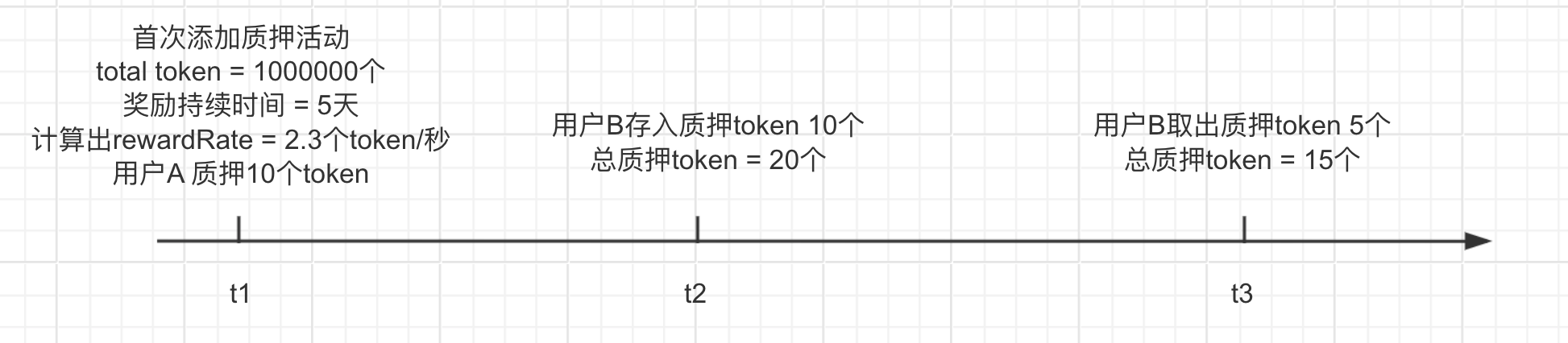： 创建活动时提供共1000000个奖励token，奖励时间5天，用户A已经向其中存入10个token。 t1：rewardRate = $\frac{1000000}{5 day seconds}$ = 2.3个token/秒 (回报率) t2：rewardPerTokenStored = 0 + $\frac{2.3 (t2 - t1)}{10}$ (t1-t2时间段内每个质押的token赚取的奖励) t3：新用户B质押10个token，总共20个token，rewardPerTokenStored = 0 + $\frac{2.3 (t2 - t1)}{10}$ + $\frac{2.3 (t3 - t2)}{20}$ 累计每个时段内每个token收益 t3：计算用户A的奖励 rewardA = 10 $\frac{2.3 (t2 - t1)}{10}$ + 10 $\frac{2.3 (t3 - t2)}{20}$ rewardA = 10 ($\frac{2.3 (t2 - t1)}{10}$ + $\frac{2.3 (t3 - t2)}{20}$) userRewardPerTokenPaid存储的是每次操作时当时的累计值： userRewardPerTokenPaid_current - userRewardPerTokenPaid₁ = $\frac{2.3 (t2 - t1)}{10}$ + $\frac{2.3 (t3 - t2)}{20}$